Skip to main content
SpringerLink
Log in

Stability analysis of a noise control system in a duct by using delay differential equation

  • Research Paper
  • Published:
Acta Mechanica Sinica Aims and scope Submit manuscript

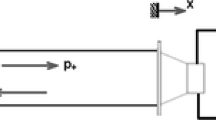
Abstract

The paper deals with the criteria for the closed-loop stability of a noise control system in a duct. To study the stability of the system, the model of delay differential equation is derived from the propagation of acoustic wave governed by a partial differential equation of hyperbolic type. Then, a simple feedback controller is designed, and its closed-loop stability is analyzed on the basis of the derived model of delay differential equation. The obtained criteria reveal the influence of the controller gain and the positions of a sensor and an actuator on the closed-loop stability. Finally, numerical simulations are presented to support the theoretical results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Fuller C.R., von Flotow A.H.: Active control of sound and vibration. IEEE Control. Syst. Mag. 15(6), 9–19 (1995)

    Article  Google Scholar 

  2. Kuo S.M., Morgan D.R.: Active noise control: a tutorial review. Proc. IEEE 87(6), 943–975 (1999)

    Article  Google Scholar 

  3. Wu Z., Varadan V.K., Varadan V.V., Lee K.Y.: A state-space modeling of one-dimensional active noise control systems. ASME J. Vib. Acoust. 117(2), 220–225 (1995)

    Article  Google Scholar 

  4. Wu Z., Varadan V.K., Varadan V.V.: Time-domain analysis and synthesis of active noise control systems in ducts. J. Acoust. Soc. Am. 101(3), 1502–1511 (1997)

    Article  Google Scholar 

  5. Hull A.J., Radcliffe C.J., Miklavcic M., MacCluer C.R.: State space representation of the nonself-adjoint acoustic duct system. ASME J. Vib. Acoust. 112(4), 483–488 (1990)

    Article  Google Scholar 

  6. Hull A.J., Radcliffe C.J., Southward S.C.: Global active noise control of a one-dimensional acoustic duct using a feedback controller. ASME J. Dyn. Syst. Meas. Control. 115(3), 488–494 (1993)

    Article  Google Scholar 

  7. Hong J.H., Akers J.C., Venugopal R., Lee M.N., Sparks A.G., Washabaugh P.D., Bernstein D.S.: Modeling, identification, and feedback control of noise in an acoustic duct. IEEE Trans. Control. Syst. Technol. 4(3), 283–291 (1996)

    Article  Google Scholar 

  8. Lin J.Y., Sheu H.Y., Chao S.C.: LQG/GA design of active noise controllers for a collocated acoustic duct system. J. Sound. Vib. 228(3), 629–650 (1999)

    Article  Google Scholar 

  9. Yang, Z.Y.: Design of active noise control using feedback control techniques for an acoustic duct system. In: IEEE Conference on Robotics, Automation and Mechatronics, pp. 467–472. Singapore (2004)

  10. Stépán G.: Retarded Dynamical Systems: Stability and Characteristic Functions. Longman Scientific & Technical, London (1989)

    MATH  Google Scholar 

  11. Hu H.Y., Wang Z.H.: Dynamics of Controlled Mechanical Systems with Delayed Feedback. Springer, New York (2002)

    MATH  Google Scholar 

  12. Kuang Y.: Delay Differential Equations with Applications in Population Dynamics. Academic Press, Dublin (1993)

    Book  MATH  Google Scholar 

  13. Niculescu S.I.: Delay Effects on Stability: a Robust Control Approach. Springer, New York (2001)

    MATH  Google Scholar 

  14. Diaz G., Sen M., Yang K.T.: Effect of delay in thermal systems with long ducts. Int. J. Therm. Sci. 43(3), 249–254 (2004)

    Article  Google Scholar 

  15. Banks H.T., Demetriou M.A., Smith R.C.: Robustness studies for H∞ feedback control in a structural acoustic model with periodic excitation. Int. J. Robust. Nonlinear. Control 6(5), 453–478 (1996)

    Article  MATH  MathSciNet  Google Scholar 

  16. Avalos G., Lasiecka I., Rebarber R.: Lack of time-delay robustness for stabilization of a structural acoustics model. SIAM J. Control. Optim. 37(5), 1394–1418 (1999)

    Article  MATH  MathSciNet  Google Scholar 

  17. Boonen, R., Sas, P.: Stability improvement for feedback noise control in ducts using a time delay compensator. In: Proceedings of the 25th International Conference on Noise and Vibration Engineering, ISMA, pp. 31–36. Leuven, Belgium (2000)

  18. Bitsadze A.V., Kalinichenko D.F.: A Collection of Problems on the Equations of Mathematical Physics. Mir, Moscow (1980)

    Google Scholar 

  19. McOwen R.C.: Partial Differential Equations: Methods and Applications. Prentice Hall, New Jersey (1996)

    MATH  Google Scholar 

  20. Morris K.: Noise reduction in ducts achievable by point control. ASME J. Dyn. Syst. Meas. Control 120(2), 216–223 (1998)

    Article  Google Scholar 

  21. Seto W.W.: Theory and Problems of Acoustics. McGraw-Hill, New York (1971)

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. MOE Key Laboratory of Structure Mechanics and Control for Aircraft, Nanjing University of Aeronautics and Astronautics, 210016, Nanjing, China

    Masakazu Haraguchi & Hai Yan Hu

Authors
  1. Masakazu Haraguchi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Hai Yan Hu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Masakazu Haraguchi.

Additional information

The project supported by the National Natural Science Foundation of China (10532050).

Rights and permissions

Reprints and permissions

About this article

Cite this article

Haraguchi, M., Hu, H.Y. Stability analysis of a noise control system in a duct by using delay differential equation. Acta Mech Sin 25, 131–137 (2009). https://doi.org/10.1007/s10409-008-0196-4

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10409-008-0196-4

Keywords

Search

Navigation