Skip to main content
SpringerLink
Log in

Magnetohydrodynamics instability of interfacial waves between two immiscible incompressible cylindrical fluids

  • Research Paper
  • Published:
Acta Mechanica Sinica Aims and scope Submit manuscript

Abstract

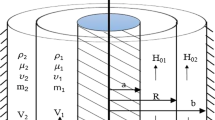
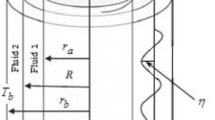
The problem of nonlinear instability of interfacial waves between two immiscible conducting cylindrical fluids of a weak Oldroyd 3-constant kind is studied. The system is assumed to be influenced by an axial magnetic field, where the effect of surface tension is taken into account. The analysis, based on the method of multiple scale in both space and time, includes the linear as well as the nonlinear effects. This scheme leads to imposing of two levels of the solvability conditions, which are used to construct like-nonlinear Schrödinger equations (l-NLS) with complex coefficients. These equations generally describe the competition between nonlinearity and dispersion. The stability criteria are theoretically discussed and thereby stability diagrams are obtained for different sets of physical parameters. Proceeding to the nonlinear step of the problem, the results show the appearance of dual role of some physical parameters. Moreover, these effects depend on the wave kind, short or long, except for the ordinary viscosity parameter. The effect of the field on the system stability depends on the existence of viscosity and differs in the linear case of the problem from the nonlinear one. There is an obvious difference between the effect of the three Oldroyd constants on the system stability. New instability regions in the parameter space, which appear due to nonlinear effects, are shown.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Pushkar E.A.: Gasdynamic analogies in problems of the oblique interaction of MHD shock waves. Fluid Dyn. Translated from Izvestiya Rossiiskoi Academii Nauk, Mekhanika Zhidkosti i Gaza 36(6), 989–1003 (2001)

    MATH  MathSciNet  Google Scholar 

  2. El-Sayed M.F.: Magnetohydrodynamic stability of two streaming superposed viscoelastic conducting fluids. Z. Naturforsch. 56a, 416–424 (2001)

    Google Scholar 

  3. Ilin K.I., Trakhinin Y.L., Vladimirov V.A.: The stability of steady MHD flows with current-vortex sheets. Phys. Plasmas 10, 2649–2658 (2003)

    Article  MathSciNet  Google Scholar 

  4. Blokhin A., Trakhinin Yu.: Stability of Strong Discontinuities in Magnetohydrodynamics and Electrohydrodynamics. Nova Science Publishers, New York (2003)

    Google Scholar 

  5. Shirota, T.: Regularity of solutions to mixed problems of linearized. [M.H.D. equations]. Nara Women’s University. Koukyuroku Math. 1, 1–42 (1994) (in Japanese)

  6. Malik S.K., Singh M.: Nonlinear focusing and the Kelvin–Helmholtz instability in ferrofluid/non-magnetic fluid systems. Phys. Fluids 31, 1069–1073 (1988)

    Article  Google Scholar 

  7. El-Dib Y.O.: Nonlinear stability of Kelvin–Helmholtz waves in magnetic fluids stressed by a time-dependent acceleration and a tangential magnetic field. J. Plasma Phys. 55, 219–234 (1996)

    Article  Google Scholar 

  8. Rajagopal K.R., Bhatnagar R.K.: Exact solutions for some simple flows of an Oldroyd-B fluid. Acta Mech. 113, 233–239 (1995)

    Article  MATH  MathSciNet  Google Scholar 

  9. Rajagopal K.R.: On an exact solution for the flow of an Oldroyd-B fluid. Bull. Tech. Univ. Istanbul 47, 617–623 (1996)

    Google Scholar 

  10. Pontrelli G., Bhatnagar R.K.: Flow of a viscoelastic fluid between two rotating circular cylinders subject to suction or injection. Int. J. Numer. Methods Fluids 24, 337–349 (1997)

    Article  MATH  MathSciNet  Google Scholar 

  11. Hayat T., Siddiqui A.M., Asghar S.: Some simple flows of an Oldroyd-B fluid. Int. J. Eng. Sci. 39, 135–147 (2001)

    Article  Google Scholar 

  12. Hayat T., Hutter K., Asghar S., Siddiqui A.M.: MHD flows of an Oldroyd-B fluid. Math. Comput. Modell. 36, 987–995 (2002)

    Article  MATH  MathSciNet  Google Scholar 

  13. Ray R.N., Samad A.: Chaudhury, T.K.: Hydromagnetic stability of plane Poiseuille flow of an Oldroyd fluid. Acta Mech. 143, 155–164 (2000)

    Article  MATH  Google Scholar 

  14. Baris S.: Flow of an Oldroyd 6-constant fluid between intersecting planes, one of which is moving. Acta Mech. 147, 125–135 (2001)

    Article  MATH  Google Scholar 

  15. Wang Y., Hayat T., Hutter K.: On non-linear magnetohydrodynamic problems of an Oldroyd 6-constant fluid. Int. J. Nonlin. Mech. 40, 49–58 (2005)

    Article  MATH  Google Scholar 

  16. Moatimid G.M., El-Dib Y.O.: Nonlinear Kelvin–Helmholtz instability of Oldroydian viscoelastic fluid in porous media. Physica A 333, 41–64 (2004)

    Article  Google Scholar 

  17. Hayat T., Khan M., Ayub M.: Exact solutions of flow problems of an Oldroyd-B fluid. Appl. Math. Comput. 151, 105–119 (2004)

    Article  MATH  MathSciNet  Google Scholar 

  18. Hayat T., Nadeem S., Asghar S.: Hydromagnetic couette flow of an Oldroyd-B fluid in a rotating system. Int. J. Eng. Sci. 42, 65–78 (2004)

    Article  MathSciNet  Google Scholar 

  19. Hayat T., Wang Y., Hutter K., Asghar S., Siddiqui A.M.: Peristaltic transport of an Oldroyd-B fluid in a planar channel. Math. Problems Eng. 4, 347–376 (2004)

    Article  MathSciNet  Google Scholar 

  20. Khan M., Hayat T., Asghar S.: Exact solution for MHD flow of a generalized Oldroyd-B fluid with modified Darcys law. Int. J. Eng. Sci. 44, 333–339 (2006)

    Article  MathSciNet  Google Scholar 

  21. Hayat T., Hussain M., Khan M.: Hall effect on flows of an Oldroyd-B fluid through porous medium for cylindrical geometries. Comput. Math. Appl. 52, 269–282 (2006)

    Article  MATH  MathSciNet  Google Scholar 

  22. Khan M., Maqbool K., Hayat T.: Influence of Hall current on the flows of a generalized Oldroyd-B fluid in a porous space. Acta Mech. 184, 1–13 (2006)

    Article  MATH  Google Scholar 

  23. Hayat T., Khan S.B., Khan M.: The influence of Hall current on the rotating oscillating flows of an Oldroyd-B fluid in a porous medium. Nonlin. Dyn. 47, 353–362 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  24. Hayat T., Khan M., Wang Y.: Non-Newtonian flow between concentric cylinders. Commun. Nonlin. Sci. Numer. Simul. 11, 297–305 (2006)

    Article  MATH  MathSciNet  Google Scholar 

  25. Hayat T., Khan M., Sajid M., Ayub M.: Steady flow of an Oldroyd 8-constant fluid between coaxial cylinders in a porous medium. J. Porous Media 9(8), 709–722 (2006)

    Article  Google Scholar 

  26. Hayat T., Khan M., Ayub M.: The effect of the slip condition on flows of an Oldroyd 6-constant fluid. J. Comput. Appl. Math. 202, 402–413 (2007)

    Article  MATH  MathSciNet  Google Scholar 

  27. Zakaria K.: Nonlinear instability of a liquid jet in the presence of a uniform electric field. Fluid Dyn. Res. 26, 405–420 (2000)

    Article  MATH  MathSciNet  Google Scholar 

  28. Gill G.K., Trehan S.K.: Nonlinear instabilities in superposed fluids in the presence of adsorption. Int. J. Eng. Sci. 34(2), 213–226 (1996)

    Article  MATH  MathSciNet  Google Scholar 

  29. Chandrasekhar S.: Hydrodynamic and Hydromagnetic Stability. Oxford University Press, Oxford (1961)

    MATH  Google Scholar 

  30. Lee D.S.: Nonlinear waves on the surface of a magnetohydrodynamic fluid column. Z. Naturforsch. 56a, 585–595 (2001)

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Faculty of Science, Tanta University, Tanta, Egypt

    Kadry Zakaria, Magdy A. Sirwah & Ahmed Assaf

Authors
  1. Kadry Zakaria
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Magdy A. Sirwah
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Ahmed Assaf
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ahmed Assaf.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Zakaria, K., Sirwah, M.A. & Assaf, A. Magnetohydrodynamics instability of interfacial waves between two immiscible incompressible cylindrical fluids. Acta Mech Sin 24, 497–514 (2008). https://doi.org/10.1007/s10409-008-0168-8

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10409-008-0168-8

Keywords

Search

Navigation