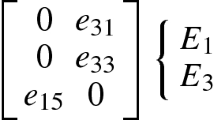Skip to main content
SpringerLink
Log in

A continuum damage model for piezoelectric materials

  • Research Paper
  • Published:
Acta Mechanica Sinica Aims and scope Submit manuscript

Abstract

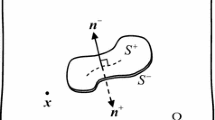
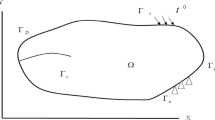
In this paper, a constitutive model is proposed for piezoelectric material solids containing distributed cracks. The model is formulated in a framework of continuum damage mechanics using second rank tensors as internal variables. The Helmhotlz free energy of piezoelectric materials with damage is then expressed as a polynomial including the transformed strains, the electric field vector and the tensorial damage variables by using the integrity bases restricted by the initial orthotropic symmetry of the material. By using the Talreja’s tensor valued internal state damage variables as well as the Helmhotlz free energy of the piezoelectric material, the constitutive relations of piezoelectric materials with damage are derived. The model is applied to a special case of piezoelectric plate with transverse matrix cracks. With the Kirchhoff hypothesis of plate, the free vibration equations of the piezoelectric rectangular plate considering damage is established. By using Galerkin method, the equations are solved. Numerical results show the effect of the damage on the free vibration of the piezoelectric plate under the close-circuit condition, and the present results are compared with those of the three-dimensional theory.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Moore, R.H., Dillard, D.A.: Time-dependent matrix cracking in cross-ply laminates. Composites Sci. Technol. 39, 1–12 (1990)

    Article  Google Scholar 

  2. Park, S.W., Schapery, R.A.: A viscoelastic constitutive model for particulate composites with growing damage. Int. J. Solids Struct. 34, 931–947 (1997)

    Article  MATH  Google Scholar 

  3. Luo, J.J., Daniel, I.M.: A cylinder model for characterization of deformation and damage development in a unidirectional composite. Composites Sci. Technol. 60, 2791–2802 (2000)

    Article  Google Scholar 

  4. Deng, H., Nemat-Nasser, S.: Microcrack arrays in isotropic solids. Mech. Mater. 13, 15–16 (1992)

    Article  Google Scholar 

  5. Zheng, Y.F., Fu, Y.M.: Analysis of the nonlinear vibration for symmetric angle-ply laminated viscoelastic plates with damage. Acta Mech. Sin. 21, 459–466 (2005)

    Article  Google Scholar 

  6. Mindlin, R.D.: Forced thickness-shear and flexural vibration of piezoelectric crystal plates. J. Appl. Phys. 23, 83–88 (1952)

    Article  MATH  MathSciNet  Google Scholar 

  7. Tiersten, H.F.: Linear Piezoelectric Plate Vibrations. Plenum Press, New York (1978)

    Google Scholar 

  8. Chandrashekhara, K., Thenneti, R.: Termally induced vibration suppression of laminated plates with piezoelectric sensors and actuators. Smart Mater. Struct. 4, 281–290 (1995)

    Article  Google Scholar 

  9. Zhou, X., Chattopadhyay, A., Gu, H.Z.: Dynamic response of smart composites using a coupled thermo-piezoelectric mechanical mode. AIAA J. 38, 1939–1948 (2000)

    Google Scholar 

  10. Wang, B., Rogers, A.: Laminate plate theory for spatially distributed induced strain actuators. J. Composite Mater. 25, 433–452 (1991)

    Google Scholar 

  11. Tzou, H.S., Gadre, M.: Theoretical analysis of a multi-layered thin shell coupled with piezoelectric shell actuators for distributed vibration controls. J. Sound Vib. 132, 433–450 (1989)

    Article  Google Scholar 

  12. Xu, K.M., Noor, A.K., Tang, Y.Y.: Three-dimensional solutions for free vibration of initially stressed thermoelectroelastic multilayered plates. Comput. Methods Appl. Mech. Eng. 141, 125–139 (1997)

    Article  MATH  Google Scholar 

  13. Mitchell, J.A., Reddy, J.N.: A refined hybrid plate theory for composite laminates with piezoelectric laminate. Int. J. Solid Struct. 32, 2345–2367 (1996)

    Article  Google Scholar 

  14. Rao, S.S., Sunar, M.: Piezoelectricity and its use in disturbance sensing and control of flexible structures: a survey. Appl. Mech. Rev 47, 113–123 (1994)

    Article  Google Scholar 

  15. Tauchert, T.R.: Piezothermoelastic behavior of a laminated plate. J. Thermal Stress 15, 25–37 (1992)

    Article  Google Scholar 

  16. Zheng, Y.F., Fu, Y.M.: Nonlinear dynamic stability for piezoelectric laminated plate with damage (in Chinese). Chin. J. Theor. Appl. Mech. 38, 570–576 (2006)

    Google Scholar 

  17. Yang, G.S.: Damage Mechanics and Composites Damage (in Chinese). National Defense Industry Press, Beijing (1994)

    Google Scholar 

  18. Spenser: Theory of Invariable (the third volume) (in Chinese). Phoenix Science Press, Nanjing, (1982)

  19. Duan, W.H., Quek, S.T., Wang, Q.: Free vibration analysis of piezoelectric coupled thin and thick annular plate. J. Sound Vib. 28, 119–139 (2005)

    Article  Google Scholar 

  20. Piotr, C.: Three-dimensional natural vibration analysis and energy considerations for a piezoelectric rectangular plate. J. Sound Vib. 283, 1093–1113 (2005)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. College of Mechanics and Aerospace, Hunan University, Changsha, 410082, China

    Yiming Fu & Xianqiao Wang

Authors
  1. Yiming Fu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xianqiao Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yiming Fu.

Additional information

The project supported by the National Natural Science Foundation of China (10572049).

The English text was polished by Keren Wang.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Fu, Y., Wang, X. A continuum damage model for piezoelectric materials. Acta Mech. Sin. 24, 171–179 (2008). https://doi.org/10.1007/s10409-007-0133-y

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10409-007-0133-y

Keywords

Search

Navigation