Skip to main content
SpringerLink
Log in

Fluid rheological effects on particle migration in a straight rectangular microchannel

  • Research Paper
  • Published:
Microfluidics and Nanofluidics Aims and scope Submit manuscript

Abstract

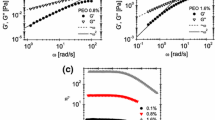
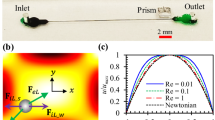
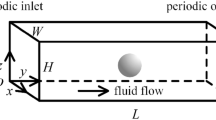
There has recently been a significantly increasing interest in the passive manipulation of particles in the flow of non-Newtonian fluids through microchannels. However, an accurate and comprehensive understanding of the various fluid rheological effects on particle migration is still largely missing. We present in this work a systematic experimental study of both the individual and the combined effects of fluid inertia, elasticity, and shear thinning on the motion of rigid spherical particles in a straight rectangular microchannel. We first study the sole effect of each of these rheological properties in a Newtonian fluid, purely elastic (i.e., Boger) fluid, and purely shear-thinning (i.e., pseudoplastic) fluid, respectively. We then study the combined effects of two or all of these rheological properties in a pseudoplastic fluid and two types of elastic shear-thinning fluids, respectively. We find that the fluid elasticity effect directs particles toward the centerline of the channel while the fluid shear-thinning effect causes particle migration toward both the centerline and corners. These two effects are combined with the fluid inertial effect to understand the particle migration in inertial pseudoplastic and viscoelastic fluid flows.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  • Amini H, Lee W, Di Carlo D (2014) Inertial microfluidic physics. Lab Chip 14:2739–2761

    Article  Google Scholar 

  • Asghari M, Serhatlioglu M, Ortaç B, Solmaz ME, Elbuken C (2017) Sheathless microflow cytometry using viscoelastic fluids. Sci Rep 7:12342. https://doi.org/10.1038/s41598-017-12558-2

    Article  Google Scholar 

  • Asmolov ES (1999) The inertial lift on a spherical particle in a plane Poiseuille flow at large channel Reynolds number. J Fluid Mech 381:63–87

    Article  MATH  Google Scholar 

  • Barnes HA, Hutton JF, Walters K (1989) An introduction to rheology. Elsevier, Amsterdam

    MATH  Google Scholar 

  • Bird RB, Armstrong RC, Hassager O (1977) Dynamics of polymeric liquids, vol 1. Wiley-Interscience, Hoboken

    Google Scholar 

  • Cheng NS (2008) Formula for the viscosity of a glycerol–water mixture. Ind Eng Chem Res 47:3285–3288

    Article  Google Scholar 

  • D’Avino G, Maffettone PL (2015) Particle dynamics in viscoelastic liquids. J Non-Newton Fluid Mech 215:80–104

    Article  MathSciNet  Google Scholar 

  • D’Avino G, Romeo G, Villone MM, Greco F, Netti PA, Maffettone PL (2012) Single line particle focusing induced by viscoelasticity of the suspending liquid: theory, experiments and simulations to design a micropipe flow-focuser. Lab Chip 12:1638–1645

    Article  Google Scholar 

  • D’Avino G, Greco F, Maffettone PL (2017) Particle migration due to viscoelasticity of the suspending liquid and its relevance in microfluidic devices. Annu Rev Fluid Mech 49:341–360

    Article  MathSciNet  MATH  Google Scholar 

  • Del Giudice F, Romeo G, D’Avino G, Greco F, Netti PA, Maffettone PL (2013) Particle alignment in a viscoelastic liquid flowing in a square-shaped microchannel. Lab Chip 13:4263–4271

    Article  Google Scholar 

  • Del Giudice F, D’Avino G, Greco F, Netti PA, Maffettone PL (2015) Effect of fluid rheology on particle migration in a square-shaped microchannel. Microfluid Nanofluid 19:95–104

    Article  Google Scholar 

  • Del Giudice F, Sathish S, D’Avino G, Shen AQ (2017) “From the edge to the center”: viscoelastic migration of particles and cells in a strongly shear-thinning liquid flowing in a microchannel. Anal Chem 89:13146–13159

    Article  Google Scholar 

  • Di Carlo D (2009) Inertial microfluidics. Lab Chip 9:3038–3046

    Article  Google Scholar 

  • Di Carlo D, Edd JF, Humphry KJ, Stone HA, Toner M (2009) Particle segregation and dynamics in confined flows. Phy Rev Lett 102:094503

    Article  Google Scholar 

  • Gauthier F, Goldsmith HL, Mason SG (1971a) Particle motions in non-Newtonian media. Rheol Acta 10:344–364

    Article  Google Scholar 

  • Gauthier F, Goldsmith HL, Mason SG (1971b) Particle motions in non-Newtonian media. II. Poiseuille flow. Trans Soc Rheol 15:297–330

    Article  Google Scholar 

  • Hejazian M, Li W, Nguyen NT (2015) Lab on a chip for continuous-flow magnetic cell separation. Lab Chip 15:959–970

    Article  Google Scholar 

  • Ho BP, Leal LG (1974) Inertial migration of rigid spheres in two-dimensional unidirectional flows. J Fluid Mech 65:365–400

    Article  MATH  Google Scholar 

  • Ho BP, Leal LG (1976) Migration of rigid spheres in a two-dimensional unidirectional shear flow of a second-order fluid. J Fluid Mech 76:783–799

    Article  MATH  Google Scholar 

  • Huang PY, Joseph DD (2000) Effects of shear thinning on migration of neutrally buoyant particles in pressure driven flow of Newtonian and viscoelastic fluids. J Non-Newton Fluid Mech 90:159–185

    Article  MATH  Google Scholar 

  • Huang L, Bian S, Cheng Y, Shi G, Liu P, Ye X, Wang W (2017) Microfluidics cell sample preparation for analysis: advances in efficient cell enrichment and precise single cell capture. Biomicrofluid 11:011501

    Article  Google Scholar 

  • James DF (2009) Boger fluids. Annu Rev Fluid Mech 41:129–142

    Article  MATH  Google Scholar 

  • Japper-Jaafar A, Escudier MP, Poole RJ (2010) Laminar, transitional and turbulent annular flow of drag-reducing polymer solutions. J Non-Newton Fluid Mech 165:1357–1372

    Article  MATH  Google Scholar 

  • Kang K, Lee SS, Hyun K, Lee SJ, Kim JM (2013) DNA-based highly tunable particle focuser. Nat Commun 4:2567

    Google Scholar 

  • Karimi A, Yazdi S, Ardekani AM (2013) Hydrodynamic mechanisms of cell and particle trapping in microfluidics. Biomicrofluid 7:021501

    Article  Google Scholar 

  • Karnis A, Mason SG (1966) Particle motions in sheared suspensions. XIX. Viscoelastic media. Trans Soc Rheol 10:571–592

    Article  Google Scholar 

  • Karnis A, Goldsmith HL, Mason SG (1963) Axial migration of particles in Poiseuille flow. Nature 200:159–160

    Article  Google Scholar 

  • Kayani AA, Khoshmanesh K, Ward SA, Mitchell A, Kalantar-Zadeh K (2012) Optofluidics incorporating actively controlled micro- and nano-particles. Biomicrofluid 6:031501

    Article  Google Scholar 

  • Kim B, Kim JM (2016) Elasto-inertial particle focusing under the viscoelastic flow of DNA solution in a square channel. Biomicrofluid 10:024111

    Article  Google Scholar 

  • Leal LG (1979) The motion of small particles in non-Newtonian fluids. J Non-Newton Fluid Mech 5:33–78

    Article  MATH  Google Scholar 

  • Leal LG (1980) Particle motions in a viscous fluid. Annu Rev Fluid Mech 12:435–476

    Article  MathSciNet  MATH  Google Scholar 

  • Lee DJ, Brenner H, Youn JR, Song YS (2013) Multiplex particle focusing via hydrodynamic force in viscoelastic fluids. Sci Rep 3:3258

    Article  Google Scholar 

  • Leshansky AM, Bransky A, Korin N, Dinnar U (2007) Tunable nonlinear viscoelastic “focusing” in a microfluidic device. Phys Rev Lett 98:234501

    Article  Google Scholar 

  • Li M, Li WH, Zhang J, Alici G, Wen W (2014) A review of microfabrication techniques and dielectrophoretic microdevices for particle manipulation and separation. J Phys D 47:063001

    Article  Google Scholar 

  • Li G, McKinley GH, Ardekani AM (2015) Dynamics of particle migration in channel flow of viscoelastic fluids. J Fluid Mech 785:486–505

    Article  MathSciNet  MATH  Google Scholar 

  • Li D, Lu X, Xuan X (2016) Viscoelastic separation of particles by size in straight rectangular microchannels: a parametric study for a refined understanding. Anal Chem 88:12303–12309

    Article  Google Scholar 

  • Liang L, Zhu J, Xuan X (2011) Three-dimensional diamagnetic particle deflection in ferrofluid microchannel flows. Biomicrofluid 5:034110

    Article  Google Scholar 

  • Lim EJ, Ober TJ, Edd JF, Desai SP, Neal D, Bong KW, Doyle PS, McKinley GH, Toner M (2014a) Inertio-elastic focusing of bioparticles in microchannels at high throughput. Nat Commun 5:4120

    Google Scholar 

  • Lim H, Nam J, Shin S (2014b) Lateral migration of particles suspended in viscoelastic fluids in a microchannel flow. Microfluid Nanofluid 17:683–692

    Article  Google Scholar 

  • Liu C, Hu G (2017) High-throughput particle manipulation based on hydrodynamic effects in microchannels. Micromachines 8:73

    Article  Google Scholar 

  • Liu C, Xue C, Chen X, Shan L, Tian Y, Hu G (2015a) Size-based separation of particles and cells utilizing viscoelastic effects in straight microchannels. Anal Chem 87:6041–6048

    Article  Google Scholar 

  • Liu C, Hu G, Jiang X, Sun J (2015b) Inertial focusing of spherical particles in rectangular microchannels over a wide range of Reynolds numbers. Lab Chip 15:1168–1177

    Article  Google Scholar 

  • Liu C, Ding B, Xue C, Tian Y, Hu G, Sun J (2016) Sheathless focusing and separation of diverse nanoparticles in viscoelastic solutions with minimized shear thinning. Anal Chem 88:12547–12553

    Article  Google Scholar 

  • Lu X, Xuan X (2015) Continuous microfluidic particle separation via elasto-inertial pinched flow fractionation. Anal Chem 87:6389–6396

    Article  Google Scholar 

  • Lu X, Zhu L, Hua RM, Xuan X (2015) Continuous sheath-free separation of particles by shape in viscoelastic fluids. Appl Phys Lett 107:264102

    Article  Google Scholar 

  • Lu X, Liu C, Hu G, Xuan X (2017) Particle manipulations in non-Newtonian microfluidics: a review. J Colloid Interface Sci 500:182–201

    Article  Google Scholar 

  • Martel JM, Toner M (2014) Inertial focusing in microfluidics. Annu Rev Biomed Eng 16:371–396

    Article  Google Scholar 

  • Nam J, Lee Y, Shin S (2011) Size-dependent microparticles separation through standing surface acoustic waves. Microfluid Nanofluid 11:317–326

    Article  Google Scholar 

  • Nam J, Tan JK, Khoo BL, Namgung B, Leo HL, Lim CT, Kim S (2015) Hybrid capillary-inserted microfluidic device for sheathless particle focusing and separation in viscoelastic flow. Biomicrofluid 9:064117

    Article  Google Scholar 

  • Nilsson J, Evander M, Hammarstrom B, Laurell T (2009) Review of cell and particle trapping in microfluidic systems. Anal Chim Acta 649:141–157

    Article  Google Scholar 

  • Poole RJ, Escudier MP (2004) Turbulent flow of viscoelastic liquids through an axisymmetric sudden expansion. J Non-Newton Fluid Mech 117:25–46

    Article  Google Scholar 

  • Rodd LE, Scott TP, Boger DV, Cooper-White JJ, McKinley GH (2005) The inertio-elastic planar entry flow of low-viscosity elastic fluids in micro-fabricated geometries. J Non-Newton Fluid Mech 129:1–22

    Article  Google Scholar 

  • Romeo G, D’Avino G, Greco F, Netti PA, Maffettone PL (2013) Viscoelastic flow-focusing in microchannels: scaling properties of the particle radial distributions. Lab Chip 13:2802–2807

    Article  Google Scholar 

  • Sajeesh P, Sen AK (2014) Particle separation and sorting in microfluidic devices: a review. Microfluid Nanofluid 17:1–52

    Article  Google Scholar 

  • Segre G, Silberberg A (1961) Radial particle displacements in Poiseuille flow of suspensions. Nature 189:209–210

    Article  Google Scholar 

  • Seo KW, Byeon HJ, Huh HK, Lee SJ (2014a) Particle migration and single-line particle focusing in microscale pipe flow of viscoelastic fluids. RSC Adv 4:3512–3520

    Article  Google Scholar 

  • Seo KW, Kang YJ, Lee SJ (2014b) Lateral migration and focusing of microspheres in a microchannel flow of viscoelastic fluids. Phys Fluids 26:063301

    Article  Google Scholar 

  • Seo KW, Ha YR, Lee SJ (2014c) Vertical focusing and cell ordering in a microchannel via viscoelasticity: applications for cell monitoring using a digital holographic microscopy. Appl Phys Lett 104:213702

    Article  Google Scholar 

  • Song HY, Lee SH, Salehiyan R, Hyun K (2016) Relationship between particle focusing and dimensionless numbers in elasto-inertial focusing. Rheol Acta 55:889–900

    Article  Google Scholar 

  • Tarn MD, Lopez-Martinez MJ, Pamme N (2014) On-chip processing of particles and cells via multilaminar flow streams. Anal Bioanal Chem 406:139–161

    Article  Google Scholar 

  • Villone MM, D’Avino G, Hulsen MA, Greco F, Maffettone PL (2013) Particle motion in square channel flow of a viscoelastic liquid: migration vs. secondary flows. J Non-Newton Fluid Mech 195:1–8

    Article  MATH  Google Scholar 

  • Xiang N, Dai Q, Ni Z (2016a) Multi-train elasto-inertial particle focusing in straight microfluidic channels. Appl Phys Lett 109:134101

    Article  Google Scholar 

  • Xiang N, Zhang X, Dai Q, Cheng J, Chen K, Ni Z (2016b) Fundamentals of elasto-inertial particle focusing in curved microfluidic channels. Lab Chip 16:2626–2635

    Article  Google Scholar 

  • Xuan X, Zhu J, Church C (2010) Particle focusing in microfluidic devices. Microfluid Nanofluid 9:1–16

    Article  Google Scholar 

  • Yan S, Zhang J, Yuan D, Li W (2017) Hybrid microfluidics combined with active and passive approaches for continuous cell separation. Electrophoresis 38:238–249

    Article  Google Scholar 

  • Yang S, Kim JY, Lee SJ, Lee SS, Kim JM (2011) Sheathless elasto-inertial particle focusing and continuous separation in a straight rectangular microchannel. Lab Chip 11:266–273

    Article  Google Scholar 

  • Yang S, Lee SS, Ahn SW, Kang K, Shim W, Lee G, Hyun K, Kim JM (2012) Deformability-selective particle entrainment and separation in a rectangular microchannel using medium viscoelasticity. Soft Matter 8:5011–5019

    Article  Google Scholar 

  • Yasuda K, Armstrong RC, Cohen RE (1981) Shear flow properties of concentrated solutions of linear and star branched polystyrenes. Rheol Acta 20:163–178

    Article  Google Scholar 

  • Yuan D, Zhang J, Yan S, Pan C, Alici G, Nguyen NT, Li W (2015) Dean-flow-coupled elasto-inertial three-dimensional particle focusing under viscoelastic flow in a straight channel with asymmetrical expansion–contraction cavity arrays. Biomicrofluid 9:044108

    Article  Google Scholar 

  • Yuan D, Zhao Q, Yan S, Tang SY, Alici G, Zhang J, Li W (2018) Recent progress of particle migration in viscoelastic fluids. Lab Chip. https://doi.org/10.1039/C7LC01076A

    Google Scholar 

  • Zhang J, Yan S, Yuan D, Alici G, Nguyen NT, Warkiani ME, Li W (2016) Fundamentals and applications of inertial microfluidics: a review. Lab Chip 16:10–34

    Article  Google Scholar 

Download references

Acknowledgments

This work was supported in part by NSF under Grant CBET-1150670 and by Clemson University through a SEED Grant.

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Clemson University, Clemson, SC, 29634-0921, USA

    Di Li & Xiangchun Xuan

Authors
  1. Di Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xiangchun Xuan
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Di Li.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Li, D., Xuan, X. Fluid rheological effects on particle migration in a straight rectangular microchannel. Microfluid Nanofluid 22, 49 (2018). https://doi.org/10.1007/s10404-018-2070-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10404-018-2070-4

Keywords

Search

Navigation