Effectiveness of flow obstructions in enhancing electro-osmotic flow

Abstract

In this paper the influence of obstructions on microchannel electro-osmotic flow is investigated for the first time. To carry out such a study, regular obstructions are introduced into microchannels and flow rates are numerically calculated. The effect of channel width on flow rates is analysed on both free and obstructed channels. The solid material considered for channel walls and obstructions is silicon, and the electrolyte is deionised water. The parameters studied include channel width, obstruction size and effective porosity of the channel. The effective porosity is varied between 0.4 and 0.8 depending on other chosen parameters. The results clearly demonstrate that, under the analysed conditions, introduction of obstructions into channels wider than $100\,\upmu \hbox {m}$ enhances the flow rate induced by electro-osmosis.

1 Introduction

Electro-osmotic flow (EOF)-driven systems have been employed in various branches of engineering and technology, such as biomedical, geophysical, energy and chemical. Over the last century, electro-kinetic effects have been widely exploited in micro- and nanofluidic devices. The most common applications include pumping (Berrouche et al. 2009; Chen et al. 2008; Kang et al. 2007; Li et al. 2013b; Wang et al. 2006, 2009; Yao and Santiago 2003; Yao et al. 2006), capillary electrochromatography (Liapis and Grimes 2000; Rathore and Horváth 1997) and recently dehumidification and regeneration of desiccant structures (Li et al. 2013a, b). EOF in micro- and nanosystems with and without porous media has been investigated both experimentally and numerically by many, and recently, the behaviour of non-Newtonian fluids under EOF has also been examined (Chen et al. 2014). Due to the dimensions involved in microchannels, producing experimental data is difficult and therefore numerical modelling is very useful in predicting EOF (Li et al. 2013a, b; Wang et al. 2006).

As introduced by Gouy (1910) and Chapman (1913), the internal potential for a planar surface can be described by the Poisson equation (see Sect. 2.1) that can be linearised for small values of electric potential by using the Debye–Hückel approximation (Patankar and Hu 1998). In numerical modelling of EOF in porous media, other simplifying hypotheses have been commonly assumed. Most authors have considered only the charge of channel walls neglecting that of solid particles (Scales 2004), both in the equation governing the internal potential and in that describing fluid flow. Recently, some researchers have attempted to estimate the contribution of solid particles to EOF. Several authors have analysed EOF at the pore level (Chen et al. 2014; Li et al. 2013a, b; Wang and Chen 2007; Wang et al. 2006), while others have used a generalised model for porous media flow and added a source term in the momentum equation, depending on the charge density of porous medium and the applied electrical field (Scales 2004; Tang et al. 2010). Although it has been found that the main driving force is due to the charged particles rather than the channel walls (Wang et al. 2006), it appears that the internal potential equation has not been appropriately modified to take into account the charge of solid particles, except for boundary conditions (Tang et al. 2010). To consider the charge of both solid particles and channel walls, Kang et al. (2005) split the velocity into two components and then coupled them to obtain the overall macroscopic EOF velocity. The first component was derived as per the fluid flow in standard channels, by assimilating the porous medium to an assembly of parallel tortuous cylinders. The second component was obtained by applying the Brinkman extension of the Darcy equation, in which the inertia terms were neglected because of the low Reynolds number. The dimensionless Darcy velocity was found to increase with the particles size, the applied electric field and the difference between zeta potential of particles and channel walls, and it was also found to decrease with increase in channel width.

Many authors have focused on EO porous pumps and found that the thermodynamic efficiency significantly increases with the addition of a porous medium in a channel, as much higher pumping pressures can be generated (Wang et al. 2006).

In general, the velocity has been found to increase with the increase in diameter of solid particles or pores (Berrouche et al. 2009; Chai et al. 2007; Chen et al. 2008; Kang et al. 2005; Tang et al. 2010; Wang and Chen 2007; Yao et al. 2006) and porosity (Chai et al. 2007; Tang et al. 2010; Wang and Chen 2007). Although EOF can be enhanced by increasing the contact surface between the electrolyte and the boundaries of charged particles, excessive reduction in void space between the particles (Kang et al. 2005) can substantially increase the viscous losses (Berrouche et al. 2009). Such losses can easily compromise the pressure generated by surface charge (Chai et al. 2007). The effect of the distance between solid particles on EOF has also been analysed in the past. By considering only the charge of solid particles, the maximum velocity was achieved for a distance between particles equal to five times that of the Debye length (see Sect. 2.2) (Li et al. 2013a). It appears that the EO driving force decreases when the distance between the particles is different from this value (Li et al. 2013a). When the gap between the particles is too small, the electric double layer of the particles overlaps and as a consequence the velocity decreases several orders of magnitude. An attempt to optimise the porosity has found that as the pore number density increases and the pore diameter decreases, both flow rate and pressure performance of porous membrane pumps increase (Yao et al. 2006). Cheema et al. (2013) found that EO pumping can be improved when the layers adjacent to the solid wall of the pump present higher porosity with respect to the central region. In this case, the velocity near the walls is larger and therefore variation in porosity near the wall cannot be neglected (Chai et al. 2007).

Chen et al. (2014) investigated the influence of the structure of porous media on EO permeability, that relates the average fluid velocity to the external electric field, and found that EO permeability grows monotonically with increasing porosity.

As mentioned before, EOF in porous media has been modelled by using a microscopic approach in many studies. It was found that the geometry used to approximate the morphology of porous media significantly affects the prediction of the volumetric flow rate that was observed to be greater in cylindrical and annular capillaries than in rectangular channels (Pascal et al. 2012). Morphology of porous media was also investigated by Wang (2012), who analysed the difference in terms of EOF permeability obtained by using granular, fibrous or network structures. He showed that at low porosity the network configuration enhanced EOF permeability, due to its highest surface/volume ratio, whereas at higher values of porosity the granular structure performed better, for its lower resistance to flow.

From the analysis of the available scientific literature on the subject of EOF in porous media, it appears that the work on that subject is quite heterogeneous in nature (Di Fraia et al. 2017). Although some important attempts have been made in the recent past, many of the fundamental aspects are still unclear. The two important issues that need a better understanding are: method of modelling EOF past obstructions and flow enhancement as a result of introducing obstructions confined in a microchannel. By focusing on these aspects the effectiveness of using flow obstructions in microchannels to enhance EOF should be determined with certainty.

The aim of this paper is to understand under which conditions the use of obstructions in microchannels can be useful to increase EO flow rate. For this reason, in the present work a well-defined porous medium represented by regular flow obstructions is studied by using a microscopic approach that provides details of flow structure at particle level (Massarotti et al. 2003). The interaction between obstruction boundaries and side walls, which affects the internal potential distribution, and consequently EOF, has been analysed. Fluid flow is modelled by using Navier–Stokes equations for incompressible flow that are solved by using a fully explicit artificial compressibility-based CBS (characteristic-based split) scheme (Nithiarasu 2003; Nithiarasu et al. 2016) through the channel. The momentum equation has been modified to include the electro-kinetic effects responsible for EOF into a source term. The effect of obstructions on the internal potential distribution is taken into account by introducing a novel reference length. To analyse the effectiveness of introducing porous media to enhance EOF, simulations have been carried out on microchannels with and without obstructions and the results are compared in terms of internal potential distribution, fluid velocity and flow rate. Furthermore, the model has been used to carry out a sensitivity analysis of these quantities on the channel width and on the topology of the obstructions.

The paper is organised into the following sections. In Sect. 2 the governing equations are briefly presented (for the sake of completeness the solution algorithm is described in “Appendix”). In Sect. 3 the numerical results are reported: firstly the results for fluid flow without obstructions are compared to their available analytical solutions; then, the model is used to assess the effect of channel width, particle size and porosity of the channel with obstructions on EOF. Finally, in Sect. 4, some conclusions are drawn.

2 Mathematical model and solution procedure

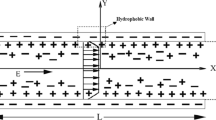
The electric field that generates electro-osmotic flow (EOF) is induced by the interaction between an external applied potential and the electric double layer (EDL), as shown in Fig. 1.

Fig. 1

Electro-kinetic effects in the electrical double layer induce the fluid flow that is approximately uniform outside the electrical double layer (the thickness of the electrical double layer is enlarged for the sake of clarity)

The electro-kinetic forces responsible for EOF are modelled through Laplace equation governing the external applied potential and Poisson–Boltzmann equation governing the EDL potential. These equations defining the electrical field are decoupled and solved separately from the Navier–Stokes equations, and their effect on the flow is taken into account through a source term of the momentum equation (Patankar and Hu 1998; Yang and Li 1998). Fluid flow is analysed through the Navier–Stokes equations that are temporally discretised by using the characteristic-based split (CBS) algorithm (Nithiarasu 2003; Nithiarasu et al. 2016), while the Galerkin approximation is used for spatial discretisation.

2.1 Governing equations

The external potential $\phi$ is governed by the Laplace equation of the type:

$$\sigma \frac{\partial ^2\phi }{\partial x_i^2} = 0$$

(1)

where $\sigma$ is the fluid electrical conductivity. The external electric field, $E_x$, and the external electric potential, $\phi$, are related via

$$E_x = -\frac{\partial \phi }{\partial x_i}$$

(2)

The electric double layer (EDL) potential, $\psi$, is described by the Poisson–Boltzmann equation, as follows:

$$\frac{\partial ^2\psi }{\partial x_i^2} = -\frac{\rho _E}{\varepsilon \varepsilon _0}$$

(3)

where $\varepsilon$ is the dielectric constant of the electrolyte, $\varepsilon _0$ is the permittivity of vacuum, and $\rho _E$ is the net charge density.

The equilibrium Boltzmann distribution equation can be used to predict the ionic number concentration in the case of fully developed flow with small Peclet numbers (Yang et al. 2001) and in the absence of overlapping of EDLs (Qu and Li 2000). The ions in the solution are assumed to be equal but opposite in charge, and they are related to their energy $\left( \textit{ze}\psi \right)$ as

$$n^+ = n_0 \exp {\left( -\frac{ze\psi }{k_\text{B} T}\right) }; \quad n^- = n_0 \exp {\left( \frac{ze\psi }{k_\text{B} T}\right) };$$

(4)

where $n^+$ and $n^-$ represent the number of positive and negative ions, respectively, $n_0$ is the ionic number concentration in the bulk solution, z is the valance of the ions, e is the elementary charge, $k_\text{B}$ is the Boltzmann’s constant, and T is the temperature in kelvin. The bulk ionic concentration $n_0$ can be obtained as

$$n_0 = cN_\text{A}$$

(5)

where c is the concentration of the electrolyte in moles and $N_\text{A}$ is Avogadro constant. Therefore, the net charge density can be defined as

$$\rho _E = ze\left( n^+-n^-\right)$$

(6)

Using hyperbolic functions, the net charge density can be expressed as

$$\rho _E = -2n_0 z e \sinh \left( \frac{ze\psi }{k_\text{B} T}\right)$$

(7)

The nonlinear Poisson–Boltzmann equation, obtained by substituting Eqs. (7) into (3), allows us to determine the internal potential distribution of the ions inside the fluid as

$$\frac{\partial ^2\psi }{\partial x_i^2} = \frac{2n_0 z e}{\varepsilon \varepsilon _0} \sinh \left( \frac{ze\psi }{k_\text{B} T}\right)$$

(8)

Fluid flow phenomena due to EO in microchannels can be modelled by using the modified incompressible Navier–Stokes equations that can be written as follows.

• Continuity equation

  $$\frac{\partial \rho }{\partial t} + \rho \frac{\partial u_i}{\partial x_i} = 0$$

  (9)

  where $\rho$ the fluid density and $u_i$ the fluid velocity components. By using the ideal gas law, the speed of sound c can be expressed as

  $$c^2 = \frac{\partial p}{\partial \rho }$$

  (10)

  where p is the pressure. The continuity equation can now be rewritten as follows

  $$\frac{1}{c^2} \frac{\partial p}{\partial t} = - \rho \frac{\partial u_i}{\partial x_i}$$

  (11)

  For incompressible flows, the speed of sound may be replaced with an artificial compressibility parameter, $\beta$, (Nithiarasu 2003).

• Momentum equation

  $$\rho \left( \frac{\partial u_i}{\partial t} + \frac{\partial \left( u_i u_j\right) }{\partial x_j}\right) = -\frac{\partial p}{\partial x_i} + \frac{\partial \tau _{ij}}{\partial x_i} + \rho _E E_x$$

  (12)

  where $\tau _{ij}$ are the deviatoric stress components, related to velocity as

  $$\tau _{ij} = \mu \left( \frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}\right)$$

  (13)

  in which $\mu$ is the dynamic viscosity. The last term of Eq. (12) takes into account the driving force of EOF due to the interaction between the EDL potential and the external electric field.

2.2 Dimensionless form of the governing equations

The dimensionless form of the governing equations for forced flow can be obtained through the following non-dimensional scales.

$$\begin{aligned} x^*_i= &\, {} \frac{x_i}{L_{\text{ref}}}; \quad \phi ^*= \frac{ze\phi }{k_\text{B} T}; \qquad \psi ^*= \frac{ze\psi }{k_\text{B} T}; \qquad \rho ^*= \frac{\rho }{\rho _{\text{ref}}};\\ u^*_i= &\, {} \frac{u_i}{u_{\text{ref}}}; \qquad u_{\text{ref}}= \frac{E_x \varepsilon \varepsilon _0 \zeta }{\mu }; \qquad t^*= \frac{t u_{\text{ref}}}{L_{\text{ref}}};\\ p^*= &\, {} \frac{p-p_{\text{ref}}}{\rho _{\text{ref}} u^2_{\text{ref}}}; \qquad \sigma ^*=\frac{\sigma }{\sigma _{\text{ref}}} \end{aligned}$$

• Laplace equation

  $$\sigma ^* \frac{\partial ^2\phi ^*}{\partial {x^*_i}^2} = 0$$

  (14)

• Poisson–Boltzmann equation

  $$\frac{\partial ^2\psi ^*}{\partial {x^*_i}^2} = -\left( \kappa L_{\text{ref}}\right) ^2 \sinh \left( \psi ^*\right)$$

  (15)

  where $\kappa$ is known as Debye length and corresponds to the EDL characteristic thickness (Patankar and Hu 1998)

  $$\kappa = \left( \frac{2n_0 z^2 e^2}{k_\text{B} T \varepsilon \varepsilon _0}\right) ^{1/2}$$

  and $L_{\text{ref}}$ is a reference length that can be derived as follows:

  $$L_{\text{ref}} = \frac{A_{\text{fluid}}}{L_{\text{chan}}} = \frac{A_{\text{chan}}-A_{\text{obstr}}}{L_{\text{chan}}}$$

  (16)

  where $A_{\text{fluid}}$ is the area of the channel occupied by the fluid, $L_{\text{chan}}$ is the length of the channel, $A_{\text{chan}}$ is the area of the channel, $A_{\text{obstr}}$ is the area of the channel occupied by the obstructions. For the sake of clarity these areas are shown in Fig. 2. Depending on $A_{\text{fluid}}$ an effective porosity $\Phi$ can be defined, as follows:

  $$\Phi = \frac{A_{\text{fluid}}}{A_{\text{chan}}}$$

  (17)

By using the effective porosity the reference length can be rewritten as

$$L_{\text{ref}} = \Phi W_{\text{chan}}$$

(18)

where $W_{\text{chan}}$ is the width of the channel. In plain channels $L_{\text{ref}}$ corresponds to the channel width (i.e. the distance between the two walls), consistent with the quantity commonly used in previous works concerning EOF. However in channels with obstructions, these reduce the area of the channel occupied by the fluid taking into account the variation of internal potential distribution due to the static charge of solid particles in addition to that of channel walls.

Fig. 2

Schematic of microchannel with obstructions

In unobstructed flow, flow rate has been found to increase as the ratio between channel width and the Debye length, $\kappa \cdot W$, is in the range of 1–100 and to be constant beyond this value (Rice and Whitehead 1965; Yao and Santiago 2003). When the channel width is much larger than the Debye length, the drag effect due to electro-kinetic forces of EDL decreases, and as a consequence EOF is reduced. Thus the use of charged flow obstructions to enhance EDL potential distribution can increase the range of effectiveness of EOF-driven systems.

Based on the above-defined quantities and scales, the non-dimensional form of the Navier–Stokes equations for these problems can be written as:

• Continuity equation

  $$\frac{1}{{\beta ^*}^2} \frac{\partial p^*}{\partial t^*} = - \rho ^* \frac{\partial u^*_i}{\partial x^*_i}$$

  (19)

  where the artificial compressibility parameter, $\beta$, Nithiarasu (2003) is locally calculated at each node as (Massarotti et al. 2006):

  $$\beta = \max \left( \eta , u_{\text{conv}}, u_{\text{diff}} \right)$$

  (20)

  The constant $\eta$ is assumed to be 0.5, $u_{\text{conv}}$ and $u_{\text{diff}}$ are the convective and diffusive velocities, respectively.

• Momentum equation

  $$\begin{aligned} \rho ^* \left( \frac{\partial u^*_i}{\partial t^*} + \frac{\partial \left( u^*_i u^*_j\right) }{\partial x^*_j}\right) =&-\frac{\partial p^*}{\partial x^*_i} + \frac{1}{Re} \frac{\partial ^2 u^*_i}{\partial {x^*_i}^2} \\&+\, J \sinh \left( \psi ^*\right) \left( \frac{\partial \phi ^*}{\partial {x^*_i}}\right) \end{aligned}$$

  (21)

  where

  $$\begin{aligned} Re=&\, {} \frac{\rho _{\text{ref}} u_{\text{ref}} L_{\text{ref}}}{\mu } = \rho _{\text{ref}} \left( \frac{E_x \varepsilon \varepsilon _0 \zeta }{\mu }\right) \left( \frac{L_{\text{ref}}}{\mu }\right) ;\\ J=&\, {} \frac{2n_0 k_\text{B} T}{u^2_{\text{ref}}\rho _{\text{ref}}}. \end{aligned}$$

  The above set of non-dimensional equations has been solved by using fully explicit artificial compressibility-based CBS scheme (Nithiarasu 2003; Nithiarasu et al. 2016), described in “Appendix” for the sake of completeness.

3 Results and discussion

A silicon microchannel of 30 $\mu \text{m}$ in width, characterised by an aspect ratio of 10, with deionised water as working fluid is considered as a reference case. The electrical conductivity, $\sigma$, and dynamic viscosity, $\mu$, are assumed to be constant. The parameters used in the present study are reported in Table 1.

Table 1 Parameters used in the numerical simulations

The flow past obstructions are investigated at the pore level, and the solid particles are assumed to be circular in shape. By fixing the effective porosity $\Phi$ equal to 0.8, three different particle sizes are considered, i.e. particles with diameter equal to 29, 16 and 12% of the channel width, hereafter, referred to as P29%, P16% and P12%, respectively. The layouts of these configurations of microchannel are shown in Fig. 3.

Fig. 3

Configurations of flow obstructions used in the simulations: P29% (a), P16% (b) and P12% (c)

The boundary conditions applied in this work are shown in Fig. 4.

Fig. 4

Schematic diagram of the rectangular 2D microchannel used in the simulations: plain channel on the left, channel with obstructions on the right

The channel walls and the boundaries of solid obstructions are assumed to be active with a prescribed non-dimensional zeta potential and to obey no-slip velocity boundary conditions. An applied external potential difference between the inlet and outlet is considered, and the normal components of velocity gradients are assumed to be zero at both inlet and outlet. The computation is started with prescribed zero velocity components as initial condition. The dimensional external potential difference between the inlet and outlet sections of the channel is fixed equal to 1 kV/m. The non-dimensional zeta potential value of −0.75, corresponding to −19 mV, is considered for both the channel walls and the solid particles. The value considered for the zeta potential imposed on the charged surfaces is derived from some experimental investigations carried out on electro-osmotic flow in silicon microchannels (Eng 2009; Eng and Nithiarasu 2009).

A set of 2D unstructured meshes, refined near all solid boundaries to capture the rapid change in both internal potential and velocity, is used. The details of the meshes used for plain channels and channels with obstructions are shown in Fig. 5. A mesh sensitivity study has been carried out to finalise the meshes used in the calculations.

Fig. 5

Details of the meshes used for fluid (a) and channels with obstructions, P29% (b), P16% (c) and P12% (d)

3.1 Comparison of results against analytical solutions

The numerical model described in “Appendix” is used to determine EOF in microchannels with and without solid obstructions. For a plain channel without obstructions, the flow results are compared against the available analytical solutions (Patankar and Hu 1998). For a two-dimensional rectangular channel, the analytical solution for the internal potential may be written as

$$\psi = \frac{\cosh \left[ \kappa a \left( y-1/2\right) \right] }{\cosh \left[ \kappa a /2 \right] }$$

(22)

where y is the distance from the wall. The analytical solution for the horizontal velocity component (Arnold 2007) may be written as

$$u = 1- \zeta \left( 2ln \frac{1 + \exp \left( -\kappa a y\right) \tanh \left( \frac{1}{4} \zeta \right) }{1 - \exp \left( -\kappa a y\right) \tanh \left( \frac{1}{4} \zeta \right) } \right)$$

(23)

In Fig. 6 the internal potential distribution and velocity profiles over half of the channel width are plotted and compared against the analytical solution. Since the analytical solution is derived for the linearised Poisson–Boltzmann equation, there is a slight discrepancy with the numerical results. The data of the simulations for velocity have been normalised in order to have a clear comparison with the analytical solution.

Fig. 6

Comparison of internal potential (a) and horizontal velocity (b), profiles against analytical solutions

3.2 Effect of obstructions on EOF

The internal potential distribution plays a fundamental role on EOF. The influence is highlighted in Fig. 7, where the profiles of internal potential and velocity are plotted, over half of the channel width, for the configuration P16% of the channel with obstructions and for the channel without obstructions.

Fig. 7

Non-dimensional internal potential (a) and velocity (b) profiles: results for the plain channel without obstructions and the microchannel filled with obstructions P16% at x/L = 5 and x/L = 10

The internal potential and horizontal velocity profiles are constant along the channel length for plain channel, while they change when obstructions are introduced. This is shown by plotting the quantities of interest at different sections of the channel: in the central section (i.e. x/L = 5), where the profile presents a discontinuity due to the obstruction of a particle, and at the outlet section (i.e. x/L = 10) with no obstructing particle. Although the internal potential is equal to zero in a larger section for the plain channel, a larger internal potential gradient near the wall produces a higher horizontal velocity than that of the channel with obstructions. The solid obstructions enhance the internal potential distribution thanks to their charged boundaries, but at the same time they increase the resistance to fluid flow.

3.3 Effect of microchannel width on EOF

In order to assess the conditions under which the use of flow obstructions positively affects EOF, the geometry has been investigated. A range of different channel widths, W, between 5 and 150 $\mu \text{m}$, has been investigated for microchannels with and without obstructions. As the channel width increases, the internal potential approaches zero in the central region of the channel, and the profile becomes steeper close to the walls. This behaviour is weaker in channels filled with obstructions in which the presence of charged particles balances the width effect, as shown in Fig. 8. In this figure, the internal potential profiles at the outlet of the channel for a channel without and with obstructions are shown at different channel widths. Both internal potential and width are non-dimensional, and only half width of the channel is presented. The effects of obstructions on EOF can be appreciated in Fig. 9, where the non-dimensional horizontal velocity profile at the outlet section of the channel is reported for plain microchannel and microchannel with obstructions.

Fig. 8

Non-dimensional internal potential distribution at different widths for plain microchannel (a) and microchannels with obstructions of diameter equal to 16% of the channel width (b)

Fig. 9

Non-dimensional outlet velocity profile at different widths for plain microchannel (a) and microchannels filled with obstructions of diameter equal to 16% of the channel width (b)

Since internal potential effect on EOF is introduced through a source term in momentum equation, confinement of internal potential variation close to walls produces little flow. For a plain fluid channel with no obstructions, the average velocity increases as the channel width is increased from 5 to 15$\mu m$, while beyond this value it rapidly decreases, as shown in Fig. 9b. This increase in velocity, initially, is a result of decrease in ratio of surface to cross-sectional areas, while EDL thickness remains constant. When flow obstructions are introduced in the microchannels, the average velocity increases beyond a channel width of 15 $\mu \text{m}$, indicating that the introduction of obstructions is effective beyond this channel width. However, the average velocity starts to decrease beyond a width of $60\,\mu \text{m}$, indicating that the interaction between the EDL of channel walls and obstruction boundaries becomes weaker in producing higher EO velocities. In addition, by comparing EOF in microchannels with and without obstructions, it is worth noticing that in plain channels the average velocity is higher than that of channels with obstructions for smaller microchannels, but it becomes significantly lower when the channel width is larger than $100\,\mu \text{m}$. Moreover, the rate of decrease in velocity in channels with obstructions is lower than that observed in plain channels.

As expected, in narrow channels, introducing obstructions produces higher drag resistance that undermines pressure generated by EO force. In addition EDLs overlap due to the short distance between adjacent particles. However, as the channel width is increased this trend is reversed and introduction of obstructions becomes more and more effective. On the other hand, when the width is too large, and the distance between the charged surfaces increases, the internal potential approaches zero in between obstructions, causing the average velocity to decrease. This effect is clearly noticed in Fig. 10, where the distribution of internal potential and horizontal velocity is reported for two different channel widths. Only part of the whole domain is plotted here to clearly view these details.

Fig. 10

Contours of internal potential (a) and (b) and horizontal velocity (c) and (d), for microchannel with obstructions at different widths: 60 $\mu \text{m}$ (on the left) and $150\,\mu \text{m}$ (on the right)

3.3.1 Width beyond which the solid obstruction is useful

In order to assess the effectiveness of using obstructions to enhance EOF, the flow rate has been determined for different channel widths and it is plotted in Fig. 11. From this figure it can be seen that for smaller plain channels the flow rate significantly grows as the width is increased. In all cases a rapid increase is observed at lower channel widths and the rate of increase is reduced beyond a channel width of $50\,\upmu \text{m}$. The plain microchannel without obstructions appears to be effective up to a channel width of $80\,\upmu \text{m}$, while beyond a width of $100\,\upmu \text{m}$, introducing flow obstructions enhances the flow rate further. As shown in Fig. 11 three geometric configurations have been studied. By keeping the effective porosity constant, the ratio between the channel width and the particle diameter is varied and assumed equal to 29, 16 and 12%. Thus three different particle distributions within the category of channel with obstructions are analysed. They are identified, respectively, as P29%, P16% and P12%. All the configurations enhance EOF as the channel width is increased, but P16% appears to be more effective. The flow rate increases up to a channel width of $120\,\upmu \text{m}$ when this distribution is used, while smaller and larger particles enhance flow only up to around 90 and 100$\,\upmu \text{m}$, respectively. The plain microchannels with no obstructions may be effective in pumping fluids up to a channel width of $100\,\upmu \text{m}$. Beyond this channel width however, introduction of obstructions can increase fluid flow.

Fig. 11

Flow rate at different widths of microchannels with and without obstructions

In the previous works concerning EOF, the velocity is often related to the EDL characteristic thickness, $\kappa ^{-1}$. Under the analysed conditions this thickness is around 1$\,\mu \text{m}$. When the quantity $W \cdot \kappa$ approaches 100, the velocity is expected to rapidly decrease, as observed by several authors (Rice and Whitehead 1965; Yao and Santiago 2003). This is however not the case for channels with obstructions. The value of $W \cdot \kappa$ is much larger than 100 before a decrease in velocity is observed. If however $L_{\text{ref}}$ from Eq. 16 is used to define the width, W, for channels with obstructions, the flow rate decreases as $W \cdot \kappa$ approaches 100.

3.4 Effect of particle sizes on EOF

The effect of particle size on EOF appears to be significant. Configurations P29% and P16% present a similar trend in terms of flow rate for channel widths of up to 80 $\mu \text{m}$: beyond this value it appears that for P29% EDL effect on flow is reduced. This is due to the increased distance between the particles that becomes much higher than EDL thickness. For smaller particles (P12%) the flow rate is lower due to the lower distance between obstructions and EDL overlapping. The average velocity achievable in such microchannels is very small. This effect is shown in Fig. 12, where the EDL potential and horizontal velocity distributions are shown for a microchannel 60 $\mu \text{m}$ in width. It appears that the decrease in particle to channel size ratio has a profound effect on flow rate. In particular a reduction in this quantity appears to reduce flow rate.

Fig. 12

Contours of internal potential (a) and horizontal velocity (b), for microchannel with obstructions P12% and $60\,\upmu \text{m}$ in width

3.5 Effect of porosity on EOF

Finally, the influence of effective porosity on EOF is examined. Figure 13 shows the effect of porosity on flow enhancement when channel width is varied. The analysis is carried out in a high porosity range, from 0.4 to 0.8, since the results are finalised to be used for energy applications (Wang 2012). As seen a decrease in the porosity from 0.8 to 0.4 increases the channel width range in which EO flow is enhanced. While flow has come to a stand still at a channel width of $240\,\mu \text{m}$ when a porosity of 0.8 was employed, a finite flow rate is maintained at a porosity value of 0.6 and 0.4. It is also easy to notice that the flow pattern is approaching that of a channel with no obstructions when porosity is increased from 0.4 to 0.8. The effect of porosity largely confirms previous findings. As expected, in narrower channels the effect of overlapping EDL is more evident than in those characterised by a higher porosity, as highlighted in Fig. 14.

Fig. 13

Flow rate variations at two different porosity values for different channel widths

Fig. 14

Contours of internal potential for microchannel with an effective porosity equal to 0.6 (a) and (b), and 0.4 (c) and (d), at different widths: $60\,\upmu \text{m}$ (on the left) and $150\,\upmu \text{m}$ (on the right)

4 Concluding remarks

Electro-osmotic flow through microchannels with and without obstructions has been investigated. For modelling the flow through microchannels with obstructions, an equivalent reference length is introduced to represent the effect of obstructions. The model developed has been used to investigate the effectiveness of introducing flow obstructions in microchannels on enhancing electro-osmotic flow. The results show that beyond a channel width of $100\,\upmu \text{m}$, introducing obstructions increases the effectiveness of electro-osmotic flow-driven systems. The results indicate that obstruction size affects the electro-osmotic flow and that an appropriate compromise between obstruction diameter and their distribution can be found in order to maximise flow rate. Finally, for larger microchannels, increasing the porosity decreases the flow rate. Thus, a decrease in porosity is recommended as the channel width is increased. The results of this study clearly show that the use of obstructions leads to flow enhancement in electro-osmotic systems for most cases analysed.

Appendix: Numerical solution strategy

Both the Laplace and Poisson–Boltzmann equations are solved explicitly, by adding a pseudo-time term which becomes negligible when a steady-state solution is reached.

• Laplace equation

$$\frac{\partial \phi }{\partial t} + \sigma \frac{\partial ^2\phi }{\partial x^2_i} = 0$$

(24)

• Poisson–Boltzmann equation

$$\frac{\partial \psi }{\partial t} + \frac{\partial ^2\psi }{\partial x^2_i} = -\left( \kappa a\right) ^2 \sinh \left( \psi \right)$$

(25)

The above equations are temporally discretised using a forward difference approach and spatially discretised through the standard Galerkin finite element method. The solution of Laplace and Poisson–Boltzmann equations is implemented into the source term of the momentum equation. The modified incompressible Navier–Stokes equations are solved by using the characteristic-based split (CBS) algorithm that consists in splitting the solution into three steps:

• 1. solution to the momentum equation without considering pressure term, introducing an intermediate velocity

• 2. calculation of the pressure

• 3. correction of the velocity

The resulting set of PDEs is then discretised in time by using a characteristic approach as it is described in the following subsections.

1.1 Temporal discretisation: CBS algorithm

In step 1, an intermediate velocity, ${\tilde{u}}$, is calculated after neglecting the pressure term.

$$\begin{aligned} {\tilde{u}}_i -u^n_i =&\, \Delta t \left[ -u_j \frac{\partial u_i}{\partial x_j} + \frac{1}{Re} \frac{\partial ^2 u_i}{\partial {x_i}^2} + J \sinh \left( \psi \right) \left( \frac{\partial \phi }{\partial {x_i}}\right) \right. \\&\left. +\, \frac{\Delta t}{2} u_k \frac{\partial }{\partial x_k} \left( u_j \frac{\partial u_i}{\partial x_j} - \frac{1}{Re} \frac{\partial ^2 u_i}{\partial {x_i}^2} + J \sinh \left( \psi \right) \left( \frac{\partial \phi }{\partial {x_i}}\right) \right) \right] ^n \end{aligned}$$

(26)

At step 2 the pressure is determined as follows

$$\left( \frac{1}{\beta ^2}\right) ^n \left( p^{n+1}-p^n\right) = - \Delta t \frac{\partial u^{n+\theta _1}_i}{\partial x_i}$$

(27)

and it is used to correct the momentum in step 3 as

$$u^{n+1}_i -{\tilde{u}}_i = \Delta t \frac{\partial p^{n+\theta _2}}{\partial x_i} + \frac{\Delta t^2}{2} u^n_k \frac{\partial ^2 p^n}{\partial x_k \partial x_i}$$

(28)

Substituting $u^{n+1}$ from (27) into Eq. (26), the final temporally discrete form of the pressure equation is obtained as

$$\begin{aligned} \left( \frac{1}{\beta ^2}\right) ^n \left( p^{n+1}-p^n\right) =&- \Delta t \left[ \theta _1 \frac{\partial {\tilde{u}}_i}{\partial x_i} + \left( 1-\theta _1\right) \frac{\partial u^n_i}{\partial x_i} \right] \\&+ \Delta t \theta _1 \frac{\partial }{\partial x_i} \left[ \theta _2 \frac{\partial p^{n+1}_i}{\partial x_i} + \left( 1-\theta _2\right) \frac{\partial p^n_i}{\partial x_i} - \frac{\Delta t}{2} u_k \frac{\partial }{\partial x_k} \left( \frac{\partial p^n_i}{\partial x_i}\right) \right] \end{aligned}$$

(29)

where $0.5<\theta <1.0$ and $\theta _2=0$ for a fully explicit scheme.

1.2 Spatial discretisation

The above equations are spatially discretised using the Galerkin finite element procedure and the following spatial discretisation of the variables.

$${\tilde{u}}_i = \sum ^m_{a=1} N^a \overline{{\tilde{u}}}^{a}_i;\qquad u_i = \sum ^m_{a=1} N^a {\overline{u}}^a_i;\qquad p = \sum ^m_{a=1} N^a {\overline{p}}^a;$$

where the overline indicates the nodal value, m is the number of nodes in the element, and a represents a specific node. After spatial discretisation the equations are weighted through the shape functions, N, and then integrated over the whole domain.

The final matrix forms of the spatially discretised equations may be written as:

• Step 1

  $${\mathbf {M}} \Delta \overline{{\tilde{u}}}_i = - \Delta t \left[ {\mathbf {C}} {\overline{u}}_i + {\mathbf {K}}_{\tau i} + {\mathbf {F}}_i\right] + \frac{\Delta t}{2} \left[ {\mathbf {K}}_u {\overline{u}}_i\right] + f_{\tau i}$$

  (30)

  where

  $$\begin{aligned} {\mathbf {M}}\equiv & {} \int _\Omega {\mathbf {N}}^T{\mathbf {N}}\text{d}\Omega ; \qquad {\mathbf {C}} \equiv \int _\Omega {\mathbf {N}}^T \frac{\partial }{\partial x_j} {\mathbf {N}} u_j \text{d}\Omega ;\\ {\mathbf {K}}_{\tau i}\equiv & {} \int _\Omega {\mathbf {N}}^T \frac{\partial }{\partial x_j} \tau _{ij}\text{d}\Omega ; \qquad {\mathbf {F}}_i \equiv \int _\Omega {\mathbf {N}}^T J \sinh \left( \psi \right) \frac{\partial {\mathbf {N}}}{\partial {x_i}}\phi \text{d}\Omega ;\\ {\mathbf {K}}_u\equiv & {} \int _\Omega {\mathbf {N}}^T u_k \frac{\partial }{\partial x_k} \left( \frac{\partial }{\partial x_j} {\mathbf {N}} u_j \right) \text{d}\Omega ; \qquad f_{\tau i} \equiv \int _\Gamma {\mathbf {N}}^T \tau _{ij}n_j \text{d}\Gamma ; \end{aligned}$$

• Step 2

  $$\left( {\mathbf {B}} + \Delta t^2 \theta _1 \theta _2 {\mathbf {H}} \right) \Delta {\overline{p}} = \Delta t \left[ {\mathbf {G}} {\overline{u}}^n_i + \theta _1 {\mathbf {G}} \Delta \overline{{\tilde{u}}}_i - \Delta t \theta _1\ {\mathbf {H}} {\overline{p}}^n - f_p\right]$$

  (31)

  where

  $$\begin{aligned} {\mathbf {B}}\equiv & {} \int _\Omega {\mathbf {N}}^T \frac{1}{\beta ^2} {\mathbf {N}}\text{d}\Omega ;\qquad {\mathbf {H}} \equiv \int _\Omega \frac{\partial {\mathbf {N}}^T }{\partial x_i} \frac{\partial {\mathbf {N}}}{\partial x_i} \text{d}\Omega ;\\ {\mathbf {G}}\equiv & {} \int _\Omega \frac{\partial {\mathbf {N}}^T }{\partial x_i} {\mathbf {N}} \text{d}\Omega ;\\ {\mathbf {f}}_p\equiv & {} \Delta t \int _\Gamma {\mathbf {N}}^T \left[ {\overline{u}}^n_i + \theta _1\left( \Delta \overline{{\tilde{u}}}_i - \Delta t \frac{\partial p^{n+\theta _2}}{\partial x_i}\right) \right] n^T_i \text{d}\Gamma ; \end{aligned}$$

• Step 3

  $$\Delta {\overline{u}}_i = \Delta \overline{{\tilde{u}}}_i + {\mathbf {M}}^{-1} \Delta t \left[ {\mathbf {G}} \left( {\overline{p}}^n + \theta _2 \Delta {\overline{p}}\right) - \frac{\Delta t}{2} {\mathbf {L}} {\overline{p}}^n\right]$$

  (32)

  where

  $${\mathbf {L}} \equiv \int _\Omega \frac{\partial }{\partial x_i} {\mathbf {N}}^T u_i \frac{\partial {\mathbf {N}}}{\partial x_j} \text{d}\Omega ;$$