Effect of solvent polarization on electroosmotic transport in a nanofluidic channel

Abstract

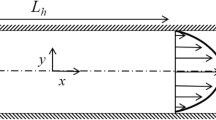
In this paper, we develop a theory based on the Langevin–Bikerman approach to study the electroosmotic (EOS) transport in a nanofluidic channel in the presence of finite solvent polarization effect (SPE). At the outset, we conduct an analysis based on practically achievable parameters to highlight the consequence of SPE in the variation in the electric double-layer (EDL) electrostatics. We witness that SPE invariably increases the effective EDL thickness; our numerical results are justified through a scaling analysis. More importantly, we unravel that the EOS transport, most remarkably, shows negligible influence on the qualitative variation in the EDL electrostatic potential; rather, it is dictated by the ratio of the effective to the actual EDL thicknesses. This finding, supported by scaling analysis, ensures that for the chosen set of parameters, SPE invariably enhances the EOS transport. Apart from shedding light on this extremely non-intuitive nanoscopic electroosmotic flow phenomenon, we anticipate that the present study will embolden us to better control the nanofluidic transport for a plethora of biological and industrial applications.

Appendix: Nomenclature

Symbol	Definition	Symbol	Definition
h	Channel half height	E	Axial electric field
$\lambda$	EDL thickness	$\psi$	EDL electrostatic potential
${\mathcal {F}}$	Free energy	f	Free energy density
y	Transverse direction	$\epsilon _0$	Permittivity of free space
e	Electronic charge	$\epsilon _r$	Relative permittivity of liquid
$k_B$	Boltzmann constant	T	Temperature in K
$n_s$	Number density of lattice sites	$n_0$	Bulk number density of ions
$n_+$	Number density of cations	$n_-$	Number density of anions
$n_w$	Number density of water molecules	$n_{0w}$	Bulk number density of water molecules
$p_0$	Dipole moment of water	$\alpha$	Lagrange multiplier
$\bar{\psi }$	$e\psi /k_B T$	$\bar{y}$	y / h
$\bar{\lambda }$	$\lambda /h$	$\bar{n}_{\pm }$	$n_{\pm }/n_0$
${\mathcal {L}}$	Langevin function	$\zeta$	Zeta potential
u	Velocity	$\bar{\zeta }$	$e\zeta /k_B T$
$\eta$	Dynamic viscosity	$E_0$	$k_B T/e h$
$u_0$	$\epsilon _0 \epsilon _r k_B T E_0/(e \eta )$ (velocity scale)	A	$p_0/eh$ (dimensionless solvent polarization number)
$\bar{u}$	$u/u_0$	$\bar{E}$	$E/E_0$
B	$n_{0w}/n_0$ (dimensionless bulk water number density)	$\bar{\lambda }_{\mathrm{eff}}$	$\lambda _{\mathrm{eff}}/h$ (dimensionless effective EDL thickness)