On the conditional superiority of counter-current over co-current extraction in microchannels

Abstract

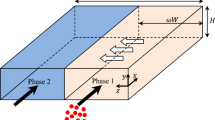
In liquid–liquid extraction, counter-current flow of the phases always results in an improved performance as compared to co-current flow, under similar operating conditions. However, it is challenging to implement counter-current flow in a microchannel. Therefore, the improvement in extraction performance must be significant to justify the selection of counter-current flow over co-current flow in microchannels. In this study, we identify the range of fluid properties and operating conditions for which counter-current operation exhibits significant benefits. For this, simplified mathematical models are developed for both co-current and counter-current extraction in the stratified flow regime. These models, while being simple, capture the essential physics of the extraction process and facilitate a thorough investigation of the relative extraction performance across the parameter space. An analytical solution, based on the theory of Sturm–Liouville linear operators, is obtained for the case of co-current flow. The counter-current model belongs to the class of two-way diffusion equations for which a novel semi-analytical solution is presented. The analysis of the predictions of the models shows that the relative extraction performance is governed by a general principle of maximum gain at mediocre performance. These results help identify the significantly restricted range of operating parameters for which counter-current operation is a truly attractive alternative to the co-current mode of extraction in microchannels.

Appendix: analytical solution of the co-current model

The details of the solution of the co-current concentration field are given in this appendix. Here the solution is presented within the framework of linear operator theory. Entirely equivalent results may be obtained by the well-known ‘separation of variables’ method of solution.

Equation (9) may be represented concisely in linear operator form as

$$- \frac{{{\text{d}}c}}{{{\text{d}}x}} = Lc $$

(39)

Here L is a Sturm–Liouville operator defined on the Hilbert Space $\cal{L}[\text{0,1}]$

$$Lc = - \frac{1}{{v_{\text{r}} (y)}}\frac{\text{d}}{{{\text{d}}y}}\left[ {\frac{1}{\text{Pe}}\frac{{{\text{d}}c}}{{{\text{d}}y}}} \right]\quad 0 < y < 1 $$

(40)

where c(y) is a piecewise continuous function. It is continuous everywhere except at the interface. v _r(y) and Pe are piecewise constant functions given by

$$\begin{array}{*{20}c} {\begin{array}{*{20}c} {{\text{Pe}} = {\text{Pe}}_{1} ,} \\ {{\text{Pe}} = {\text{Pe}}_{2} ,} \\ \end{array} } & {\begin{array}{*{20}c} {v_{\text{r}} = 1} \\ {v_{\text{r}} = \left( {{{v_{2} } \mathord{\left/ {\vphantom {{v_{2} } {v_{1} }}} \right. \kern-0pt} {v_{1} }}} \right)} \\ \end{array} } & {\left\{ {\begin{array}{*{20}c} {0 < y < h_{\text{r}} } \\ {h_{\text{r}} < y < 1} \\ \end{array} } \right.} \\ \end{array} $$

(41)

Following the treatment of Ramkrishna and Amundson (1974), we define an inner product which renders the operator L self-adjoint.

$$\left\langle {f,g} \right\rangle = \int\limits_{0}^{{h_{\text{r}} }} {f_{1} (y)g_{1} (y){\text{d}}y} + K\left( {{{v_{2} } \mathord{\left/ {\vphantom {{v_{2} } {v_{1} }}} \right. \kern-0pt} {v_{1} }}} \right)\int\limits_{{h_{\text{r}} }}^{1} {f_{2} (y)g_{2} (y){\text{d}}y} $$

(42)

In this inner product, it can be seen that L is self-adjoint, i.e., it satisfies

$$\left\langle {Lf,g} \right\rangle = \left\langle {f,Lg} \right\rangle $$

(43)

Such a self-adjoint operator on the Hilbert space $\cal{L}[\text{0,1}]$ can be shown to possess a discrete spectrum of eigen values. The corresponding eigen functions form an orthonormal basis (Ramkrishna and Amundson 1974, 1985). Thus, we can represent the solution as

$$c(x,y) = \sum\limits_{n} {\left\langle {c,\phi_{n} (y)} \right\rangle \phi_{n} (y)} $$

(44)

where ϕ _n (y) is the nth orthonormal eigen function. The eigen functions are also piecewise continuous with a single point of discontinuity at the interface. The eigen value problem is given by

$$L\phi_{n} = \lambda_{n}^{2} \phi_{n} $$

(45)

The eigen values of the operator L are non-negative. This fact is made explicit by representing them as $\lambda_{n}^{2}$. The coefficients of the eigen functions in Eq. (44) are obtained by taking the inner product of Eq. (39) with ϕ _n (y) and applying Eq. (45).

$$- \frac{{{\text{d}}\left\langle {c,\phi_{n} (y)} \right\rangle }}{{{\text{d}}x}} = \left\langle {Lc,\phi_{n} (y)} \right\rangle = \left\langle {c,L\phi_{n} (y)} \right\rangle = \lambda_{n}^{2} \left\langle {c,\phi_{n} (y)} \right\rangle $$

(46)

On solving this ordinary differential equation and substituting the result in Eq. (44), we obtain the infinite series solution as

$$c(x,y) = \sum\limits_{n} {\left\langle {c(0,y),\phi_{n} (y)} \right\rangle e^{{ - \lambda_{n}^{2} x}} \phi_{n} (y)} $$

(47)

The eigen values and eigen functions are obtained by solving the eigen value problem of Eq. (45). The general solution to Eq. (45) is

$$\begin{aligned}&{\phi_{1,n} (y) = A\sin \left( {\lambda_{n} \sqrt {{\text{Pe}}_{1} } y} \right) + B\cos \left( {\lambda_{n} \sqrt {{\text{Pe}}_{1} } y} \right)}\quad {0 < y < h_{\text{r}} } \\ &{\phi_{2,n} (y) = C\sin \left( {\lambda_{n} \sqrt {{\text{Pe}}_{2} \left( {{{v_{2} } \mathord{\left/ {\vphantom {{v_{2} } {v_{1} }}} \right. \kern-0pt} {v_{1} }}} \right)} (1 - y)} \right) + D\cos \left( {\lambda_{n} \sqrt {{\text{Pe}}_{2} \left( {{{v_{2} } \mathord{\left/ {\vphantom {{v_{2} } {v_{1} }}} \right. \kern-0pt} {v_{1} }}} \right)} (1 - y)} \right)} \quad {h_{\text{r}} < y < 1} \\ \end{aligned}$$

(48)

Here $\lambda_{n}^{{}}$ is the positive root of $\lambda_{n}^{2}$. The no-flux boundary conditions in Eq. (10) require that A = C = 0. The boundary conditions at the interface give rise to a set of two homogeneous linear algebraic equations. For non-trivial solutions to Eq. (45), the determinant of this system of equations must vanish. This yields the characteristic equation which determines the eigen values.

$$\begin{gathered} \sqrt {{\text{Pe}}_{2} \left( {{{v_{2} } \mathord{\left/ {\vphantom {{v_{2} } {v_{1} }}} \right. \kern-0pt} {v_{1} }}} \right)} \cos \left( {\lambda_{n} \sqrt {{\text{Pe}}_{1} } h_{\text{r}} } \right)\sin \left( {\lambda_{n} \sqrt {{\text{Pe}}_{2} \left( {{{v_{2} } \mathord{\left/ {\vphantom {{v_{2} } {v_{1} }}} \right. \kern-0pt} {v_{1} }}} \right)} \left( {1 - h_{\text{r}} } \right)} \right) \hfill \\ \quad + K\beta \sqrt {{\text{Pe}}_{1} } \sin \left( {\lambda_{n} \sqrt {{\text{Pe}}_{1} } h_{\text{r}} } \right)\cos \left( {\lambda_{n} \sqrt {{\text{Pe}}_{2} \left( {{{v_{2} } \mathord{\left/ {\vphantom {{v_{2} } {v_{1} }}} \right. \kern-0pt} {v_{1} }}} \right)} \left( {1 - h_{\text{r}} } \right)} \right) = 0 \hfill \\ \end{gathered} $$

(49)

Equation (44) is transcendental in $\lambda_{n}^{{}}$ and must be solved numerically. Care should be taken to insure that all eigen values are obtained. Further, they must be paired correctly with the corresponding eigen functions in the series solution. The eigen functions are given by

$$\phi_{n} (y) = \left\{ {\begin{array}{ll} {\phi_{1,n} (y) = b_{n} \cos \left( {\lambda_{n} \sqrt {{\text{Pe}}_{1} } y} \right)} & {0 < y < h_{\text{r}} } \\ {\phi_{2,n} (y) = d_{n} \cos \left( {\lambda_{n} \sqrt {{\text{Pe}}_{2} \left( {{{v_{2} } \mathord{\left/ {\vphantom {{v_{2} } {v_{1} }}} \right. \kern-0pt} {v_{1} }}} \right)} \left( {1 - y} \right)} \right)} & {h_{\text{r}} < y < 1} \\ \end{array} } \right.$$

(50)

where b _n and d _n are evaluated to insure orthonormality of the eigen functions according to the definition of the inner product in Eq. (42).

$$\begin{aligned} b_{n} &=\left[ {\frac{{2\lambda_{n} \sqrt {{\text{Pe}}_{1} } h_{\text{r}} + \sin \left( {2\lambda_{n} \sqrt {{\text{Pe}}_{1} } h_{\text{r}} } \right)}}{{4\lambda_{n} \sqrt {{\text{Pe}}_{1} } }} + \left\{ {K\beta^{2} \frac{{{\text{Pe}}_{1} }}{{{\text{Pe}}_{2} }}\frac{{\sin^{2} \left( {\lambda_{n} \sqrt {{\text{Pe}}_{1} } h_{\text{r}} } \right)}}{{\sin^{2} \left( {\lambda_{n} \sqrt {{\text{Pe}}_{2} \left( {{{v_{2} } \mathord{\left/ {\vphantom {{v_{2} } {v_{1} }}} \right. \kern-0pt} {v_{1} }}} \right)} \left( {1 - h_{\text{r}} } \right)} \right)}}} \right.} \right. \\ &\quad \left. {\left. { \times \frac{{2\left( {1 - h_{\text{r}} } \right)\lambda_{n} \sqrt {{\text{Pe}}_{2} \left( {{{v_{2} } \mathord{\left/ {\vphantom {{v_{2} } {v_{1} }}} \right. \kern-0pt} {v_{1} }}} \right)} + \sin \left( {2\lambda_{n} \sqrt {{\text{Pe}}_{2} \left( {{{v_{2} } \mathord{\left/ {\vphantom {{v_{2} } {v_{1} }}} \right. \kern-0pt} {v_{1} }}} \right)} \left( {1 - h_{\text{r}} } \right)} \right)}}{{4\lambda_{n} \sqrt {{\text{Pe}}_{2} \left( {{{v_{2} } \mathord{\left/ {\vphantom {{v_{2} } {v_{1} }}} \right. \kern-0pt} {v_{1} }}} \right)} }}} \right\}} \right]^{{ - {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} \\ \end{aligned} $$

(51)

$$d_{n} = - b_{n} \beta \frac{{\sqrt {{\text{Pe}}_{1} } }}{{\sqrt {{\text{Pe}}_{2} \left( {{{v_{2} } \mathord{\left/ {\vphantom {{v_{2} } {v_{1} }}} \right. \kern-0pt} {v_{1} }}} \right)} }}\frac{{\sin \left( {\lambda_{n} \sqrt {{\text{Pe}}_{1} } h_{\text{r}} } \right)}}{{\sin \left( {\lambda_{n} \sqrt {{\text{Pe}}_{2} \left( {{{v_{2} } \mathord{\left/ {\vphantom {{v_{2} } {v_{1} }}} \right. \kern-0pt} {v_{1} }}} \right)} \left( {1 - h_{\text{r}} } \right)} \right)}} $$

(52)

Equation (49) admits a zero eigen value. The corresponding eigen function is

$$\phi_{0} (y) = \left\{ {\begin{array}{ll} {\phi_{1,0} (y) = \frac{1}{{\sqrt {h_{\text{r}} + \left( {{{v_{2} } \mathord{\left/ {\vphantom {{v_{2} } {v_{1} }}} \right. \kern-0pt} {v_{1} }}} \right)\frac{{\left( {1 - h_{\text{r}} } \right)}}{K}} }}} & {0 < y < h_{\text{r}} } \\ {\phi_{1,0} (y) = \frac{1}{K}\phi_{1,0} (y)} & {h_{\text{r}} < y < 1} \\ \end{array} } \right.$$

(53)

Substituting Eqs. (50)–(53) in Eq. (47), one obtains the solution as given in Eq. (14).