Skip to main content

Advertisement

SpringerLink
Log in

Collapse of micrometer-sized cavitation bubbles near a rigid boundary

  • Research Paper
  • Published:
Microfluidics and Nanofluidics Aims and scope Submit manuscript

Abstract

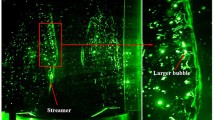
The interaction of cavitation bubbles with a rigid boundary and its dependence on the distance between bubble and boundary is investigated experimentally. Individual cavitation bubbles, with a maximum radius of 150 μm, are generated by using pulsed high-intensity focused ultrasound. Observations are made with high-speed photography with framing rates of up to 200 million frames per second and exposure time of 5 ns, and the spatial resolution is in the order of a few micrometers. The significant parameter of this study is the non-dimensional stand-off parameter, γ, defined as the distance between the ultrasound focus and the rigid boundary scaled by the maximum bubble radius. Both the velocity of the liquid jet developed during bubble collapse and the maximum pressure of the shock wave emitted during bubble rebound show a minimum for γ ≈ 1 and a constant value for γ > 3. The maximum jet velocity is slightly smaller than the corresponding values obtained in the case of millimeter-sized bubbles and ranges from 80 m/s (at γ ≈ 1) to 130 m/s (for γ > 3). No jet formation was observed for γ > 3. The shock wave pressure, measured at a distance of 5 mm from the emission center, ranges from 0.2 MPa (at γ ≈ 1) to 0.65 MPa (for γ > 3). These values are an order of magnitude smaller than those obtained in the case of millimeter-sized bubbles. The shock wave duration is almost independent of γ at a value of about 75 ns. For large γ values (γ > 3), a large percentage of the bubble energy (up to 60 %) is transformed into the mechanical energy of the shock wave emitted during bubble rebound but, for γ ≈ 1, the conversion efficiency decreases to 30 %. Independent of the relative distance between bubble and rigid boundary, the shock pressure decays proportionally to r −1 with increasing distance r from the emission center. The results are discussed with respect to cavitation damage and collateral effects in pulsed high-intensity focused ultrasound surgery.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  • Ali AM, Raj NAN (2008) Tensile, flexural and compressive strength studies on natural and artificial phosphate urinary stones. Urol Res 36:289–295

    Article  Google Scholar 

  • Benjamin TB, Ellis AT (1966) The collapse of cavitation bubbles and the pressure thereby produced against solid boundaries. Phil Trans R Soc Lond A 260:221–240

    Article  Google Scholar 

  • Blake JR, Gibson DC (1987) Cavitation bubbles near boundaries. Annu Rev Fluid Mech 19:99–123

    Article  Google Scholar 

  • Blake JR, Hooton MC, Robinson PB, Tong RP (1997) Collapsing cavities, toroidal bubbles and jet impact. Phil Trans Roy Soc 355:537–550

    Article  MathSciNet  MATH  Google Scholar 

  • Boal D (2002) Mechanics of the cell. Cambridge University Press, Cambridge

    Google Scholar 

  • Brujan EA (2008) Shock wave emission from laser-induced cavitation bubbles in polymer solutions. Ultrasonics 48:423–426

    Article  Google Scholar 

  • Brujan EA (2009) Cardiovascular cavitation. Med Eng Phys 31:742–751

    Article  Google Scholar 

  • Brujan EA, Vogel A (2006) Stress wave emission and cavitation bubble dynamics by nanosecond optical breakdown in a tissue phantom. J Fluid Mech 558:281–308

    Article  MATH  Google Scholar 

  • Brujan EA, Nahen K, Schmidt P, Vogel A (2001) Dynamics of laser-induced cavitation bubbles near elastic boundaries: influence of the elastic modulus. J Fluid Mech 433:283–314

    MATH  Google Scholar 

  • Brujan EA, Keen GS, Vogel A, Blake JR (2002) The final stage of the collapse of a cavitation bubble close to rigid boundary. Phys Fluids 14:85–92

    Article  Google Scholar 

  • Brujan EA, Ikeda T, Matsumoto Y (2008) On the pressure of cavitation bubbles. Exp Therm Fluid Sci 32:1188–1191

    Article  Google Scholar 

  • Brunton JH (1966) High speed liquid impact. Phil Trans R Soc Lond A 260:79–85

    Article  Google Scholar 

  • Burns JR, Shoemaker BE, Gauthier JF, Finlayson B (1985) Hardness testing of urinary calculi. In: Schwille PO, Smith LH, Robertson WG, Vahlensieck W (eds) Urolithiasis and related clinical research. Plenum, New York, pp 181–185

    Google Scholar 

  • Chartier-Kastler E, Yonneau L, Conort P, Haertig A, Bitker MO, Richard F (2000) High intensity focused ultrasound (HIFU) in urology. Prog Urol 10:1108–1117

    Google Scholar 

  • Cole RH (1948) Underwater explosions. Princeton University Press, Princeton

    Google Scholar 

  • Feng ZC, Leal LG (1997) Nonlinear bubble dynamics. Annu Rev Fluid Mech 29:201–243

    Article  MathSciNet  Google Scholar 

  • Kornfeld M, Suvorov L (1944) On the destructive action of cavitation. J Appl Phys 15:495–506

    Article  Google Scholar 

  • Krasokha N, Theisen W, Reese S, Mordasini P, Brekenfeld C, Gralla J, Slotboom J, Schrott G, Monstadt H (2010) Mechanical properties of blood clots—a new test method. Mat wiss u Werkstofftech 41:1019–1024

    Article  Google Scholar 

  • Kuznetsova TG, Starodubtseva MN, Yegorenkov NI, Chizhik SA, Zhdanov RI (2007) Atomic force microscopy probing of cell elasticity. Micron 38:824–833

    Article  Google Scholar 

  • Lauterborn W (1974) Kavitation durch laserlicht. Acustica 31:51–78

    Google Scholar 

  • Lauterborn W, Bolle H (1975) Experimental investigations of cavitation bubble collapse in the neighbourhood of a solid boundary. J Fluid Mech 72:391–399

    Article  Google Scholar 

  • Lauterborn W, Kurz T (2010) Physics of bubble oscillations. Rep Prog Phys 73:106501

    Article  Google Scholar 

  • Lauterborn W, Kurz T, Schenke C, Lindau O, Wolfrum B (2001) Laser-induced bubbles in cavitation research. In: IUTAM symposium in free surface flows. Kluwer, Dordrecht, pp 169–176

  • Leslie TA, Kennedy JE (2006) High-intensity focused ultrasound principles, current uses, and potential for the future. Ultrasound Quart 22:263–272

    Article  Google Scholar 

  • Lesser MB, Field JE (1983) The impact of compressible liquids. Ann Rev Fluid Mech 15:97–122

    Article  Google Scholar 

  • Lindau O, Lauterborn W (2003) Cinematographic observation of the collapse and rebound of a laser-produced cavitation bubble near a wall. J Fluid Mech 479:327–348

    Article  MATH  Google Scholar 

  • Lush PA (1983) Impact of a liquid mass on a perfectly plastic solid. J Fluid Mech 135:373–387

    Article  MATH  Google Scholar 

  • Murata S, Watanabe H, Takahashi T, Watanabe K, Oinuma S (1977) Studies on the application of microexplosion to medicine and biology. II. Construction and strength of urinary calculi. Jpn J Urol 68:249–256

    Google Scholar 

  • Naudé CF, Ellis AT (1961) On the mechanism of cavitation damage by non-hemispherical cavities collapsing in contact with a solid boundary. Trans ASME D J Basic Eng 83:648–656

    Article  Google Scholar 

  • Obreschkow D, Tinguely M, Dorsaz N, Kobel P, de Bosset A, Farhat M (2011) Universal scaling law for jets of collapsing bubbles. Phys Rev Lett 107:204501

    Article  Google Scholar 

  • Pearson A, Blake JR, Otto SR (2004) Jets in bubbles. J Eng Math 48:391–412

    Article  MathSciNet  MATH  Google Scholar 

  • Philipp A, Lauterborn W (1998) Cavitation erosion by single laser-produced bubbles. J Fluid Mech 361:75–116

    Article  MATH  Google Scholar 

  • Popinet S, Zaleski S (2002) Bubble collapse near a solid boundary: a numerical study of the influence of viscosity. J Fluid Mech 464:137–163

    Article  MATH  Google Scholar 

  • Rayleigh L (1917) On the pressure developed in a liquid during the collapse of a spherical cavity. Philos Mag 34:94–98

    Article  MATH  Google Scholar 

  • Roberts WW, Hall TL, Ives K, Wolf JS, Fowlkes JB, Cain CA (2006) Pulsed cavitational ultrasound: a noninvasive technology for controlled tissue ablation (histotripsy) in the rabbit kidney. J Urol 175:734–738

    Article  Google Scholar 

  • Samiei E, Shams M, Ebrahimi R (2011) A novel numerical scheme for the investigation of surface tension effects on growth and collapse stages of cavitation bubbles. Eur J Mech B Fluids 30:41–50

    Article  MATH  Google Scholar 

  • Shima A, Takayama K, Tomita Y, Miura N (1981) An experimental study on effects of a solid wall on the motion of bubbles and shock waves in bubble collapse. Acustica 48:293–301

    Google Scholar 

  • Tomita Y, Shima A (1986) Mechanisms of impulsive pressure generation and damage pit formation by bubble collapse. J Fluid Mech 169:535–564

    Article  Google Scholar 

  • Tong RP, Schiffers WP, Shaw SJ, Blake JR, Emmony DC (1999) The role of “splashing” in the collapse of a laser-generated cavity near a rigid boundary. J Fluid Mech 380:339–361

    Article  MATH  Google Scholar 

  • Vogel A (1997) Non-linear absorption: intraocular microsurgery and laser lithotripsy. Phys Med Biol 42:895–912

    Article  Google Scholar 

  • Vogel A, Lauterborn W (1988) Acoustic transient generation by laser-produced cavitation bubbles near solid boundaries. J Acoust Soc Am 84:719–731

    Article  Google Scholar 

  • Vogel A, Venugopalan V (2003) Mechanisms of pulsed laser ablation of biological tissues. Chem Rev 103:577–644

    Article  Google Scholar 

  • Vogel A, Lauterborn W, Timm R (1989) Optical and acoustic investigations of the dynamics of laser-produced cavitation bubbles near a solid boundary. J Fluid Mech 206:299–338

    Article  Google Scholar 

  • Vogel A, Noack J, Nahen K, Theisen D, Busch S, Parlitz U, Hammer DX, Noojin GD, Rockwell BA, Birngruber R (1999) Energy balance of optical breakdown in water at nanosecond to femtosecond time scales. Appl Phys B 68:271–280

    Article  Google Scholar 

  • Wang SJ, Yip MC (2002) The modulus and toughness of urinary calculi. J Biomech Eng 24:133–134

    Article  Google Scholar 

Download references

Acknowledgments

This work was supported by a grant of the Romanian National Authority for Scientific Research, CNCS–UEFISCDI, project number PN-II-ID-PCE-2011-3-0079, and by the Japan Society for the Promotion of Science, Grant S-07189. We thank T. Ikeda for his help with the experiments.

Author information

Authors and Affiliations

  1. Department of Hydraulics, University Politehnica Bucharest, Spl. Independentei 313, 060042, Bucharest, Romania

    Emil-Alexandru Brujan

  2. Department of Mechanical Engineering, The University of Tokyo, 7-3-1 Hongo, Bunkyo, Tokyo, 113-8656, Japan

    Yoichiro Matsumoto

Authors
  1. Emil-Alexandru Brujan
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yoichiro Matsumoto
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Emil-Alexandru Brujan.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Brujan, EA., Matsumoto, Y. Collapse of micrometer-sized cavitation bubbles near a rigid boundary. Microfluid Nanofluid 13, 957–966 (2012). https://doi.org/10.1007/s10404-012-1015-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10404-012-1015-6

Keywords

Search

Navigation