Eccentric electrophoretic motion of a sphere in circular cylindrical microchannels

Abstract

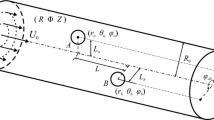
The eccentric electrophoretic motion of a spherical particle in an aqueous electrolyte solution in circular cylindrical microchannels is studied in this paper. The objective is to investigate the influences of separation distance and channel size on particle motion. A theoretical model is developed to describe the electric field, the flow field and the particle motion. A finite element based direct numerical simulation method is employed to solve the model. Numerical results show that, when the particle is eccentrically positioned in the channel, the electric field and the flow field are not symmetric, and the strongest electric field and the highest flow velocity occur in the small gap region. It is shown that the rotational velocity of the particle increases with the decrease of the separation distance. With the decrease of the separation distance, the translational velocity increases in a smaller channel; while it decreases first and then increases in a relatively large channel. When a particle moves eccentrically at a smaller separation distance from the channel wall, both the translational velocity and the rotational velocity increase with the decrease of the channel size.