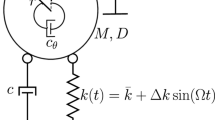Abstract
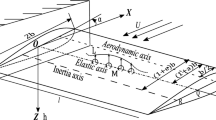
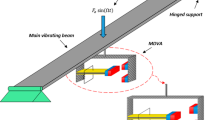
Beam structures are extensively used in many engineering branches. For marine engineering, the ship shafting system is generally simplified as a vibration model with single or multiple beam structures connected by the coupling stiffness. In engineering, multiple nonlinear energy sinks (NESs) can be arranged on the premise of sufficient installation space to ensure their vibration suppression effect. Considering engineering practice, this study investigates the dynamic behavior and vibration suppression of a generally restrained pre-pressure beam structure with multiple uniformly distributed NESs, where the pre-pressure is typically caused by thrust bearings, installation ways, and others. System governing equations are derived through the generalized Hamiltonian principle and the variational procedure. Dynamic responses of the pre-pressure beam structure are predicted by the Galerkin truncation method. The effect of NESs on dynamic responses and vibration suppression of the pre-pressure beam structure is studied and discussed. Suitable parameters of NESs have a beneficial effect on the vibration suppression at both ends of the pre-pressure beam structure. NESs can modify the vibration frequency and energy transmission characteristics of the vibration system. For different boundary conditions, the optimized parameters of NESs significantly suppress the vibration energy of the pre-pressure beam structure.
















Similar content being viewed by others
Data Availability
The datasets generated during and/or analyzed during the current study are available from the corresponding author upon reasonable request.
References
Abbas BAH, Irretier H. Experimental and theoretical investigations of the effect of root flexibility on the vibration characteristics of cantilever beams. J Sound Vib. 1989;130(3):353–62.
Register AH. A note on the vibrations of generally restrained, end-loaded beams. J Sound Vib. 1994;172(4):561–71.
Kang KH, Kim KJ. Modal properties of beams and plates on resilient supports with rotational and translational complex stiffness. J Sound Vib. 1996;190(2):207–20.
Wang JTS, Lin CC. Dynamic analysis of generally supported beams using Fourier series. J Sound Vib. 1996;196(3):285–93.
Kim HK, Kim MS. Vibration of beams with generally restrained boundary conditions using Fourier series. J Sound Vib. 2001;245(5):771–84.
Li WL. Free vibrations of beams with general boundary conditions. J Sound Vib. 2000;237(4):709–25.
Wang QS, Shi DY, Liang Q. Free vibration analysis of axially loaded laminated composite beams with general boundary conditions by using a modified Fourier-Ritz approach. J Compos Mater. 2016;50(15):2111–35.
Chen LJ, Xu DS, Du JT, Zhong CW. Flexural vibration analysis of nonuniform double-beam system with general boundary and coupling conditions. Shock Vib. 2018;2018:5103174.
Chen Q, Du JT. A Fourier series solution for the transverse vibration of rotating beams with elastic boundary supports. Appl Acoust. 2019;155:1–15.
Xu DS, Du JT, Tian C. Vibration characteristics and power flow analyses of a ship propulsion shafting system with general support and thrust loading. Shock Vib. 2020;2020:3761590.
Vakakis AF. Inducing passive nonlinear energy sinks in vibrating systems. J Vib Acoust. 2001;123(3):324–32.
Gendelman OV. Transition of energy to a nonlinear localized mode in a highly asymmetric system of two oscillators. Nonlinear Dyn. 2001;25:237–53.
Gendelman O, Manevitch LI, Vakakis AF, Closkey RM. Energy pumping in nonlinear mechanical oscillators: part I—dynamics of the underlying Hamiltonian systems. J Appl Mech. 2001;68(1):34–41.
Vakakis AF, Gendelman O. Energy pumping in nonlinear mechanical oscillators: part II—resonance capture. J Appl Mech. 2001;68(1):42–8.
Jiang XA, Mcfarland DM, Bergman LA, Vakakis AF. Steady state passive nonlinear energy pumping in coupled oscillators: theoretical and experimental results. Nonlinear Dyn. 2003;33:87–102.
Vakakis AF. Designing a linear structure with a local nonlinear attachment for enhanced energy pumping. Meccanica. 2003;38:677–86.
Vakakis AF. Passive nonlinear targeted energy transfer. Phil Trans R Soc A. 2018;376:20170132.
Vakakis AF. Relaxation oscillations, subharmonic orbits and chaos in the dynamics of a linear lattice with a local essentially nonlinear attachment. Nonlinear Dyn. 2010;61:443–63.
Sapsis TP, Quinn DD, Vakakis AF, Bergman LA. Effective stiffening and damping enhancement of structures with strongly nonlinear local attachments. J Vib Acoust. 2012;134(1):011016.
Zhang YW, Lu YN, Zhang W, Teng YY, Yang HX, Yang TZ, Chen LQ. Nonlinear energy sink with inerter. Mech Syst Signal Process. 2018;125(15):52–64.
Zhang J, Zhang YW, Ding H, Yang TZ, Chen LQ. The evaluation of a nonlinear energy sink absorber based on the transmissibility. Mech Syst Signal Process. 2019;125:99–122.
Chen LQ, Li X, Lu ZQ, Zhang YW, Ding H. Dynamic effects of weights on vibration reduction by a nonlinear energy sink moving vertically. J Sound Vib. 2019;451:99–109.
Lee YS, Vakakis AF, Bergman LA, Mcfarland DM, Kerschen G, Nucera F, Tsakirtzis S, Panagopoulos PN. Passive non-linear targeted energy transfer and its applications to vibration absorption: a review. Proc Inst Mech Eng K J Multi-body Dyn. 2008;222(2):77–134.
Gatti G, Brennan MJ, Tang B. Some diverse examples of exploiting the beneficial effects of geometric stiffness nonlinearity. Mech Syst Signal Process. 2019;125:4–20.
Ding H, Chen LQ. Designs, analysis, and applications of nonlinear energy sinks. Nonlinear Dyn. 2020;100:3061–107.
Georgiades F, Vakakis AF. Dynamics of a linear beam with an attached local nonlinear energy sink. Commun Nonlinear Sci Numer Simul. 2007;12:643–51.
Samani FS, Pellicano F. Vibration reduction on beams subjected to moving loads using linear and nonlinear dynamic absorbers. J Sound Vib. 2009;325:742–54.
Samani FS, Pellicano F. Vibration reduction of beams under successive traveling loads by means of linear and nonlinear dynamic absorbers. J Sound Vib. 2012;331:2272–90.
Ahmadabadi ZN, Khadem SE. Nonlinear vibration control of a cantilever beam by a nonlinear energy sink. Mech Mach Theory. 2012;50:134–49.
Ahmadabadi ZN, Khadem SE. Nonlinear vibration control and energy harvesting of a beam using a nonlinear energy sink and a piezoelectric device. J Sound Vib. 2014;333:4444–57.
Parseh M, Dardel M, Ghasemi MH. Investigating the robustness of nonlinear energy sink in steady state dynamics of linear beams with different boundary conditions. Commun Nonlinear Sci Numer Simul. 2015;29:50–71.
Kani M, Khadem SE, Pashaei MH, Dardel M. Vibration control of a nonlinear beam with a nonlinear energy sink. Nonlinear Dyn. 2015;83:1–22.
Kani M, Khadem SE, Pashaei MH, Dardel M. Design and performance analysis of a nonlinear energy sink attached to a beam with different support conditions. J Mech Eng Sci. 2015;230(4):527–42.
Bab S, Khadem SE, Mahdiabadi MK, Shahgholi M. Vibration mitigation of a rotating beam under external periodic force using a nonlinear energy sink (NES). J Vib Control. 2015;23(6):1001–25.
Parseh M, Dardel M, Ghasemi MH, Pashaei MH. Steady state dynamics of a non-linear beam coupled to a non-linear energy sink. Int J Non-Linear Mech. 2016;79:48–65.
Zhang YW, Hou S, Xu KF, Yang TZ, Chen LQ. Forced vibration control of an axially moving beam with an attached nonlinear energy sink. Acta Mech Solida Sin. 2017;30:674–82.
Chen JE, He W, Zhang W, Yao MH, Liu J, Sun M. Vibration suppression and higher branch responses of beam with parallel nonlinear energy sinks. Nonlinear Dyn. 2018;91:885–904.
Fang X, Wen JH, Yin JF, Yu DL. Highly efficient continuous bistable nonlinear energy sink composed of a cantilever beam with partial constrained layer damping. Nonlinear Dyn. 2017;87:2677–95.
Li HQ, Touze C, Pelat A, Gautier F. Combining nonlinear vibration absorbers and the Acoustic Black Hole for passive broadband flexural vibration mitigation. Int J Non-Linear Mech. 2021;129:103558.
Zhang Z, Ding H, Zhang YW, Chen LQ. Vibration suppression of an elastic beam with boundary inerter-enhanced nonlinear energy sinks. Acta Mech Solida Sin. 2021;37(3):387–401.
Acknowledgements
This work is supported by the National Natural Science Foundation of China (Grant No. 11972125) and the Fok Ying Tung Education Foundation (Grant No. 161049).
Author information
Authors and Affiliations
Contributions
All authors agree to publish the article “Dynamic Behavior and Vibration Suppression of a Generally Restrained Pre-pressure Beam Structure Attached with Multiple Nonlinear Energy Sinks”. According to the authors’ contributions to this work, the author’s rank is Yuhao Zhao, Jingtao Du, Yilin Chen, and Yang Liu. Jingtao Du is the corresponding author.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Appendices
Appendix A
Appendix B
Appendix C
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Zhao, Y., Du, J., Chen, Y. et al. Dynamic Behavior and Vibration Suppression of a Generally Restrained Pre-pressure Beam Structure Attached with Multiple Nonlinear Energy Sinks. Acta Mech. Solida Sin. 36, 116–131 (2023). https://doi.org/10.1007/s10338-022-00350-3
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10338-022-00350-3