Skip to main content
SpringerLink
Log in

Numerical and Experimental Investigations on Tunable Low-frequency Locally Resonant Metamaterials

  • Published:
Acta Mechanica Solida Sinica Aims and scope Submit manuscript

Abstract

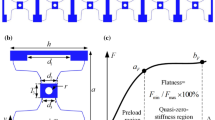
In this paper, a tunable locally resonant metamaterial is proposed for low-frequency band gaps. The local resonator composed of two pairs of folded slender beams and a proof mass is designed based on the theory of compliant mechanism. The design optimization on geometric parameters is carried out to fulfil the quasi-zero-stiffness property. The locally resonant metamaterial is formed by periodically arranged unit cells, and the transmittance of longitudinal wave is studied through three aspects: numerical predictions, finite element simulations and experimental tests. The variation trends revealed by these three methods match well with one another: the band gap moves to lower frequency and both its depth and width get smaller and smaller with the increase of pre-compression (\(\Delta \)). The band gap overlays the frequency range of 73.10–92.38 Hz and 16.78–19.49 Hz at \(\Delta = 0 \, \hbox {mm}\) and \(\Delta = 10 \, \hbox {mm}\), respectively, providing a wide range of tunability. Besides, the ultralow-frequency band gap can be achieved as \(\Delta \) approaches 10 mm. This study may provide an avenue for achieving the tunable ultralow-frequency locally resonant band gap.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  1. Chen JS, Sun CT. Wave propagation in sandwich structures with resonators and periodic cores. J Sandw Struct Mater. 2013;15:359–74.

    Article  Google Scholar 

  2. Wang T, Sheng M, Ding X, Yan X. Wave propagation and power flow in an acoustic metamaterial plate with lateral local resonance attachment. J Phys D Appl Phys. 2018;51:115306.

    Article  Google Scholar 

  3. Liu W, Yi B, Yoon GH, Choi H. Functionally graded phononic crystals with broadband gap for controlling shear wave propagation. Adv Eng Mater. 2020:2000645.

  4. Sun JH, Wu TT. Propagation of acoustic waves in phononic-crystal plates and waveguides using a finite-difference time-domain method. Phys Rev B. 2007;76:104304.

    Article  Google Scholar 

  5. Khelif A, Choujaa A, Benchabane S, Djafari-Rouhani B, Laude V. Guiding and bending of acoustic waves in highly confined phononic crystal waveguides. Appl Phys Lett. 2004;84:4400.

    Article  Google Scholar 

  6. Yu D, Wen J, Zhao H, Liu Y, Wen X. Vibration reduction by using the idea of phononic crystals in a pipe-conveying fluid. J Sound Vib. 2008;318:193–205.

    Article  Google Scholar 

  7. Nateghi A, Sangiuliano L, Claeys C, Deckers E, Pluymers B, Desmet W. Design and experimental validation of a metamaterial solution for improved noise and vibration behavior of pipes. J Sound Vib. 2019;455:96–117.

    Article  Google Scholar 

  8. Yu D, Wen J, Shen H, Xiao Y, Wen X. Propagation of flexural wave in periodic beam on elastic foundations. Phys Lett A. 2012;376:626–30.

    Article  Google Scholar 

  9. Zhu R, Huang GL, Hu GK. Effective dynamic properties and multi-resonant design of acoustic metamaterials. J Vib Acoust. 2012;134:031006.

    Article  Google Scholar 

  10. Cai C, Zhou J, Wu L, Wang K, Xu D, Ouyang H. Design and numerical validation of quasi-zero-stiffness metamaterials for very low-frequency band gaps. Compos Struct. 2020;236:111862.

    Article  Google Scholar 

  11. Qureshi A, Li B, Tan KT. Numerical investigation of band gaps in 3D printed cantilever-in-mass metamaterials. Sci Rep. 2016;6:28314.

    Article  Google Scholar 

  12. Balaji PS, Karthik SelvaKumar K. Applications of nonlinearity in passive vibration control: a review. J Vib Eng Technol. 2020.

  13. An X, Lai C, Fan H, Zhang C. 3D acoustic metamaterial-based mechanical metalattice structures for low-frequency and broadband vibration attenuation. Int J Solids Struct. 2020;191–192:293–306.

    Article  Google Scholar 

  14. Zhao H, Wen J, Yu D, Wen X. Low-frequency acoustic absorption of localized resonances: Experiment and theory. J Appl Phys. 2010;107:023519.

    Article  Google Scholar 

  15. Fan H, Yang L, Tian Y, Wang Z. Design of metastructures with quasi-zero dynamic stiffness for vibration isolation. Compos Struct. 2020;243:112244.

    Article  Google Scholar 

  16. Wang K, Zhou J, Wang Q, Ouyang H, Xu D. Low-frequency band gaps in a metamaterial rod by negative-stiffness mechanisms: Design and experimental validation. Appl Phys Lett. 2019;114:251902.

    Article  Google Scholar 

  17. Ren T, Liu C, Li F, Zhang C. Active tunability of band gaps for a novel elastic metamaterial plate. Acta Mech. 2020;231:4035–53.

    Article  MathSciNet  Google Scholar 

  18. Zhou W, Chen W, Chen Z, Lim CW. Actively controllable flexural wave band gaps in beam-type acoustic metamaterials with shunted piezoelectric patches. Eur J Mech A Solid. 2019;77:103807.

    Article  MathSciNet  Google Scholar 

  19. Zhu R, Huang GL, Huang HH, Sun CT. Experimental and numerical study of guided wave propagation in a thin metamaterial plate. Phys Lett A. 2011;375:2863–7.

    Article  Google Scholar 

  20. Zhu R, Liu XN, Hu GK, Sun CT, Huang GL. A chiral elastic metamaterial beam for broadband vibration suppression. J Sound Vib. 2014;333:2759–73.

    Article  Google Scholar 

  21. Wang T. Tunable band gaps in an inertant metamaterial plate with two-degree-of-freedom local resonance. Phys Lett A. 2020;384:126420.

    Article  MathSciNet  Google Scholar 

  22. Zhang Q, Zhang K, Hu G. Tunable fluid-solid metamaterials for manipulation of elastic wave propagation in broad frequency range. Appl Phys Lett. 2018;112:221906.

    Article  Google Scholar 

  23. Wang K, Zhou J, Xu D, Ouyang H. Tunable low-frequency torsional-wave band gaps in a meta-shaft. J Phys D Appl Phys. 2019;52:055104.

    Article  Google Scholar 

  24. Wang P, Casadei F, Shan S, Weaver JC, Bertoldi K. Harnessing buckling to design tunable locally resonant acoustic metamaterials. Phys Rev Lett. 2014;113:014301.

    Article  Google Scholar 

  25. Lan CC, Lee KM. Generalized shooting method for analyzing compliant mechanisms with curved members. J Mech Design. 2006;128:765–75.

    Article  Google Scholar 

  26. Lan CC, Wang JH, Chen YH. A compliant constant-force mechanism for adaptive robot end-effector operations. Proc IEEE Int Conf Robot Autom. 2010:2131–6.

  27. Lan CC, Cheng YJ. Distributed shape optimization of compliant mechanisms using intrinsic functions. J Mech Design. 2008;130:072304.

    Article  Google Scholar 

Download references

Acknowledgements

The authors gratefully acknowledge the support from the National Natural Science Foundation of China (11972152, 11832009), the National Key R&D Program of China (2017YFB1102801), and the Laboratory of Science and Technology on Integrated Logistics Support.

Author information

Authors and Affiliations

  1. State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body, Changsha, 410082, China

    Qida Lin, Jiaxi Zhou, Hongbin Pan, Daolin Xu & Guilin Wen

  2. College of Mechanical and Vehicle Engineering, Hunan University, Changsha, 410082, China

    Qida Lin, Jiaxi Zhou, Hongbin Pan, Daolin Xu & Guilin Wen

  3. School of Mechanical and Electric Engineering, Guangzhou University, Guangzhou, 510006, China

    Guilin Wen

Authors
  1. Qida Lin
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jiaxi Zhou
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Hongbin Pan
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Daolin Xu
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Guilin Wen
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jiaxi Zhou.

Ethics declarations

Declarations of Interest

The authors declare no conflict of interest.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Lin, Q., Zhou, J., Pan, H. et al. Numerical and Experimental Investigations on Tunable Low-frequency Locally Resonant Metamaterials. Acta Mech. Solida Sin. 34, 612–623 (2021). https://doi.org/10.1007/s10338-021-00220-4

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10338-021-00220-4

Keywords

Search

Navigation