Skip to main content
SpringerLink
Log in

Transient Response in a Bi-material Cylinder of Soft Ferromagnetic Material Subjected to Magnetic Shock

  • Published:
Acta Mechanica Solida Sinica Aims and scope Submit manuscript

Abstract

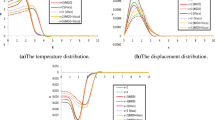
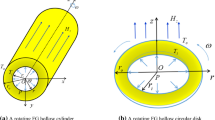
The transient response in a bi-material cylinder of soft ferromagnetic material under magnetic shock is investigated in this study. The analytical solutions for displacement and stress have been derived using the finite Hankel transform and the Laplace transform. The numerical examples show that the displacement and stress fields respond dynamically in the bi-material cylinder under magnetic shock. The derived displacement at the center and radial stress on the surface of the cylinder satisfy the boundary conditions, showing the correctness of calculation. The displacement and stress waves propagate from the surface to the center of the cylinder when the magnetic field is loaded. The stress fields increase from the center to the surface of the cylinder and are much larger than the quasi-static state since the waves reflect, collide and concentrate in the body of the cylinder. The method of this paper can be used in the design of soft ferromagnetic structures.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  1. Eringen AC, Maugin GA. Electrodynamics of continua. New York: Springer-Verlag; 1990.

    Book  Google Scholar 

  2. Brown Jr. Magnetoelastic interactions[M]. New York: Springer; 1966.

    Book  Google Scholar 

  3. Pao YH, Yeh CS. A linear theory for soft ferromagnetic elastic solids. Int J Eng Sci. 1973;11:415–36.

    Article  Google Scholar 

  4. Zhao R, Kima Y, Chester A, et al. Mechanics of hard-magnetic soft materials. J Mech Phys Solids. 2019;124:244–63.

    Article  MathSciNet  Google Scholar 

  5. Kurlyandskaya GV, Shcherbinin SV, Volchkov SO, et al. Soft magnetic materials for sensor applications in the high frequency range. J Magn Magn Mater. 2018;459:154–8.

    Article  Google Scholar 

  6. Azuma D, Ito N, Ohta M. Recent progress in Fe-based amorphous and nanocrystalline soft magnetic materials. J Magn Magn Mater. 2020;501: 166373.

    Article  Google Scholar 

  7. Parton VZ. Fracture mechanics of piezoelectric materials. Acta Astronaut. 1976;3:671–83.

    Article  Google Scholar 

  8. Shindo Y. The linear magnetoelastic problem of two coplanar Griffith cracks in a soft ferromagnetic elastic strip. J Appl Mech. 1982;49:69–74.

    Article  Google Scholar 

  9. Podilchuk NY, Tereshchenko LN. A magnetoelastic field in a ferromagnetic with an elliptic inclusion. Int Appl Mech. 2002;38:585–93.

    Article  Google Scholar 

  10. Liang W, Fang DN, Shen YP. Mode I crack in a soft ferromagnetic material. Fatigue Fract Eng Mater Struct. 2001;25:519–26.

    Article  Google Scholar 

  11. Lin CB, Yeh CS. The magnetoelastic problem of a crack in a soft ferromagnetic solid. Int J Solids Struct. 2002;39:1–17.

    Article  Google Scholar 

  12. Bagdasarian GY, Hasanian DJ. Magnetoelastic interaction between a soft ferromagnetic elastic half-plane with a crack and a constant magnetic field. Int J Solids Struct. 2000;37:5371–83.

    Article  Google Scholar 

  13. Gao CF, Mai YW, Wang BL. Effects of magnetic fields on cracks in a soft ferromagnetic material. Eng Fract Mech. 2008;75:4863–75.

    Article  Google Scholar 

  14. Hasebe N, Omatsu N. Analysis of a kinked crack in soft ferromagnetic and paramagnetic elastic materials subjected to uniform magnetic field intensity. Eng Fract Mech. 2017;184:141–53.

    Article  Google Scholar 

  15. Mcivor IK. The elastic cylindrical shell under radial impulse. J Appl Mech. 1966;33:831–7.

    Article  Google Scholar 

  16. Wu XD, Zheng JY, Chen YJ, et al. Dynamic response of a discrete multi-layered cylinder due to thermal shock(In Chinese). Eng Mech. 2008;25:109–15.

    Google Scholar 

  17. Wang X. An elastodynamics solution for anisotropic axially symmetric problems (In chinese). Acta Mech Sin. 1997;29:606–11.

    Google Scholar 

  18. Dai HL, Xiao X, Fu YM. Analytical solutions of stresses in functionally graded piezoelectric hollow structures. Solid State Commun. 2010;150:763–7.

    Article  Google Scholar 

  19. Wang X. Dynamic thermal shock in a layered cylinder with initial interface pressure(In chinese). Appl Math Mech. 1999;20:1065–71.

    Google Scholar 

  20. Jiang Q, Gao CF, Xu XL. Research on the electro-elastic response in an electrostrictive cylinder subjected to an electrical shock (In chinese). Chin Q Mech. 2015;36:602–10.

    Google Scholar 

  21. Chen WQ, Ding HJ. A state-space-based stress analysis of a multilayered spherical shell with spherical isotropy. J Appl Mech. 2001;68:101–14.

    Article  Google Scholar 

  22. Yin XC. Multiple impacts of two concentric hollow cylinders with zero clearance. Int J Solids Struct. 1997;34:4597–616.

    Article  Google Scholar 

  23. Chand D, Sharma JN, Sud SP. Transient generalized magnetothermo-elastic waves in a rotating half-space. Int J Eng Sci. 1990;28:547–56.

    Article  Google Scholar 

  24. Dai HL, Fu YM, Liu TX. Electromagnetoelastic dynamic response of transversely isotropic piezoelectric hollow spheres in a uniform magnetic field. J Appl Mech. 2007;74:65–73.

    Article  Google Scholar 

  25. Dai HL, Fu YM. Magnetothermoelastic stress in orthotropic hollow cylinders due to radially symmetric thermal and mechanical loads. Struct Eng Mech. 2006;24:699–707.

    Article  Google Scholar 

  26. Dai HL, Wang X. Magneto-thermo-electro-elastic transient response in a piezoelectric hollow cylinder subjected to complex loadings. Int J Solids Struct. 2006;43:5628–46.

    Article  Google Scholar 

  27. Wang X, Dai HL. Magnetothermodynamic stress and perturbation of magnetic field vector in a hollow cylinder. J Therm Stresses. 2004;3:269–88.

    Article  Google Scholar 

  28. Dai HL, Wang X. Magnetoelastodynamic stress and perturbation of magnetic field vector in an orthotropic laminated hollow cylinder. Int J Eng Sci. 2006;44:365–78.

    Article  Google Scholar 

  29. Yan B, Ma HY, Zhang L, et al. Electromagnetic shunt damping for shock isolation of nonlinear vibration isolators. J Sound Vib. 2020;479:115370.

  30. Biswas D, Ray C. Comparative study on transient response analysis of hybrid laminated composite plates with experimental verification. J Sound Vib. 2019;453:43–64.

    Article  Google Scholar 

  31. Chao Chang, Gao CF, Shi Y. Two-dimensional problems in a soft ferromagnetic solid with an elliptic hole or a crack. Int J Eng Sci. 2012;52:1–21.

  32. Cinelli G. An extension of the finite Hankel transform and application. Int J Eng Sci. 1965;3:534–50.

    Article  MathSciNet  Google Scholar 

  33. Jiang Q, Gao CF. On the general expressions of finite Hankel transform. Sci China Phys Mech Astron. 2010;53:2125–30.

    Article  Google Scholar 

Download references

Acknowledgements

This work was supported by the National Natural Science Foundation of China under Grant No. 11802145 and Jiangsu Provincial Natural Science Foundation of China under Grant No. BK20191450.

Author information

Authors and Affiliations

  1. College of Civil Engineering, Tongji University, Shanghai, 200092, China

    Zhangjianing Cheng

  2. School of Transportation and Civil Engineering, Nantong University, Nantong, 226019, China

    Quan Jiang

Authors
  1. Zhangjianing Cheng
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Quan Jiang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Quan Jiang.

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Cheng, Z., Jiang, Q. Transient Response in a Bi-material Cylinder of Soft Ferromagnetic Material Subjected to Magnetic Shock. Acta Mech. Solida Sin. 34, 286–296 (2021). https://doi.org/10.1007/s10338-020-00202-y

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10338-020-00202-y

Keywords

Search

Navigation