Skip to main content
SpringerLink
Log in

Plane Analysis for an Inclusion in 1D Hexagonal Quasicrystal Using the Hypersingular Integral Equation Method

  • Published:
Acta Mechanica Solida Sinica Aims and scope Submit manuscript

Abstract

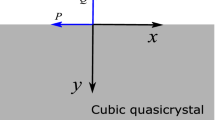
A model of a thin elastic inclusion embedded in an infinite 1D hexagonal quasicrystal is discussed. The atomic arrangements of the matrix and the inclusion are both periodic along the \(x_{1}\)-direction and quasiperiodic along the \(x_{2}\)-direction in the \(ox_{1}x_{2}\)-coordinate system. Using the hypersingular integral equation method, the inclusion problem is reduced to solving a set of hypersingular integral equations. Based on the exact analytical solution of the singular phonon and phason stresses near the inclusion front, a numerical method of the hypersingular integral equation is proposed using the finite-part integral method. Finally, the numerical solutions for the phonon and phason stress intensity factors of some examples are given.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  1. Shechtman D, Blech I, Gratias D, et al. Metallic phase with long-range orientational order and no translational symmetry. Phys Rev Lett. 1984;53:1951–3.

    Article  Google Scholar 

  2. Levine D, Joseph SP. Quasicrystals: a new class of ordered structures. Phys Rev Lett. 1984;53:2477–80.

    Article  Google Scholar 

  3. Yang W, Ding DH, Wang RH, et al. Thermodynamics of equilibrium properties of quasicrystals. Z Phys B Condens Matter. 1997;100:447–54.

    Article  Google Scholar 

  4. Biggs BD, Li Y, Poon SJ. Electronic properties of icosahedral, approximant, and amorphous phases of an Al–Cu–Fe alloy. Phys Rev B. 1991;43:8747–50.

    Article  Google Scholar 

  5. Pierce FS, Guo Q, Poon SJ. Enhanced insulatorlike electron transport behavior of thermally tuned quasicrystalline states of Al–Pd–Re alloys. Phys Rev Lett. 1994;73:2220.

    Article  Google Scholar 

  6. Bak P. Phenomenological theory of icosahedral incommensurate (quasiperiodic) order in Mn–Al alloys. Phys Rev Lett. 1985;54:1517.

    Article  Google Scholar 

  7. Levine D, Lubensky TC, Ostlund S, et al. Elasticity and dislocations in pentagonal and icosahedral quasicrystals. Phys Rev Lett. 1985;54:1520.

    Article  Google Scholar 

  8. Peng Y, Fan T. Elastic theory of 1D-quasiperiodic stacking of 2D crystals. J Phys Condens Matter. 2000;12:9381–7.

    Article  Google Scholar 

  9. De P, Pelcovits RA. Disclinations in pentagonal quasicrystals. Phys Rev B. 1987;36:9304–7.

    Article  Google Scholar 

  10. Ding DH, Wang RH, Yang WG, et al. General expressions for the elastic displacement fields induced by dislocations in quasicrystals. J Phys Condens Matter. 1995;7:5423.

    Article  Google Scholar 

  11. Fan TY, Guo LH. The final governing equation and fundamental solution of plane elasticity of icosahedral quasicrystals. Phys Lett A. 2005;341:235–9.

    Article  MATH  Google Scholar 

  12. Li LH, Fan TY. Final governing equation of plane elasticity of icosahedral quasicrystals and general solution based on stress potential function. Chin Phys Lett. 2006;23:2519–21.

    Article  Google Scholar 

  13. Eshelby JD. The determination of the elastic field of an ellipsoidal inclusion, and related problems. Proc R Soc Lond. 1957;241:376–96.

    Article  MathSciNet  MATH  Google Scholar 

  14. Muskhelishvili NI. Some basic problems of the mathematical theory of elasticity. Math Gaz. 1953;48:351.

    Google Scholar 

  15. Wang ZY, Zhang HT, Chou YT. Characteristics of the elastic field of a rigid line inhomogeneity. J Appl Mech. 1985;52:729–829.

    Google Scholar 

  16. Atkinson C. Some ribbon-like inclusion problems. Int J Eng Sci. 1973;11:243–66.

    Article  MATH  Google Scholar 

  17. Qin TY, Tang RJ. Finite-part integral and boundary element method to solve inclusion problems. Acta Mater Compos Sin. 1996;13:65–70.

    Google Scholar 

  18. Tao FM, Zhang MH, Tang RJ. The interaction problem between the elastic line inclusions. Appl Math Mech. 2002;23:371–9.

    Article  MathSciNet  MATH  Google Scholar 

  19. Chen TY. The rotation of a rigid ellipsoidal inclusion embedded in an anisotropic piezoelectric medium. Int J Solids Struct. 1993;30:1983–95.

    Article  MATH  Google Scholar 

  20. Deng W, Meguid SA. Analysis of conducting rigid inclusion at the interface of two dissimilar piezoelectric materials. J Appl Mech. 1998;65:76–84.

    Article  Google Scholar 

  21. Pan E. Eshelby problem of polygonal inclusions in anisotropic piezoelectric full- and half-planes. J Mech Phys Solids. 2004;52:567–89.

    Article  MathSciNet  MATH  Google Scholar 

  22. Ru CQ. Eshelby inclusion of arbitrary shape in an anisotropic plane or half-plane. Acta Mech. 2003;160:219–34.

    Article  MATH  Google Scholar 

  23. Li G, Wang BL, Han JC. Exact solution for elliptical inclusion in magnetoelectroelastic materials. Int J Solids Struct. 2010;47:419–26.

    Article  MATH  Google Scholar 

  24. Wang YZ. Interfacial line inclusion between two dissimilar thermo-electro-magneto-elastic solids. Acta Mech. 2015;226:2861–72.

    Article  MathSciNet  MATH  Google Scholar 

  25. Guo XP, Chen JF, Yu HL, et al. A study on the microstructure and tribological behavior of cold-sprayed metal matrix composites reinforced by particulate quasicrystal. Surf Coat Technol. 2015;268:94–8.

    Article  Google Scholar 

  26. Sakly A, Kenzari S, Bonina D, et al. A novel quasicrystal-resin composite for stereolithography. Mater Design (1980–2015). 2014;56:280–5.

    Article  Google Scholar 

  27. Wang X. Eshelby’s problem of an inclusion of arbitrary shape in a decagonal quasicrystalline plane or half-plane. Int J Eng Sci. 2004;42:1911–30.

    Article  MathSciNet  MATH  Google Scholar 

  28. Shi W. Collinear periodic cracks and/or rigid line inclusions ofantiplane sliding mode in one-dimensional hexagonal quasicrystal. Appl Math Comput. 2009;215:1062–7.

    MathSciNet  MATH  Google Scholar 

  29. Wang X, Schiavone P. Decagonal quasicrystalline elliptical inclusions under thermomechanical loading. Acta Mech Solida Sin. 2014;27:518–30.

    Article  Google Scholar 

  30. Guo JH, Zhang ZY, Xing YM. Antiplane analysis for an elliptical inclusion in 1D hexagonal piezoelectric quasicrystal composites. Philos Mag. 2016;96:349–69.

    Article  Google Scholar 

  31. Guo JH, Yu J, Si RL. A semi-inverse method of a Griffith crack in one-dimensional hexagonal quasicrystals. Appl Math Comput. 2013;219:7445–9.

    MathSciNet  MATH  Google Scholar 

  32. Guo JH, Pan E. Three-phase cylinder model of one-dimensional hexagonal piezoelectric quasi-crystal composites. J Appl Mech Trans ASME. 2016;83:081007.

    Article  Google Scholar 

  33. Wang Y, Guo JH. Effective electroelastic constants for three-phase confocal elliptical cylinder model in piezoelectric quasicrystal composites. Appl Math Mech Engl Ed. 2018;39:797–812.

    Article  MathSciNet  MATH  Google Scholar 

  34. Ioakimidis NI. Application of finite-part integrals to the singular integral equations of crack problems in plane and three-dimensional elasticity. Acta Mech. 1982;45:31–47.

    Article  MathSciNet  MATH  Google Scholar 

  35. Kaya AC, Erdogan F. On the solution of integral equations with strongly singular kernels. Q Appl Math. 1987;45:105–22.

    Article  MathSciNet  MATH  Google Scholar 

  36. Ding DH, Yang W, Hu C, et al. Generalized elasticity theory of quasicrystals. Phys Rev B Condens Matter. 1993;48:7003–10.

    Article  Google Scholar 

  37. Ding HJ, Wang GQ, Chen WQ. Fundamental solutions for plane problem of piezoelectric materials. Sci China Ser E Technol Sci. 1997;40:331–6.

    Article  MATH  Google Scholar 

  38. Erdogan F. Mixed boundary value problems in mechanics of materials. Multiscale Funct Graded Mater. 2008;973:772–83.

    Google Scholar 

  39. Fan CY, Yuan YP, Pan YB, et al. Analysis of cracks in one-dimensional hexagonal quasicrystals with the heat effect. Int J Solids Struct. 2017;120:146–56.

    Article  Google Scholar 

  40. Lee JS, Jiang LZ. Exact electroelastic analysts of piezoelectric laminae via state space approach. Int J Solids Struct. 1996;33:977–90.

    Article  MATH  Google Scholar 

  41. Li XY, Li PD, Kang GZ. Crack tip plasticity of a thermally loaded penny-shaped crack in an infinite space of 1D QC. Acta Mech Solida Sin. 2015;28:471–83.

    Article  Google Scholar 

  42. Zhang LL, Wu D, Xu WS, et al. Green’s functions of one-dimensional quasicrystal bi-material with piezoelectric effect. Phys Lett A. 2016;380:3222–8.

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

The authors would like to express their special thanks to the National Natural Science Foundation of China (Project No. 11172320 and No. 11272341).

Author information

Authors and Affiliations

  1. College of Science, China Agricultural University, Beijing, 100083, China

    Fei Lou, Taiyan Qin & Chunhui Xu

  2. College of Engineering, China Agricultural University, Beijing, 100083, China

    Ting Cao

Authors
  1. Fei Lou
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ting Cao
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Taiyan Qin
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Chunhui Xu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Taiyan Qin.

Appendix A: Material-Related Constants

Appendix A: Material-Related Constants

$$\begin{aligned} A_i= & {} s_1^2 s_2^2 s_3^2 (C_{44} K_2 -R_3^2 -C_{33} K_2 s_i^2 -C_{44} K_1 s_i^2 +2R_3 R_2 s_i^2 +C_{33} K_1 s_i^4 -R_2^2 s_i^4 )/s_i \\ B_i= & {} s_1^2 s_2^2 s_3^2 (-C_{13} K_2 -C_{44} K_2 +R_3^2 +R_3 R_1 +C_{13} K_1 s_i^2 +C_{44} K_1 s_i^2 -R_3 R_2 s_i^2 -R_1 R_2 s_i^2 )\\ C_i= & {} s_1^2 s_2^2 s_3^2 (C_{13} R_3 -C_{44} R_1 +C_{33} R_3 s_i^2 +C_{33} R_1 s_i^2 -C_{13} R_2 s_i^2 -C_{44} R_2 s_i^2 ) \\ D_i= & {} s_1^2 s_2^2 s_3^2 (C_{11} K_2 -C_{44} K_2 s_i^2 -C_{11} K_1 s_i^2 +R_3^2 s_i^2 +2R_3 R_1 s_i^2 +R_1^2 s_i^4 +C_{44} K_1 s_i^4)/s_i \\ E_i= & {} s_1^2 s_2^2 s_3^2 (-C_{11} R_3 -C_{13} R_3 s_i^2 -C_{13} R_1 s_i^2 -C_{44} R_1 s_i^2 +C_{11} R_2 s_i^2 -C_{44} R_2 s_i^4 )/s_i \\ G_i= & {} s_1^2 s_2^2 s_3^2 (C_{11} C_{44} +C_{13}^2 s_i^2 -C_{11} C_{13} s_i^2 +2C_{13} C_{44} s_i^2 +C_{33} C_{44} s_i^4 )/s_i \\ b_1= & {} 2\pi C_{11} (C_{44} K_2 -R_3^2 )(s_1^2 -s_2^2 )(s_3^2 -s_1^2 ) \\ b_2= & {} 2\pi C_{11} (C_{44} K_2 -R_3^2 )(s_2^2 -s_1^2 )(s_3^2 -s_2^2 ) \\ b_3= & {} 2\pi C_{11} (C_{44} K_2 -R_3^2 )(s_1^2 -s_3^2 )(s_3^2 -s_2^2 ) \\ a= & {} C_{33} C_{44} K_1 -C_{44} R_2^2 ,\ d=C_{11} C_{44} K_2 -C_{11} R_3^2 \\ b= & {} C_{33} \left[ {(R_1 +R_3 )^{2}-C_{44} K_2 )} \right] -K_1 \left[ {C_{11} C_{33} +C_{44}^2 -(C_{13} +C_{44} )^{2}} \right] \\&+R_2 \left[ {2R_3 C_{44}+R_2 C_{11}-2(C_{13}+C_{44})(R_1 +R_3)}\right] \\ c= & {} C_{11} (2R_2 R_3 -C_{33} K_2 -C_{44} K_1 )-C_{13} (2R_1 R_2 +2R_3^2 -C_{13} K_2 -2C_{44} K_2 )+C_{44} R_1^2 \\ \gamma _{11}= & {} C_{11} \frac{A_i }{b_i }+C_{13} \frac{B_i s_i }{b_i }+R_1 \frac{C_i s_i }{b_i },\quad \gamma _{12} =C_{11} \frac{B_i s_i }{b_i }+C_{13} \frac{D_i s_i^2 }{b_i }+R_1 \frac{E_i s_i^2 }{b_i }\\ \gamma _{21}= & {} C_{13} \frac{A_i }{b_i }-C_{33} \frac{B_i s_i }{b_i }-R_2 \frac{C_i s_i }{b_i },\quad \gamma _{22} =C_{13} \frac{B_i s_i }{b_i }+C_{33} \frac{D_i s_i^2 }{b_i }+R_2 \frac{E_i s_i^2 }{b_i }\\ \gamma _{31}= & {} C_{44} \frac{A_i s_i^2 }{b_i }+C_{44} \frac{B_i s_i }{b_i }+R_3 \frac{C_i s_i }{b_i },\quad \gamma _{32} =-C_{44} \frac{B_i s_i }{b_i }+C_{44} \frac{D_i }{b_i }+R_3 \frac{E_i }{b_i } \\ \gamma _{41}= & {} R_1 \frac{A_i }{b_i }-R_2 \frac{B_i s_i }{b_i }-K_1 \frac{C_i s_i }{b_i },\quad \gamma _{42} =R_1 \frac{B_i s_i }{b_i }+R_2 \frac{D_i s_i^2 }{b_i }+K_1 \frac{E_i s_i^2 }{b_i } \\ \gamma _{51}= & {} R_3 \frac{A_i s_i^2 }{b_i }+R_3 \frac{B_i s_i }{b_i }+K_2 \frac{C_i s_i }{b_i },\quad \gamma _{52} =-R_3 \frac{B_i s_i }{b_i }+R_3 \frac{D_i }{b_i }+K_2 \frac{E_i }{b_i} \end{aligned}$$

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Lou, F., Cao, T., Qin, T. et al. Plane Analysis for an Inclusion in 1D Hexagonal Quasicrystal Using the Hypersingular Integral Equation Method. Acta Mech. Solida Sin. 32, 249–260 (2019). https://doi.org/10.1007/s10338-018-0072-0

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10338-018-0072-0

Keywords

Search

Navigation