Skip to main content
SpringerLink
Log in

Extension/Compression-Controlled Complete Band Gaps in 2D Chiral Square-Lattice-Like Structures

  • Original Paper
  • Published:
Acta Mechanica Solida Sinica Aims and scope Submit manuscript

A Correction to this article was published on 22 November 2018

This article has been updated

Abstract

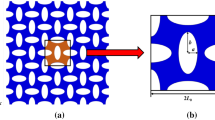
Achieving tunable band gaps in a structure by external stimuli is of great importance in acoustic applications. This paper aims to investigate the tunability of band gaps in square-lattice-like elastic periodic structures that are usually not featured with notable band gaps. Endowed with chirality, the periodic structures here are able to undergo imperfection-insensitive large deformation under extension or compression. The influences of geometric parameters on band gaps are discussed via the nonlinear finite element method. It is shown that the band gaps in such structures with curved beams can be very rich and, more importantly, can be efficiently and robustly tuned by applying appropriate mechanical loadings without inducing buckling. As expected, geometry plays a more significant role than material nonlinearity does in the evolution of band gaps. The dynamic tunability of band gaps through mechanical loading is further studied. Results show that closing, opening, and shifting of band gaps can be realized by exerting real-time global extension or compression on the structure. The proposed periodic structure with well-designed chiral symmetry can be useful in the design of particular acoustic devices.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

Change history

  • 22 November 2018

    In all the articles in Acta Mechanica Solida Sinica, Volume 31, Issues 1–4, the copyright is incorrectly displayed as “The Chinese Society of Theoretical and Applied Mechanics and Technology ” where it should be “The Chinese Society of Theoretical and Applied Mechanics”.

References

  1. Kushwaha MS, Halevi P, Dobrzynski L, Djafarirouhani B. Acoustic band structure of periodic elastic composites. Phys Rev Lett. 1993;71(13):2022–5.

    Article  Google Scholar 

  2. Maldovan M. Sound and heat revolutions in phononics. Nature. 2013;503(7475):209.

    Article  Google Scholar 

  3. Cummer SA, Christensen J, Alù A. Controlling sound with acoustic metamaterials. Nat Rev Mater. 2016;1:16001.

    Article  Google Scholar 

  4. Casadei F, Beck BS, Cunefare KA, Ruzzene M. Vibration control of plates through hybrid configurations of periodic piezoelectric shunts. J Intell Mater Syst Struct. 2012;23(10):1169–77.

    Article  Google Scholar 

  5. Vasseur JO, Hladky-Hennion AC, Djafari-Rouhani B, Duval F, Dubus B, Pennec Y, Deymier PA. Waveguiding in two-dimensional piezoelectric phononic crystal plates. J Appl Phys. 2007;101(11):114904.

    Article  Google Scholar 

  6. Casadei F, Dozio L, Ruzzene M, Cunefare KA. Periodic shunted arrays for the control of noise radiation in an enclosure. J Sound Vib. 2010;329(18):3632–46.

    Article  Google Scholar 

  7. Kushwaha MS, Djafaric-Rouhani B. Complete acoustic stop bands for cubic arrays of spherical liquid balloons. J Appl Phys. 1996;80(6):3191–5.

    Article  Google Scholar 

  8. Kafesaki M, Sigalas MM, Economou EN. Elastic wave band gaps in 3-D periodic polymer matrix composites. Solid State Commun. 1995;96(5):285–9.

    Article  Google Scholar 

  9. Vasseur JO, Djafari-Rouhani B, Dobrzynski L, Kushwaha MS, Halevi P. Complete acoustic band gaps in periodic fibre reinforced composite materials: the carbon/epoxy composite and some metallic systems. J Phys Condens Matter. 1994;6(42):8759.

    Article  Google Scholar 

  10. Vasseur JO, Djafari-Rouhani B, Dobrzynski L, Deymier PA. Acoustic band gaps in fibre composite materials of boron nitride structure. J Phys Condens Matter. 1997;9(35):7327.

    Article  Google Scholar 

  11. Khelif A, Deymier PA, Djafari-Rouhani B, Vasseur JO, Dobrzynski L. Two-dimensional phononic crystal with tunable narrow pass band: application to a waveguide with selective frequency. J Appl Phys. 2003;94(3):1308–11.

    Article  Google Scholar 

  12. Zhou XZ, Wang YS, Zhang C. Effects of material parameters on elastic band gaps of two-dimensional solid phononic crystals. J Appl Phys. 2009;106(1):014903.

    Article  Google Scholar 

  13. Su XX, Wang YF, Wang YS. Effects of Poisson’s ratio on the band gaps and defect states in two-dimensional vacuum/solid porous phononic crystals. Ultrasonics. 2012;52(2):255–65.

    Article  Google Scholar 

  14. Gei M, Roccabianca S, Bacca M. Controlling bandgap in electroactive polymer-based structures. IEEE/ASME Trans Mechatron. 2011;16(1):102–7.

    Article  Google Scholar 

  15. Getz R, Kochmann DM, Shmuel G. Voltage-controlled complete stopbands in two-dimensional soft dielectrics. Int J Solids Struct. 2017;113:24–36.

    Article  Google Scholar 

  16. Bertoldi K, Boyce MC. Mechanically triggered transformations of phononic band gaps in periodic elastomeric structures. Phys Rev B. 2008;77(5):052105.

    Article  Google Scholar 

  17. Bertoldi K, Boyce MC. Wave propagation and instabilities in monolithic and periodically structured elastomeric materials undergoing large deformations. Physical Review B. 2008;78(18):184107.

    Article  Google Scholar 

  18. Rudykh S, Boyce MC. Transforming wave propagation in layered media via instability-induced interfacial wrinkling. Phys Rev Lett. 2014;112(3):034301.

    Article  Google Scholar 

  19. Huang Y, Shen XD, Zhang CL, Chen WQ. Mechanically tunable band gaps in compressible soft phononic laminated composites with finite deformation. Phys Lett A. 2014;378(30):2285–9.

    Article  Google Scholar 

  20. Shan S, Kang SH, Wang P, Qu C, Shian S, Chen ER, Bertoldi K. Harnessing multiple folding mechanisms in soft periodic structures for tunable control of elastic waves. Adv Funct Mater. 2014;24(31):4935–42.

    Article  Google Scholar 

  21. Huang YL, Gao N, Bao RH, Chen WQ. A novel algorithm for post-buckling analysis of periodic structures and its application. Chin J Comput Mech. 2016;33(4):509–15 (in Chinese).

    Google Scholar 

  22. Wang P, Shim J, Bertoldi K. Effects of geometric and material nonlinearities on tunable band gaps and low-frequency directionality of phononic crystals. Phys Rev B. 2013;88(1):014304.

    Article  Google Scholar 

  23. Dong HW, Wang YS, Wang YF, Zhang C. Reducing symmetry in topology optimization of two-dimensional porous phononic crystals. AIP Adv. 2015;5(11):117149.

    Article  Google Scholar 

  24. Chen Y, Li T, Scarpa F, Wang L. Lattice metamaterials with mechanically tunable Poisson’s ratio for vibration control. Phys Rev Appl. 2017;7(2):024012.

    Article  Google Scholar 

  25. Casadei F, Rimoli JJ. Anisotropy-induced broadband stress wave steering in periodic lattices. Int J Solids Struct. 2013;50(9):1402–14.

    Article  Google Scholar 

  26. Trainiti G, Rimoli JJ, Ruzzene M. Wave propagation in undulated structural lattices. Int J Solids Struct. 2016;97:431–44.

    Article  Google Scholar 

  27. Abaqus Analysis User’s Guide, Abaqus 6.14. Vélizy-Villacoublay: Dassault Systèmes Simulia Corp. 2014.

  28. Holzapfel GA. Nonlinear solid mechanics. Chichester: Wiley; 2000.

    MATH  Google Scholar 

  29. Ogden RW. Non-linear elastic deformations. New York: Courier Corporation; 1997.

    Google Scholar 

  30. Achenbach JD. Wave propagation in elastic solids. Amsterdam: North Holland; 1973.

    MATH  Google Scholar 

  31. Kittel C. Introduction to solid state physics. Chichester: Wiley; 2005.

    MATH  Google Scholar 

Download references

Acknowledgements

The work was supported by the National Natural Science Foundation of China (Nos. 11532001, 11621062, and 11272281) and open project of State Key Laboratory of Explosion Science and Technology (Beijing Institute of Technology) under Grant No. KFJJ16-04M. Partial support from the Fundamental Research Funds for the Central Universities (No. 2016XZZX001-05) is also acknowledged.

Author information

Authors and Affiliations

  1. Department of Engineering Mechanics, Zhejiang University, Hangzhou, 310027, China

    Y. L. Huang, N. Gao, W. Q. Chen & R. H. Bao

  2. State Key Lab of CAD & CG, Zhejiang University, Hangzhou, 310058, China

    W. Q. Chen

  3. Key Laboratory of Soft Machines and Smart Devices of Zhejiang Province, Zhejiang University, Hangzhou, 310027, China

    W. Q. Chen & R. H. Bao

  4. Soft Matter Research Center, Zhejiang University, Hangzhou, 310027, China

    W. Q. Chen

Authors
  1. Y. L. Huang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. N. Gao
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. W. Q. Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. R. H. Bao
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to R. H. Bao.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Huang, Y.L., Gao, N., Chen, W.Q. et al. Extension/Compression-Controlled Complete Band Gaps in 2D Chiral Square-Lattice-Like Structures. Acta Mech. Solida Sin. 31, 51–65 (2018). https://doi.org/10.1007/s10338-018-0004-z

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10338-018-0004-z

Keywords

Search

Navigation