Abstract
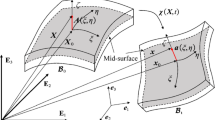
The objectives of this study are to employ the meshless local Petrov-Galerkin method (MLPGM) to solve three-dimensional shell problems. The computational accuracy of MLPGM for shell problems is affected by many factors, including the dimension of compact support domain, the dimension of quadrture domain, the number of integral cells and the number of Gauss points. These factors’ sensitivity analysis is to adopt the Taguchi experimental design technology and point out the dimension of the quadrature domain with the largest influence on the computational accuracy of the present MLPGM for shells and give out the optimum combination of these factors. A few examples are given to verify the reliability and good convergence of MLPGM for shell problems compared to the theoretical or the finite element results.
Similar content being viewed by others
References
Krysl, P. and Belytschko, T., Analysis of thin shells by the element-free Galerkin method. International Journal of Solids and Structures, 1996, 33: 3057–3080.
Noguchi, H., Kawashima, T. and Miyamura, T., Element free analysis of shell and spatial structures. International Journal for Numerical Methods in Engineering, 2000, 47: 1215–1240.
Atluri, S.N. and Zhu, T., A new meshless local Petrov-Galerkin (MLPG) approach in computational mechanics. Computational Mechanics, 1998, 22(1): 117–127.
Atluri, S.N., Cho, J.Y. and Kim, H.G., Analysis of thin beams, using the meshless local Petrov-Galerkin method, with generalized moving least squares interpolation. Computational Mechanics, 1999, 24(4): 334–347.
Xiong, Y.B. and Long, S.Y., Local Petrov-Galerkin method for a thin plate. Applied Mathematics and Mechanics, 2004, 25(2): 189–196 (in Chinese).
Xiong, Y.B., Long, S.Y., Hu, D.A. and Li, G.Y., A meshless local Petrov-Galerkin method for geometrically nonlinear problems. Acta Mechanica Solida Sinica, 2005, 18(4): 348–356.
Phadke, M.S., Quality Engineering using Robust Design. Prentice-Hall International Editions, 1989.
Timoshenko, S., Theory of Plates and Shells. McGraw-HillBook Company, Inc, 1959.
Simo, J.C., Fox, D.D. and Rifai, M.S., On a stress resultant geometrically exact shell model—Part II, The linear theory; Computational aspects. Computer Methods in Applied Mechanics and Engineering, 1989, 73: 53–92.
Liu, G.R., Meshfree Methods Moving beyond the Finite Element method. CRC Press, 2003.
Hinton, E. and Owen, D.R.J., Finite Element Software for Plate and Shells. Swansea: Pineridge Press, 1984.
Author information
Authors and Affiliations
Additional information
Project supported by the Scientific Foundation of National Outstanding Youth of China (No. 50225520) and the Science Foundation of Shandong University of Technology of China (No. 2006KJM33).
Rights and permissions
About this article
Cite this article
Li, D., Lin, Z. & Li, S. Numerical Analysis of Mindlin Shell by Meshless Local Petrov-Galerkin Method. Acta Mech. Solida Sin. 21, 160–169 (2008). https://doi.org/10.1007/s10338-008-0819-0
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10338-008-0819-0