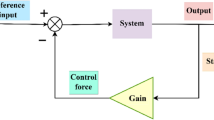
Abstract
A feedback control optimization method of partially observable linear structures via stationary response is proposed and analyzed with linear building structures equipped with control devices and sensors. First, the partially observable control problem of the structure under horizontal ground acceleration excitation is converted into a completely observable control problem. Then the Itô stochastic differential equations of the system are derived based on the stochastic averaging method for quasi-integrable Hamiltonian systems and the stationary solution to the Fokker-Plank-Kolmogorov (FPK) equation associated with the Itô equations is obtained. The performance index in terms of the mean system energy and mean square control force is established and the optimal control force is obtained by minimizing the performance index. Finally, the numerical results for a three-story building structure model under El Centro, Hachinohe, Northridge and Kobe earthquake excitations are given to illustrate the application and the effectiveness of the proposed method.
Similar content being viewed by others
References
Fleming, W.H. and Soner, H.M., Controlled Markov Processes and Viscosity Solutions. New York: Springer, 1993.
Yong, J.M. and Zhou, X.Y., Stochastic Control, Hamiltonian Systems and HJB Equations. New York: Springer, 1999.
Zhu, W.Q. and Ying, Z.G., Optimal nonlinear feedback control of quasi Hamiltonian systems. Science in China, Series A, 1999, 42: 1213–1219.
Zhu, W.Q., Ying, Z.G. and Soong, T.T., An optimal nonlinear feedback control strategy for randomly excited structural systems. Nonlinear Dynamics, 2001, 24: 31–51.
Zhu, W.Q. and Yang, Y.Q., Stochastic averaging of quasi non-integrable Hamiltonian systems. ASME Journal of Applied Mechanics, 1997, 64: 157–164.
Zhu, W.Q., Huang, Z.L. and Yang, Y.Q., Stochastic averaging of quasi integrable Hamiltonian systems. ASME Journal of Applied Mechanics, 1997, 64: 975–984.
Zhu, W.Q., Huang, Z.L. and Suzuki, Y., Stochastic averaging and Lyapunov exponent of quasi partially integrable Hamiltonian systems. International Journal of Non-linear Mechanics, 2002, 37: 419–437.
Zhu, W.Q. and Ying, Z.G., Nonlinear stochastic optimal control of partially observable linear structures. Engineering Structures, 2002, 24: 333–342.
Zhu, W.Q. and Ying, Z.G., Stochastic optimal control of partially observable nonlinear quasi Hamiltonian systems. Journal of Zhejiang University Science, 2004, 5: 1313–1317.
Zhu, W.Q., Nonlinear Stochastic Dynamics and Control—Hamiltonian Framework. Beijing: Science Press, 2003 (in Chinese).
Ou, J.P., Structure Vibration Control—Active, Semi-active and Intelligent Control. Beijing: Science Press, 2003 (in Chinese).
Fleming, W.H. and Rishel R.W., Deterministic and Stochastic Optimal Control. Berlin: Spring-Verlag, 1975.
Bensoussan, A., Stochastic Control of Partially Observable Systems. Cambridge: Cambridge University Press, 1992.
Antoniou, A., Digital Filters: Analysis, Design and Application. New York: McGraw-Hill, Inc., 1993: 444–446.
Author information
Authors and Affiliations
Additional information
Project supported by the National Natural Science Foundation of China under a key grant (No.10332030), the Research Fund for the Doctoral Program of Higher Education of China (No. 20060335125) and the Zhejiang Provincial Natural Science Foundation of China (No. Y607087).
Rights and permissions
About this article
Cite this article
Li, X., Ying, Z. Feedback control optimization for seismically excited buildings. Acta Mech. Solida Sin. 20, 342–349 (2007). https://doi.org/10.1007/s10338-007-0740-y
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10338-007-0740-y