Abstract
Height–diameter modeling is most often performed using non-linear regression models based on ordinary differential equations. In this study, new models of tree height dynamics involving a stochastic differential equation and mixed-effects parameters are examined. We use a stochastic differential equation to describe the dynamics of the height of an individual tree. The first model is defined by a Gompertz shape stochastic differential equation. The second Gompertz shape stochastic differential equation model with a threshold parameter can be considered an extension of the three-parameter stochastic Gompertz process through the addition of a fourth parameter. The parameters are estimated through discrete sampling of diameter and height and through the maximum likelihood procedure. We use data from tropical Atlantic moist forest trees to validate our modeling technique. The results indicate that our models are able to capture tree height behavior quite accurately. All the results are implemented in the MAPLE symbolic algebra system.

Similar content being viewed by others

References
Calama R, Montero G (2004) Interregional nonlinear height–diameter model with random coefficients for stone pine in Spain. Can J For Res 34:150–163. doi:10.1139/03-199
Garcia O (1983) A stochastic differential equation model for the height growth of forest stands. Biometrics 39:1059–1072
Gompertz B (1825) On the nature of the function expressive of the law of human mortality, and on a new mode of determining the value of life contingencies. Philos Trans R Soc Lond B 115:513–585
Gutierrez R, Gutierrez-Sanchez R, Nafidi A, Ramos E (2006) A new stochastic Gompertz diffusion process with threshold parameter: computational aspects and applications. Appl Math Comput 183:738–747
Hosoda K, Iehara T (2010) Biomass equations for four shrub species in subtropical China. J For Res 15(5):299–306
Itô K (1942) On stochastic processes. Jpn J Math 18:261–301
Kenzo T, Furutani R, Hattori D, Kendawang JJ, Tanaka S, Sakurai K, Ninomiya I (2009) Allometric equations for accurate estimation of above-ground biomass in logged-over tropical rainforests in Sarawak, Malaysia. J For Res 14:365–372
Liang WM, Fei LX (2000) Research on nonlinear height–diameter models. J For Res 13(1):75–79
Lumbres RIC, Cabral DE, Parao MR, Seo YO, Lee YJ (2012) Evaluation of height–diameter models for three tropical plantation species in the Philippines. Asia Life Sci 21:455–468
McCulloch CE, Neuhaus JM (2012) Prediction of random effects in linear and generalized linear models under model misspecification. Biometrics 67:270–279
Monagan MB, Geddes KO, Heal KM, Labahn G, Vorkoetter SM, McCarron J, DeMarco P (2007) Maple Advanced programming Guide. Maplesoft, Canada
Picchini U, Ditlevsen S, De Gaetano A (2011) Practical estimation of high dimensional stochastic differential mixed-effects models. Comput Stat Data Anal 55:1426–1444
Rupšys P, Petrauskas E (2010a) The bivariate Gompertz diffusion model for tree diameter and height distribution. For Sci 56:271–280
Rupšys P, Petrauskas E (2010b) Quantifying tree diameter distributions with one-dimensional diffusion processes. J Biol Syst 18:205–221
Rupšys P, Petrauskas E (2012) Analysis of height curves by stochastic differential equations. Int J Biomath 5(5):1250045. doi:10.1142/S1793524511001878
Rupšys P, Petrauskas E, Mažeika J, Deltuvas R (2007) The Gompertz type stochastic growth law and a tree diameter distribution. Balt For 13:197–206
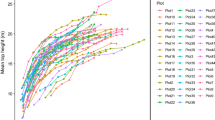
Scaranello MA, Alves LF, Vieira SA, Camargo PB, Joly CA, Martinelli LA (2012) height–diameter relationships of tropical Atlantic moist forest trees in southeastern Brazil. Sci Agr 69:26–37
Staudhammer CL, LeMay VM (2001) Introduction and evaluation of possible indices of stand structural diversity. Can J For Res 31:1105–1115
Suzuki T (1971) Forest transition as a stochastic process. Mitt. Forstl. Bundesversuchsanstalt Wien 91:69–86
Tanaka K (1986) A stochastic model of diameter growth in an even-aged pure forest stand. J Jpn For Soc 68:226–236
Tanaka K (1988) A stochastic model of height growth in an even aged pure forest stand: why is the coefficient of variation of the height distribution smaller than that of the diameter distribution? J Jpn For Soc 70:20–29
Temesgen H, Gadow KV (2004) Generalized height–diameter models––an application for major tree species in complex stands of interior British Columbia. Eur J For Res 123:45–51
Uhlenbeck G, Ornstein LS (1930) On the theory of Brownian motion. Phys Rev 36:823–841
Vanclay JK (1995) Growth models for tropical forests: a synthesis of models and methods. For Sci 41:4–42
VanderSchaaf CL (2012) Mixed-effects height–diameter models for commercially and ecologically important conifers in Minnesota. North J App For 29:15–20
Zeng HQ, Liu QJ, Feng ZW, Ma ZQ (2010) Aboveground biomass equations for individual trees of Cryptomeria japonica, Chamaecyparis obtusa and Larix kaempferi in Japan. J For Res 15:83–90
Acknowledgments
The author appreciates the anonymous reviewers and the editor for their helpful comments on the manuscript.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
In the context of this study, there is only one height measurement for each tree. First, the maximum log-likelihood function is derived for fixed-effects models (in this case, the parameter of random effects, \( \phi_{i} \), is assumed to be equal to its mean value E(\( \phi_{i} \)) = 0, i = 1,…,M). Second, the maximum log-likelihood function is derived for mixed-effects models.
The fixed-effects parameters α, β, γ, and σ are estimated through the maximum likelihood procedure using discrete sampling and conditional probability density functions (Eqs. 6 and 12). Let us consider a discrete sample of the process (\( h_{1}^{i} ,\,h_{2}^{i} ,\, \ldots ,\,h_{{n_{i} }}^{i} \)) at the diameters (\( d_{1}^{i} ,\,d_{2}^{i} ,\, \ldots ,d_{{n_{i} }}^{i} \)), where n i is the number of observed trees of the ith stand, i = 1,2,…,M. Under the initial condition P(H(0) = 1.37) = 1, the associated log-likelihood function can be obtained by the following expression:
where the density function f(h, d) takes the forms of Eq. 6 or 12 and θ = α, β, σ or θ = α, β, σ, γ, respectively, with the random-effects parameters \( \phi_{i} \) ≡ 0, i = 1, 2, …, M.
The maximum log-likelihood function for mixed-effects models defined by Eqs. 5 and 11 takes the following form:
where θ = α, β, γ, σ is the vector of the fixed-effects parameters (the same for all stands) and \( \phi_{i} \) is the random-effects parameter (stand-specific), which is assumed to follow a univariate normal distribution, p(\( \phi_{i} \)|\( \sigma_{\phi } \)), with a mean of 0 and constant variance \( \sigma_{\phi }^{2} \). Unfortunately, the integral in Eq. 29 does not have a closed-form solution. Because the analytic expression for the integrand in Eq. 29 is known, the Laplace method may be used (Picchini et al. 2011). The log-likelihood function for the mixed-effects models defined by Eqs. 5 and 11 is approximately given by:
where
The maximization of \( {\text{LL}}_{{_{\text{m}} }} \left( {\theta , \sigma_{\phi } } \right) \) is a nested optimization problem. The internal optimization step estimates the \( \left( {{\hat \phi }_{i} } \right) \) for every stand i = 1,2,…,M. The external optimization step maximizes \( {\text{LL}}_{{_{\text{m}} }} \left( {\theta , \sigma_{\phi } } \right) \) after substituting the value of \( \left( {{ \hat \phi }_{i} } \right) \) into Eq. 30.
About this article
Cite this article
Rupšys, P. Height–diameter models with stochastic differential equations and mixed-effects parameters. J For Res 20, 9–17 (2015). https://doi.org/10.1007/s10310-014-0454-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10310-014-0454-1