Introduction

The experimental multi-GNSS orbit combination service was initiated in 2019 by the International GNSS Service (IGS, Johnston et al. 2017) Analysis Centre Coordinator (ACC). The current combination software, used for many years for the IGS GPS and GLONASS combinations (Beutler et al. 1995; Kouba and Mireault, 1998; Weber and Springer 2001), has been employed for the generation of multi-GNSS orbits. The combined orbit products are not yet considered to be the final IGS products at this time, but instead, they can be used for the comparison of individual analysis centers contributing to IGS and the multi-GNSS Pilot Project (MGEX, Montenbruck et al. 2017). The combined products include a plethora of different satellite systems and generations; GPS: Block IIA, IIR, IIR-M, IIF, III; GLONASS: M, M+ , K1; Galileo: In-Orbit-Validation (IOV), Full Operational Capability (FOC), and FOC in eccentric orbits; BeiDou-2: Geostationary (GEO), Inclined Geosynchronous (IGSO), and Medium Earth Orbiters (MEOs); BeiDou-3 and BeiDou-3S: IGSO and MEO, manufactured by China Academy of Space Technology (CAST) and Shanghai Engineering Center for Microsatellites (SECM, Zhao et al. 2018); QZSS: GEO and eccentric IGSO.

All new GNSS satellites, except for GPS, are equipped with laser retroreflector arrays (LRA) for Satellite Laser Ranging (SLR). The International Laser Ranging Service (ILRS, Pearlman et al. 2019a, b) initiated in 2015 a series of intensive GNSS tracking campaigns, which resulted in a substantial increase in collected SLR observations to GNSS (Bury et al. 2019a), which was possible thanks to the optimized and enhanced tracking strategy at ILRS stations. SLR observations to GNSS can be used for the orbit modeling validation (Springer et al. 1999; Arnold et al. 2015; Kazmierski et al. 2018), precise orbit determination of GNSS satellites (Bury et al. 2019c), co-location of GNSS and SLR techniques in space (Thaller et al. 2011; Bruni et al. 2018), and deriving global geodetic parameters (Sośnica et al. 2018a, 2019).

The goal of this study is to assess the quality of the IGS experimental multi-GNSS combined orbits based on SLR observations and on the mean position errors from the orbit combinations. SLR provides independent orbit validation results even for those satellites, which are considered only by one analysis center, and the standard deviation values (STDs) of the combination are not provided. We also analyze STD values provided in the combined SP3 orbit files, which reflect the consistency level between orbits from different analysis centers.

Methodology

The experimental multi-GNSS products are made available on a weekly basis, with a delay of about 20 days, which is similar to the final IGS combination delay (Griffiths and Ray 2009; Johnston et al. 2017; Griffiths 2019). The combination includes final and rapid MGEX submissions, as well as final IGS submissions, all combined together because the purpose of the experimental combination is to include as many submissions as possible. Only the MGEX submission is employed in the case of analysis centers providing both the final IGS and MGEX submissions, whereas IGS products are used then only for comparison purposes. The same weighted average approach developed by Beutler et al. (1995) is used for generating combined orbits. Orbits are combined as weighted averages computed over all centers. Each center and satellite are given a position weight computed from the center’s absolute deviation to the unweighted average orbit. Correlations between components of the position vector and positions referring to different epochs, that is, the time correlations, are neglected. Under these simplifications, the combination procedure for each coordinate reads as follows:

First, a simple mean of the orbit solutions by different analysis centers is calculated:

$$ \hat{x}_{0}^{X,Y,Z} \left( t \right) = \frac{1}{n}\mathop \sum \limits_{k = 1}^{n} x_{k}^{X,Y,Z} \left( t \right) $$

where \( x_{k}\) is the orbit solution of the kth analysis center for each \(X, Y, Z\) orbital component at the epoch \(t\), and \(n\) is the total number of analysis centers providing orbit solution for a satellite.

For each orbit solution, seven-parameter Helmert transformation between the individual orbit and the mean orbit is estimated by minimizing the mean absolute deviation (MAD) of the position components of the two orbits as a robust function. This L1-norm minimization is performed using a bracketing and bisection algorithm for finding the root of the derivative of the robust function, as described by Press et al. (2007). Each orbit solution is transformed using the above estimated Helmert parameters, and the weights for the analysis centers are calculated based on the deviations of each orbit and its transformed version:

$$ w_{k} = \left( {\frac{1}{{{\text{MAD}}\left( {d^{3D}_{k} } \right)}}} \right)^{2} $$

where \(d^{3D}_{k} \left( t \right) = \left| {x_{k}^{T} \left( t \right) - x_{k} \left( t \right)} \right|\), and MAD is the mean absolute deviation of the position components of the orbit solution \(x_{k}\) from the positions of the transformed orbit \(x_{k}^{T}\) for a particular day. By using these weights for the analysis center data, the weighted mean of the orbits is calculated:

$$ \hat{x}_{1}^{X,Y,Z} \left( t \right) = \frac{1}{{\mathop \sum \nolimits_{k = 1}^{n} w_{k} }}\mathop \sum \limits_{k = 1}^{n} w_{k} x_{k}^{X,Y,Z} \left( t \right) $$

Another set of the seven-parameter Helmert transformation is estimated between each orbit solution and the above weighted mean using the same L1-norm minimization as described for the previous step. Each orbit is then transformed using the estimated transformation parameters. Finally, the combined orbit is calculated as the weighted mean of the transformed orbit positions \(x_{k}^{T}\), with the weights as calculated before:

$$ \hat{x}_{F}^{X,Y,Z} \left( t \right) = \frac{1}{{\mathop \sum \nolimits_{k = 1}^{n} w_{k} }}\mathop \sum \limits_{k = 1}^{n} w_{k} x_{k}^{{T^{{^{X,Y,Z} }} }} \left( t \right) $$

In the case of very large RMS values for a satellite in the combined orbit exceeding triple STD, that satellite is removed from the orbit solution, and in case of a very large RMS for an orbit solution, or very large transformation parameters estimated for an orbit solution, that orbit solution is completely removed from the combination. In such cases, the above algorithm is repeated until none of the above issues persist in the combination.

Position components \(x_{k} \) represent the individual orbit solutions in the earth-fixed frame. Individual orbit components (X, Y, Z) could be considered independently. However, in this approach, the weights are calculated based on differences of full position 3D vectors. According to Beutler et al. (1995), the weighted mean of the orbits satisfies the equation of motion provided that the weights are constant.

The weighted average software was originally developed by Timon Springer and Gerhard Beutler in 1993 and used by IGS for the combination of GPS and later for GLONASS orbits (Beutler et al. 1995; Weber and Springer 2001; Kouba 2009). The IGS ACC initiated a web service providing weighted RMS (WRMS) of the individual orbit solutions with respect to the combined orbits and estimated transformation parameters between individual solutions and the IGS combined orbits. The service also generates plots showing the time series of transformation parameters, see: https://acc.igs.org/mgex_experimental.html. The mean WRMS of individual contributors in the combination is 10, 25, 14, 52, and 46 mm for GPS, GLONASS, Galileo, BeiDou, and QZSS, respectively. Transformations to the IGS reference frame are not yet applied due to the variety of the products used for the combinations. Not all analysis centers provide earth rotation parameters and products in SINEX files (Mansur et al. 2020). The errors resulting from this neglect are much smaller than the errors in the orbit determination process. For most of the centers, the rotation errors do not exceed 0.1 mas, which corresponds to 3 mm on the earth surface and 12 mm at GNSS heights. The weighting scheme used in this experimental combination is the same as the one used in the current operational combination. An improved weighting that considers the differences between different orbit types is being developed in an upgraded combination software, which aims at a fully operational multi-GNSS combination. So far, only GNSS orbits are combined, which satisfies the needs of users processing double-differenced GNSS observations, whereas a proper GNSS clock combination is still pending for undifferenced solutions. In this research, the analysis period spans from April 29 to September 29, 2019.

GPS

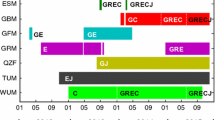
Combined GPS orbits are generated on the basis of twelve analysis centers, six of which emerge from the MGEX solutions with the suffix -M, and another six from IGS final, see Table 1. Two IGS solutions from CODE and GFZ and the combined IGS rapid (IGR) and final (IGS) solutions are included for statistical reasons in the combination reports but not included in the combination solutions due to their redundancy. The current agreement between experimental IGS combination and IGR or IGS products is at the level of 3 and 4 mm, respectively, whereas most of the individual centers have an RMS of about 10 mm when compared to the combined orbits. So far, only two GPS satellites from Block IIA, SVN 35 and 36, have been equipped with LRA for SLR. These satellites were deactivated in 2013 and 2014 and recently are occasionally being reactivated again providing very sparse SLR data, which is why the SLR analysis for GPS is omitted here. However, it is planned that future GPS III satellites, launched after 2026, will carry LRAs for SLR tracking.

Table 1 Contribution of individual analysis centers and their products to the combined orbits of different GNSS systems
Full size table

GLONASS

The combined GLONASS solutions are based on six MGEX centers, two IGS centers (denoted with a suffix ‘-X’), and two GLONASS-only contributors: IAC, and the SLR-only solution provided by MCC. The MCC contribution and IGS GLONASS final products (IGL) are not considered for the combination, but only for comparison purposes. The GLONASS constellation is mainly composed of GLONASS-M satellites broadcasting navigation signal on two frequencies L1 and L2, three M+ and two GLONASS-K1 with the additional L3 signal (Montenbruck et al. 2015, 2017). GLONASS-M and M+ are equipped with rectangular LRAs with 112 corner cubes, whereas K1s are equipped with a ring retroreflector surrounding the microwave transmitter antennas consisting of 123 corner cubes. Despite a large area of the ring retroreflector, the precision of the SLR measurements should be better for single-photon detectors because the probability of the reflection from each corner cube is the same. Therefore, when an SLR station collects hundreds or thousands of single full-rate reflections and generates one normal point based on 300 s of observations, the mean SLR observation corresponds to the centroid of the LRA onboard the GLONASS-K1 (Sośnica et al. 2015; Rodríguez et al. 2019). The future GLONASS-K2 will be equipped with ring LRAs with the number of corner cubes reduced to 36. GLONASS-K R26 (SVN 801) was the first, purely experimental satellite of the new type that was launched in 2011. This satellite cannot be tracked by all stations and is not considered by all analysis centers. The official status of SVN 801 is ‘flight test.’ GLONASS-K R09 (SVN 802), launched in 2014, is a newer K1-type satellite that is fully operational and transmits a signal on a channel that is accessible to all receivers.

Two GLONASS-M R02 (SVN 747) and R15 (SVN 857), one M + R05 (SVN 856), and K1 R09 (SVN 802) are intensively being tracked by the ILRS stations with the highest priority since July 2019, whereas the tracking of the remaining constellation depends on the capabilities and time availability of SLR stations. Before that, the ILRS recommended tracking of R02, R09, R11, and R14 (SVNs 747, 802, 853, and 732) and with a lower priority also R03, R18, R21, and R17 (SVNs 744, 854, 855, and 851).

Galileo

The Galileo constellation consists of three active IOV satellites, one IOV transmitting signal only on one frequency and thus not included in the combination, 19 active FOC satellites, and two FOC satellites launched into eccentric orbits that are used for geodesy and general relativity studies (Steigenberger and Montenbruck 2017; Hadas et al. 2019; Delva et al. 2015). Galileo IOV: E12 (SVN 102), and FOC: E01 (SVN 210), E08 (SVN 208), as well as FOC eccentric: E14 (SVN 202), were selected by the ILRS for intensive tracking. Before July 2019, the ILRS recommended tracking E12, E14, E09, E01, E36, E13, E15, and E04 (SVNs 102, 202, 209, 210, 219, 220, 221, and 213) with decreasing priorities. Galileo IOV satellites are equipped with rectangular retroreflectors with 84 corner cubes of a diameter of 33 mm, whereas FOCs are equipped with 60 corner cubes with an optical diameter of just 28.2 mm. Therefore, SLR tracking of FOC satellites is much more challenging than the tracking of IOV for SLR stations. However, the signature effect and the RMS of SLR normal points for FOC are reduced, especially for those SLR stations that use multi-photon detectors (Sośnica et al. 2018b).

BeiDou

In October 2019, the BeiDou constellation consisted of 34 active satellites and nine satellites not included in the operational mode (4 experimental BeiDou-3S and 5 BeiDou-3). BeiDou-2 includes five GEO, seven IGSO, and three MEO satellites, whereas BeiDou-3 comprises 18 MEO and one IGSO active spacecraft manufactured by SECM and CAST (Lv et al. 2020). The characteristics of the Chinese constellation can be followed at the MGEX Web site (https://mgex.igs.org/IGS_MGEX_Status_BDS.php). BeiDou-2 IGSO and MEO combined orbit solutions are based on five centers (see Table 1). The BeiDou-2 GEO orbits are based on GFM and WUM, because other centers do not consider GEO satellites or, as in the case of TUM, provide incomplete coverage of BeiDou-2 GEO satellites with the differences of mean orbits exceeding several meters. BeiDou-3 MEO orbits are generated only by WUM. The ILRS selected for intensive tracking four BeiDou-3: 3-M2 (C20, SVN 202), 3-M3 (C21, SVN 203), 3-M9 (C29, SVN 207), and 3-M10 (C30, SVN 208). Before July 2019, also BeiDou-2: C08, C10, C11, C13 (SVNs 008, 010, 012, 017), were scheduled for SLR tracking. BeiDou-2 MEO and BeiDou-3 SECM are equipped with LRA consisting of 42 corner cubes, whereas GEO and IGSO with 90 corner cubes, all of which have corner cube diameters of 33 mm. Two BeiDou-3 CAST from the ILRS priority list are equipped with retroreflectors consisting of 38 corner cubes.

QZSS

QZSS combined orbits are based on five MGEX centers; however, COM does not include solutions for the QZSS GEO satellite (J07, SVN 003), whereas JAM provides solutions only for the very first QZS-1 IGSO spacecraft (J01, SVN 001). All QZSS satellites are equipped with LRAs of 56-corner cubes of 41 mm in diameter and are scheduled in the ILRS priority list for tracking.

Internal evaluation of combined orbits

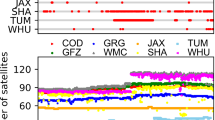
Figure 1 shows the number of GNSS satellites included in the combined IGS products. GPS, Galileo, and GLONASS are on a stable level of 32, 24, and 23 active spacecrafts. The number of BeiDou satellites in the combined products varies between 10 and 33 because BeiDou-3 data are currently being processed only by one center, which is subject to outages in case of product delays or processing errors. The number of considered QZSS satellites varies between 1 and 4.

Fig. 1
figure 1

Number of satellites from different systems included in the experimental IGS combined orbit products for the period from April 29 to September 29, 2019

Full size image

The combined orbits in SP3 format include not only the precise positions and clocks of the satellites but also information on the quality of the combination, i.e., STD of weighted position residuals from the combination, for those satellite orbits which are generated by more than one analysis center. However, the STD from SP3 files should be interpreted as a function of the consistency between orbits from different centers rather than the absolute orbit accuracy. Most of the analysis centers employ similar orbit models, e.g., the Empirical CODE Orbit Model (ECOM, Beutler et al. 1994), or an extended version with twice-per-revolution parameters included, the so-called ECOM2 (Arnold et al. 2015). Some of the centers employ, in addition, a priori box-wing models (Springer et al. 2019). Therefore, the consistency level of the orbit solutions employing the same models may be at a high level, whereas all solutions may be affected by the same systematic errors. The systematic errors in orbit positions can thus better be assessed using independent observational techniques, such as SLR.

Figure 2 shows the orbital STD values from the SP3 files for 3D positions and the radial component, which has a fundamental meaning for positioning due to the extensive impact on the signal-in-space range error (SISRE, Montenbruck et al. 2018). The STD values in radial \(m_{r}\) are calculated using the variance–covariance propagation law as:

$$ m_{r} = \sqrt {{\varvec{e}}_{r} \cdot C_{S} \cdot {\varvec{e}}_{r}^{T} } $$
Fig. 2
figure 2

Precision (consistency) of combined IGS satellite orbits based on SP3 files

Full size image

where the radial direction is calculated as \({\varvec{e}}_{r} = \frac{{{\varvec{r}}_{{\varvec{s}}} }}{{r_{s} }}\), with \({\varvec{r}}_{{\varvec{s}}}\) being the satellite position vector from SP3, and \(C_{S}\) is the diagonal variance matrix containing the squares of STD of the X, Y, and Z position components from SP3.

The radial precision for GPS satellites is at the level of 5 mm for all satellites, except for G04 with STD of 11 mm. G04 was occupied by the new GPS III (SVN74) satellite between January and July 2019 and again after October 2019. Apparently, the orbit models and antenna offsets used at different IGS analysis centers might be inconsistent or improper for the new GPS III satellite.

The radial precision for Galileo satellites is 8 mm, with no prominent difference between IOV, FOC, and FOC in eccentric orbits. For GLONASS, the radial precision is 9 mm for all satellites and 11 mm for R01 (SVN 730), R19 (SVN 720), and the experimental GLONASS-K1 R26 (801). The smallest radial STD of 7.6 mm is for R09 (SVN 802)—the second experimental GLONASS-K1 satellite.

For BeiDou-2, two groups can be distinguished: GEO with the mean radial STD of 21 mm, and IGSO and MEO with mean STD of 14 mm. The radial STD of QZSS IGSO is equal to 15 mm and thus corresponds well to other IGSO satellites. The 3D mean STD values are 37, 24, 15, 9, 26, and 16 mm for BeiDou GEO, BeiDou IGSO&MEO, Galileo, GPS, QZSS, and GLONASS, respectively.

Validation of IGS experimental combined multi-GNSS orbits using SLR

The GLONASS system is supported by the Russian network of SLR stations established in Asia, Europe, Africa, and South America, which results in a substantial number of SLR observations to selected GLONASS satellites (Fig. 3). The Galileo constellation is equally tracked by the European SLR stations, whereas other SLR stations track the Galileo satellites included in the ILRS priority list. GEO satellites are very challenging targets for laser ranging and have limited visibilities from SLR stations. Thus, the number of SLR observations to C01 and J07 is very low. One BeiDou-2 MEO (C11), three IGSO (C08, C10, and C13), and four BeiDou-3 MEO (CAST C20, C21; SECM C29, C30) were tracked by SLR in the period considered in this research.

Fig. 3
figure 3

Number of SLR observations (normal points) to different GNSS satellites

Full size image

The precision of the SLR measurements to GNSS strongly depends on the laser pulse width, timer and detector type used at the ILRS station, the number of collected photons, LRA size and corner cube arrangement, and data screening procedures used to generate SLR normal points. For satellites observed in zenith, the precision is 4–8 mm and decreases to 20–30 mm for satellites at low elevation angles due to signature effect of flat LRAs (https://ilrs.cddis.eosdis.nasa.gov/missions/satellite_missions/current_missions/ga02_stadata.html). The overall precision of SLR normal points to GNSS is between 10 and 20 mm for most of the stations and 4 mm for Matera due to a different screening procedure employed.

The SLR residuals are differences between SLR measurements and the theoretical distances to satellites based on IGS orbit positions. The SLR measurements are corrected by tropospheric delay models (Mendes and Pavlis 2004), effects emerging from general relativity, satellite eccentricities, and LRA offset corrections provided by mission operators. The processing strategy is the same as typically employed at the ILRS Associated Analysis Center at UPWr. (Zajdel et al. 2017; Otsubo et al. 2019) using the modified version of Bernese GNSS Software (Dach et al. 2015). The Bernese GNSS Software v.5.2 has the full capability of processing GPS and GLONASS observations, whereas Galileo processing is possible with some limitations. The modified version allows for processing Galileo, BeiDou, and QZSS data with a large number of GNSS satellites as used in the service www.govus.pl. The ILRS version of the International Terrestrial Reference Frame, SLRF2014, the ILRS eccentricity and data handling files, and SLR observations have been obtained from the ILRS Data Centers (Noll et al. 2019).

Figure 4 shows the results of the SLR validation for individual satellites. The smallest STD of residuals is 20, 24, and 24 mm for Galileo FOC eccentric, IOV, and FOC, respectively. For GLONASS, the STD of SLR residuals is 29, 27, 22, and 31 mm for GLONASS-M, M + , K1 R09, and the experimental K1 R26. For BeiDou-2, the STD is 87, 51, and 29 mm for GEO, IGSO, and MEO satellites, whereas for BeiDou-3, STD is 41 and 37 mm for CAST and SECM, respectively. QZSS has the STD of 59, 74, and 81 mm for QZS-1, other QZSS IGSO, and GEO, respectively.

Fig. 4
figure 4

SLR residual analysis for IGS experimental orbits. GLONASS-K1 is indicated by ‘*,’ whereas GLONASS-M+ and R15 are indicated with ‘ + ’

Full size image

The mean SLR offset is below 2 mm for Galileo FOC, FOC eccentric, and GLONASS-K1 R09. These satellites are equipped with either small-size LRAs or LRAs with the ring-shape corner cube arrangement so that they minimize the SLR signature effect, which is a systematic effect emerging from the laser reflection from multiple corner cubes. The large positive offsets of SLR residuals of 26 and 29 mm is visible for M + R05, R12, R21, and M R15, (SVNs 856, 858, 855, and 857) despite the very low STD of SLR residuals for the latter satellite (Fig. 4). This can be associated with the wrong value of LRA or antenna offset for the M+ satellites. GLONASS-M R15 (SVN 857) was launched recently in November 2018 and shows a similar SLR offset of + 31 mm to that of all other M+ satellites, despite it still officially belongs to the previous M-generation (Steigenberger et al. 2019). We assume that the construction of the R15 must be similar to M+ , and hence, in the statistics, R15 is considered together with the M+ satellites. One Galileo satellite, E22 (SVN 204), was affected by the failure of both hydrogen masers. Thus, the satellite was deactivated in February 2018. However, E22 was activated for a 2-week test period in June 2019, which resulted in a large negative offset of SLR residuals of − 40 mm.

BeiDou-3 satellites have small mean offsets between − 8 and 0 mm, the offset of BeiDou-2 MEO is − 9 mm, GLONASS-M satellites have a mean offset of − 10 mm, and the values for Galileo IOV are − 11 mm. The remaining satellites have larger offsets, which should be associated with the inferior quality of the orbit determination for GEO and IGSO.

From the comparison between SLR residuals from Fig. 4 and the mean radial precision from Fig. 2, one may conclude that for MEO satellites, the mean orbit STD values in the radial direction are three times lower than those from SLR residuals. In the case of GEO and IGSO, the orbit errors are four times lower than SLR residuals. The SLR residuals provide an independent validation tool for GNSS orbits, especially for the radial component. However, they are affected as well by SLR-specific systematic errors, such as systematic range and time biases, the blue-sky effect, and the satellite signature effect (Arnold et al. 2019). The SLR signature effect is a dependency between the real reflection point and the real distance to a satellite LRA centroid due to different laser incidence angles at the laser retroreflector array. For SLR stations operating in the multi-photon regime, the strongest registered reflection is always associated with the nearest edge of the flat retroreflector array when inclined with respect to the SLR station. The registered distance is shorter as the mean reflection point does not reach the optical centroid of the retroreflector array. For single-photon SLR stations operating with low-energy laser pulses, the probability of the reflection from each corner cube is the same, and after collecting several thousands of reflections, the mean observation corresponds to the optical centroid of the SLR retroreflector (Sośnica et al. 2015, 2018b). The blue-sky effect is related to the weather dependency of SLR observations. SLR observations are typically collected under blue skies when the atmospheric pressure deforms the earth crust downwards because of the atmospheric pressure loading and generates a systematic effect that is detectable in SLR products (Sośnica et al. 2013; Bury et al. 2019b).

The SLR residuals typically overestimate the total error of the radial orbit component due to SLR-specific systematic errors and LRA signature effect, whereas the radial consistency factor from SP3 files underestimates the total orbit error due to some systematic errors that are common in all IGS orbit solutions. The latter errors include the solar radiation pressure modeling errors, satellite attitude modeling errors, satellite and receiver antenna offsets and variations for individual frequencies, as well as errors in signal propagation models, such as tropospheric delay and higher-order ionospheric delay modeling errors.

Figure 5 shows the SLR residuals plotted as a function of the sun elevation angle above the orbital plane (absolute value of β) and the satellite argument of latitude with respect to the latitude of the sun (Δu). Galileo IOV and FOC show a pattern with SLR residuals shifted toward negative values for Δu close to 180°. This pattern was very large for the reduced ECOM and could substantially be reduced when introducing the extended ECOM2 or even almost eliminated when using the a priori box-wing model based on Galileo metadata with ECOM (Bury et al. 2019a). The pattern is due to the cuboid shape of Galileo satellites with the ratio between the X- and Z-bus area of 1.3:3.0, where the latter carries the transmitter antennas. Galileo IOVs show large negative residuals of about − 50 mm for maximum |β| angles when the sun is almost perpendicular to the orbital plane. The highest maximum |β| angles of 76° occur currently only for the Galileo C-plane (Sośnica et al. 2018b). Fortunately, no prominent issues with the orbit determination of eclipsing satellites, when |β|< 12.3°, are visible for Galileo, despite the asymmetrically distributed radiators on the satellite bus.

Fig. 5
figure 5

SLR residuals in millimeters as a function of the sun elevation angle above the orbital plane (absolute value of β) and the satellite argument of latitude with respect to the latitude of the sun (Δu)

Full size image

GLONASS-M and M+ are characterized by positive SLR residuals for Δu close to 180°, which is opposite to the situation of Galileo satellites. This can be explained by the fact that GLONASS-M and M+ are cylindrical with a small surface of the Z-bus side compared to the surface of the cylinder side. Neglecting the estimation of twice-per-revolution accelerations in the satellite–sun direction typically results in systematic effects similar to those observed for M and M+ (Arnold et al. 2015). SLR residuals to GLONASS-K1 are similar to those satellites that have well-performing orbit models due to K1′s regular cuboid shape (Fig. 5). SLR residuals to GLONASS-M+ are systematically shifted toward positive residuals almost for all β angles.

BeiDou-2 IGSO shows very prominent systematic errors. These range from − 160 mm when Δu is close to 0° to + 100 mm for Δu close to 180° (Fig. 4). The pattern is similar to that of GLONASS-M satellites, which could be explained by a much smaller area of the Z-bus surface when compared to the X-bus surface and mismodeling of the higher-order solar radiation pressure perturbing terms. The pattern for BeiDou-2 MEO is similar to that of GLONASS-M satellites, whereas BeiDou GEO and QZSS satellites show large-scale SLR residuals with no evident systematic patterns (Fig. 6). The dominant problem of orbit determination for BeiDou GEO and QZSS satellites is threefold: (1) not employing the normal orbit mode by all analysis centers, (2) satellite orbit instability in the geostationary region due to the resonance with earth rotation and gravity field, and (3) no change of the satellite observation geometry for ground-borne receivers.

Fig. 6
figure 6

SLR residuals as a function of satellite elongation angle with respect to the sun position

Full size image

Interestingly, BeiDou-3 CAST and SECM are characterized by opposite patterns of SLR residuals (Fig. 5). CAST satellites have patterns similar to those of elongated GLONASS-M satellites, whereas SECM satellites have patterns similar to those of Galileo satellites suggesting that the Z-bus area with transmitter antennas is much larger than the X-bus surface area and vice versa for CAST. The results agree with the BeiDou-3 metadata released in December 2019, disclosing that the effective surface area for SECM is 2.59 and 1.25 m2 for the Z and X panels, respectively, whereas for CAST, it is 2.18 and 2.86 m2 for the Z and X panels. Figure 6 shows the dependencies of the SLR residuals as a function of the satellite elongation angle with respect to the position of the sun with, again, an opposite pattern for SECM and CAST satellites. The systematic patterns of SLR residuals can greatly be reduced when using the a priori box-wing model based on BeiDou-3 metadata and when estimating phase center correction models (Yan et al. 2019). We may thus conclude that the orbit modeling of all GEO, IGSO, and BeiDou-3 satellites should be improved to eliminate the systematic effects, whereas BeiDou-2 MEO has today acceptable orbit processing strategies for high-accuracy geodetic applications.

Conclusions

The IGS ACC established in 2019 an experimental multi-GNSS orbit combination service by adapting the well-established IGS combination procedures. The multi-GNSS orbits are based on individual products generated by IGS and MGEX analysis centers. The number of included GPS, Galileo, and GLONASS is at a stable level of 32, 24, and 23 satellites, respectively. The number of BeiDou satellites in the combined products varies between 10 and 33 because BeiDou-3 satellites are currently being processed only by one center, whereas the number of considered QZSS satellites varies between 1 and 4.

From the orbit quality assessment based on WRMS of the orbit combination, the 3D mean errors are 9, 15, 16, 24, 37, and 26 mm for GPS, Galileo, GLONASS, BeiDou IGSO and MEO, BeiDou GEO, and QZSS, respectively (Table 2). The mean STD values in the radial direction are 5, 8, 9, 14, 21, and 15 mm for the satellites in the same order. STD of SLR residuals is 23, 29, 40, 51, 87, and 72 mm for Galileo, GLONASS, BeiDou MEO, IGSO, GEO, and QZSS, respectively. In all tests, Galileo turned out to be the system with the highest quality of orbit products out of all new GNSS, which confirms that Galileo is fully suitable for the future realizations of International Terrestrial Reference Systems, such as the International Terrestrial Reference Frame ITRF2020.

Table 2 Summary of the combined orbit quality: SLR residuals and RMS of orbit differences in radial and 3D. All values in mm. GPS Block II includes IIA, IIR, IIR-M, and IIF satellites, GLONASS M+ includes all M+ satellites and R15 in addition
Full size table

We found that GPS III G04 (SVN 74) has combination STD twice as large than other GPS satellites. The GLONASS-M+ satellites (SVNs 855, 856, 858) and R15 (SVN 857) have a large positive SLR bias of + 29 mm. GLONASS-K1 R09 (SVN 802) has the smallest STD of SLR residuals out of all GLONASS satellites, which can be explained by a regular cuboid shape of the satellite bus and a new type of SLR retroreflector arranged in the form of a ring.

Galileo IOVs show large negative SLR residuals when the sun is near perpendicular to the orbital plane. BeiDou-3 SECM and CAST satellites have opposite patterns of SLR residuals when analyzed as a function of the sun elongation angle and the satellite latitude, which means that the construction and surface properties of BeiDou-3 MEO satellites from different manufacturers may be different. The orbit modeling of QZSS, BeiDou-2 GEO, IGSO, BeiDou-3, and GPS III needs enhancement to meet the demand for high-accuracy GNSS products. Interestingly, the smallest bias of just − 1 mm and the STD of SLR residuals of 18 mm were obtained for E14 (SVN 202)—the Galileo satellite that had never been intended to fly in an eccentric orbit. Galileo E12 (SVN 102) also has a very low STD value of SLR residuals of 17 mm. However, the bias for E12 is equal to − 7 mm.

The current combination procedure was optimized to fulfill the needs of the IGS repro3 for the ITRF2020 combination, in which double difference GPS–GLONASS–Galileo solutions will be employed. The combination procedure will be improved in near future by considering a proper clock combination, aligning the orbits with the IGS reference frame, and improving the robustness of the combination for BeiDou-3 as well as GEO and IGSO orbits from the BeiDou and QZSS constellations, which are currently missing in many single-day solutions. All these changes are indispensable for a transition from experimental to the fully operational multi-GNSS combination.