Trade creation and trade diversion of economic integration agreements revisited: a constrained panel pseudo-maximum likelihood approach

Abstract

For PPML estimation of high-dimensional structural gravity panel models it proves useful to exploit the equilibrium restrictions imposed by the system of multilateral resistances. The main advantage of this approach lies in the functional dependence of the parameters of all dummy variables on the structural trade cost parameters. Moreover, the delta method is used to establish confidence intervals of counterfactual changes. Using the constrained panel PPML estimator for a panel of 65 countries in the period 1994–2012 indicates significant trade creation of economic integration agreements with average ranging in between 12.2 and 30.3% in 2012. Results also point to substantial domestic and international trade diversion, where the former dominates the latter.

1 Introduction

The large number of existing economic integration agreements (EIAs) has induced what is called a spaghetti bowl of preferential trade relationships. A myriad of papers assesses the impact of EIAs on bilateral trade and welfare empirically, mainly focusing on the trade creation effects of EIAs. In contrast, evidence on the trade diversion effects of EIAs seems to be more scarce.

The measurement of the trade creating impact of EIAs is typically based on gravity models of bilateral trade and EIA-dummy indicators. Identifying trade diversion effects is less straight forward. Many contributions use a reduced form measuring trade diversion by a dummy variable that picks out trade flows between any two countries that do not share an EIA, but either the exporter country or the importer country (or both) have one or more EIAs in force with other countries.¹ Strictly speaking, in this design trade diversion is modelled as if the conclusion of an EIA between any two countries increases trade barriers toward third non-member countries.

Economic theory predicts the adjustment of the terms of trade and, therefore, multilateral resistances, as a response to the formation of EIAs (Anderson and Yotov 2016). Actually, trade diversion is a consequence of the general equilibrium effects induced by EIAs, but not necessarily of new trade barriers between EIA members vis-à-vis non-EIA members. Contributions by, e.g., Caliendo and Parro (2015), Clausing (2001), Felbermayr et al. (2015) and Trefler (2004) consider specific trade agreements and favour the structural (general equilibrium) approach to estimate the trade creating and trade diverting effects of EIAs, as well as the implied welfare effects. In a similar vein, Bergstrand et al. (2015) estimate the welfare effects of EIAs using a structural gravity model in the spirit of Anderson and van Wincoop (2003). All these models fully account for the changes in terms of trade via changes in the estimated multilateral resistances.

This paper reconsiders the trade creation and trade diversion effects of EIAs using constrained panel PPML estimation and the delta method for establishing reliable confidence intervals of general equilibrium EIA effects. The estimated econometric specification follows Bergstrand et al. (2015), modelling the impact of EIAs on bilateral trade as a reduction of the border effects. In line with the literature, in a sample of 65 mainly developed countries the EIAs put in force between 1994–2012 induced positive and quantitatively important trade creation effects. But despite their increasing number and the phasing-in effects the trade creating effect of EIAs increased only moderately over time. The establishment of EIAs improved the welfare of countries with many EIAs in force, while for those with just a few EIAs in force the welfare gains turned out insignificant.

On the other hand, EIAs produced pronounced and significant trade diversion effects. Since the data base includes domestic trade flows it is possible to compare the diversion of domestic trade flows with that of international trade flows with the outsider countries to EIAs. If the former dominate the latter, the trade diverting repercussions of EIAs are possibly less of a concern for economic policy in the outsider countries. Indeed, the estimation results indicate that on average the diversion of domestic trade turn out substantial and larger than the diversion of international trade with outside countries.

Freezing all trade costs as well as the EIA status counterfactually at the level of 1994 reveals a much lower trade creating effect of EIAs relative to non-policy related changes in trade barriers. A third scenario with all international trade flows counterfactually covered by an EIA indicates potential of welfare gains of further multilateral trade liberalization efforts. This scenario would induce a substantial increase in trade flows not covered by EIAs and sizeable welfare gains of countries holding just a few EIAs, affecting trade flows under existing EIAs only marginally.

Since parameter estimation induces uncertainty to the counterfactual predictions, the involved confidence intervals of the estimated EIA-effects are relatively large and wider than previously reported in the literature, however.

As a methodological contribution, the paper introduces a constrained panel pseudo-Poisson maximum likelihood (PPML) estimation approach, adapting the constrained PPML estimator for cross-sections proposed in Pfaffermayr (2020) to a panel setting. The constrained panel PPML estimator concentrates out country-pair fixed effects and exploits the restrictions imposed by the system of multilateral resistances not only for comparative static analysis, but also for estimation. Since concentrating out country-pair fixed effects is equivalent to imposing further restrictions on the cross-section based constrained PPML estimator, the available econometric results for this estimator are applicable to a panel setting as well.

While both the constrained and the unconstrained panel PPML estimators of the structural trade cost parameters are consistent if the imposed restrictions hold true, there are several important differences. First, Weidner and Zylkin (2019) show that in a three-way panel the unconstrained PPML estimates of the structural trade cost parameters are biased (to the order of the number of countries) as the exporter-time and importer-time dummies are treated as parameters to be estimated.² Thus asymptotic confidence intervals are not correctly centered at the true point estimates. The constrained PPML estimator is free of this asymptotic bias, since exporter-time and importer-time dummies are pinned done by the system of multilateral resistances and are thus functionally dependent on the structural trade cost parameters and the exogenously given gross-production and expenditures figures.

Second, under constrained PPML estimation the estimated standard errors of the structural trade cost parameters typically exhibit a much lower bias (downward and of the order of the number of countries) as demonstrated in Pfaffermayr (2020). Moreover, it is straight forward to apply the delta method to derive confidence intervals for counterfactual predictions which might serve as an alternative to computationally intensive bootstrapping procedures. Constrained panel PPML estimation is especially useful in case of missing trade flows. It implicitly predicts the missing trade flows and delivers theory consistent predictions that add up the given gross production and expenditure figures.

The constrained PPML estimation approach is related to several contributions to the literature. French (2016, 2017) also applies the constrained estimator to gravity models. However, he does not use the constrained PPML estimator to improve inference and to establish confidence intervals of counterfactual predictions. Poissonnier (2019) proposes the usage of the RAS-algorithm used in the input–output literature to solve the system multilateral resistances efficiently. Lastly, the present paper contributes to the evolving literature proposing fast zig–zag algorithms for the estimation of high dimensional panel models based pseudo-demeaning or separate up-dating of fixed effects (see Correia et al. 2020; Larch et al. 2019; Stammann 2018).

2 The structural panel gravity model

For $C^{2}$ country-pairs observed over T periods bilateral trade flows from country i to j in period t denoted by $X_{ijt}$ are assumed to be generated by a generic gravity model (see Allen et al. 2020) as

$$\begin{aligned} \tfrac{X_{ijt}}{Y_{t,W}}=t_{ijt}^{1-\sigma }\kappa _{it}\Pi _{it}^{\sigma -1}P_{jt}^{\sigma -1}\theta _{jt}e^{\mu _{ij}}\eta _{ijt}\equiv e^{z_{ijt}^{\prime }\alpha +\beta _{it}(\alpha ,\mu )+\gamma _{jt}(\alpha ,\mu )+\mu _{ij}}\eta _{ijt}. \end{aligned}$$

(1)

Bilateral trade flows are normalized by world expenditures denoted by $Y_{t,W}$ so that $\sum _{i=1}^{C}\sum _{j=1}^{C}s_{ijt}=1$, where $s_{ijt}= \tfrac{X_{ijt}}{Y_{t,W}}$. $t_{ijt}$ denotes the index of time varying trade frictions (in many theoretical models the iceberg transportation costs) and $1-\sigma$ the trade elasticity. The econometric specification uses the parametrization $t_{ijt}^{1-\sigma }=e^{z_{ijt}^{\prime }\alpha +\mu _{ij}}$ , where the vector $z_{ijt}$ comprises the ijt-specific observations on trade friction indicators with corresponding parameter vector $\alpha$. These are the parameters to be estimated and referred to as the structural trade cost parameters. Country-pair fixed effects, $\mu _{ij}$, capture time invariant unobserved bilateral barriers to trade. It is assumed that $z_{ijt}$ is observed for all country pairs and all periods, while some trade flows may be missing at random. However, for each country pair trade flows have to be observed at least twice in order to ensure that country-pair fixed effects can be estimated.

$\kappa _{it}$ denotes the share of country i’s gross production in world expenditures, while $\theta _{jt}$ refers to country j’s expenditure share in world expenditures. $\kappa _{it}$ and $\theta _{jt}$ may differ from each other, so the gravity model allows for trade imbalances at the country level. For estimation, the countries’ production and expenditure figures are assumed to be exogenously given.

Multilateral resistances are denoted by $\Pi _{it}^{\sigma -1}$ and $P_{jt}^{\sigma -1}$, respectively, and enter the econometric model in normalized form as exporter-time and importer-time specific parameters defined as $\kappa _{it}\Pi _{it}^{\sigma -1}\equiv e^{\beta _{it}(\alpha ,\mu )}$ and $\theta _{jt}P_{jt}^{\sigma -1}\equiv e^{\gamma _{jt}(\alpha ,\mu )}$. For $i,j=1,\ldots ,C$ and period t the system of multilateral resistances can then be compactly written as

$$\begin{aligned} \kappa _{it}= & {} \sum _{j=1}^{C}e^{z_{ijt}^{\prime }\alpha +\beta _{it}(\alpha ,\mu )+\gamma _{jt}(\alpha ,\mu )+\mu _{ij}},\text { }i=1,\ldots ,C-1 \end{aligned}$$

(2)

$$\begin{aligned} \theta _{jt}= & {} \sum _{i=1}^{C}e^{z_{ijt}^{\prime }\alpha +\beta _{it}(\alpha ,\mu )+\gamma _{jt}(\alpha ,\mu )+\mu _{ij}},\text { }j=1,\ldots ,C \end{aligned}$$

(3)

Hence, $\beta _{it}(\alpha ,\mu )$ and $\gamma _{jt}(\alpha ,\mu )$ are fully determined by the equilibrium restrictions of the gravity model and are not parameters that need to be estimated. The normalized multilateral resistance terms depend on the vector of structural trade cost parameters $\alpha$, the country-pair fixed effects $\mu _{ij}$, the gross production and expenditure shares of the countries and on the number of countries in the sample. Thus the data generating process (DGP) of $s_{ijt}$ changes with the number of countries and $s_{ijt}$ forms a triangular array.³

In general, the solutions of the system of trade resistances are unique up to a constant and the multilateral resistances have to be normalized. Here, the restriction $\beta _{Ct}=0,$ $t=1,\ldots ,T$ is imposed. Furthermore, the country-pair fixed effects need to be normalized as well to obtain a full rank dummy design matrix for the multilateral resistances. Actually, in this three-way model only $(C-1)^{2}$ country-pair effects are identified in the presence of the full set of exporter-time and importer-time effects. The reason is that the exporter-time and importer-time share the same base as the bilateral fixed effects, namely the $2C-1$ exporter and importer fixed effects. Since the full set of exporter-time and importer-time fixed effects is included to obtain estimates of all multilateral resistance terms, $2C-1$ bilateral fixed effects have to be skipped and set to 0. This leaves $C^{2}-2C+1$ identifiable bilateral fixed effects. Without loss of generality one may set $\mu _{ii}=0$ and $\mu _{Cj}=0,$ $i,j=1,\ldots ,C.$ This normalization also implies that there is no constant in the model and without further structural assumptions on the DGP the value of world expenditures remains unspecified.

Lastly, the disturbances $\eta _{ij}$ enter multiplicatively with $E[\eta _{ijt}|z_{ijt}]=1$ and can be heteroskedastic or clustered in the country-pair dimension. Santos Silva and Windmeijer (1997) demonstrate that in a PPML or a method of moments framework with exogenous explanatory variables the models with multiplicative and additive disturbances are observationally equivalent and lead to the same estimators, since they are based on the same conditional mean assumptions. Under IV-estimation, this equivalence breaks down, however.

For estimation the structural gravity model can be reformulated in an abbreviated notation with additive disturbances

$$\begin{aligned} s_{ijt}=m_{ijt}(\vartheta )+\varepsilon _{ijt},\quad \varepsilon _{ijt}=m_{ijt}(\vartheta )\left( \eta _{ijt}-1\right) , \end{aligned}$$

(4)

where $m_{ijt}(\vartheta )=e^{z_{ijt}^{\prime }\alpha +\beta _{it}(\alpha ,\mu )+\gamma _{jt}(\alpha ,\mu )+\mu _{ij}}$, $\vartheta =[\phi (\alpha ,\mu )^{\prime },\mu ^{\prime }]^{\prime },$ $\phi (\alpha , \mu ) =[\alpha ^{\prime },$ $\beta ^{\prime }(\alpha ,\mu ),$ $\gamma ^{\prime }(\alpha ,\mu )]^{\prime }$.

3 The econometrics of constrained panel PPML estimation

3.1 The constrained panel PPML estimator

The proposed constrained panel PPML estimator exploits the restrictions imposed by the system of multilateral resistances and maximizes the conditional Poisson likelihood under the constraints (2) and (3). This estimation procedure concentrates out country-pair fixed effects and implicitly predicts all missing trade flows when solving the system of multilateral resistances. As shown in the Technical "Appendix, Sect. 1" maximizing the conditional Poisson likelihood under the constraints (2) and (3) is equivalent to applying the constrained unconditional PPML estimator for cross-sections as analyzed in Pfaffermayr (2020), imposing the additional restrictions $\sum _{t=1}^{T}v_{ijt}m_{ijt}(\vartheta )=$ $\sum _{t=1}^{T}v_{ijt}s_{ijt}$ for all country pairs with non-zero $\mu _{ij}$.⁴ Thereby, $v_{ijt}$ is an indicator variable taking the value 1 if $s_{ijt}$ is observed and zero otherwise. Missingness has to occur at random for the panel PPML estimators to be consistent. The introduction of these additional restrictions is for convenience as it allows to apply the results in Pfaffermayr (2020) to establish the asymptotic distribution of the structural trade cost parameters ${\widehat{\alpha }}$.

For estimation one may apply an iterative, constrained, projection based estimation procedure similar to that put forward in Falocci et al. (2009). For cross-section gravity models it is described in detail in Pfaffermayr (2020) and for panels in Technical "Appendix 1.2". It is useful to define the following vectors and matrices, the index r indicates the r-th iteration step.

$$\begin{aligned} {\widehat{m}}_{ijt,\phi ,r}=\, & {} e^{z_{ijt}^{\prime }{\widehat{\alpha }}_{r}+\beta _{it}({\widehat{\alpha }}_{r},{\widehat{\mu }}_{r})+\gamma _{jt}(\widehat{\alpha }_{r},{\widehat{\mu }}_{r})},\text { }{\widehat{\pi }}_{ij,r}=e^{{\widehat{\mu }} _{ij,r}},\nonumber \\ {\widehat{M}}_{\phi ,r}=\, & {} diag({\widehat{m}}_{ijt,\phi ,r} )\text {, } {\widehat{M}}_{r}=diag({\widehat{m}}_{ijt,\phi ,r}{\widehat{\pi }}_{ij,r}) \nonumber \\ {\widehat{Q}}_{\mu ,r}=\, & {} I_{TC^{2}}-{\widehat{M}}_{r}VD_{\mu }\left( D_{\mu }^{\prime }V{\widehat{M}}_{r}D_{\mu }\right) ^{-1}D_{\mu }^{\prime } \nonumber \\ {\widehat{G}}_{r}=\, & {} W_{\phi }^{\prime }{\widehat{Q}}_{\mu ,r}V{\widehat{M}} _{r}W_{\phi },\text { }{\widehat{F}}_{r}=D_{\phi }^{\prime }{\widehat{M}}_{r} {\widehat{Q}}_{\mu ,r}W_{\phi }, \end{aligned}$$

(5)

where ${\widehat{G}}_{r}$ is assumed to be non-singular. The $C^{2}T\times (C-1)^{2}$ design matrix $D_{\mu }$ refers to country-pair dummies and $D_{\phi }$ denotes the $C^{2}T\times \left( 2C-1\right) T$ design matrix for the exporter-time and importer-time dummies. Further, $W_{\phi }=[Z,D_{\phi }]$ and V is a diagonal matrix with typical element $v_{ijt}.$ Lastly, we define the $\left( 2C-1\right) T$ vector $\theta _{\phi }$ = ($\kappa _{11},\ldots ,\kappa _{C-1,T},\theta _{11},\ldots ,\theta _{CT})^{\prime }$ and collect the country-pair specific trade flow averages in $\theta _{\mu }$ (a $(C-1)^{2}$ vector with typical element $\mu _{ij}$).⁵ Remember, $\phi =[\alpha ^\prime ,\beta ^\prime ,\gamma ^\prime ]^\prime$.

Given iteration r, iteration step $r+1$ proceeds with the following calculations:

• 1. ${\widehat{\phi }}_{r+1}={\widehat{\phi }}_{r}+\left( {\widehat{G}}_{r}^{-1}- {\widehat{G}}_{r}^{-1}{\widehat{F}}_{r}^{\prime }\left( {\widehat{F}}_{r}\widehat{G }_{r}^{-1}{\widehat{F}}_{r}^{\prime }\right) ^{-1}{\widehat{F}}_{r}{\widehat{G}} _{r}^{-1}\right) W_{\phi }^{\prime }V(s-{\widehat{m}}_{r})$ $+{\widehat{G}}_{r}^{-1}{\widehat{F}}_{r}^{\prime }\left( {\widehat{F}}_{r} {\widehat{G}}_{r}^{-1}{\widehat{F}}_{r}^{\prime }\right) ^{-1}\left( \theta _{\phi }-D_{\phi }^{\prime }{\widehat{m}}_{r}\right)$

• 2. ${\widehat{\pi }}_{r+1}=(D_{\mu }^{\prime }VM_{\phi }({\widehat{\phi }}_{r+1} )D_{\mu })^{-1}D_{\mu }Vs$

• 3. Calculate ${\widehat{m}}_{r+1}$, $M({\widehat{\phi }}_{r+1}, {\widehat{\pi }}_{r+1})$, ${\widehat{Q}}_{\mu ,r+1},$ ${\widehat{G}}_{r+1},{\widehat{F}} _{r+1}$ and iterate until convergence.

Step 1 of this procedure projects out exporter-time and importer-time effects based on all observations (i.e., including also those with missing trade flows in forming the projection matrix). It weighs deviations of the score from zero against violations of the restrictions when updating the parameter vector ${\widehat{\phi }}_{r}$. Step 2 calculates the country-pair fixed effects separately, given the estimates of the remaining parameters ${\widehat{\phi }}_{r+1}$. This step avoids the inversion of large matrices arising from the inclusion of country-pair dummies.

This iterative constrained panel PPML estimation procedure is very similar to that for the cross-sections. The only difference is the usage of the projection matrix ${\widehat{Q}}_{\mu ,r}$ to eliminate the country-pair fixed effects in step 1 and the intermediate step 2 to estimate ${\widehat{\pi }} _{r+1}$. Starting values may come from unconstrained panel PPML estimators. Since unconstrained PPML is often based on different dummy designs and normalizations, one can use the estimated structural trade cost parameters ${\widehat{\alpha }}_{1}$ obtained from unconstrained panel PPML with exporter-time and importer-time dummies, but start with the solution of the system of multilateral resistances at $\alpha =0$, i.e., ${\widehat{\phi }} _{1}$ $=({\widehat{\alpha }}_{1}^{\prime },\theta _{\phi }^{\prime })^{\prime }$ and calculate, ${\widehat{\pi }}_{1}$ as in step 2.

The first order conditions of the constrained panel PPML estimator are identical to those of the cross-sectional constrained PPML, so the results in Pfaffermayr (2020) apply to establish the limit distribution of $CT^{ \frac{1}{2}}({\hat{\alpha }}-\alpha _{0})$. In fact, this proposition assumes that the imposed restrictions hold under the DGP and it states that under a set of regularity conditions and independent, but heteroskedastic disturbances, the constrained panel PPML estimator ${\widehat{\alpha }}$ is consistent and asymptotically normal with

$$\begin{aligned} CT^{\frac{1}{2}}({\widehat{\alpha }}-\alpha _{0})\overset{d}{\rightarrow } N\left( 0,B_{0}^{-1}A_{0}\Omega _{\varepsilon }A_{0}^{\prime }B_{0}^{-1}\right) , \end{aligned}$$

(6)

where $A_{0}\Omega _{\varepsilon }A_{0}^{\prime }=p\lim _{C\rightarrow \infty }\frac{ 1}{C^{2}T}A(\alpha ^{*})\varepsilon \varepsilon ^{\prime }A(\alpha ^{*})^{\prime },$ $B_{0}=p\lim _{C\rightarrow \infty }B(\alpha ^{*}),$ with $\alpha ^{*}$ lying in between those of ${\widehat{\alpha }}$ and $\alpha _{0}$, element by element and

$$\begin{aligned} A(\alpha )= & {} C^{2}TZ^{\prime }(I_{TC^{2}}-M(\alpha )D^{\prime }\left( F(\alpha )G(\alpha )^{-1}F(\alpha )^{\prime }\right) ^{-1}F(\alpha )G(\alpha )^{-1}W^{\prime })V \nonumber \\ B(\alpha )= & {} Z^{\prime }V\left( M(\alpha )-M(\alpha )D(D^{\prime }M(\alpha )D)^{-1}D^{\prime }M(\alpha )\right) Z, \end{aligned}$$

(7)

where $M(\alpha )=diag(m_{ijt}(\alpha )),$ $G(\alpha )=W^{\prime }VM(\alpha )W$ and $F(\alpha )=D^{\prime }M(\alpha )W$, respectively. Since $\widehat{ \alpha }$ is consistent, it can be plugged in (7) and one may use $\frac{1}{C^{4}T^{2}}B({\widehat{\alpha }})^{-1}A({\widehat{\alpha }})diag( {\widehat{\varepsilon }}{\widehat{\varepsilon }}^{\prime })A({\widehat{\alpha }} )^{\prime }B({\widehat{\alpha }})^{-1}$ for inference in finite samples. The normalization differs from the standard approach as $m_{ijt}(\alpha )$ and $E(\varepsilon _{ij}^{2})$ are assumed to be $O(C^{-2})$ and $o_{p}(C^{-4})$, respectively, to account for the normalization of trade flows by world expenditures. A detailed comparison of the unconstrained and constrained PPML estimators is given in Pfaffermayr (2020).

If the disturbances are correlated within country pairs, e.g. due to serial correlation, it is important to cluster standard errors along this dimension. The corresponding selection matrix picks out $C^{2}$ country-pair clusters and can be defined as $D_{\mu }D_{\mu }^{\prime }.$ Then one obtains

$$\begin{aligned} A_{0}\Omega _{\varepsilon }A_{0}^\prime =p\lim _{C\rightarrow \infty }\tfrac{1}{C^{2}T }A(\alpha ^{*})\left( \varepsilon \varepsilon ^{\prime }\circ D_{\mu }D_{\mu }^{\prime }\right) A(\alpha ^{*})^\prime , \end{aligned}$$

(8)

where $\circ$ denotes the Hadarmard element-wise product.

3.2 The asymptotic distribution of counterfactual predictions

The delta method allows to derive the asymptotic distribution of counterfactual predictions for aggregates or finite subsets of bilateral trade flows. Thereby, the selection matrix R picks out a finite set of country pairs and aggregates them accordingly. The rank of R has to be smaller than the number of the estimated structural parameters. Let superscript c denote counterfactuals arising from changes in trade barriers from Z to $Z^{c}$. Matrices without superscript refer to the baseline. The delta method uses the derivatives

$$\begin{aligned} \Upsilon _{0}^{c}= \,& {} RM^{c}(\alpha _{0})^{-1}M(\alpha _{0})\left[(I_{TC^{2}}-D_{\phi }\left( D_{\phi }^{\prime }M^{c}(\alpha _{0})D_{\phi }-H(\alpha _{0})\right) ^{-1}D_{\phi }^{\prime }M^{c}(\alpha _{0}))Z^{c} \right.\\&\left.+D_{\phi }\left( D_{\phi }^{\prime }M^{c}(\alpha _{0})D_{\phi }-H(\alpha _{0})\right) ^{-1}H(\alpha _{0})\left( D_{\phi }^{\prime }M(\alpha _{0})D_{\phi })\right) ^{-1}D_{\phi }^{\prime }M(\alpha _{0})Z\right] \\ \ \Upsilon _{0}=\, & {} RM^{c}(\alpha _{0})^{-1}M(\alpha _{0})\left[I_{TC^{2}}-D_{\phi }\left( D_{\phi }^{\prime }M(\alpha _{0})D_{\phi }\right) ^{-1}D_{\phi }^{\prime }M(\alpha _{0})\right]Z, \end{aligned}$$

where $RM^{c}(\alpha _{0})^{-1}M(\alpha _{0})$ has typical non-zero diagonal element

$$\begin{aligned} e^{(z_{ijt}-z_{ijt}^{c})^{\prime }\alpha +\beta _{it}(\alpha ,\mu )+\gamma _{jt}(\alpha ,\mu )-\beta ^{c} _{it}(\alpha ,\mu )-\gamma ^{c} _{jt}(\alpha ,\mu )} \end{aligned}$$

and the fixed county-pair effects, $\mu _{ij}$, are treated as given. The matrix $H(\alpha _{0})$ accounts for the change of gross production and expenditures in full general equilibrium, which are specified as $\kappa ^c_{it}=\tfrac{\pi ^c _{it}}{\sum _{k=1}^{C}\pi ^c _{kt}}$, $\pi _{it}^c=e^{\frac{\beta _{it}^c(\alpha ,\mu )-\beta _{it}(\alpha ,\mu )}{1-\sigma }}\kappa _{it}$, and $\theta ^c _{jt}=\kappa _{jt}^c\tfrac{\theta _{jt}}{\kappa _{jt}}$, respectively.⁶

Under a standard set of regularity conditions, one can conjecture that

$$\begin{aligned}&CT^{\frac{1}{2}}R\left( M^{c}({\widehat{\alpha }})^{-1}m({\widehat{\alpha }} )-M^{c}(\alpha _{0})^{-1}m(\alpha _{0})\right) \nonumber \\&\overset{d}{\rightarrow }N\big (0,\left( \Gamma _{0}-\Gamma ^{c} _{0}\right) V_{\alpha }\big ( \Gamma _{0}-\Gamma ^{c} _{0}\big ) ^{\prime }\big ), \end{aligned}$$

(9)

where $V_{\alpha }=B_{0}^{-1}A_{0}\Omega _{\varepsilon }A_{0}^{\prime }B_{0}^{-1}$, $\Gamma _{0}^{c}=\lim _{C\rightarrow \infty }\Upsilon _{0}^{c}$ and $\Gamma _{0}=\lim _{C\rightarrow \infty } \Upsilon _{0}$. Furthermore, $\big ( {\widehat{\Upsilon }}-{\widehat{\Upsilon }}^{c}\big ) -\left( \Upsilon _{0}-\Upsilon _{0}^{c}\right) =o_{p}(1).$ The Monte Carlo simulations provided below confirm this result. The estimates of counterfactual changes and their standard errors likewise remain unaffected by the nuisance parameters $\mu _{ij}$ and by the dummies for the multilateral resistance terms as these are fully determined by the set of constraints at given $\alpha$ and projected out.

3.3 A small scale Monte Carlo study

A small scale Monte Carlo analysis compares the performance of the constrained and unconstrained PPML estimators with respect to the estimated structural trade cost parameters and counterfactual changes in predicted trade flows. As an alternative to the delta method, the simulation experiments also consider parametric bootstraps for the counterfactual predictions following Larch and Wanner (2017) and Felbermayr et al. (2018). The bootstrap procedure uses 500 draws from the asymptotic normal distribution of the estimated structural trade cost parameters.

The simulations are based on a set of 20 countries observed over 4 periods (1997, 2000, 2003, 2006) using the same database as the empirical analysis below. The estimated model includes a border dummy and log distance, both interacted with time dummies for 2000, 2003 and 2006, as well as an EIA dummy. The true slope parameters and the country-pair fixed effects are taken from an initial panel PPML regression with fixed country-pair, exporter-time and importer-time effects. The true multilateral resistance parameters are then derived as solutions of the corresponding system of multilateral resistance equations.

Disturbances with full support on ${\mathbb {R}}$ may lead to negative trade flow realizations. For this reason independent disturbances are generated from a truncated normal distribution with standard deviation of 0.0222 support $[-0.0394,0.0394]$. The disturbances follow an AR(1) process with parameter 0.2 so that there is correlation within units, but independence across units is preserved. The disturbances enter the true model multiplicatively (adding 1 to the generated disturbances) so that a model estimated under the assumption of additive disturbances is heteroskedastic (see Eq. 4). Under this data generating process one obtains t-values for the estimated slope parameters that are comparable to those usually found for estimated gravity models.⁷

The simulations are conducted for the fully observed panel as well as for an unbalanced panel with 50% of the observations missing in the last two periods. The first two waves of trade flows are fully observed to guarantee that country-pair fixed effects can be derived from at least two country-pair observations. All Monte Carlo experiments use standard errors clustered by country pair and are based on 2000 replications. Since the Monte Carlo simulations themselves add noise, the simulated coverage ratios have to be compared to their $95\%$-confidence intervals amounting to [0.940, 0.960].

Table 1 reports simulated bias, standard errors and the coverage rates of the confidence intervals of the estimated EIA-parameter and, as an example, the estimated average trade diversion effects in the last period, which amounts to $-2.46$% under the true model. The calculation of the corresponding welfare effects follows Arkolakis et al. (2012) and assuming $\sigma =6.982$, the true average welfare effect amounts to 0.6%.

Table 1 Monte Carlo simulation results: simulated standard errors and coverage rates of the estimated EIA parameter and counterfactual predictions under unconstrained and constrained panel PPML estimation

The bias of the estimated EIA parameter is negligible for both the unconstrained and the constrained PPML-estimator. This result is in line with the results of Weidner and Zylkin (2019), who argue that under a log-homoskedastic DGP, as assumed here, positive and negative bias terms mitigate one another. Under constrained PPML estimation the estimated standard error of the EIA parameter estimate comes close to its simulated counterpart. Its bias, defined as the ratio of estimated standard error and its simulated counterpart, amounts to 0.97 in case of 50% missings and to 0.96 in case of a fully observed panel. As a result coverage rates of a $95\%$-confidence interval lie within or very close to the bounds of the $95\%$- simulation confidence interval of [0.940, 0.960]. In contrast, but in line with findings of Pfaffermayr (2019) there is a pronounced downward bias of estimated standard errors under unconstrained PPML estimation (0.47 with no missings and 0.57 with 50% missings). The coverage rates of the $95\%$-confidence intervals substantially deviate from their nominal value and the length of the 95%-confidence intervals reported in the last column of Table 1 turns out substantially smaller.

Constrained PPML estimates do not necessarily lead to efficiency gains, since the moments are not properly weighted under PPML estimation. Under fully observed trade flows the simulated standard error of the EIA parameter is approximately the same under constrained and unconstrained estimation. But under constrained estimation and in case of 50% missing trade flows it turns out larger. To some extent this may be artefact of the design, since 30 out of 36 new EIAs in the data are conducted in the last period, where per design 50% of the trade flows are missing.

As compared to bootstrapping the delta method is computationally much less time-consuming, but naturally affected by approximation error. Under fully observed trade flows, the bias of the standard error of international trade diversion effect is 0.92, and that of the bootstrapped one is 0.97. These moderate biases are reflected in correct coverage rates in both cases. The bootstrapped standard errors under unconstrained PPML estimation inherit the biased standard errors of the structural trade cost parameters so that coverage rates are too small as well. The findings for the welfare effects are very similar and under missing trade flows essentially the same pattern is observed.

Overall, the delta method seems to be a viable alternative to bootstrapping in the present setting. However, though asymptotically valid, the delta method does not always work well in small samples, especially if the variance of the estimated structural trade cost parameters is large and a highly nonlinear function of the parameters is involved (see Hole 2007; Krinsky and Robb 1991 for a detailed comparison in other contexts).

4 Evidence on trade creation and trade diversion

4.1 The econometric specification of the structural gravity model

The specification of the gravity model closely follows Bergstrand et al. (2015), Borchert and Yotov (2017) and Dai et al. (2014), who argue that the structural gravity model is able to identify the cost of international trade relative to domestic trade costs if the database includes domestic trade flows from country i into i itself. Further, in a panel setting with data exhibiting variation over time, the gravity model can be estimated with country-pair fixed effects to control for unobserved time invariant determinants of barriers to trade and to guard against the endogeneity of EIA indicators as observed in cross-sections (see Baier and Bergstrand 2007).⁸

The econometric specification of the structural gravity model accounts for secular globalisation trends as described in Yotov (2012) and Borchert and Yotov (2017). Specifically, it includes border dummies $B_{ij}$, taking the value 1 if $i\ne j$ and 0 else, that are interacted with time dummies $T_{t}$ (with exception of the first period) to measure the change of border effects over time. The evolution of the border effects may differ for more distant trading partners and for non-neighbouring countries. Hence, the border-year effects are additionally interacted with $\ln dist_{ij}$ and the $no-contiguity_{ij}$ dummy, the latter taking the value 1 if country pairs do not share a common border.

EIAs reduce tariffs and possibly also non-tariff barriers to international trade, but by definition do not directly affect domestic trade. So conceptually, EIAs may be thought of yet another determinant that reduces border effects. For this reason the EIA-dummy is likewise interacted with the border dummy. Following Bergstrand et al. (2015) the EIA-indicator enters with 5 and 10 year lags to account for phasing-in of EIAs and sluggish adjustment of trade flows over time.

This specification of the gravity model identifies the change of border effects and the impact of other trade barriers over time, but not that of their initial level, which is absorbed by the country-pair fixed effects. The design allows a clean measurement of the change of the impact of trade barriers on bilateral trade over time, since domestic trade flows serve as the base and are fully described by the country-pair fixed effects and the multilateral resistance terms. To summarize, the basic specification of the gravity equation reads as

$$\begin{aligned} s_{ijt}= & {} \exp \left( \sum _{\tau =2}^{7}\alpha _{1,\tau }B_{ij}T_{\tau }+\alpha _{2,\tau }B_{ij}T_{\tau }\ln (dist_{ij})+\alpha _{3,\tau }B_{ij}T_{\tau }no- contiguity_{ij}\right) \nonumber \\&*\exp \left( \sum _{\tau =0}^{2}\alpha _{4,\tau }B_{ij}EIA_{ij,t-5\tau }+\mu _{ij}+\beta _{it}+\gamma _{jt}\right) +\varepsilon _{ijt}, \end{aligned}$$

(10)

where the restrictions $\beta _{Ct}=0$ and $\mu _{Cj}=\mu _{jj}=0$, $j=1,\ldots ,C$ as well as (3) and (4) are imposed.

4.2 Data and estimation results

The empirical analysis concentrates on trade in manufactured goods. Besides bilateral trade flow data, it uses unilateral data on the value of gross production, total exports and total imports of aggregate manufacturing industries to establish comparable trade flows for domestic trade. In line with the econometric specification trade flows, gross production and expenditures are normalized by world production and in a given year sum up to 1.

The database includes 65 exporter and importer countries and is described in detail in Technical "Appendix, Sect. 3". Bilateral trade flow data come from OECD’s STAN database and Nicita and Olarreaga’s (2007) database, covering the period 1994–2012 in three-year intervals. Data on gross production, total exports and total imports are collected from several sources (OECD-STAN, UNIDO, CEPII and WIOD). Gross production and expenditures shares are corrected for trade with the rest of the world. Moreover, expenditures are adjusted for country specific trade imbalances. In this database the trade flows of a single country approximately, but not exactly, add up to its gross production and to its expenditures, respectively. This adding-up property is violated, because of missing trade flows and measurement errors in the trade flow data generating the unobserved random disturbances.

The sample includes 29, 575 observations, 133 of them had to be skipped because of missing trade flows in all periods. 2219 country-pair observations refer to missing trade flows. Thereby, 14 domestic trade flows have been set to missing because the sum of all trade flows over the 65 countries (including the domestic trade flows) and gross production (corrected for the rest of the world) deviated by more than 30%. Note in OECD’s STAN database zero and missing trade flows are indistinguishable.

Lastly, population weighted geographical distances and the dummy for no-contiguity are taken from Mayer and Zignago (2011), while the information on EIAs is provided by Mario Larch’s Regional Trade Agreements Database described in Egger and Larch (2008). The EIA-dummy takes the value 1 if either a customs union or a free trade area has been established and zero otherwise.

Tables 2 and 3 provide an overview on the descriptive statistics and the most important stylized facts. In 1994 80.5% of total trade referred to domestic trade and this figure has been reduced by 12.9 percentage points until 2012. As of 2012, 42.6% of the trade flows are covered by EIAs covering 18.3% of total trade, while in 1994 these figure amounted to 24.8% and 10.2%, respectively. The median number of EIAs in force per country is 22 and the maximum number is 48. In 1994 8 countries did not participate in any EIA, while 2012 there was only one single country without any EIA.

Table 2 Descriptive statistics I

Table 3 Descriptive statistics II: distribution of trade flows

Table 4 reports the estimation results of the unconstrained and constrained panel PPML estimates of (10), the preferred specification. An assessment of the robustness of the estimation results for different specifications is provided in the Technical "Appendix, Sect. 4".

The constrained PPML estimates indicate a pronounced reduction in the estimated border effects during 1994–2012, amounting to an average yearly decrease of $100(e^{(1.08-0.5*0.18^2)/18}-1)=6.0$%,⁹ which is somewhat higher than that reported by Bergstrand et al. (2015). This reduction in border effects is significantly reinforced for non-neighbouring trading partners during the period 2003–2009, but not in the periods before and after. There is no evidence of a fading role of distance as a barrier to trade (i.e., for reducing border effects) once it is controlled for the change of border effects and no-contiguity over time as is also found in Bergstrand et al. (2015). To the contrary, border effects for more distant countries have been increasing in the years 2000–2009 all else equal.

Table 4 Unconstrained and constrained PPML estimation results of the preferred specification

In line with the literature, the estimated impact of EIAs on bilateral trade flows points to an economically important and significant direct trade enhancing effect of EIAs with pronounced phasing-in patterns. 10 years after putting an EIA into force the direct impact of EIAs accumulates to an increase of bilateral trade flows of $100*(e^{0.37-0.5*0.08^2}-1)=44.3$%, an estimate at the lower end of those available in the literature (see Head and Mayer 2014).

While both the unconstrained and constrained PPML estimators are consistent if the imposed system of multilateral resistances actually holds in the data, in empirical applications important differences between the two estimators do emerge.

First, there is a loss of fit when imposing constraints increasing the in-sample root mean square prediction error from 0.75 to 1.28. Data may not fully support the restrictions imposed by the system of multilateral resistances in the sense that the violations of these adding-up constraints are purely random. If these constraints are violated with the data at hand the estimation results of constrained PPML will be inconsistent, while its unconstrained counterpart is still consistent.

Since there are missing trade flows, the violation of the constraints cannot be checked directly. However, Table 2 indicates that for exporter countries and importer countries with non-missing trade flows the violation of the adding-up constraints is moderate. For those countries trade flows aggregated over importers for each year deviate from gross production by $-1.74$% on average. For trade flows aggregated over exporters-years the average deviation from expenditures amounts to $-0.83$%. In both cases the standard deviation is 6 percentage points. However, there are 544 out of 910 country-time specific trade flow-aggregates (i.e., equations of the system of multilateral resistances) with some trade flows missing, leading to differences between the constrained and unconstrained panel PPML parameter estimates, specifically the exporter-time and importer-time dummies, and thus of the predicted trade flows.

Second, the results of Weidner and Zylkin (2019) imply that the unconstrained PPML estimator of the structural trade cost parameters is possibly biased in finite samples, while the constrained PPML estimator remains unaffected if the imposed constraints are supported by the DGP. As shown in the last two columns of Table 4 the significant parameters estimated by unconstrained PPML are all smaller, on average by $-14.92$%. For the significant EIA parameters, the average difference amounts to $-18.61$%. Moreover, Table 4 indicates that under unconstrained PPML estimation the (out-of-sample) predictions do not add-up exactly to gross production and expenditures, respectively, and thus do not reproduce the baseline equilibrium. Aggregating the out-of-sample predictions over exporting countries for each period leads to values that are lower than gross production by 3.73% on average. Aggregating over importers, the corresponding figure amounts to − 4.11%. While these differences are moderate, the standard deviation in the exporter-time and importer-time dimension amounts to 11.91 and 17.87 percentage points, respectively, indicating large deviations for some countries.

Third, the comparison of the estimated standard errors of the constrained and the unconstrained PPML estimators is not straight forward. The constrained PPML estimator does not weight the moments and is not necessarily more efficient than its unconstrained counterpart. So the true standard errors of the estimated structural trade cost parameters could be, but need not be, smaller. On the other hand, the estimated standard error of the unconstrained PPML estimator tend be downward biased due the estimation of the many exporter-time and import-time dummies as shown in Pfaffermayr (2019) and Weidner and Zylkin (2019). The last column of Table 4 indicates that under unconstrained PPML estimation the estimated standard errors are smaller by an average margin of 19.8%, those of the estimated EIA parameters by 9.8%.

Section 4 of Technical "Appendix" reports several robustness checks for alternative specifications. First, it is possible to include additional country-specific control variables that are interacted with borders.¹⁰ As emphasized by Heid et al. (2017) the impact of unilateral trade policies is identified if domestic trade flows are observed. Yet, it is only possible to include these variables either for exporters or importers, but not for both. Following Cárrere et al. (2013) real GDP per capita may be seen as a good indicator of the quality of transportation infrastructure. In addition, the index on democracy provided by Polity IV has been included. Both variables enter as interaction with the border dummy and are either included as exporter-time varying variables or as importer-time variables. The explanatory power of the Polity IV indicator is rather low. With respect to real GDP per capita the constrained PPML estimation results turn out to be sensitive and the estimated coefficient differs substantially from its unconstrained counterpart. However, the estimated EIA effect remains robust. The second robustness exercise introduces 3 year lags for EIAs to reconcile the phasing-in effects with the frequency of 3 year periods of the panel. Using lag 3, 6 and 9 instead 5 and 10 yields a direct impact of the EIAs on bilateral trade flows of 0.37, similar in size as under the baseline specification. Lastly, skipping the contemporaneous EIA dummy to further guard against endogeneity concerns does not change the estimated total effects of EIAs either.

4.3 Counterfactual predictions

The counterfactual predictions of the impact of EIAs on trade and welfare are based on the estimation results of Table 4. Besides considering trade creation effects of EIAs, the counterfactual analysis takes a closer look at possible trade diversion effects and their structure. Specifically, it compares the trade diversion effects coming from a reduction of internal trade with those originating from a reduction of international trade of EIA members with countries outside the EIAs. If the former dominate the latter, the trade diverting repercussions of EIAs are possibly less of a concern for economic policy of outsider countries.

While analytical results on the structure of the trade diversion effects cannot be established in general due to the non-linearity of the system of multilateral resistances, it is possible to investigate this issue in a small scale simulation exercise. The results of such a simulation exercise for an endowment economy a la Anderson and van Wincoop (2003) are reported in Table 5. The endowments of 20, 40 and 60 countries, respectively, are randomly drawn from a right skewed distribution ($\chi ^2(1)$). International trade costs are generated as $t_{ij}=1+((max(\tau _{ij})-\tau _{ij})/max(\tau _{ij}))$, where $\tau _{ij}$ is assumed to be distributed as $\chi ^2(15)$. The distribution of trade costs is left skewed and bounded in the interval [1,2]. Domestic trade costs are normalized to 1. The counterfactual experiment removes the barriers to trade between the second (labelled country 2) and third (labelled country 3) largest countries, whose bilateral trade costs are set to 1.8 trough out. In each simulation run the structural gravity model is solved to establish the general equilibrium effects of this trade cost reduction so that each country’s gross production and expenditures adjust endogenously.

The simulation exercise provides two sets of results. First, international trade diversion as measured by the average percentage change in bilateral international trade flows of countries 2 and 3 with the rest of the world (in %) turns out substantially smaller than the corresponding change in domestic trade flows, termed domestic trade diversion.

The estimated marginal effects of an econometric response surface a model with a rich set of interaction effects reported in Sect. 5 of the Technical "Appendix" indicate that for the larger country 2 the difference between domestic and foreign trade diversion effects increases in relative country size (measured as ratio of the endowments of country 2 over country 3). For the smaller country the opposite holds true. Moreover, for both countries in absolute terms this difference rises in the elasticity of substitution, $\sigma$, and decreases in the number of countries considered. On average international trade diversion is approximately half of the domestic trade diversion. Hence, an important part of the trade diversion effects originates from a reduction in domestic sales, while on average the diversion of international trade flows tends to be smaller. Exactly the latter is what is feared by policy makers when their trading partners, and especially neighbours, sign EIAs with other countries.

Table 5 Simulation results: domestic versus foreign trade diversion in a numerical endowment model

Second, part two of Table 5 reports the results for trade flow changes measured in percent of world expenditures. In the present setting, with 40 countries and $\sigma =6$, the initial volume of trade between countries 2 and 3 makes 4.0% of world expenditures. Their combined domestic trade amounts to 3.7%. Upon signing an EIA the trade creation is measured as 2.3 percentage points of world expenditures. The trade diverting effect is of the same magnitude. International trade diversion decreases trade of countries 2 and 3 with all third countries by 1.8 percentage points, while their combined domestic trade is reduced by 1.1 percentage points. Also in absolute terms a substantial part of trade diversion falls on domestic trade, although its relative magnitude decreases with the number of countries included. Overall, the relative size of domestic and foreign trade distortion effects remains an empirical question, however.

Based on the econometric estimates of Table 4, the trade diverting effects of EIAs referring to domestic trade are analysed for two groups of countries, one with the number of EIAs below the median and one above the median. International trade diversion comprises trade flows that are not covered by EIAs, but one of the trading partners holds at least one EIA with another trading partner. Lastly, welfare effects are measured according to Arkolakis et al. (2012) as $\left( s_{iit}^{c}/s_{iit}\right) ^{\frac{1}{ 1-\sigma }}$ and are averaged over country groups. These estimates assume an elasticity of substitution of 6.982, the preferred estimate in Bergstrand et al. (2013). Throughout, the counterfactual predictions refer to the full general equilibrium with production and expenditures adjust endogenously as a response to changes of the outward resistance term (see the Technical "Appendix" in Oberhofer and Pfaffermayr 2020 for details).

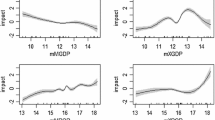
The results of the predictions of three comparative static experiments for the year 2012 are reported in Tables 6 and 7. Figure 1 illustrates their time path. The first counterfactual scenario looks at the impact if EIAs put in force between between 1994 and 2012, setting the EIA-dummy and all its lags to zero for all country pairs. Hence, the difference between the predicted actual trade flows and the counterfactual ones identifies the impact of these new EIAs. The trade creation effects, averaged over all EIA-members, are estimated as $21.3\,[12.2, 30.3]$ percent.¹¹ There is pronounced trade creation as one would expect and as is found in the literature. As a consequence, countries with many EIAs in force witnessed a welfare increase of $2.8\,[1.3, 4.3]$ percent, while countries with participating in a small number EIAs gained $1.0\,[0.3, 1.6]$ percent.

However, there are substantial trade diversion effects as well. The EIAs have reduced domestic trade by $-15.1\,[-22.4,-7.9]$ percent for those countries with many EIAs in force and by $-5.5\,[-8.9,-2.0]$ percent for countries holding just a few. International trade diversion is predicted as $-8.5\,[-13.1,-3.9]$ percent in 2012. Similar to the simulations above, a substantial part of the trade diversion effects comes from a reduction of domestic sales, dominating international trade diversion. The average difference between domestic and international trade diversion is estimated as $-1.7\,[-2.4,-1.0]$ percentage points and it is significantly different from zero.¹²

While trade creation effects of EIAs are comparable to the literature, the estimated size of the trade diversion effects is higher than that in other contributions, e.g. Bergstrand et al. (2015). As shown in Fig. 1, both the estimated trade creation and trade diversion effects of EIAs moderately increased in absolute value over time, reflecting the growing number of EIAs on the one hand, and phasing-in effects on the other hand.

In addition, Table 6 reports $95\%$-confidence intervals based on 2000 parametric bootstraps. For both the constrained and the unconstrained PPML estimations the bootstrap standard errors are higher than the delta method-standard errors in case of trade creation and lower in case of trade diversion. This finding is in line with the Monte Carlo simulations. The approximation of the standard errors by the delta method is especially weak if they are high (relative to the point estimate), here in case of domestic trade diversion of countries with few EIAs in place.

For comparison Table 6 displays the estimated counterfactual effects using the unconstrained PPML parameter estimates. Note the baseline scenario is solved in an extra step and does not use the out-of-sample predictions of the constrained PPML estimates. As the estimated parameters turn out lower in absolute value (see Table 4), so do the counterfactual predictions. The largest difference is found for average trade creation effect, which is estimated as $17.6\,[9.7,25.5]$ percent as compared to $21.5\,[12.2, 30.3]$ percent implied by the constrained PPML estimator. The estimated standard errors based on the unconstrained PPML estimates and the delta method turn out lower than that of the constrained PPML estimates on average ($-9.4$%). Bootstrapping mitigates this effect ($-6.1$%). An exception form the estimated trade diversion effects with the delta method-standard error being lower by 12.5% and the bootstrap standard errors by 13.0%.

Putting the estimated EIA-effects into perspective, the second set of experiments assesses the impact of multilateral versus preferential trade liberalization efforts. This scenario sets the EIA-dummy and all its lags counterfactually 1 for all country pairs. So it calculates the effects on trade and welfare that would have been observed if all countries had participated in an EIA and trade barriers had been reduced multilaterally by 37%.

In this scenario trade flows that are not covered by an EIA in 2012 would increase by $23.8\,[16.6,31.0]$ percent, while trade flows covered by EIAs would only marginally decrease by $-2.0\, [-5.6,1.4]$ percent on average, which is insignificant. The involved welfare effects point to an average increase of $1.9\, [0.7,3.1]$ percent for countries with few EIAs and to one of $0.8\, [0.1,1.5]$ percent for those countries with many EIAs in force. Hence, it seems that the currently observed spaghetti bowl induced by EIAs does not exhaust the possible welfare gains of a multilateral trade liberalization. In this scenario the estimated delta method based standard errors are much weaker approximations as the estimated effects are not as precisely estimated as the counterfactual effects in the other scenarios.

The third counterfactual scenario additionally sets all border related variables to zero so that trade flows are counterfactually restricted to their 1994-level with all trade barriers absorbed by the country-pair fixed effects. This experiment

Table 6 Trade creation and trade diversion effects of EIAs, counterfactual predictions for 2012

Table 7 Welfare effects of EIAs, counterfactual predictions for 2012

allows to compare the impact of the EIAs formed between 1994 and 2012 to the increase in trade resulting from the secular globalization trends. Compared to the 1994-benchmark the group of EIA- member countries enhanced bilateral trade by $93.6\,[77.2,110.1]$ percent between 1994 and 2012, i.e., by more than twice as new EIAs did. In comparison, trade flows not covered by an EIA increased by $43.4\,[31.3,55.4]$ percent. Hence, trade diverting effects of EIAs are still visible and substantial even if the reduction of border effects are taken into account. Overall, secular globalization trends seem to be much stronger and more dynamic in expanding international trade as compared to the efforts of economic policy. Countries with many EIAs in force experienced a much higher decrease in domestic trade as a response to the establishment of EIAs ($-37.2\,[-43.2,-31.2]$ percent) as compared to those with a few in force ($-23.7\,[-27.4,-20.0]$ percent). As a result these countries had been able to reap higher welfare gains ($8.5\,[6.6,10.3]$ vs.

Fig. 1

Counterfactual predictions of Scenarios 1–3

($4.9\,[4.0,5.8]$ percent).

Figure 1 displays the results of Scenarios 1–3 graphically for the period 1997–2012.¹³ Interestingly, the figure shows that trade creation and diversion effects changed only very moderately over time. In contrast, the reduction of border effects in course of the secular globalization trend show a much more pronounced increase in bilateral trade flows over this period. The graph also illustrates that domestic trade diversion effects tend to be larger than that of international trade diversion in all periods.

While the trade creating and trade diverting effects of EIAs as well as their welfare effects are significant in almost all cases, there is substantial uncertainty induced by parameter estimation. Despite rather precisely estimated direct EIA effects, the counterfactual predictions, especially the estimated welfare effects of EIAs, exhibit quite large confidence intervals. This issue seems to be overlooked in many applications that evaluate the impact of EIAs. A detailed comparison of the delta method and a parametric bootstrapping procedure for calculating the standard error of counterfactual changes indicates that the computational efficiency of the delta method comes at the cost of approximation errors, especially if parameters are not estimated with high precision.

5 Conclusions

PPML estimation of gravity models of international trade potentially involves a huge set of dummies in a high dimensional panel. Even if one wipes out country-pair fixed effects and uses zig–zag algorithms to handle country-pair, exporter-time and importer-time fixed effects to obtain consistently estimated structural trade cost parameters, econometric issues remain. Proper inference for parameter estimates and counterfactual predictions needs unbiased parameter estimates but also robust and unbiased estimates of the standard errors.

The present contribution uses a constrained panel PPML estimator, which exploits the restrictions imposed by the system of multilateral resistances for both estimation and counterfactual predictions. In this setting all dummies, including the country-pair fixed effects, are functionally determined by the structural trade cost parameters and the countries’ gross production and expenditures. This estimation procedure avoids the bias of the structural trade cost parameter estimates induced by the estimation of the large number of dummies and the estimated robust standard errors reveal only small bias. In the Monte Carlo simulations the delta method delivers reliable standard errors of the predicted counterfactual changes as well as the welfare effects. It thus may serve as an alternative to computationally intensive bootstrapping procedures. The results of the empirical analysis are less favourable in this respect, however.

Applying the constrained panel PPML estimator to a panel of bilateral trade relationships of 65 countries over the period 1994–2012 illustrates the usefulness of this estimation procedure. Estimates indicate a secular trend in globalization that induced a pronounced deterioration of border effects. At the same time many EIAs came into force that led to pronounced trade creation effects. The cost is international trade diversion elsewhere. The estimated trade diversion effects induced by the adjustment of multilateral resistances turn out significant and substantial. However, most of the trade diversion effects are coming from a reduction in domestic sales, while the diversion of international trade is small. Actually, this issue is of concern of policy makers when their trading partners sign EIAs with other countries.

However, the spaghetti bowl of EIA relationships by far does not exhaust the potential welfare gains of multilateral trade liberalization. A multilateral trade liberalization effort would remove the trade diverting effects of EIAs and induce sizeable positive welfare effects, especially for those countries with just a few EIAs in force. At the same time, international trade flows between country pairs that actually have EIAs in force would only marginally be reduced. However, the confidence intervals of the estimated counterfactual changes are quite large, an issue that seems to be overlooked in the literature.

Appendix to trade creation and trade diversion of economic integration agreements revisited: a constrained panel pseudo-maximum likelihood approach

1.1 Constrained PPML-estimation in three-way panels

The following notation is used. Let C denote the number of countries which are observed over T periods. Trade flows are stacked in the $C^{2}T\times 1$ vector s and the K explanatory variables with variation over country pairs and time in Z with corresponding structural slope parameters $\alpha$. $\mu _{ij}$ are the country-pair fixed effects. $\beta _{it}(\alpha ,\mu )$ and $\gamma _{jt}(\alpha ,\mu )$ denote the normalized multilateral resistance terms. Lastly, $\eta _{ijt}$ stands for independent, possibly heteroskedastic disturbances with $E[\eta _{ijt}|Z,V]=1$, where V is a diagonal matrix with typical element $v_{ijt}$, which takes the value 1 if the trade flow for ijt is observed and zero else. Missingness has to occur at random to obtain consistent estimators.

The structural gravity model is defined in Eqs. (1)–(3) in text and reads

$$\begin{aligned} s_{ijt}=\, & {} e^{z_{ijt}^{\prime }\alpha +\beta _{it}(\alpha ,\mu )+\gamma _{jt}(\alpha ,\mu )+\mu _{ij}}\eta _{ijt}. \\ \kappa _{it}= & {} \sum _{j=1}^{C}e^{z_{ijt}^{\prime }\alpha +\beta _{it}(\alpha ,\mu )+\gamma _{jt}(\alpha ,\mu )+\mu _{ij}},\quad i=1,\ldots,C-1 \\ \theta _{jt}= & {} \sum _{i=1}^{C}e^{z_{ijt}^{\prime }\alpha +\beta _{it}(\alpha ,\mu )+\gamma _{jt}(\alpha ,\mu )+\mu _{ij}},\quad j=1,\ldots,C \end{aligned}$$

In matrix form with additive disturbances $\varepsilon$ one thus obtains

$$\begin{aligned} s=\, & {} m(\vartheta )+\varepsilon \\ \theta=\, & {} D'm(\vartheta ), \end{aligned}$$

where $\vartheta =[\alpha ^{\prime },\beta ^{\prime }, \gamma ^{\prime }, \mu ^{\prime }]^{\prime }$ is the full parameter vector, $m(\vartheta )$ has typical element $e^{z_{ijt}^{\prime }\alpha +\beta _{it}(\alpha ,\mu )+\gamma _{jt}(\alpha ,\mu )+\mu _{ij}}$ and the typical element of $\varepsilon$ is $m_{ijt}(\vartheta )(\eta _{ijt}-1)$.

The $C^{2}T\times (C-1)^{2}$ design matrix $D_{\mu }$ refers to country-pair dummies and $D_{\phi }$ denotes the $C^{2}T\times \left( 2C-1\right) T$ design matrix for the exporter-time and importer-time dummies. Further, $D=[D_\phi , VD_\mu ]$, $W=[Z,D]$, $W_\phi =[Z,D_\phi ]$. Lastly, we define the $\left( 2C-1\right) T\times 1$ vector $\theta _{\phi }$ =($\kappa _{11},...,\kappa _{C-1,T},\theta _{11},..,\theta _{CT})^{\prime }$ of gross production shares $\kappa _{it}$ and expenditure shares $\theta _{jt}$. The country-pair specific trade flow averages are collected in $\theta _{\mu }$, a $(C-1)^{2}\times 1$ vector with typical element $\theta _{\mu _{ij}}=\frac{1}{T}\sum _ {t=1}^Ts_{ijt}$, so that $\theta =[\theta _{\mu }^\prime , \theta _{\phi }^\prime ]^\prime$.

1.1.1 The conditional likelihood and the score

Following Palmgren (1981) and Hausman et al. (1984) one can condition on $\theta _{\mu }=D_{\mu }^{\prime }Vs$, i.e, imposing $D_{\mu }^{\prime }Vm(\vartheta )-\theta _{\mu }=0,$ $\theta _{\mu }$ being given (see Wooldridge 1999, p. 83). Since for Poisson models the conditional likelihood equals the concentrated likelihood it is useful to concentrate out the $\mu _{ij}$s to illustrate its relation to the constrained estimator, which is based on the unconditional likelihood. For this we define $m_{ijt,\phi }(\phi )=e^{w_{ijt,\phi }^{\prime }\phi }$ with $\phi =[\alpha ^{\prime },$ $\beta ^{\prime },$ $\gamma ^{\prime }]^{\prime }$ and $\theta ^\prime =[\theta _{\mu }^\prime ,\theta _{\phi }^\prime ]^\prime$. $\mu (\phi )$ is implicitly defined by the first order condition

$$\begin{aligned} D_{\mu }^{\prime }Vm(\phi ,\mu (\phi ))-\theta _{\mu }=0\text { or }e^{\mu _{ij}(\phi )}=\frac{\theta _{\mu ,ij}}{\sum _{t}v_{ijt}m_{\phi ,ijt}(\phi )}. \end{aligned}$$

(11)

Plugging in $e^{\mu _{ij}(\phi )}$ yields the constrained conditional or concentrated likelihood (with superscript C):

$$\begin{aligned}&\ln L^{C}(\phi |s,V,\theta ) \\&\quad =\sum _{i}\sum _{j}\sum _{t}(v_{ijt}s_{ijt}\ln \left( m_{\phi ,ijt}(\phi )e^{\mu _{ij}(\phi )}\right) -m_{\phi ,ijt}(\phi )e^{\mu _{ij}(\phi )})-\lambda _{\phi }^{\prime }\left( D_{\phi }^{\prime }m(\phi )-\theta _{\phi }\right) , \end{aligned}$$

where $\lambda _{\phi }$ denotes the vector of Lagrange multipliers referring to the restrictions imposed by the system of multilateral resistances. Observe that $\vartheta =[\phi ^{\prime },\mu (\phi )^{\prime }]^{\prime }$. Applying the implicit function theorem to (1) yields

$$\begin{aligned} \tfrac{\partial \mu (\phi )}{\partial \phi ^{\prime }}=-\left( D_{\mu }^{\prime }VM(\vartheta )D_{\mu }\right) ^{-1}D_{\mu }^{\prime }VM(\vartheta )W_{\phi }, \end{aligned}$$

assuming that $D_{\mu }^{\prime }VM({\vartheta })D_{\mu }$ is invertible. The score of the constrained conditional likelihood with respect to $\phi$ can then be written as

$$\begin{aligned} \tfrac{\partial \ln L^{C}(\phi |s,V,\theta )}{ \partial \phi }=\, & {} \sum _{i}\sum _{j}\sum _{t}v_{ijt}\left( s_{ijt}-m_{ijt}(\phi ,\mu _{ij}(\phi )\right) \left( w_{\phi ,ijt}+\tfrac{ \partial \mu _{ij}(\phi )}{\partial \phi ^{\prime }}\right) \\&+\left( W_{\phi }+D_{\mu }\tfrac{\partial \mu (\phi )}{\partial \phi ^{\prime }}\right) ^{\prime }M(\vartheta )D_{\phi }\lambda _{\phi } \\=\, & {} W_{\phi }^{\prime }\underset{Q_{\mu }(\vartheta )}{\underbrace{\left( I_{TC^{2}}-M(\vartheta )VD_{\mu }\left( D_{\mu }^{\prime }VM(\vartheta )D_{\mu }\right) ^{-1}D_{\mu }^{\prime }\right) }} \\&*\left( V(s-m(\vartheta ))+M(\vartheta )D_{\phi }\lambda _{\phi }\right) . \end{aligned}$$

$Q_{\mu }(\vartheta )$ is a projection matrix the removes country pair effects. Since $Vm(\vartheta )=M(\vartheta )VD_{\mu }\iota _{(C-1)^{2}}$ it follows that

$$\begin{aligned} W_{\phi }^{\prime }Q_{\mu }(\vartheta )Vm(\vartheta )=\, & {} W_{\phi }^{\prime }\left( I_{TC^{2}}-M(\vartheta )VD_{\mu }\left( D_{\mu }^{\prime }VM(\vartheta )D_{\mu }\right) ^{-1}D_{\mu }^{\prime }\right) M(\vartheta )VD_{\mu }\iota _{(C-1)^{2}} \\=\, & {} W_{\phi }^{\prime }\left( VM(\vartheta )D_{\mu }\iota _{(C-1)^{2}}-M(\vartheta )VD_{\mu }\iota _{(C-1)^{2}}\right) =0. \end{aligned}$$

The score of the constrained conditional likelihood solved at $\widehat{ \vartheta }=[{\widehat{\phi }}^{\prime },\mu ({\widehat{\phi }})^{\prime }]^{\prime }$ can thus be written as

$$\begin{aligned} \tfrac{\partial \ln L^{C}(\phi |s,V,\theta )}{ \partial \phi }=\, & {} W_{\phi }^{\prime }Q_{\mu }({\widehat{\vartheta }} )Vs+W_{\phi }^{\prime }Q_{\mu }({\widehat{\vartheta }})M({\widehat{\vartheta }} )D_{\phi }\lambda _{\phi }=0 \\ \tfrac{\partial \ln L^{C}(\phi |s,V,\theta )}{ \partial \lambda }=\, & {} D_{\phi }m(\vartheta )-\theta _{\mu }. \end{aligned}$$

The score of the Lagrangian of the constrained unconditional likelihood given as

$$\begin{aligned} \tfrac{\partial \ln L(\vartheta |s,V,\theta )}{\partial \phi }=\, & {} W_{\phi }^{\prime }V(s-m(\vartheta ))+W_{\phi }^{\prime }M(\vartheta )VD_{\mu }\lambda _{\mu }+W_{\phi }^{\prime }M(\vartheta )D_{\phi }\lambda _{\phi } \\ \tfrac{\partial \ln L(\vartheta |s,V,\theta )}{\partial \mu }=\, & {} D_{\mu }^{\prime }V(s-m(\vartheta ))+D_{\mu }^{\prime }M(\vartheta )VD_{\mu }\lambda _{\mu }+D_{\mu }^{\prime }M(\vartheta )D_{\phi }\lambda _{\phi } \\ \tfrac{\partial \ln L(\vartheta |s,V,\theta )}{\partial \lambda _{\mu }}= \,& {} \theta _{\mu }-D_{\mu }^{\prime }Vm(\vartheta ) \\ \tfrac{\partial \ln L(\vartheta |s,V,\theta )}{\partial \lambda _{\phi }}=\, & {} \theta _{\phi }-D_{\phi }^{\prime }m(\vartheta ) \end{aligned}$$

Setting $\left. \frac{\partial \partial \ln L(\vartheta |s,V,\theta )}{ \partial \mu }\right| _{\vartheta ={\widehat{\vartheta }}}=0$ yields

$$\begin{aligned} {\widehat{\lambda }}_{\mu }=\, & {} -\left( D_{\mu }^{\prime }M({\widehat{\vartheta }} )VD_{\mu }\right) ^{-1}D_{\mu }^{\prime }M({\widehat{\vartheta }})D_{\phi }\lambda _{\phi }-\left( D_{\mu }^{\prime }M({\widehat{\vartheta }})VD_{\mu }\right) \underset{\theta _{\mu }-D_{\mu }^{\prime }Vm({\widehat{\vartheta }} )=0}{^{-1}\underbrace{D_{\mu }^{\prime }V(s-m({\widehat{\vartheta }}))}} \\=\, & {} -\left( D_{\mu }^{\prime }M({\widehat{\vartheta }})VD_{\mu }\right) ^{-1}D_{\mu }^{\prime }M({\widehat{\vartheta }})D_{\phi }{\widehat{\lambda }} _{\phi }. \end{aligned}$$

Inserting ${\widehat{\lambda }}_{\mu }$ in the score and setting the remaining score equations equal to zero leads to

$$\begin{aligned} 0=\, & {} W_{\phi }^{\prime }V(s-m({\widehat{\vartheta }}))+W_{\phi }^{\prime }\left( I_{TC^{2}}-M({\widehat{\vartheta }})VD_{\mu }\left( D_{\mu }^{\prime }VM({\widehat{\vartheta }})D_{\mu }\right) ^{-1}D_{\mu }^{\prime }\right) M( {\widehat{\vartheta }})D_{\phi }{\widehat{\lambda }}_{\phi } \\=\, & {} W_{\phi }^{\prime }V(s-m({\widehat{\vartheta }}))+W_{\phi }^{\prime }Q_{\mu }({\widehat{\vartheta }})M({\widehat{\vartheta }})D_{\phi }{\widehat{\lambda }} _{\phi }, \end{aligned}$$

while the score for the $\mu$ becomes redundant whenever $D_{\mu }^{\prime }V(s-m({\widehat{\vartheta }}))=0.$ Next observe that

$$\begin{aligned} m({\widehat{\vartheta }})=\, & {} M_{\phi }({\widehat{\phi }})D_{\mu }\underset{ {\widehat{\pi }}}{\underbrace{(D_{\mu }^{\prime }VM_{\phi }(\widehat{\vartheta })D_{\mu })^{-1}D_{\mu }^{\prime }Vs}} \\=\, & {} M({\widehat{\phi }})D_{\mu }(D_{\mu }^{\prime }VM({\widehat{\vartheta }} )D_{\mu })^{-1}D_{\mu }^{\prime }Vs, \end{aligned}$$

where ${\widehat{\pi }}$ has typical element $\exp ({\widehat{\mu }}_{ij})$ and $M_{\phi }({\widehat{\phi }})$ is a diagonal matrix with typical element $e^{w_{ijt,\phi }^{\prime }{\widehat{\phi }}}.$ Note $(D_{\mu }^{\prime }VM_{\phi }({\widehat{\vartheta }})D_{\mu })^{-1}$ is a diagonal matrix with typical diagonal element $\frac{1}{\sum _{t}v_{ijt}m_{\phi ,ijt}(\phi )}$ and zero off-diagonal elements. Hence, it follows that

$$\begin{aligned} W_{\phi }^{\prime }V\left( s-m({\widehat{\vartheta }})\right) =W_{\phi }^{\prime }V\left( I_{TC^{2}}-M({\widehat{\vartheta }})D_{\mu }(D_{\mu }^{\prime }VM({\widehat{\vartheta }})D_{\mu })^{-1}D_{\mu }^{\prime }V\right) s=W_{\phi }^{\prime }Q_{\mu }({\widehat{\vartheta }})Vs. \end{aligned}$$

The score equations of constrained unconditional likelihood can be written as

$$\begin{aligned} 0=\, & {} W_{\phi }^{\prime }Q_{\mu }({\widehat{\vartheta }})Vs-W_{\phi }^{\prime }Q_{\mu }({\widehat{\vartheta }})M({\widehat{\vartheta }})D_{\phi }\widehat{ \lambda }_{\phi } \\ 0=\, & {} \theta _{\phi }-D_{\phi }^{\prime }m({\widehat{\vartheta }}), \end{aligned}$$

which is equivalent to the score of the constrained conditional Poisson likelihood.

1.1.2 Iterative estimation of the constrained panel PPML model

Remember ${\widehat{M}}=diag(m_{ijt}({\widehat{\vartheta }})),$ ${\widehat{\pi }} =\exp ({\widehat{\mu }}_{ij})$, ${\widehat{M}}_{\pi }=diag({\widehat{\pi }} _{11},\ldots,{\widehat{\pi }}_{C-1,C-1}),$ $m_{\phi ,ijt}({\widehat{\phi }})$ $=e^{z_{ijt}^{\prime }{\widehat{\alpha }}+\beta _{it}({\widehat{\alpha }}, {\widehat{\mu }})+\gamma _{jt}({\widehat{\alpha }},{\widehat{\mu }})}$ and ${\widehat{\pi }}=(D_{\mu }^{\prime }VM_{\phi }({\widehat{\vartheta }})D_{\mu })^{-1}\theta _{\mu }.$ Following Falocci et al. (2009) and Pfaffermayr (2020) iteration step $r+1$ uses the linearization of the score around ${\hat{\vartheta }}_{r}.$ The involved remainder terms are denoted by $a_{r}$, $b_{r}$ and $c_{r}$, respectively. Further, the following matrices are used to abbreviate notation. For simplicity their arguments are skipped.

$$\begin{aligned} {\widehat{Q}}_{\mu ,r}=\; & {} I-{\widehat{M}}_{r}VD_{\mu }\left( D_{\mu }^{\prime }V {\widehat{M}}_{r}D_{\mu }\right) ^{-1}D_{\mu }^{\prime } \\ {\widehat{G}}_{r}=\; & {} W_{\phi }^{\prime }{\widehat{Q}}_{\mu ,r}V{\widehat{M}} _{r}W_{\phi } \\ {\widehat{F}}_{r}^{\prime }=\; & {} W_{\phi }^{\prime }{\widehat{Q}}_{\mu ,r}\widehat{ M}_{r}D_{\phi }. \end{aligned}$$

(i) Expanding the restriction referring to ${\widehat{\mu }}$:

$$\begin{aligned} \underset{0}{\underbrace{D_{\mu }^{\prime }Vm({\widehat{\vartheta }} _{r+1})-\theta _{\mu }}}=\, & {} \underset{0}{\underbrace{D_{\mu }^{\prime }Vm(\vartheta _{r})-\theta _{\mu }}}+D_{\mu }^{\prime }V{\widehat{M}} _{r}W_{\phi }\left( {\widehat{\phi }}_{r+1}-{\widehat{\phi }}_{r}\right) \\&+D_{\mu }^{\prime }V{\widehat{M}}_{r}D_{\mu }\left( {\widehat{\mu }}_{r+1}- {\widehat{\mu }}_{r}\right) +a_{r} \\ \left( {\widehat{\mu }}_{r+1}-{\widehat{\mu }}_{r}\right)=\, & {} \left( D_{\mu }^{\prime }V{\widehat{M}}_{r}D_{\mu }\right) ^{-1}\left( D_{\mu }^{\prime }V {\widehat{M}}_{r}W_{\phi }\left( {\widehat{\phi }}_{r+1}-{\widehat{\phi }} _{r}\right) +a_{r}\right) . \end{aligned}$$

(ii) Expanding the score referring to ${\widehat{\phi }}_{r}$ : Using the expansion of $W_{\phi }^{\prime }V(s-m({\widehat{\vartheta }}_{r}))$ at the parameter values of iteration r at given ${\widehat{F}}_{r}^{\prime } {\widehat{\lambda }}_{\phi ,r}$ it follows that

$$\begin{aligned}&\underset{0}{\underbrace{W_{\phi }^{\prime }V(s-m({\widehat{\vartheta }} _{r+1}))}}\\&\quad =W_{\phi }^{\prime }V\left( s-{\widehat{m}}_{r}\right) -W_{\phi }^{\prime }V{\widehat{M}}_{r}W_{\phi }\left( {\widehat{\phi }}_{r+1}-\widehat{ \phi }_{r}\right) \\&\qquad -W_{\phi }^{\prime }V{\widehat{M}}_{r}D_{\mu }\left( {\widehat{\mu }}_{r+1}- {\widehat{\mu }}_{r}\right) +{\widehat{F}}_{r}^{\prime }{\widehat{\lambda }}_{\phi ,r}+b_{r} \\&\quad = W_{\phi }^{\prime }V\left( s-{\widehat{m}}_{r}\right) -W_{\phi }^{\prime }V {\widehat{M}}_{r}W_{\phi }\left( {\widehat{\phi }}_{r+1}-{\widehat{\phi }} _{r}\right) \\&\qquad -W_{\phi }^{\prime }V{\widehat{M}}_{r}D_{\mu }\left( D_{\mu }^{\prime }V {\widehat{M}}_{r}D_{\mu }\right) ^{-1}\left( D_{\mu }^{\prime }V{\widehat{M}} _{r}W_{\phi }\left( {\widehat{\phi }}_{r+1}-{\widehat{\phi }}_{r}\right) +a_{r}\right) +{\widehat{F}}_{r}^{\prime }{\widehat{\lambda }}_{\phi ,r}+b_{r} \\&\quad =W_{\phi }^{\prime }V\left( s-{\widehat{m}}_{r}\right) -W_{\phi }^{\prime } \left[ \underset{{\widehat{Q}}_{\mu ,r}}{\underbrace{I_{TC^{2}}-{\widehat{M}} _{r}VD_{\mu }\left( D_{\mu }^{\prime }V{\widehat{M}}_{r}D_{\mu }\right) ^{-1}D_{\mu }^{\prime }}}\right] V{\widehat{M}}_{r}W_{\phi }\left( \widehat{ \phi }_{r+1}-{\widehat{\phi }}_{r}\right) \\&\qquad +{\widehat{F}}_{r}^{\prime }{\widehat{\lambda }}_{\phi ,r}-\underset{\widetilde{ b}_{r}}{\underbrace{W_{\phi }^{\prime }V{\widehat{M}}_{r}D_{\mu }\left( D_{\mu }^{\prime }V{\widehat{M}}_{r}D_{\mu }\right) ^{-1}a_{r}+b_{r}}} \\&\quad =W_{\phi }^{\prime }V\left( s-{\widehat{m}}_{r}\right) -\underset{{\widehat{G}} _{r}}{\underbrace{W_{\phi }^{\prime }{\widehat{Q}}_{\mu ,r}V{\widehat{M}} _{r}W_{\phi }}}\left( {\widehat{\phi }}_{r+1}-{\widehat{\phi }}_{r}\right) + {\widehat{F}}_{r}^{\prime }{\widehat{\lambda }}_{\phi ,r}+{\widetilde{b}}_{r} \end{aligned}$$

or

$$\begin{aligned} {\widehat{\phi }}_{r+1}-{\widehat{\phi }}_{r}={\widehat{G}}_{r}^{-1}\left( W_{\phi }^{\prime }V\left( s-{\widehat{m}}_{r}\right) +{\widehat{F}}_{r}^{\prime }{\widehat{\lambda }}_{\phi ,r}+{\widetilde{b}}_{r}\right) . \end{aligned}$$

(iii) Expanding the restrictions implied by the system of trade resistances:

$$\begin{aligned} \underset{0}{\underbrace{D_{\phi }^{\prime }{\widehat{m}}_{r+1}-\theta _{\phi } }}=\, & {} D_{\phi }^{\prime }{\widehat{m}}_{r}-\theta _{\phi }+D_{\phi }^{\prime } {\widehat{M}}_{r}W_{\phi }\left( {\widehat{\phi }}_{r+1}-{\widehat{\phi }} _{r}\right) +D_{\phi }^{\prime }{\widehat{M}}_{r}D_{\mu }\left( {\widehat{\mu }} _{r+1}-{\widehat{\mu }}_{r}\right) +c_{r} \\ \theta _{\phi }-D_{\phi }^{\prime }{\widehat{m}}_{r}=\, & {} D_{\phi }^{\prime } {\widehat{M}}_{r}W_{\phi }\left( {\widehat{\phi }}_{r+1}-{\widehat{\phi }} _{r}\right) \\&-D_{\phi }^{\prime }{\widehat{M}}_{r}D_{\mu }\left( D_{\mu }^{\prime }V {\widehat{M}}_{r}D_{\mu }\right) ^{-1}D_{\mu }^{\prime }V{\widehat{M}} _{r}W_{\phi }\left( {\widehat{\phi }}_{r+1}-{\widehat{\phi }}_{r}\right) \\&-\underset{{\widetilde{c}}_{r}}{\underbrace{D_{\phi }^{\prime }V{\widehat{M}} _{r}D_{\mu }\left( D_{\mu }^{\prime }V{\widehat{M}}_{r}D_{\mu }\right) ^{-1}a_{r}+c_{r}}} \\=\, & {} D_{\phi }^{\prime }\left( I_{TC^{2}}-{\widehat{M}}_{r}D_{\mu }\left( D_{\mu }^{\prime }V{\widehat{M}}_{r}D_{\mu }\right) ^{-1}D_{\mu }^{\prime }V\right) {\widehat{M}}_{r}W_{\phi }\left( {\widehat{\phi }}_{r+1}-{\widehat{\phi }} _{r}\right) +{\widetilde{c}}_{r} \\=\, & {} {\widehat{F}}_{r}\left( {\widehat{\phi }}_{r+1}-{\widehat{\phi }}_{r}\right) + {\widetilde{c}}_{r}. \end{aligned}$$

(iv) Solving for ${\widehat{\lambda }}_{\phi ,r}$ using (ii) and (iii):

$$\begin{aligned} 0=\, & {} {\widehat{F}}_{r}\left( {\widehat{\phi }}_{r+1}-{\widehat{\phi }}_{r}\right) + {\widetilde{c}}_{r}-{\widehat{F}}_{r}{\widehat{G}}_{r}^{-1}\left( W_{\phi }^{\prime }V(s-{\widehat{m}}_{r})+{\widehat{F}}_{r}^{\prime }{\widehat{\lambda }} _{\phi ,r}+{\widetilde{b}}_{r}\right) \\=\, & {} {\widehat{F}}_{r}\left( {\widehat{\phi }}_{r+1}-{\widehat{\phi }}_{r}\right) + {\widetilde{c}}_{r}-{\widehat{F}}_{r}{\widehat{G}}_{r}^{-1}{\widehat{F}}_{r}^{\prime }{\widehat{\lambda }}_{\phi ,r}-{\widehat{F}}_{r}{\widehat{G}}_{r}^{-1}\left( W_{\phi }^{\prime }V(s-{\widehat{m}}_{r})+{\widetilde{b}}_{r}\right) \\ {\widehat{\lambda }}_{\phi ,r}= \,& {} \left( {\widehat{F}}_{r}{\widehat{G}}_{r}^{-1} {\widehat{F}}_{r}^{\prime }\right) ^{-1}\left[ \underset{\theta _{\phi }-D_{\phi }^{\prime }{\widehat{m}}_{r}-c_{r}}{\underbrace{{\widehat{F}} _{r}\left( {\widehat{\phi }}_{r+1}-{\widehat{\phi }}_{r}\right) }}-{\widehat{F}} _{r}{\widehat{G}}_{r}^{-1}\left( W_{\phi }^{\prime }V(s-{\widehat{m}}_{r})+ {\widetilde{b}}_{r}\right) +{\widetilde{c}}_{r}\right] \end{aligned}$$

(v) Iteration step for ${\widehat{\phi }}_{r+1}$: Inserting for ${\widehat{\lambda }}_{\phi ,r}$ in the score equation then yields

$$\begin{aligned} {\widehat{\phi }}_{r+1}-{\widehat{\phi }}_{r}=\, & {} {\widehat{G}}_{r}^{-1}W_{\phi }V\left( s-{\widehat{m}}_{r}\right) \\&+{\widehat{G}}_{r}^{-1}{\widehat{F}}_{r}^{\prime }\left( {\widehat{F}}_{r} {\widehat{G}}_{r}^{-1}{\widehat{F}}_{r}^{\prime }\right) ^{-1}\left[ {\widehat{F}} _{r}\left( {\widehat{\phi }}_{r+1}-{\widehat{\phi }}_{r}\right) \right. \\&-\left. {\widehat{F}}_{r}{\widehat{G}}_{r}^{-1}\left( W_{\phi }^{\prime }V(s- {\widehat{m}}_{r})+{\widetilde{b}}_{r}\right) +{\widetilde{c}}_{r}\right] + {\widetilde{b}}_{r} \\=\, & {} \left( {\widehat{G}}_{r}^{-1}-{\widehat{G}}_{r}^{-1}{\widehat{F}}_{r}^{\prime }\left( {\widehat{F}}_{r}{\widehat{G}}_{r}^{-1}{\widehat{F}}_{r}^{\prime }\right) ^{-1}{\widehat{F}}_{r}{\widehat{G}}_{r}^{-1}\right) W_{\phi }^{\prime }V(s- {\widehat{m}}_{r}) \\&+{\widehat{G}}_{r}^{-1}{\widehat{F}}_{r}^{\prime }\left( {\widehat{F}}_{r} {\widehat{G}}_{r}^{-1}{\widehat{F}}_{r}^{\prime }\right) ^{-1}\left( \theta _{\phi }-D_{\phi }^{\prime }{\widehat{m}}_{r}\right) +\widetilde{{\widetilde{b}}} _{r} \end{aligned}$$

(vi) Country pair effects:

Given ${\widehat{\phi }}_{r+1}$, $\widehat{ \pi }_{r+1}$ is calculated as

$$\begin{aligned} {\widehat{\pi }}_{r+1}=(D_{\mu }^{\prime }V{\widehat{M}}_{\phi ,r+1}D_{\mu })^{-1}D_{\mu }^{\prime }Vs. \end{aligned}$$

Upon convergence it holds that ${\widehat{\phi }}_{r+1}={\widehat{\phi }}_{r}$, ${\widehat{\pi }}_{r+1}={\widehat{\pi }}_{r}$ as well as $a_{r}=0,b_{r}=0$ and $c_{r}=0.$ Then it follows that $\theta _{\phi }-D_{\phi }^{\prime }\widehat{m }_{r}=0$ and $\left( {\widehat{G}}_{r}^{-1}-{\widehat{G}}_{r}^{-1}{\widehat{F}} _{r}^{\prime }\left( {\widehat{F}}_{r}{\widehat{G}}_{r}^{-1}{\widehat{F}} _{r}^{\prime }\right) ^{-1}{\widehat{F}}_{r}{\widehat{G}}_{r}^{-1}\right)$ $*W_{\phi }^{\prime }V(s-{\widehat{m}}_{r})=0$ (see Newey and McFadden 1994, p. 2219 and the projection estimator of Heyde and Morton 1993, p. 756).

1.1.3 Derivations for the asymptotic distribution of $\widehat{ \alpha }$

For the derivation of the asymptotic distribution of $\ {\widehat{\alpha }}$ the elements of $M(\vartheta ),$ $m_{ijt}(\vartheta ),$ are assumed to be uniformly bounded, i.e., $c_{a}/C^{2}<m_{ijt}(\vartheta )<(1-c_{a})/C^{2}$ for some positive constant $c_{a}$ and thus decrease at rate $C^{2}$. Further, $C^{2}\varepsilon _{ij},$ $ij=1,...,C$ is independently distributed as $(0,\sigma _{ij}^{2})$ with $0<\sigma _{ij}^{2}$ $<{\overline{\sigma }} <\infty$ and bounded support such that $m_{ij}(\vartheta _{0})+\varepsilon _{ij}>0.$ Further details on the other regularity assumptions and proofs are given in Pfaffermayr (2020).

The set of restrictions is assumed to hold at true parameters, i.e., $D^{\prime }m(\vartheta _{0})-\theta =0.$ In addition to the system of multilateral resistance equations, it holds that $\theta _{\mu }-D_{\mu }^{\prime }Vm(\vartheta _{0})=$ 0 due to the conditioning on $\theta _{\mu }.$

Defining the matrices $G=W^{\prime }VMW,$ $F^{\prime }=W^{\prime }MD$ the mean value theorem can be applied to the score of the constrained likelihood likelihood of the full model, where $G^{*}$ and $F^{*}$ are evaluated at $\vartheta ^{*}$, whose elements lie (element-wise) in between those of ${\widehat{\vartheta }}$ and $\vartheta _{0}.$ Then $\theta -D^{\prime }m(\vartheta _{0})=0$ implies that $\lambda _{0}=0$ and one obtains

$$\begin{aligned} \left[ \begin{array}{c} 0 \\ 0 \end{array} \right] =\left[ \begin{array}{c} W^{\prime }V\varepsilon +G^{*}\left( {\widehat{\vartheta }}-\vartheta _{0}\right) +F^{*\prime }{\widehat{\lambda }} \\ F^{*}\left( {\widehat{\vartheta }}-\vartheta _{0}\right) \end{array} \right] . \end{aligned}$$

Applying the formula for the partitioned inverse and defining $Q_{G^{-1/2}F^{\prime }}=I-G^{-1/2}F^{\prime }(FG^{-1}F^{\prime })FG^{-1/2}$ yields

$$\begin{aligned} \left[ \begin{array}{c} {\widehat{\vartheta }}-\vartheta _{0} \\ {\widehat{\lambda }} \end{array} \right] =\left[ \begin{array}{c} G^{*-1/2}Q_{G^{*-1/2}F^{*\prime }}G^{*-1/2}W^{\prime }V\varepsilon \\ (F^{*}G^{*-1}F^{*\prime })^{-1}F^{*}G^{*-1}W^{\prime }V\varepsilon \end{array} \right] . \end{aligned}$$

Lastly, as shown above the implicit function theorem applied to to $D^{\prime }m(\alpha ,\phi (\alpha ),\mu (\alpha ))-\theta =0$ implies

$$\begin{aligned} \left. \frac{\partial }{\partial \alpha }\left[ \begin{array}{c} \phi (\alpha ) \\ \mu (\alpha ) \end{array} \right] \right| _{\alpha =\alpha ^{*}}=-\left( D^{\prime }M^{*}D^{\prime }\right) ^{-1}D^{\prime }M^{*}Z \end{aligned}$$

and

$$\begin{aligned} G^{*}\left[ \begin{array}{c} I_{K} \\ -\left( D^{\prime }M^{*}D^{\prime }\right) ^{-1}D^{\prime }M^{*}Z \end{array} \right] \left( {\widehat{\alpha }}-\alpha _{0}\right) =G^{*1/2}Q_{G^{*-1/2}F^{*\prime }}G^{*-1/2}W^{\prime }V\varepsilon . \end{aligned}$$

Multiplying from left by $S=[I_{K\times K},0_{K\times (C-1)^{2}+(2C-1)T}]$, shows that

$$\begin{aligned}&SG^{*}\left( {\widehat{\alpha }}-\alpha _{0}\right) \\&\quad =S\left[ \begin{array}{c} Z^{\prime }VM^{*}VZ-Z^{\prime }VM^{*}VD\left( D^{\prime }M_{0}D\right) ^{-1}D^{\prime }M_{0}Z \\ D^{\prime }VM^{*}VZ-D^{\prime }VM^{*}VD\left( D^{\prime }M_{0}D\right) ^{-1}D^{\prime }M_{0}Z \end{array} \right] \left( {\widehat{\alpha }}-\alpha _{0}\right) \\&\quad =Z^{\prime }V\left( M^{*}-M^{*}D(D^{\prime }M^{*}D)^{-1}D^{\prime }M^{*}\right) Z\left( {\widehat{\alpha }}-\alpha _{0}\right) . \end{aligned}$$

and

$$\begin{aligned}&S\left( \left[ \begin{array}{cc} I_{K} &{} 0 \\ 0 &{} I_{(C-1)^{2}+(2C-1)T} \end{array} \right] -F^{*^{\prime }}\left( F^{*}G^{*-1}F^{*\prime }\right) ^{-1}F^{*}G^{*-1}\right) W^{\prime }V\varepsilon \\&\quad = Z^{\prime }\left( I_{TC^{2}}-M^{*}D\left( F^{*}G^{*-1}F^{*\prime }\right) ^{-1}F^{*}G^{*-1}W^{\prime }\right) V\varepsilon , \end{aligned}$$

since

$$\begin{aligned} SF^{*^{\prime }}=[I_{K\times K},0_{(C-1)^{2}+(2C-1)T}]\left[ \begin{array}{c} Z^{\prime } \\ D^{\prime } \end{array} \right] M^{*}D=Z^{\prime }M^{*}D. \end{aligned}$$

In the notation of Pfaffermayr (2020) one thus obtains

$$\begin{aligned} CT^{\frac{1}{2}}\left( {\widehat{\alpha }}-\alpha _{0}\right)=\, & {} \frac{1}{CT^{1/2}}B(\alpha ^{*})^{-1}A(\alpha ^{*})\varepsilon \\ A(\alpha )=\, & {} C^2TZ^{\prime }(I_{TC^{2}}-M(\alpha )D^{\prime }\left( F(\alpha )G(\alpha )^{-1}F(\alpha )^{\prime }\right) ^{-1}F(\alpha )G(\alpha )^{-1}W^{\prime })V \\ B(\alpha )=\, & {} Z^{\prime }V\left[ M(\alpha )-M(\alpha )D(D^{\prime }M(\alpha )D)^{-1}D^{\prime }M(\alpha )\right] Z. \end{aligned}$$

and the asymptotic distribution of $CT^{\frac{1}{2}}\left( {\widehat{\alpha }} -\alpha _{0}\right)$ as given in the text.

1.2 Monte Carlo simulations, truncated log-normal errors

Disturbances are generated as iid $exp(\epsilon _{ijt})$, where $\epsilon _{ijt}=.0222243\frac{\eta -{\bar{\eta }}}{s_{\eta }}$ and $\eta$ is truncated normal with support $[-\infty ,2]$ (Table 8).

Table 8 Monte Carlo simulation results: simulated standard errors and coverage rates of the estimated EIA parameter and counterfactual predictions under truncated log normal disturbances

1.3 Data base and the robustness of estimation results

The panel includes aggregate goods trade of manufacturing firms (converted from HS-codes to ISIC-Revision 4) observed over 3-year periods during 1994–2012 and is based on several data sources. OECD’s-STAN (Edition 2015) data serves as primary data source since it reports consistent figures for bilateral trade flows, total unilateral exports and imports, and gross production, however the latter three for OECD countries only. Trade flows are measured as nominal cif-values as reported by the importing country.

STAN’s data on gross production have been augmented by UNIDO’s database and CPEPII’s database (De Sousa et al. 2012) using PPML to regress gross production on the log of its counterpart in UNIDO and CEPII. These PPML estimates also include interactions of log production with country and year dummies as well as country and year dummies themselves. Overall 237 observations on gross production have been imputed from CEPII and the 245 from UNIDO. In a few cases production data turned out inconsistent with trade data (mainly because of negative domestic production) and production data from WIOD are used (CYP, BEL, EST, NLD, IRL, LUX, LTU, SVK, SVN). In this way the database could be expanded to 65 countries. The same imputation procedure has been applied to total unilateral exports and imports. Here the aggregates from the Nicita and Olarreaga serve additional data sources and 536 values for total unilateral exports and 546 for total unilateral imports had been imputed. Finally, in a few case data have been interpolated.

Production and expenditure data are corrected for trade with the rest of the world (ROW) as well as for trade imbalances. The value of total production country i at time t is given as $x_{i.t}=\sum _{j=1}^{C}x_{ijt}+x_{i,ROW,t}$ and total expenditure of country j by $x_{.jt}=\sum _{i=1}^{C}x_{ijt}+x_{ROW,j,t}$, where $x_{ijt}$ denotes the value of trade flows. The trade balance of country j is given as $d_{jt}=x_{j.t}-x_{.jt}$. Exports to ROW and imports from ROW of country i at time t have been aggregated in $x_{i,ROW,t}$ and $x_{ROW,i,t}$. Domestic trade flows are implicitly defined by

$$\begin{aligned} \kappa _{it}=\, & {} \frac{x_{i.t}-x_{i,ROW,t}}{Y_{t,W}}=s_{iit}+\sum _{j\ne i}^{C}s_{ijt} \\ \theta _{jt}=\, & {} \frac{x_{.jt}-d_{jt}-x_{ROW,j,t}}{Y_{t,W}} =s_{jjt}+\sum _{i\ne j}^{C}s_{ijt}, \end{aligned}$$

where $Y_{t,W}$ denotes overall (world) production or expenditure of the 65 countries. Note that $\sum _{i=1}^{C}d_{it}=0$ per definition and that $\sum _{i=1}^{C}\kappa _{it}=\sum _{j=1}^{C}\theta _{jt}=1$. Total unilateral exports and imports ($x_{i.t}$ and $x_{.jt}$) come from the aggregate country specific data. Based on these figures domestic trade is derived as $total production_{it}-total exports_{it}$ using the unilateral industry data. Thereby, 14 domestic trade flows have been set to missing because the sum of all trade flows over the 65 importer countries (including the domestic trade flows) and gross production deviated by more the 30 percent. Due to presence of missing trade flows and measurement errors the included trade flows do not aggregate exactly to domestic production $\kappa _{it}$ and domestic expenditures $\theta _{jt}$, however (Table 9).

ROW-figures are derived from the total trade flows of 224 countries (in HS-classification) and are calculated as $total exports_{it} -\sum _{j\ne i}^{C}s_{ijt}$ to get $\frac{x_{i,ROW,t}}{ Y_{t,W}}$ and $total imports_{jt}-tradebalance_{jt}-\sum _{i\ne j}^{C}s_{ijt}$ to obtain $\frac{x_{ROW,j,t}}{Y_{t,W}}$.

1.4 Robustness of the estimates in Table 4

Table 9 Robustness of alternative specifications of the structural gravity model

1.5 Response surface of trade diversion in a simulated numerical endowment model

The response surfaces use the data of Table 5 taking the absolute value of difference between domestic and international trade diversion (first panel of the table) and the plain differences of country 2 and 3 (second and third panel) as dependent variable. Explanatory variables are dummies for $\sigma =3$ and $\sigma =6$, the number of countries (20, 40 60), a similarity index based on the size of countries 2 and 3 as well as interactions there of. The Table reports average marginal effects (Tables 10, 11).

Table 10 Simulation results: average marginal effects of domestic versus foreign trade diversion in a numerical endowment model

1.6 Conditional equilibrium for Scenario 1

Table 11 Trade creation and trade diversion effects of EIAs, counterfactual predictions for 2012, base-no new EIAs