Un-diversifying during crises: Is it a good idea?

Abstract

High levels of correlation among financial assets and extreme losses are typical during crises. In such situations, investing in few assets might be a better choice than holding diversified portfolios. We show that constraining the sparse $\ell _q$-norm of portfolio weights automatically controls diversification and selects portfolios with a small number of active weights and low risk, in presence of high correlation and volatility. We highlight the diversification relationships between the minimum variance portfolio, risk budgeting strategies and diversification-constrained portfolios. Finally, we show empirically that the $\ell _q$-strategy can successfully cope with bear markets by shrinking portfolio weights and total amount of shorting.

Appendices

Appendix A: Risk decomposition

In risk management, it is important to quantify the contribution of each asset to the overall portfolio risk. One common indicator is given by the sensitivity of portfolio risk to a small change in asset allocation. In this section, we derive this measure for the portfolio standard deviation and Expected Shortfall.

Let $\varvec{w}$ be the $n \times 1$ vector of portfolio weights and $\varvec{\varSigma }$ be the $n \times n$ covariance matrix of n asset returns. The risk of the portfolio, typically measured by the standard deviation of portfolio returns $\sigma _p$, can then be expressed as follows:

$$\begin{aligned} \sigma _p = \sqrt{\varvec{w}'\varSigma \varvec{w}}. \end{aligned}$$

In order to measure the contribution of each asset to the overall portfolio risk, we can compute the Marginal Risk Contribution of asset i as the partial derivative of $\sigma _p$ with respect to $w_i$

$$\begin{aligned} { MRC}_i=\frac{\partial \sigma _p}{\partial w_i} = \frac{\sum _{j=1}^{n}\sigma _{ij}w_j}{\sigma _p}. \end{aligned}$$

${ MRC}_i$ can be also expressed as a function of $(\varvec{\varSigma } \varvec{w})$, the product of the covariance matrix and the weights vector, as follows:

$$\begin{aligned} { MRC}_i=\frac{(\varSigma w)_i}{\sigma _p} \end{aligned}$$

where $(\varSigma w)_i = \sum _{j=1}^{n}\sigma _{ij}w_j$ represents the i-th component of the column vector $(\varvec{\varSigma } \varvec{w})$. The risk contribution of asset i is then defined as the weighted ${ MRC}_i$ and represents the share of portfolio risk corresponding to the i-asset:

$$\begin{aligned} RC_i&= w_i { MRC}_i = \frac{w_i(\varSigma w)_i}{\sigma _p}\\ \sum _{i=1}^{n} RC_i&= \sum _{i=1}^{n} \frac{w_i(\varSigma w)_i}{\sigma _p} = \frac{\varvec{w}'\varSigma \varvec{w}}{\sigma _p} = \sqrt{\varvec{w}'\varSigma \varvec{w}} \end{aligned}$$

The sum of all $RC_i$ is the total portfolio risk, quantified by the standard deviation of the portfolio returns. The relative risk contribution of asset i is defined as

$$\begin{aligned} { RRC}_i=\frac{RC_i}{\sigma _p} = \frac{w_i (\varSigma w)_i}{\sigma _p^2}=\frac{w_i (\varSigma w)_i}{\varvec{w}'\varSigma \varvec{w}} \end{aligned}$$

By construction, the risk-parity portfolio has a RC$_i=\sigma _p/n$, which implies an RRC$_i= 1/n$.

From a risk budgeting perspective, it may be useful to know the composition of a portfolio also in terms of extreme risk. Let us denote by $\mu _i$ the expected return on asset i (with $i = 1, \dots , n$) and by $\mu _p$ the expected return on the portfolio obtained as the weighted sum of its constituents’ expected returns:

$$\begin{aligned} \mu _p = \sum _{i=1}^n w_i\mu _i . \end{aligned}$$

Given a constant $0 \le \alpha \le 1$, we define the Value-at-Risk of a portfolio, ${ VaR}_{p,\alpha }$, as the maximum expected loss of the portfolio at a $\alpha \%$ confidence level. We measure the extreme risk of a portfolio by the Expected Shortfall $ES_{p,\alpha }$, which represents the expected return of the portfolio in the worst $(1-\alpha )\%$ of cases. $ES_{p,\alpha }$ can be written equivalently as the expected loss of the portfolio conditional on this loss being greater than $C={ VaR}_{p,\alpha }$:

$$\begin{aligned} ES_{p,\alpha } = \mathbb {E}(\mu _p|\mu _p<C) = \mathbb {E}\left( \sum _{i=1}^n w_i\mu _i|\mu _p<C\right) . \end{aligned}$$

To compute the contribution of each asset to the overall portfolio $ES_{p,\alpha }$, we first calculate the Marginal Expected Shortfall of asset i as the partial derivative of $ES_{p,\alpha }$ with respect to $w_i$:

$$\begin{aligned} { MES}_{i,\alpha }=\frac{\partial ES_{p,\alpha }}{\partial w_i} = \mathbb {E}(\mu _i|\mu _p<C) . \end{aligned}$$

${ MES}_{i,\alpha }$ represents the increase in portfolio extreme risk caused by a marginal increase in the weight on asset i. As suggested by Benoit et al. (2013), the extreme risk contribution of each asset ${ CES}_{i,\alpha }$ can be then defined as the weighted ${ MES}_{i,\alpha }$ and indicates the share of $ES_{p,\alpha }$ due to the i-asset:

$$\begin{aligned} { CES}_{i,\alpha }&= w_i { MES}_{i,\alpha } \\ \sum _{i=1}^{n} { CES}_{i,\alpha }&= \sum _{i=1}^{n}w_i { MES}_{i,\alpha } = ES_{p,\alpha } . \end{aligned}$$

The sum of all the Contributions to Expected Shortfall ${ CES}_{i,\alpha }$ is the total portfolio Expected Shortfall.

Appendix B: $\ell _q$ properties

Let’s consider the risk minimization problem

$$\begin{aligned} \min _{\varvec{w}}&\varvec{w}'\varvec{\varSigma } \varvec{w}\nonumber \\&\mathbf{1'}{\varvec{w}} = 1 \nonumber \\&\Vert \varvec{w}\Vert _q^q\ \le c^q \end{aligned}$$

(B-1)

where $0 < q \le 1$ and $c^q>0$ is the threshold of the $\ell _{q}$-norm. This optimization could be solved as the following penalized problem (although convergence to the global optimum is not guaranteed as the $\ell _q$-penalty is non-convex).

$$\begin{aligned} \min _{\varvec{w}}&\varvec{w}'\varvec{\varSigma } \varvec{w}+\lambda \Vert \varvec{w}\Vert _q^q\nonumber \\&\mathbf{1'}{\varvec{w}} = 1 \end{aligned}$$

(B-2)

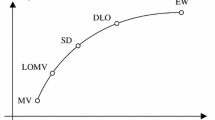
with $\lambda >0$ as a scalar controlling the intensity of the penalty. If $c\rightarrow n^{1-q}$, then the solution to problem (B-1) converges to the EW portfolio, while if $c\rightarrow 1$, it converges to the most concentrated portfolio with just one active weight, as $q\rightarrow 0^+$.

Proof

Proposition 1. Let the amount of shorting of a portfolio $\varvec{w}$ be the sum of the absolute value of its negative weights

$$\begin{aligned} S = \sum _{j=\{i:i=1,\dots n|w_i<0\}} |w_j| . \end{aligned}$$

Due to the budget constraint, the amount of null and long positions can then be written as

$$\begin{aligned} L = \sum _{j=\{i:i=1,\dots n|w_i\ge 0\}} |w_j| = S + 1 . \end{aligned}$$

Since $\Vert \varvec{w}\Vert _1 = S+L$, we also have that $\Vert \varvec{w}\Vert _1 = 2S +1$. Therefore, adding the $\ell _1$-norm to the objective function constrains the level of shorting of the portfolio. The $\ell _q$-norm represents a stricter constraint on shorting, as, for any value of q, we have

$$\begin{aligned} \Vert \varvec{w}\Vert _q^q = \sum _{i=1}^n |w_i|^q \ge \left( \sum _{i=1}^n |w_i| \right) ^q , \end{aligned}$$

and, given that $\left( \sum _{i=1}^n |w_i| \right) = 2S+1$,

$$\begin{aligned} \Vert \varvec{w}\Vert _q^q&\ge (2S+1)^q . \end{aligned}$$

Furthermore, as $0 \le q < 1$ and $(2S+1)\ge 1$, it follows that $2S+1\ge (2S+1)^q$. Thus, constraining the $\ell _q$-norm of portfolio weights, i.e., $\Vert \varvec{w}\Vert _q^q \le c$, imposes a stronger bound on the amount of shorting than the one applied by constraining the $\ell _1$-norm, i.e., $\Vert \varvec{w}\Vert _1 \le c^q$. $\square$

Proof

Proposition 2. To prove that the $\ell _{q}$-norm, with $0 < q \le 1$, is bounded by 1 and $n^{1-q}$ under the no-short-selling and budget constraints, i.e., $0 \le w_i \le 1$, $\sum _{i=1}^{n} w_1 =1$, we compute its extreme values corresponding to the most concentrated (i.e., totally invested in one asset) and the EW portfolios. Let us assume that the absolute values of the weights are sorted in descending order, from the largest to the smallest such that $|w_{(1)}| \ge |w_{(2)}| \ge \dots |w_{(n)}|$. Then, let $w_{(1)}$ be equal to 1 and therefore $w_{(j)}=0$, $j=2,\dots n$. It follows that for the most concentrated portfolio

$$\begin{aligned} \ell _{q} = \Vert \varvec{w}\Vert _q^q = \sum _{i=1}^{n} |w_i|^q = 1^q = 1 . \end{aligned}$$

The other limit case is for the EW portfolio, when $w_1=w_2=\dots =w_n=1/n$. Then,

$$\begin{aligned} \ell _{q} = \Vert \varvec{w}\Vert _q^q = \sum _{i=1}^{n} |w_i|^q = \sum _{i=1}^{n} \left| \frac{1}{n}\right| ^q = n^{1-q} . \end{aligned}$$

As $\ell _1= \Vert \varvec{w}\Vert _1 = \sum _{i=1}^{n} |w_i| =1$, $i=1,\dots ,n$, the following relationship between norms holds then true:

$$\begin{aligned} 1 = \Vert \varvec{w}\Vert _1 \le \Vert \varvec{w}\Vert _q^q \le n^{1-q} . \end{aligned}$$

In fact, from norm inequalities, if $0< q < p$, we know

$$\begin{aligned} \Vert \varvec{w}\Vert _p \le \Vert \varvec{w}\Vert _q \le n^{1/q-1/p}\Vert \varvec{w}\Vert _p . \end{aligned}$$

(B-3)

Then, if $p=1$ and $0<q \le 1$

$$\begin{aligned} \Vert \varvec{w}\Vert _1 \le \Vert \varvec{w}\Vert _q \le n^{1/q-1}\Vert \varvec{w}\Vert _1 \end{aligned}$$

or, equivalently

$$\begin{aligned} 1 \le \Vert \varvec{w}\Vert ^q_q \le n^{1-q} \ \end{aligned}$$

as we have that $\Vert \varvec{w}\Vert _1 =1$ when $0 \le w_i \le 1$ and $\sum _{i=1}^{n} w_1 =1$. $\square$

Let $R(\varvec{w})=\varvec{w}'\varvec{\varSigma } \varvec{w}$, and $\varvec{w}$ and $\varvec{w}_{opt}$ be the theoretical and empirical optimal allocation vectors that solve the optimization problems

$\varvec{w}= \hbox {argmin}_{\mathbf{1'}{\varvec{w}} = 1, \Vert \varvec{w}\Vert _q^q\ \le c^q} \varvec{w}'\varvec{\varSigma } \varvec{w}$ and $\varvec{w}_{opt} = \hbox {argmin}_{\mathbf{1'}{\varvec{w}} = 1, \Vert \varvec{w}\Vert _q^q\ \le c^q} \varvec{w}'\widehat{\varvec{\varSigma } }\varvec{w}$, where $\varvec{\varSigma }$ and $\hat{\varvec{\varSigma } }$ are the theoretical covariance matrix and its estimate, respectively.

Proposition 3

Let $a_n$ represent the maximum component-wise estimation error, i.e., $a_n = \Vert \hat{\varvec{\varSigma } } - \varvec{\varSigma } \Vert _{\infty }$. Then, under the assumptions in Fan et al. (2012), we can write the oracle, empirical and actual risks as

$$\begin{aligned} |R(\varvec{w}) - R_n(\varvec{w}_{opt})|&\le a_n c^2 \\ |R(\varvec{w}_{opt}) - R_n(\varvec{w}_{opt})|&\le a_n c^2 \\ |R(\varvec{w}_{opt}) - R(\varvec{w})|&\le 2a_n c^2 . \end{aligned}$$

These inequalities hold without any condition on the weights and show that the differences between oracle, empirical and actual risks are very small as long as c is not too large and the covariance estimate is precise.

Proof

Proof of Proposition 3 First, let us recall Theorem 1 in Fan et al. (2012), which states the following relationships between oracle, empirical and actual risk of a constrained minimum variance portfolio $\varvec{w}$, with $\Vert \varvec{w}\Vert _q \ \le c$ (i.e., $\root q \of {\ell _q}\ \le c$)

$$\begin{aligned} |R_n(\varvec{w}) - R(\varvec{w})|&\le a_n c^2 \\ |R(\varvec{w}) - R_n(\varvec{w}_{opt})|&\le a_n c^2 \ \\ |R(\varvec{w}_{opt}) - R(\varvec{w})|&\le 2a_n c^2 . \end{aligned}$$

From Eq. (B-3), if $p=1$ and $0<q \le 1$, we know

$$\begin{aligned} \Vert \varvec{w}\Vert _1\ \le \Vert \varvec{w}\Vert _q \end{aligned}$$

or, equivalently

$$\begin{aligned} \ell _1 \le \root q \of {\ell _q} . \end{aligned}$$

As we solve the optimization problem (B-1) for $\Vert \varvec{w}\Vert _q^q \le c^q$, $\Vert \varvec{w}\Vert _1 \le c$. The bounds on the differences between oracle, empirical, and actual risks, reported in Theorem 1 in Fan et al. (2012), still hold. $\square$

Table 6 Average penalized minimum variance (objective function) and computational time (in seconds) of gradient projection (GP) and coordinate-descent (CD) algorithms, over 10 values of $\lambda$ within the interval $[9\times 10^{-7};\ 9\times 10^{-6}]$

Appendix C: Optimization methods and computational time

In this section, we compare the performance of two state-of-art methods in non-convex optimization in solving Problem 8: the gradient projection (GP) algorithm, developed by Figueiredo et al. (2007), and the cycling coordinate descent (CD) algorithm, implemented by Yen and Yen (2014). The corresponding pseudo-codes are described in Algorithms 1 and 2. We run the two methods for the $\ell _q$ and Log-penalties in both dataset over the whole sample period, using a vector of 10 $\lambda$s, as specified in Sect. 3.2. Table 6 reports the average penalized minimum variance obtained by the two algorithms, as in Eq. (4) (Columns 2 and 3), and the corresponding computational time (Columns 5 and 6). The comparison is implemented in Matlab R2016.a on a Lenovo ThinkPad X1 Yoga laptop with 2.50 GHz, Intel Core i7-6500U processor in Windows 10. We confirm empirically the results of Gasso et al. (2009) and find that the gradient projection outperforms the cycling coordinate descent, achieving lower or equal values of penalized variance for any value of $\lambda$ (Column 4), and is more efficient in terms of time, especially when the dimensionality of the data increases. For a comparison between the performance of state-of-art methods in non-convex optimization, we refer to Giuzio (2017) and references therein.

Appendix D: Transaction costs

As the magnitude of portfolio weights is a proxy for transaction costs (Brodie et al. 2009), we model these costs as a payment proportional to the transaction volume (i.e., turnover) by the factor v. Results do not change qualitatively when considering $v = 0.10$ and $v = 0.25$, as Tables 7 and 8 show.

$$\begin{aligned} \text {Cost}_t = \sum _{i=1}^{n} v |w_{i,t} - w_{i,t-1}|R_{i,t} \end{aligned}$$

Table 7 Average statistics of the different portfolios, adjusted for transaction costs (10 bps), on S&P 100 and S&P 500: OOS annual net risk, OOS annual net return, OOS annual net Sharpe Ratio, annual net Value-at-Risk, annual net Expected Shortfall

Table 8 Average statistics of the different portfolios, adjusted for transaction costs (25bps), on S&P 100 and S&P 500: OOS annual net risk, OOS annual net return, OOS annual net Sharpe Ratio, annual net Value-at-Risk, annual net Expected Shortfall