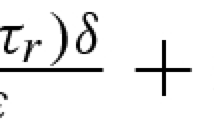Local and global indeterminacy and transition dynamics in a growth model with public goods

Abstract

This paper studies local and global indeterminacy and transition dynamics in an endogenous growth model where public goods increase production and the household’s utility. We study the impact on economic growth in the face of valuing public goods and socially conscious economic agents. When public goods are undervalued, the economy steadily converges to a unique low-growth equilibrium. As the utility share of public goods increases, another equilibrium emerges, but the difference between the two growth rates, “low” and “high”, narrows until both equilibria coalesce and disappear, producing a scenario with no convergence on a balanced growth path (BGP). The low-growth equilibrium is stable, and there may be monotonic convergence toward a broadly stable high-growth equilibrium. The economy may also oscillate between growth rates before reaching the high-growth BGP, or may diverge from it. In addition, before the high-growth BGP becomes unstable, the model may exhibit an unstable limit cycle that surrounds it. Moreover, if social consciousness co-varies with the weight of public goods on utility, a homoclinic orbit may emerge that links the low-growth equilibrium to itself.

Appendices

Appendix 1

1.1 Mathematical proofs

Derivation of the Jacobian matrix in (22): The two-dimensional system (14) is equivalent to

$$\begin{aligned} \dot{x} &=\frac{\dot{x}}{x} \cdot x \\& =\left\{ \frac{\beta (1-\theta )[(\gamma +\tau -1)z^{\alpha } -\eta ] +\alpha (1-\tau ) z^{\alpha -1} -\rho + (\gamma -1)\eta }{\theta } - (1-\tau ) z^{\alpha -1}+x + \eta \right\} x, \\ \dot{z} &=\frac{\dot{z}}{z} \cdot z \\ &=\left\{ (1-\tau ) z^{\alpha -1} -x - (\gamma +\tau -1)z^{\alpha } \right\} z. \end{aligned}$$

The Jacobian matrix of the system is given by

$$J = \begin{bmatrix} a_{11} &{} a_{12} \\ a_{21} &{} a_{22} \end{bmatrix},$$

where

$$\begin{aligned} a_{11}&= \frac{\partial \dot{x}}{\partial x} = \frac{\partial (\frac{\dot{x}}{x})}{\partial x} \cdot x + \frac{\dot{x}}{x} \cdot \underbrace{\frac{\partial (x)}{\partial x}}_{=1}&a_{12}&= \frac{\partial \dot{x}}{\partial z} = \frac{\partial (\frac{\dot{x}}{x})}{\partial z} \cdot x \\ a_{21}&= \frac{\partial \dot{z}}{\partial x} = \frac{\partial (\frac{\dot{z}}{z})}{\partial x} \cdot z&a_{22}&= \frac{\partial \dot{z}}{\partial z} = \frac{\partial (\frac{\dot{z}}{z})}{\partial z} \cdot z + \frac{\dot{z}}{z} \cdot \underbrace{\frac{\partial (z)}{\partial z}}_{=1}. \end{aligned}$$

From the Jacobian matrix evaluated at the BGP, we have $\frac{\dot{x}}{x} \big |_{ss} = \frac{\dot{z}}{z} \big |_{ss} =0$ in (12) and (13). It follows that

$$\begin{aligned} a_{11}|_{ss}&= x^* \\ a_{12}|_{ss}&= \frac{\beta (1-\theta )(\gamma +\tau -1) \alpha z^*- (1-\tau )(1-\alpha )(\alpha -\theta )}{\theta } \, x^* (z^{*})^{\alpha -2} \\ a_{21}|_{ss}&= -z^* \\ a_{22}|_{ss}&=(1-\tau )(\alpha -1) (z^*)^{\alpha -1} - \alpha (\gamma +\tau -1)(z^*)^{\alpha }. \end{aligned}$$

Since

$$\begin{aligned} \frac{\dot{z}}{z} \Big |_{ss} =0 \ \Leftrightarrow \ (1-\tau ) (z^*)^{\alpha -1} = x^* + (\gamma +\tau -1)(z^*)^{\alpha } \end{aligned}$$

(32)

we rewrite

$$a_{22}|_{ss} = -(1-\alpha )x^* -(\gamma + \tau -1) (z^{*})^{\alpha }.$$

Accordingly,

$$\begin{aligned} J |_{ss}& \equiv J (x^*,z^*) \\ &=\begin{bmatrix} x^* &{} \dfrac{\beta (1-\theta )(\gamma +\tau -1) \alpha z^*- (1-\tau )(1-\alpha )(\alpha -\theta )}{\theta } \, x^* (z^{*})^{\alpha -2} \\ -z^* &{} -(1-\alpha )x^* -(\gamma + \tau -1) (z^{*})^{\alpha } \end{bmatrix}. \end{aligned}$$

$\square$

Proof of lemma 1

Consumption is non-negative if and only if $x=c/k\ge 0$. The function $x^{*}$ in (17) is continuous and strictly decreasing in g:

$$\frac{dx^*}{dg} =- \frac{(1-\alpha )(1-\tau )}{\alpha (\gamma +\tau -1)}\left( \frac{g+\eta }{\gamma +\tau -1} \right) ^{-\frac{1}{\alpha }} - 1 <0.$$

We conclude that $x^{*}$ is either always negative or becomes negative for $g > g_{\max }$ such that

$$x^*(g_{\max }) = 0 \ \Leftrightarrow \ (1-\tau ) \left( \frac{g_{\max }+\eta }{\gamma +\eta -1} \right) ^{\frac{\alpha -1}{\alpha }}=g_{\max }+\eta \ \Leftrightarrow \ g_{\max } = \frac{(1-\tau )^{\alpha }}{(\gamma +\tau -1)^{\alpha -1}} - \eta .$$

The latter case holds whenever $g_{\max }>0$, and thus $\eta <(1-\tau )^{\alpha } / (\gamma +\tau -1)^{\alpha -1}$

On the other hand, the function $z^{*}$ in (17) is continuous and strictly increasing in g:

$$\frac{dz^*}{dg} = \frac{1}{\alpha (\gamma +\tau -1)}\left( \frac{g+\eta }{\gamma +\tau -1} \right) ^{\frac{1}{\alpha }-1} >0.$$

It is easily seen that $x^* \in \left[ x^*(g_{\max }), x^*(0) \right)$ and $z^* \in \left[ z^*(0), z^*(g_{\max })\right)$ where:

$$\begin{aligned} x^*(g_{\max }) &= 0\quad \text{ and } \quad x^*(0) = (1-\tau )\left( \frac{\eta }{\gamma +\tau -1}\right) ^{\frac{\alpha -1}{\alpha }} -\eta , \\ z^*(0) &=\left( \frac{\eta }{\gamma +\tau -1}\right) ^{\frac{1}{\alpha }} \quad\text{ and } \quad z^*(g_{\max }) = \frac{1-\tau }{\gamma +\tau -1}. \end{aligned}$$

$\square$

Proof of proposition 1

For scenario (i), we have $\beta (\theta -1) + \theta \ge 0 \ \Leftrightarrow \ \beta (1-\theta ) \le \theta .$ Applying this inequality to the determinant of $J (x^*,z^*)$ leads to

$$\begin{aligned} \text {det}[J (x^*,z^*)] &= -(1 -\alpha ) (x^*)^2 - (\gamma +\tau -1) x^* (z^*)^{\alpha } \\&\quad+ \frac{\beta (1-\theta ) (\gamma +\tau -1) \alpha }{\theta } x^* (z^*)^{\alpha } - \frac{(1-\tau )(1-\alpha )(\alpha -\theta )}{\theta } x^* (z^*)^{\alpha -1} \\& \le -(1-\alpha ) (x^*)^2 - (1-\alpha ) (\gamma +\tau -1)x^*(z^*)^{\alpha } \\&\quad- \frac{(1-\tau )(1-\alpha )(\alpha -\theta )}{\theta } x^*(z^*)^{\alpha -1} \\ &= -(1-\alpha )x^* \left[ x^*+ (\gamma +\tau -1)(z^*)^{\alpha } \right] \\ &\quad- \frac{(1-\tau )(1-\alpha )(\alpha -\theta )}{\theta } x^*(z^*)^{\alpha -1} \\ &\underset{}{=} -(1-\alpha )(1-\tau )x^*(z^*)^{\alpha -1}- \frac{(1-\tau )(1-\alpha )(\alpha -\theta )}{\theta } x^*(z^*)^{\alpha -1} \\ &= -\frac{(1-\tau )(1-\alpha )\alpha }{\theta } x^*(z^*)^{\alpha -1}. \end{aligned}$$

Now $\text {det}[J (x^*,z^*)]<0$ and so the equilibrium is saddle-path stable. $\square$

Proof of proposition 2

Suppose that $g\in \mathcal {G}$. We can rewrite (27) as

$$\begin{aligned} \beta (g) = \frac{-\theta x^*(g) + (2-\gamma -\theta )\eta +\rho }{(1-\theta ) g}. \end{aligned}$$

(33)

Let $\beta >\theta /(1-\theta )$. We measure the rate of change of g with respect to a change in $\beta$ through the functions $\Gamma$ and $\Psi$ in (19)–(20). Note that in the case where $\Gamma$ and $\Psi$ intersect twice, say at $g_h<g_l$, we must have $\beta (g_l) = \beta (g_h)$. Reciprocally, the variations of $g_l$ and $g_h$ with respect to $\beta$ are in opposite directions.

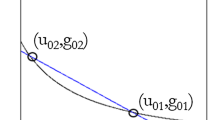
When $\beta$ increases, the slope of $\Psi$ is larger in absolute value, which means a steeper downward tilt to the line. From Fig. 13 this corresponds to going from one long-run equilibrium solution to two equilibria that further collide and disappear.²⁵ We find that the value of $g_l$ [resp. $g_h$] is increasing [resp. decreasing] as the slope of $\Psi$ becomes more negative, i.e., $\beta$ increases. From Lemma 1 the system admits a unique relevant equilibrium whenever $g_l< g_{\max } < g_h$, and so $\beta (g_l)=\beta (g_h)<\beta (g_{\max })$. Set $\check{\beta } = \beta (g_{\max })$. Plugging (21) and $x^*(g_{\max })=0$ into (33), we get

$$\check{\beta } = \frac{(2-\gamma -\theta )\eta + \rho }{(1-\theta )\left[ (\gamma +\tau -1)\left( \frac{1-\tau }{\gamma +\tau -1}\right) ^{\theta }-\eta \right] }.$$

Fig. 13

Illustration of scenario (ii) with $\beta _1< \beta _2< \beta _3 < \beta _4$: the value of $\beta _1$ produces only one relevant equilibrium; the value of $\beta _2$ produces multiple equilibria; the value of $\beta _3$ produces two coincident equilibria; and the value of $\beta _4$ produces no equilibria

Now the critical value of $\beta$ giving rise to the coalescence equilibrium for some $\widetilde{g} \equiv g_l= g_h \in \mathcal {G}$ satisfies simultaneously $\frac{d \beta }{d g} \big |_{g=\tilde{g}}=0$ and $\text {det}[J(x^*,z^*)] = 0$. Given (27) it follows that

$$\begin{aligned}\frac{d \beta }{d g} &= \frac{ (\theta \eta + g)(1-\tau ) \left( \frac{g+\eta }{\gamma +\tau -1}\right) ^{\frac{\theta -1}{\theta }} - (g +\eta ) [ (2-\gamma )\eta + \rho ]}{(1-\theta )g^2 (g+\eta )} = 0 \\& \Leftrightarrow (\theta \eta + g)(1-\tau ) \left( \frac{g+\eta }{\gamma +\tau -1}\right) ^{\frac{\theta -1}{\theta }} - (g +\eta ) [ (2-\gamma )\eta + \rho ] = 0 \\ &\! \underset{g\in \mathcal {G}}{\Leftrightarrow } \,(\theta \eta + g) \big \{ [-\beta (1-\theta ) +\theta ]g + (2-\gamma ) \eta +\rho \big \} - \theta (g +\eta ) [ (2-\gamma )\eta + \rho ] =0 \\ &\Leftrightarrow \widetilde{\beta } \equiv \beta = \frac{(1-\theta )[(1-\gamma -\theta )\eta + \rho ] +\eta +\theta \widetilde{g}}{(1-\theta )(\theta \eta + \widetilde{g})}. \end{aligned}$$

From (25) we obtain

$$\text {det}[J (x^*,z^*) ] = 0 \ \Leftrightarrow \ x^* \left\{ -(1-\theta )x^* + [\beta (1-\theta )-1] (\gamma +\tau -1)(z^*)^{\theta }\right\} =0.$$

Of course $\widetilde{g} \ne g_{\max }$ and the required solution is

$$x^* = \frac{\beta (1-\theta )-1}{1-\theta } (\gamma +\tau -1)(z^*)^{\theta } \underset{(17)}{=} \frac{\beta (1-\theta )-1}{1-\theta } (\widetilde{g} + \eta ).$$

We replace the latter into $\frac{\dot{z}}{z}\big |_{ss}=0$ yielding

$$z^* = \frac{1-\theta }{\beta (1-\theta )-\theta } \frac{1-\tau }{\gamma +\tau -1}.$$

$\square$

Proof of proposition 5

The saddle-node bifurcation requires three conditions on the system, see Guckenheimer and Holmes (2002, Theorem 3.4.1). When $\beta =\widetilde{\beta }$, there is an equilibrium $(x^*,z^*)=(\widetilde{x}^*,\widetilde{z}^*)$ for which the following hypotheses are satisfied:

• (SN1) $J(\widetilde{x}^*,\widetilde{z}^*) \big |_{\beta =\widetilde{\beta }}$ has a simple eigenvalue $\lambda =0$ with right eigenvector $\mathbf {v}^\text {T}=(v_1,v_2)$ and left eigenvector $\mathbf {w}^\text {T}=(w_1,w_2)$;

• (SN2) $\mathbf {w}^\text {T} F_{\beta } (\widetilde{x}^*;\widetilde{z}^*;\widetilde{\beta }) \ne 0$, where $F_{\beta }$ is the vector of partial derivatives with respect to $\beta$;

• (SN3) $\mathbf {w}^\text {T} \left[ D^2 F (\widetilde{x}^*,\widetilde{z}^*;\widetilde{\beta }) (\mathbf {v},\mathbf {v})\right] \ne 0$.

Condition (SN1) is equivalent to $\text {det}[J(\widetilde{x}^*,\widetilde{z}^*)]\big |_{\beta =\widetilde{\beta }} =0$, which is immediate from the proof of Proposition 2 with $\widetilde{x}= \frac{\widetilde{\beta }(1-\theta )-1}{1-\theta } (\gamma +\tau -1)(\widetilde{z}^*)^{\theta }$. We find that:

$$\mathbf {v}^\text {T} = \big ( (1-\theta ) \widetilde{x}^* + (\gamma +\tau -1)(\widetilde{z}^*)^{\theta }, \ \widetilde{z}^* \big ) \quad \text { and } \quad \mathbf {w}^\text {T} = \left( \widetilde{z}^*,\ \widetilde{x}^*\right) .$$

Moreover,

$$\mathbf {w}^\text {T} F_{\beta } (\widetilde{x}^*;\widetilde{z}^*;\widetilde{\beta }) = \frac{1-\theta }{\theta } \left[ (\gamma +\tau -1)(\widetilde{z}^*)^\theta - \eta \right] \widetilde{z}^* \underset{(17)}{=} \frac{1-\theta }{\theta } \, \widetilde{g} \, \widetilde{z}^*$$

and

$$\begin{aligned} \mathbf {w}^\text {T} \big [ D^2&F (\widetilde{x}^*,\widetilde{z}^*;\widetilde{\beta }) (\mathbf {v},\mathbf {v})\big ] \\&= (\gamma +\tau -1) [\beta (1-\theta ) - 1] (\widetilde{z}^*)^{2\theta } \left[ \frac{\theta - \beta (1-\theta )}{1-\theta } (\gamma +\tau -1) \widetilde{z}^* - (1-\tau ) \theta \right] . \end{aligned}$$

Lemma 2 in Appendix 2 guarantees that $\widetilde{g}\ne 0$ and $\widetilde{z}^*\ne 0$ and hence (SN2) holds true. In addition, given (29), it follows easily that conditions (SN3) also holds true.

Proof of proposition 6

Suppose that the Jacobian matrix in (22) admits a pair of conjugate complex eigenvalues $v(\beta )\pm i \omega (\beta )$ for the high-growth equilibrium $(x_h, z_h)$. We thus get

$$v(\beta ) =\frac{ \text {tr}[J(x_h,z_h)]}{2}, \qquad \omega (\beta ) = \frac{\sqrt{-\{\text {tr}[J(x_h,z_h)]\}^2 +4\text {det}[J(x_h,z_h)]}}{2}.$$

If, for some $\beta =\beta _f$, we verify the following hypotheses:

$$\text {(H1) }\omega (\beta _f) \equiv \omega _0 \ne 0; \quad \text { (H2) }v(\beta _f)=0;\quad \text { (H3) }\frac{d v}{d \beta } \Big |_{\beta =\beta _f}\ne 0;$$

then the pair of eigenvalues cross the imaginary axis at non-zero speed, see Guckenheimer and Holmes (2002, Theorem 3.4.2).

• 1. Condition (H1) is automatically satisfied by imposition of condition (H2). Condition (H2) holds when:

  $$\begin{aligned} v(\beta ) =0 \ \Leftrightarrow \ \text {tr}[J(x_h,z_h)]=0 \ \Leftrightarrow \ x_h = \frac{\gamma +\tau -1}{\theta } z_h^{\theta }. \end{aligned}$$

  (34)

  Taking $x_h$ replaced by (34) into $\frac{\dot{z}}{z}\big |_{ss}=0$ in (13) yields

  $$x_h = \frac{\gamma +\tau -1}{\theta } \left( \frac{\theta }{1+\theta } \frac{1-\tau }{\gamma +\tau -1}\right) ^{\theta } \quad \text { and } \quad z_h = \frac{\theta }{1+\theta } \frac{1-\tau }{\gamma +\tau -1}.$$

  From $\frac{\dot{x}}{x}\big |_{ss}=0$ in (12) we can write

  $$\begin{aligned}x_h &= (1-\tau ) z_h^{\theta -1} - \eta - \frac{1}{\theta } [ \beta (1-\theta )\left[ (\gamma +\tau -1)z_h^{\theta }-\eta \right] \\&\quad+\theta (1-\tau )z^{\theta -1}-\rho -(2-\gamma )\eta ] .\end{aligned}$$

  Substituting $x_h$ into (34) leads to

  $$- \theta \eta - \beta (1-\theta )\left[ (\gamma +\tau -1)z_h^{\theta }-\eta \right] + \rho + (2-\gamma )\eta = (\gamma +\tau -1) z_h^{\theta }.$$

  Together with $z_h$ in (17) we obtain

  $$\beta _f \equiv \beta = \frac{\rho + (2-\gamma -\theta ) \eta - (\gamma +\tau -1) z_h^{\theta }}{(1-\theta )\left[ (\gamma +\tau -1)z_h^{\theta } - \eta \right] } = \frac{\rho + (1-\gamma -\theta ) \eta - g_h}{(1-\theta )g_h} .$$

• 2. Next, we differentiate $v(\beta )$ with respect to $\beta$, where

  $$\begin{aligned} v(\beta ) \ \underset{}{=}&\ \frac{1}{2} \left[ \theta x_h -(\gamma +\tau -1) z_h\right] \ \\ \underset{}{=}&\ \frac{1}{2} \left[ \theta (1-\tau ) \left( \frac{g_h+\eta }{\gamma +\tau -1} \right) ^{\tfrac{\theta -1}{\theta }}-(1+\theta )(g_h+\eta ) \right] . \end{aligned}$$

  Recall that $g_h \equiv g_h(\beta )$ follows from (18) such that

  $$\theta (1-\tau )\left( \dfrac{g_h+\eta }{\gamma +\tau -1}\right) ^{\tfrac{\theta -1}{\theta }} = g_h\left[ -\beta (1-\theta )+\theta \right] +\left( 2-\gamma \right) \eta +\rho .$$

  By differentiating the latter with respect to $\beta$ we find $\frac{dg_h}{d\beta }$:

  $$\begin{aligned} -\frac{(1-\tau )(1-\theta )}{\gamma +\tau -1}\left( \frac{g_h+\eta }{\gamma +\tau -1}\right) ^{-\tfrac{1}{\theta }} \frac{dg_h}{d\beta }&= \frac{dg_h}{d\beta } \left[ -\beta (1-\theta )+\theta \right] - g_h(1-\theta ) \\ \Leftrightarrow \ \frac{dg_h}{d\beta }&= \frac{g_h(1-\theta )}{- \beta (1-\theta ) + \theta +\frac{(1-\tau )(1-\theta )}{\gamma +\tau -1}\left( \frac{g_h+\eta }{\gamma +\tau -1}\right) ^{-\frac{1}{\theta }}}. \end{aligned}$$

  Therefore,

  $$\frac{d v}{d \beta } = \frac{1}{2} \left[ - \frac{(1-\theta ) (1-\tau )}{\gamma +\tau -1} \left( \frac{g_h+\eta }{\gamma +\tau -1} \right) ^{-\tfrac{1}{\theta }} -(1+\theta ) \right] \frac{d g_h}{d \beta }.$$

  Since $\theta \in (0,1)$ and $g_h>0$, we have for all $\beta >0$:

  $$\frac{d g_h}{d \beta } \ne 0, \qquad - \frac{(1-\theta ) (1-\tau )}{\gamma +\tau -1} \left( \frac{g_h+\eta }{\gamma +\tau -1} \right) ^{-\tfrac{1}{\theta }} -(1+\theta )<0.$$

  Consequently $\frac{d v}{d \beta } \ne 0$. We conclude that in an open neighbourhood of $\beta _f$ the eigenvalues of the Jacobian matrix at $(x_{h},z_{h})$ cross the imaginary axis at non-zero speed and a bifurcation occurs at $\beta _f$.

• 3. If an additional genericity condition is satisfied, then the model undergoes a Hopf bifurcation at $\beta =\beta _f$ (Marsden and McCracken 1976; Guckenheimer and Holmes 2002). Let us rewrite the two-dimensional system underlying (14) as:

  $$\begin{aligned} \dot{x}&= f(x,z;\beta )\\ \dot{z}&= g(x,z;\beta ). \end{aligned}$$

  The first Lyapunov coefficient from the third Taylor expansion on the centre manifold of the linearised system is given by:

  $$\begin{aligned} a =&\ \frac{1}{16}(f_{xxx}+f_{xzz}+g_{xxz}+g_{zzz})\\&+ \dfrac{1}{16\omega _0}\left[ f_{xz}\left( f_{xx}+f_{zz}\right) -g_{xz}\left( g_{xx}+g_{zz}\right) -f_{xx}g_{xx}+f_{zz}g_{zz}\right] \end{aligned}$$

  where $\omega _0 \equiv \omega (\beta _f)$ and $f_{xz} = \frac{\partial ^2 f}{\partial x y} \big |_{\beta =\beta _f}(x_h,z_h)$, etc. Then, a simplifies to:

  $$\begin{aligned} a= &\frac{1}{16} \left\{ (\gamma +\tau -1)[\theta ^2+\theta -\beta _f(1-\theta )]z_h^{\theta -2}+\theta (2-\theta )(1-\tau ) z_h^{\theta -3}\right\} (1-\theta ) \\ &+\frac{1}{16 \omega _0} \big \{\beta _f (1-\theta )^2 (\gamma +\tau -1)^2 [\theta ^2+\theta -\beta _f(1-\theta )] x_h z_h^{2\theta -3} \\&+ \theta \beta _f (1-\theta )^3 (1-\tau )(\gamma +\tau -1) x_h z_h^{2\theta -4} - (\gamma +\tau -1) [\theta ^2+\theta \\&-\beta _f(1-2\theta )] z_h^{\theta -1}-\theta (1-\theta )(1-\tau )z_h^{\theta -2} \big \}. \end{aligned}$$

  According to Guckenheimer and Holmes (2002), a small amplitude limit cycle exists if the genericity condition holds, i.e., $a\ne 0$. Otherwise, we say that the bifurcation is degenerate, which concludes the proof. $\square$

Proof of proposition 7

We are required to show that there exists a region in the $(\beta ,\gamma )$-parameter space such that the system (14) admits an equilibrium $(x^*,z^*)$ for which the Bogdanov-Takens condition is satisfied:

• (BT) $\text {tr}[J(x^*,z^*)]=\text {det}[J(x^*,z^*)]=0$.

Parameters combinations in Propositions 2 and 6 ensure that this can happen at a coalescence equilibrium such that

$$\left\{ \begin{aligned} \theta x^* - (\gamma +\tau -1) (z^*)^{\theta }&=0 \\[0.1cm] -(1-\theta )x^* + [\beta (1-\theta )-1] (\gamma +\tau -1)(z^*)^{\theta }&=0 \end{aligned}\right.$$

implies

$$-\frac{1-\theta }{\theta } + \beta (1-\theta )-1 \ \Leftrightarrow \ \beta _\text {BT} \equiv \beta =\frac{1}{\theta (1-\theta )}.$$

On the other hand, we have $\beta _f= \beta _\text {BT}$ in (30) and hence $\gamma _\text {BT}\equiv \gamma$ is implicitly determined from

$$(\gamma +\tau -1 )\left( \frac{\theta }{1+\theta } \frac{1-\tau }{\gamma +\tau -1} \right) ^{\theta } = \frac{(1+2\theta -\theta ^2 -\theta \gamma )\eta + \theta \rho }{1+\theta }.$$

Appendix 2

1.1 Properties

By Lemma 1, we have $g\in \mathcal {D}_{g^*} = (0,g_{\max }]$, $x^* \in \mathcal {D}_{x^*} =\left[ 0,x^*_{\max }\right)$ and $z^*\in \mathcal {D}_{z^*} =\left( z^*_{\min },z^*_{\max } \right]$. For each value of $z^*$ it is convenient to think of $\text {tr}[J (x^*,z^*)]$, $\text {det}[J (x^*,z^*) ]$ and $\Delta (x^*,z^*)$ as functions of $x^*$. We list the properties of these functions.

Fig. 14

Illustration of trace, determinant and discriminant of $J(x^*,z^*)$ as functions of g. The red line is associated with $(x_l,z_l)$ and the blue line is associated with $(x_h,z_h)$

Properties of $\text {tr}[J(x^*,z^*)]$: We see that $\text {tr}[J (x^*,z^*)]$ is linear in $x^*$ and

• $\dfrac{\partial \text {tr}[J(x^*,z^*)]}{\partial x^*} = \theta >0$ for all $x^* \in \mathcal {D}_{x^*}$;

• $\text {tr}[J (x^*,z^*) ] =0 \ \Leftrightarrow \ \widehat{x}^* \equiv x^* = \dfrac{\gamma +\tau -1}{\theta } (z^*)^{\theta }$;

• $\text {tr}[J (x^*,z^*) ] < 0$ for all $x^* \in [0,\widehat{x}^*)$ and $\text {tr}[J (x^*,z^*) ] > 0$ for all $x^* \in (\widehat{x}^*,x^*_{\max })$.

Properties of $\text {det}[J (x^*,z^*)]$: We see that $\text {det}[J (x^*,z^*)]$ is a real quadratic polynomial in $x^*$ and

• $\begin{aligned}\dfrac{\partial \text {det}[J (x^*,z^*)]}{{\partial x^*}} = 0 & \Leftrightarrow -2(1-\theta ) x^*+[\beta (1-\theta )-1] (\gamma +\tau -1)(z^*)^{\theta }=0 \\ &\Leftrightarrow \bar{x}^* \equiv x^* = \frac{\beta (1-\theta )-1}{2(1-\theta )} (\gamma +\tau -1)(z^*)^{\theta };\end{aligned}$  

• $\dfrac{\partial \text {det}[J (x^*,z^*)]}{{\partial x^*}} > 0$ for all $x^* \in [0,\bar{x}^*)$ and $\dfrac{\partial \text {det}[J (x^*,z^*)]}{{\partial x^*}} < 0$ for all $x^* \in (\bar{x}^*, x^*_{\max })$;

• $\begin{aligned}\text {det}[J (x^*,z^*) ] =0 & \Leftrightarrow x^* \left\{ -(1-\theta )x^* + [\beta (1-\theta )-1] (\gamma +\tau -1)(z^*)^{\theta }\right\} =0 \\& \Leftrightarrow x^*=0 \ \vee \ \widetilde{x}^* \equiv x^* = \frac{\beta (1-\theta )-1}{1-\theta } (\gamma +\tau -1)(z^*)^{\theta }; \end{aligned}$  

• $\text {det}[J (x^*,z^*) ] > 0$ for all $x^* \in (0,\widetilde{x}^*)$ and $\text {det}[J (x^*,z^*) ] < 0$ for all $x^* \in (\widetilde{x}^*,x^*_{\max })$.

Properties of $\Delta (x^*,z^*)$: We see that $\Delta (x^*,z^*)$ is a real quadratic polynomial in $x^*$ and

• $\begin{aligned} \dfrac{\partial \Delta (x^*,z^*)}{{\partial x^*}}&= 0 \\ &\Leftrightarrow 2(2-\theta )\left[ (2-\theta )x^* + (\gamma +\tau -1) (z^*)^{\theta } \right] \\&\quad- 4\beta (1-\theta )(\gamma +\tau -1)(z^*)^{\theta } =0 \\& \Leftrightarrow (2-\theta )^2 x^* - [ 2\beta (1-\theta ) - 2 + \theta ] (\gamma + \tau -1)(z^*)^{\theta } =0 \\ &\Leftrightarrow \bar{\bar{x}}^* \equiv x^* =\frac{2\beta (1-\theta ) - 2 + \theta }{(2-\theta )^2} (\gamma + \tau -1)(z^*)^{\theta }; \end{aligned}$  

• $\dfrac{\partial \Delta (x^*,z^*)}{{\partial x^*}} < 0$ for all $x^* \in [0,\bar{\bar{x}}^*)$ and $\dfrac{\partial \Delta (x^*,z^*)}{{\partial x^*}} > 0$ for all $x^* \in (\bar{\bar{x}}^*, x^*_{\max })$;

• $\begin{aligned} \Delta (x^*,z^*)&=0 \Leftrightarrow \left[ (2-\theta )x^* + (\gamma +\tau -1) (z^*)^{\theta } \right] ^2\\& \quad- 4\beta (1-\theta )(\gamma +\tau -1) x^*(z^*)^{\theta } = 0 \\ &\Leftrightarrow (2-\theta )^2 (x^*)^2 - 2 \left[ 2\beta (1-\theta ) - 2 +\theta \right] (\gamma + \tau -1) x^* (z^*)^\theta \\&\quad+ (\gamma + \tau -1)^2 (z^*)^{2\theta } = 0. \end{aligned}$  

  This yields a quadratic equation in $x^*$ whose discriminant is:

  $$16 \beta [\beta (1-\theta ) - 2 + \theta ](1-\theta ) (\gamma +\tau -1)^2(z^*)^{2\theta } \gtreqqless 0 \ \Leftrightarrow \ \beta \gtreqqless \frac{2-\theta }{1-\theta };$$

• If $\dfrac{1}{1-\theta }<\beta < \dfrac{2-\theta }{1-\theta }$, then $\Delta (x^*,z^*) > 0$ for all $x^* \in \mathcal {D}_{x^*}$;

• If $\beta> \dfrac{2-\theta }{1-\theta } = 1 +\dfrac{1}{1-\theta }> \dfrac{1}{1-\theta }$, then

  $$\begin{aligned} \Delta (x^*,z^*)& = 0 \\ \Leftrightarrow x^*_{\pm } &= \frac{2\beta (1-\theta ) - 2 +\theta \pm 2\sqrt{\beta [\beta (1-\theta ) - 2 + \theta ](1-\theta )} }{(2-\theta )^2}(\gamma +\tau -1) (z^*)^\theta \end{aligned}$$

  and

  $$\begin{aligned} \Delta (x^*,z^*) > 0&\text { for all } x^* \in [0,x^*_-) \cup (x^*_+,x^*_{\max }), \\ \Delta (x^*,z^*) < 0&\text { for all } x^* \in (x^*_-,x^*_+). \end{aligned}$$

From the relation between $x^*$ and g (hence $z^*$ and g) we can draw the graph of $\text {tr}[J (x^*,z^*)]$, $\text {det}[J (x^*,z^*) ]$ and $\Delta (x^*,z^*)$ as functions of g, see Fig. 14, and the following statements are immediate.

Lemma 2

If $\beta >\frac{1}{1-\theta }$, then $0< \widehat{x}^*< \widetilde{x}^*< \check{x}^* < x^*_{\max }$, and $g_{\max }> \widehat{g}> \widetilde{g}> \check{g} > 0$, and $z^*_{\max }> \widehat{z}^*> \widetilde{z}^*> \check{z}^* > z^*_{\min }$. If $\beta > 1+\frac{1}{1-\theta }$, then $0< x^*_{-}< x^*_{+}< \widehat{x}^*< \widetilde{x}^*< \check{x}^* < x_{\max }$, and $g_{\max }> g_{+}> g_{-}> \widehat{g}> \widetilde{g}> \check{g} > 0$, and $z^*_{\max }> z^*_{+}> z^*_{-}> \widehat{z}^*> \widetilde{z}^*> \check{z}^* > z^*_{\min }.$

Appendix 3

1.1 Government and taxes

Governments may compensate for low social awareness or a low weight of public goods in utility by increasing taxes $\tau$ and thus promoting the creation of more public goods. Suppose again that households care little about public goods such that $\beta$ is low and there is a unique long-run equilibrium. Differentiating $\Gamma$(g) with respect to $\tau$ yields:

$$\dfrac{\partial \Gamma (g,\tau )}{\partial \tau }=-\frac{(\alpha \gamma +\tau -1)\left( \frac{g+\eta }{\gamma +\tau -1}\right) ^{\frac{\alpha -1}{\alpha }}}{\gamma +\tau -1},$$

which is positive if $\alpha \in \left( 0,\bar{\alpha }\right)$, where $\bar{\alpha }=\tfrac{1-\tau }{\gamma }$ and negative if $\alpha \in \left( \bar{\alpha },1\right)$. In other words, the government can increase long-run growth by raising taxes, provided that the share of capital in production is not exceedingly high. Since $d\bar{\alpha }/d\tau >0$, $\bar{\alpha }$ also sets an upper bound for taxes above which more taxes will be detrimental to growth.

Let us assume now that there exist two equilibria. In this scenario, a higher $\tau$ shifts $\Gamma (g)$ rightwards if $\alpha <\bar{\alpha }$. This yields a lower high-growth BGP rate, which is compensated by an increase in the BGP growth rate at the low-growth equilibrium.²⁶ Therefore, the government may play an important role in stabilizing growth rates under multiple equilibria.

Fig. 15

Change in the stability of the high-growth equilibrium along a smooth path where $\tau$ increases. Parameter values are reported in Table 1 and $\beta =5$. The vertical dashed lines delimit different stability regions of the equilibrium

From Fig. 15, we observe that a smooth increase in taxes bears the same qualitative implications as increases in $\beta$ or $\gamma$. First, it would shift the economy from a monotonic path (region 1) converging on high-growth (recall Table 1) towards an oscillating one (region 2), with a lower high-growth rate at the BGP. If the government increases taxes further, it may lead to a point where high-growth becomes unstable and the economy converges along the stable-arm towards a low growth equilibrium (region 3) that is higher than the initial one. Finally, if $\tau >\tau _c$, the two equilibria collide and disappear and there is no BGP.

We thus conclude that, under multiple equilibria, governments may be effective at stabilizing growth through the creation of public goods. As mentioned before, stabilizing growth in the present context corresponds either to reducing the gap between growth rates or placing the economy on monotonic instead of oscillatory convergence. From a social point of view, such stabilization may or may not be desirable. For a normative analysis, a criterion would have to be defined to analyze social welfare along the different transition paths.