Skip to main content
SpringerLink
Log in

Approximate Analytical Solution of the Generalized Kolmogorov-Petrovsky-Piskunov Equation with Cubic Nonlinearity

  • Published:
Acta Mathematicae Applicatae Sinica, English Series Aims and scope Submit manuscript

Abstract

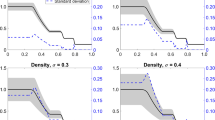
In this paper, the approximate analytical oscillatory solutions to the generalized Kolmogorov-Petrovsky-Piskunov equation (gKPPE for short) are discussed by employing the theory of dynamical system and hypothesis undetermined method. According to the corresponding dynamical system of the bounded traveling wave solutions to the gKPPE, the number and qualitative properties of these bounded solutions are received. Furthermore, pulses (bell-shaped) and waves fronts (kink-shaped) of the gKPPE are given. In particular, two types of approximate analytical oscillatory solutions are constructed. Besides, the error estimations between the approximate analytical oscillatory solutions and the exact solutions of the gKPPE are obtained by the homogeneity principle. Finally, the approximate analytical oscillatory solutions are compared with the numerical solutions, which shows the two types of solutions are similar.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Ablowitz, M.J., Zeppetella, A. Explicit solutions of Fishers equation for a special wave speed. Bulletin of Mathematical Biology, 41(6): 835–840 (1979)

    Article  MathSciNet  MATH  Google Scholar 

  2. Aronson, D.G., Weinberger, H.F. Nonlinear diffusion in population genetics, combustion, and nerve pulse propagation. Partial Differential Equations and Related Topics, Berlin, Heidelberg, Springer, 1975

    Google Scholar 

  3. Britton, N.F. Reaction-diffusion equations and their applications to biology. Academic Press, London, 1986

    MATH  Google Scholar 

  4. Bramson, M. Convergence of solutions of the Kolmogorov equation to travelling waves. Memoirs of the American Mathematical Society, 285(1): 8–31 (1983)

    MathSciNet  MATH  Google Scholar 

  5. Berestycki, H., Hamel, F. Reaction-diffusion equations and propagation phenomena. Applied Mathematical Sciences. Springer-Verlag, New York, 2008

    Google Scholar 

  6. Chou, Y. Measuring the orbital periods of low mass X-ray binaries in the X-ray band. Research in Astronomy and Astrophysics, 14(11): 1367–1382 (2014)

    Article  Google Scholar 

  7. Cantrell, R.S., Cosner, C. Spatial ecology via reaction-diffusion equations. Wiley Series in Mathematical and Computational Biology, John Wiley, Ltd., Chichester, 2003

    MATH  Google Scholar 

  8. EL-Hachem, M., Mccue, S.W., Jin, W., et al. Revisiting the Fisher-Kolmogorov-Petrovsky-Piskunov equation to interpret the spreading-extinction dichotomy. Proceedings of The Royal Society A Mathematical Physical and Engineering Sciences, 475(2229): 20190378 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  9. Fife, P.C. Mathmatical aspects of reacting and diffusing systems. Springer-Verlag, New York, 1979

    Book  MATH  Google Scholar 

  10. Feng, J.S., Li, W.J., Wan, Q.L. Using G’/G-expansion method to seek the traveling wave solution of Kolmogorov-Petrovskii-Piskunov equation. Applied Mathematics and Computation, 217(12): 5860–5865 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  11. Feller, W. An Introduction to Probability Theory and Applications, vols. I, II. John Wiley and Sons, 1966

  12. Grindrod, P. The Theory and Applications of Reaction-Diffusion Equations. 2nd ed. Oxford Applied Mathematics and Computing Science Series. The Clarendon Press Oxford University Press, New York, 1996

    MATH  Google Scholar 

  13. Gepreel, K.A. The homotopy perturbation method applied to the nonlinear fractional Kolmogorov-Petrovskii-Piskunov equations. Applied Mathematics Letters, 24(8): 1428–1434 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  14. Hamel, F. Qualitative properties of monostable pulsating fronts: exponential decay and monotonicity. Journal de Mathmatiques Pures et Appliquées, 89(4): 355–399 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  15. Hasnain, S., Saqib, M., Mashat, D.S. Two-Dimensional nonlinear reaction diffusion equation with time efficient scheme. American Journal of Computational Mathematics, 7(2): 183–194 (2017)

    Article  Google Scholar 

  16. Hattaf, K., Yousfi, N. Global stability for reaction-diffusion equations in biology. Computers Mathematics With Applications, 66(8): 1488–1497 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  17. Hereman, W. Application of a macsyma program for the painlev test to the Fitzhugh-Nagumo equation. Partially Intergrable Evolution Equations in Physics, 310: 585–586 (1990)

    Article  MathSciNet  Google Scholar 

  18. Hariharan, G. The homotopy analysis method applied to the Kolmogorov-Petrovskii-Piskunov (KPP) and fractional KPP equations. Journal of Mathematical Chemistry, 51(3): 992–1000 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  19. Huang, R., Jin, C.H., Mei, M., et al. Existence and stability of traveling waves for degenerate reaction-diffusion equation with time delay. Journal of Nonlinear science, 28: 1011–1042 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  20. Ichida, Y., Sakamoto, T.O. Radial symmetric stationary solutions for a MEMS type reaction-diffusion equation with spatially dependent nonlinearity. Japan Journal of Industrial and Applied Mathematics, 38: 297–322 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  21. Kolmogorov, A., Petrovskii, I., Piscunov, N. A study of the equation of diffusion with increase in the quantity of matter, and its application to a biological problem. Moscow University Bulletin of Mathematics, 1(6): 1–25 (1937)

    Google Scholar 

  22. Kametaka, Y. On the nonlinear diffusion equation of Kolmogorov-Petrovskii-Piskunov type. Osaka Journal of Mathematics, 13(1): 11–66 (1976)

    MathSciNet  MATH  Google Scholar 

  23. Kawahara, T., Tanaka, M. Interactions of traveling fronts: An exact solution of a nonlinear diffusion equation. Physics Letters A, 97(8): 311–314 (1983)

    Article  MathSciNet  Google Scholar 

  24. Li, J.B., Chen, G.R. On a class of singular nonlinear traveling wave equations. International Journal of Bifurcation & Chaos, 17(11): 4049–4065 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  25. Liu, J., Luo, H.Y., Mu, G., et al. New multi-soliton solutions for generalized Burgers-Huxley equation. Thermal Science, 17(5): 1486–1489 (2013)

    Article  Google Scholar 

  26. Li, H.Y., Guo, Y.C. New exact solutions to the Fitzhugh-Nagumo equation. Applied Mathematics and Computation, 180(2): 524–528 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  27. Murray, J.D. Mathematical Biology I,II. 3rd ed., Interdisciplinary Applied Mathematics. Springer-Verlag, New York, 2002

    Book  Google Scholar 

  28. Ma, W.X., Fuchssteiner, B. Explicit and exact solutions to a Kolmogorov-Petrovskii-Piskunov equation. International Journal of Non-linear Mechanics, 31(3): 329–338 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  29. Neubert, M.G., Caswell, H. Demography and dispersal: Calculation and sensitivity analysis of invasion speed for structured populations. Ecological Society of America, 81(6): 1613–1628 (2000)

    Google Scholar 

  30. Nemytskii, V., Stepanov, V. Qualitative theory of differential equations. Dover, New York, 1989

    MATH  Google Scholar 

  31. Pikulin, S.V. Traveling-wave solutions of the Kolmogorov-Petrovskii-Piskunov equation. Computational Mathematics and Mathematical Physics, 58(2): 230–237 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  32. Qin, C.Y., Tian, S.F., Wang, X.B., et al. Lie symmetry analysis, conservation laws and analytic solutions of the time fractional Kolmogorov-Petrovskii-Piskunov equation. Chinese Journal of Physics, 56(4): 1734–1742 (2018)

    Article  MathSciNet  Google Scholar 

  33. Rothe, F. Global solutions of reaction-diffusion systems. Lecture Notes in Mathematics, Vol.1072. Springer-Verlag, Berlin, 1984

    Book  MATH  Google Scholar 

  34. Smoller, J. Shock waves and reaction-diffusion equations, 2nd ed. Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], Vol.258. Springer-Verlag, New York, 1994

    Book  MATH  Google Scholar 

  35. Shapovalov, A.V., Trifonov, A.Y. Adomyan decomposition method for a two-component nonlocal reaction-diffusion model of the fisher-Kolmogorov-Petrovskii-Piskunov type. Russian Physics Journal, 62(5): 835–847 (2019)

    Article  Google Scholar 

  36. Song, L., Wang, W.G. Approximate solutions of nonlinear fractional Kolmogorov-Petrovskii-Piskunov equations using an enhanced algorithm of the generalized two-Dimensional differential transform method. Communications in Theoretical Physics, 58(2): 182–188 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  37. Saravanan, A., Magesh, N. A comparison between the reduced differential transform method and the Adomian decomposition method for the Newell-Whitehead-Segel equation. Journal of the Egyptian Mathematical Society, 21(3): 259–265 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  38. Tran, N., Au, V.V., Zhou, Y., et al. On a final value problem for fractional reaction-diffusion equation with Riemann-Liouville fractional derivative. Mathematical Methods in the Applied Sciences, 43(6): 3068–3098 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  39. Veeresha, P., Prakasha, D.G., Baleanu. D. An efficient numerical technique for the nonlinear fractional Kolmogorov-Petrovskii-Piskunov equation. Mathematics, 7: 7030265 (2019)

    Article  Google Scholar 

  40. Wang, D,S., Li, H.B. Single and multi-solitary wave solutions to a class of nonlinear evolution equations. Journal of Mathematical Analysis and Applications, 343(1): 273–298 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  41. Wang, K.F., Wang, W.D. Propagation of HBV with spatial dependence. Mathematical Bioences, 210(1): 78–95 (2007)

    MathSciNet  MATH  Google Scholar 

  42. Wang, W., Ma, W.B., Feng, Z.S. Dynamics of reaction-diffusion equations for modeling CD4 + T cells decline with general infection mechanism and distinct dispersal rates. Nonlinear Analysis Real World Applications, 51: 102976 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  43. Xu, R., Ma, Z.E. Global stability of a SIR epidemic model with nonlinear incidence rate and time delay. Nonlinear Analysis-real World Applications, 10(5): 3175–3189 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  44. Ye, Q.X., Li, Z.Y., Wang, M.X., et al. Introduction of reaction diffusion equation. Science Press, Beijing, 2011 (in Chinese)

    Google Scholar 

  45. Zhang, W,G., Chang, Q.S., Jiang, B.G. Explicit exact solitary-wave solutions for compound KdV-type and compound KdV-Burgers-type equations with nonlinear terms of any order. Chaos Solitons & Fractals, 13(2): 311–319 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  46. Zhang, W,G., Chang, Q.S., Fan, E.G. Methods of judging shape of solitary wave and solution formulae for some evolution equations with nonlinear terms of high order. Journal of Mathematical Analysis and Applications, 287(1): 1–18 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  47. Zhang, Z.F. Qualitative theory of differential equations. Translations of Mathematical Monographs, Vol.101. American Mathematical Society, 1992

  48. Zhang, G.G., Xiao, A.G. Exact and numerical stability analysis of reaction-diffusion equations with distributed delays. Frontiers of Mathematics in China, 11(1): 189–205 (2016)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. College of Science, University of Shanghai for Science and Technology, Shanghai, 200093, China

    Wei-guo Zhang, Xie-kui Hu, Xing-qian Ling & Wen-xia Li

Authors
  1. Wei-guo Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xie-kui Hu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Xing-qian Ling
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Wen-xia Li
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Wei-guo Zhang.

Additional information

This paper is supported by the National Natural Science Foundation of China (No. 11471215).

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhang, Wg., Hu, Xk., Ling, Xq. et al. Approximate Analytical Solution of the Generalized Kolmogorov-Petrovsky-Piskunov Equation with Cubic Nonlinearity. Acta Math. Appl. Sin. Engl. Ser. 39, 424–449 (2023). https://doi.org/10.1007/s10255-023-1054-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10255-023-1054-7

Keywords

2000 MR Subject Classification

Search

Navigation