Skip to main content
SpringerLink
Log in

Non-monotonous sequential subgradient projection algorithm for convex feasibility problem

  • Published:
Acta Mathematicae Applicatae Sinica, English Series Aims and scope Submit manuscript

Abstract

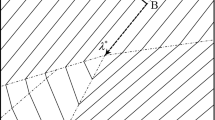
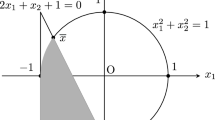
The existing methods of projection for solving convex feasibility problem may lead to slow convergence when the sequences enter some narrow“corridor” between two or more convex sets. In this paper, we apply a technique that may interrupt the monotonity of the constructed sequence to the sequential subgradient projection algorithm to construct a non-monotonous sequential subgradient projection algorithm for solving convex feasibility problem, which can leave such corridor by taking a big step at different steps during the iteration. Under some suitable conditions, the convergence is proved.We also compare the numerical performance of the proposed algorithm with that of the monotonous algorithm by numerical experiments.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Bauschke, H.H., Borwein, J.M. On projection algorithms for solving convex feasibility problems. SIAM Review, 38: 367–426 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  2. Boyd, S., EI Ghaoui, L., Feron, E., Balakrishnan, V. Linear Matrix Inequalities in System and Control Theory, Society for Industrial and Applied Mathematics (SIAM), Philadlphia, PA, USA, 1994

    Book  MATH  Google Scholar 

  3. Combettes, P.L. The foundations of set-theoretic estimation. Proceedings of the IEEE, 81: 182–208 (1993)

    Article  Google Scholar 

  4. Combettes, P.L. The convex feasibility problem in image recovery. Advances in Imaging and Electron Physics, 95: 155–270 (1996)

    Article  Google Scholar 

  5. Combettes, P.L. Convex set theoretic image recovery by extrapolated iterations of parallel subgradient projections. IEEE Transactions on Image Processing, 6: 493–506 (1997)

    Article  Google Scholar 

  6. Censor, Y., Altschuler, M.D., Powlis, W.D. On the use of Cimmino’s simultaneous projections method for computing a solution of the inverse problem in radiation therapy treatment planning. Inverse Problems, 4: 607–623 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  7. Censor, Y. Parallel application of block iterative methods in medical imaging and radiation therapy. Mathematical Programming, 42: 307–325 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  8. Censor, Y., Lent, A. Cyclic subgradient projections. Mathematical Programming, 24: 233–235 (1982)

    Article  MathSciNet  MATH  Google Scholar 

  9. Chinneck, J.W. The constraint consensus method for finding approximately feasible points in nonlinear programs. INFORMS Journal on Computing, 16: 255–265 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  10. Crombez, G. Non-monotoneous parallel iteration for solving convex feasibility problems. Kybernetika, 39: 547–560 (2003)

    MathSciNet  MATH  Google Scholar 

  11. Deutsch, F. The method of alternating orthogonal projections, Approximation Theory, Spline Functions and Applications. Kluwer Academic Publishers, Dordrecht, 1992, 105–121

    Book  MATH  Google Scholar 

  12. Dang Y.Z., Gao Y. Incomplete projection algorithm for solving a system of convex inequalities in a produce space. Journal of University of Shanghai for Science and Technology, 34(4): 56–61 (2012)

    Google Scholar 

  13. Eremin, I.I. On systems of inequalities with convex functions in the left sides. Transactions of the American Mathematical Society, 88: 67–83 (1970)

    MATH  Google Scholar 

  14. Eremin, I.I. Fejér mappings and convex programming. Siberian Mathematical Journal, 10: 762–772 (1969)

    Article  MathSciNet  MATH  Google Scholar 

  15. Gao, Y. Determining the viability for a affine nonlinear control system. Journal of Control Theory & Applications, 29: 654–656 (2009)

    Google Scholar 

  16. Herman, G.T. Image Reconstruction From Projection: The Fundamentals of Computerized Tomography. Academic Press, New York, 1980

    MATH  Google Scholar 

  17. Levi, A., Stark, H. Restoration from phase and magnitude by generalized projections, Image recovery: Theory and application. Academic Press, New York, 1987, 227–320

    Google Scholar 

  18. Marks, L.D., Sinkler, W., Landree, E. A feasible set approach to the crystallographic phase problem. Acta Crystallographica, A55: 601–612 (1999)

    Article  Google Scholar 

  19. Qu S. J., Goh M. and Ji Y., A new algorithm for linearly constrained convex vector optimization with a supply chain network risk application. Eur. J. Oper. Res., 247, 359–365(2015)

    Article  MathSciNet  Google Scholar 

  20. Ji Y., MarkGoh, Proximal point algorithms for multicriterla DC programming with applications to portfolio optimization, J. oPTIM. tHEORY, aPP. 169(1), 280–289(2016)

    Google Scholar 

  21. Rockafellar, R.T. Convex Analysis. Princeton Press, New Jersey, 1970

    Book  MATH  Google Scholar 

  22. Santos, L.T. A parallel subgradient projections method for the convex feasibility problem. Journal of Computational and Applied Mathematics, 18: 307–320 (1987)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Management, University of Shanghai for Science and Technology, Shanghai, 200093, China

    Ya-zheng Dang & Yan Gao

  2. School of Mathematics and Information Science, Henan Polytechnic University, Jiaozuo, 454000, China

    Jun-ling Sun

Authors
  1. Ya-zheng Dang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jun-ling Sun
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Yan Gao
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yan Gao.

Additional information

Supported by the National Science Foundation of China (No. 11171221), Natural Science Foundation of Shanghai (14ZR1429200), Innovation Program of Shanghai Municipal Education Commission (15ZZ074), Henan Province fundation frontier projec (No. 162300410226) Key Scientific research projectins of Henan Province(NO. 17b120001).

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Dang, Yz., Sun, Jl. & Gao, Y. Non-monotonous sequential subgradient projection algorithm for convex feasibility problem. Acta Math. Appl. Sin. Engl. Ser. 32, 1101–1110 (2016). https://doi.org/10.1007/s10255-016-0630-5

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10255-016-0630-5

Keywords

2000 MR Subject Classification

Search

Navigation