Skip to main content
SpringerLink
Log in

Four forbidden subgraph pairs for hamiltonicity of 3-connected graphs

  • Published:
Acta Mathematicae Applicatae Sinica, English Series Aims and scope Submit manuscript

Abstract

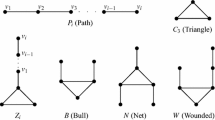
For non-negative integers i, j and k, we denote the generalized net as N i,j,k , which is a triangle with disjoint paths of length i, j and k, attached to distinct vertices of the triangle. In this paper, we prove that every 3-connected {K 1,3,N 8−i,i,1}-free graph is hamiltonian, where 1 ≤ i ≤ 4.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Catlin, P.A. A reduction methods to find spanning eulerian subgraphs. J. Graph Theory, 12: 29–44 (1988)

    Article  MathSciNet  MATH  Google Scholar 

  2. Chen, Z. Reduction of graphs and spanning eulerian subgraphs, Dissertation for Ph.D, Wayne State University, 1991

    Google Scholar 

  3. Diestel, R. Graph Theory, 3rd ed. Springer, 2005

    MATH  Google Scholar 

  4. Hu, Z., Lin, H. Two forbidden subgraph pairs for hamiltonicity of 3-connected graph. Graphs and Combinatorics, 29: 1755–1775 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  5. Lin, H., Hu, Z. Every 3-connected K 1,3,N 3,3,3-free graph is hamiltonian. Science China Mathematics, 56: 1585–1595 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  6. Lin, H. Forbidden subgraphs and hamiltonicity. Dissertation for Ph.D, The school of Mathematics and Statistics, Central China Normal University, 2012

    Google Scholar 

  7. Ryjácek, Z. On a closure concept in claw-free graphs. J. Combin. Theory Ser. B, 70: 217–224 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  8. Shao, Y. Claw-free graphs and line graphs. Dissertation for Ph.D, Department of Mathematics, West Virginia University, 2005

    Google Scholar 

  9. Xiong, W., Lai H., Ma X., Wang K., Zhang M. Hamilton cycles in 3-connected claw-free and net-free graphs. Discrete Math., 313: 784–795 (2013)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Mathematics and Quantitative Economics, Shandong University of Finance and Economics, Jinan, 250014, China

    Hou-yuan Lin

  2. Faculty of Mathematics and Statistics, Central China Normal University, Wuhan, 430079, China

    Zhi-quan Hu

Authors
  1. Hou-yuan Lin
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Zhi-quan Hu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Hou-yuan Lin.

Additional information

Supported by the National Natural Science Foundation of China (No. 11371162 and No. 11271149), A project of Shandong Province Higher Educational Science and Technology Program (No. J15LI52), Science and Technology Development Project of Shandong Province (No. 2014GGX101033).

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Lin, Hy., Hu, Zq. Four forbidden subgraph pairs for hamiltonicity of 3-connected graphs. Acta Math. Appl. Sin. Engl. Ser. 32, 469–476 (2016). https://doi.org/10.1007/s10255-016-0573-x

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10255-016-0573-x

Keywords

2000 MR Subject Classification

Search

Navigation