Skip to main content
SpringerLink
Log in

A closed form solution to one dimensional robin boundary problems

  • Published:
Acta Mathematicae Applicatae Sinica, English Series Aims and scope Submit manuscript

Abstract

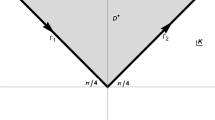
Many cellular and subcellular biological processes can be described in terms of diffusing and chemically reacting species (e.g. enzymes). In this paper, we will use reflected and absorbed Brownian motion and stochastic differential equations to construct a closed form solution to one dimensional Robin boundary problems. Meanwhile, we will give a reasonable explanation to the closed form solution from a stochastic point of view. Finally, we will extend the problem to Robin boundary problem with two boundary conditions and give a specific solution by resorting to a stopping time.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Andrews, S.S., Bray, D. Stochastic simulation of chemical reactions with spatial resolution and single molecule detail. Physical Biology, 1: 137–151 (2004)

    Article  Google Scholar 

  2. Erban, R., Chapman, S.J. Reactive boundary conditions for stochastic simulations of reaction diffusion processes. Physical Biology, 4: 16–28 (2007)

    Article  Google Scholar 

  3. Hattne, J., Fagne, D., Elf, J. Stochastic reaction-diffusion simulation with MesoRD. Bioinformatics, 21(12): 2923–2924 (2005)

    Article  Google Scholar 

  4. Isaacson, S.A., Peskin, C.S. Incorporating diffusion in complex geometries into stochastic chemical kinetics simulations. SIAM Journal on Scientific Computing, 28(1): 47–74 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  5. Karatzas, I., Shreve, S.E. Brownian Motion and Stochastic Calculus. Springer-Verlag, 1988

  6. Lyons, T.J., Zheng, W.A. On conditional diffusion processes. In: Proceedings of the Royal Society of Edinburgh, Section A. Mathematics 115: 243–255 (1990)

    Article  MathSciNet  MATH  Google Scholar 

  7. Qian, Z.M., Zheng, W.A. Sharp bounds for transition probability densities of a class of diffusions. Comptes Rendus Mathematique, 335: 953–957 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  8. Revuz, D., Yor, M. Continuous Martingales and Brownian Motion. Springer-Verlag, 1991

  9. Stundzia, A., Lumsden, C. Stochastic simulation of coupled reaction-diffusion processes. Journal of Computational Physics, 127: 196–207 (1996)

    Article  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Physics Department, East China Normal University, 200062, Shanghai, China

    Chang-li Yang

  2. School of Finance and Statistics, East China Normal University, 200062, Shanghai, China

    Ai-lin Zhu

Authors
  1. Chang-li Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ai-lin Zhu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ai-lin Zhu.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Yang, Cl., Zhu, Al. A closed form solution to one dimensional robin boundary problems. Acta Math. Appl. Sin. Engl. Ser. 28, 549–556 (2012). https://doi.org/10.1007/s10255-012-0156-4

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10255-012-0156-4

Keywords

2000 MR Subject Classification

Search

Navigation