Bifurcations of resonant solutions and chaos in physical pendulum equation with suspension axis vibrations

Abstract

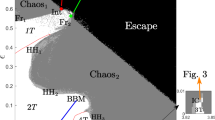
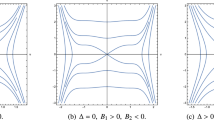
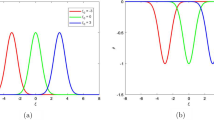
This paper is a continuation of “Complex Dynamics in Physical Pendulum Equation with Suspension Axis Vibrations”[1]. In this paper, we investigate the existence and the bifurcations of resonant solution for ω ₀: ω: Ω ≈ 1: 1: n,1: 2: n,1: 3: n,2: 1: n and 3: 1: n by using second-order averaging method, give a criterion for the existence of resonant solution for ω ₀: ω: Ω ≈ 1: m: n by using Melnikov’s method and verify the theoretical analysis by numerical simulations. By numerical simulation, we expose some other interesting dynamical behaviors including the entire invariant torus region, the cascade of invariant torus behaviors, the entire chaos region without periodic windows, chaotic region with complex periodic windows, the entire period-one orbits region; the jumping behaviors including invariant torus behaviors converting to period-one orbits, from chaos to invariant torus behaviors or from invariant torus behaviors to chaos, from period-one to chaos, from invariant torus behaviors to another invariant torus behaviors; the interior crisis; and the different nice invariant torus attractors and chaotic attractors. The numerical results show the difference of dynamical behaviors for the physical pendulum equation with suspension axis vibrations between the cases under the three frequencies resonant condition and under the periodic/quasi-periodic perturbations. It exhibits many invariant torus behaviors under the resonant conditions. We find a lot of chaotic behaviors which are different from those under the periodic/quasi-periodic perturbations. However, we did not find the cascades of period-doubling bifurcation.