Abstract
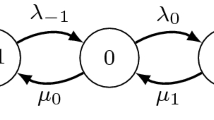
The state 0 of a birth and death process with state space E = {0, 1, 2, … } is a barrier which can be classified into four kinds: reflection, absorption, leaping reflection, quasi-leaping reflection. For the first, second and fourth barriers, the characteristic numbers of different forms have been introduced. In this paper unified characteristic numbers for birth and death processes with barriers were introduced, the related equations were solved and the solutions were expressed by unified characteristic numbers. This paper concerns work solving probability construction problem of birth and death processes with leaping reflection barrier and quasi-leaping reflection barrier.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Feller, W. The Birth and Death processes as diffusion processes. J. Math Pures Appl., 9: 301–345 (1959)
Gao, P. The birth and death processes with zero as their absorbing barrieer. Acta Math. Appl. Sinica., 2(4): 292–303 (1985)
Wang, Z.K. Classification of all birth and death processes. Science report of Universities. Phys.-Math. Science, 4: 19–25 1958 (in Russion)
Wang, Z.K., Yang, X.Q. The Birth and Death Process and Markov Chains, 2nd Ed. Science Press, Beijing, 2005
Wang, Z.K., Yang, X.Q. The Birth and Death processes and Markov chains. Springer-Verlag, Berlin, 1992
Wang, Z.K. The construction theory of birth and death processes. Chin. Math. Adv., 5: 137–187 (1962)
Wang, Z.K., Yang, X.Q. The construction for stopping birth and death processes. Acta. Math. Sinica., 21: 61–71 (1978)
Yang, C.Q. A class of birth and death processes. Acta. Math., 15: 9–31 (1965)
Yang, C.Q. Notes on the construction theroy of birth and death processes. Acta. Math. Sinica., 15: 173–187 (1965) (in Chinese)
Yang, X.Q. The construction Theory of Denumerable Markov Processes. Hunan Science and Technology Press, Changsha, China, 1986 (in Chinese)
Yang, X.Q. The Construction Theory of denumerable Markov Process. Wiley and Sons Lmt, Chichester, UK, 1990
Yang, X.Q., Wang, Z.Q. Probability-Analysis method in Construction theory for stopping birth and death proecesses. J. Nankai. Univ. (Natural Sci.), China, 3: 1–32 (1979)
Yang, X.Q. Distributions of lifetime after explosion for birth and death processes. Sci. China Ser. A-Math, 41(7): 694–699 (1998)
Yang, X.Q. Some properties of repeated hits after first explosion for birth and death processes. Sci China Ser A-Math, 42(5): 471–477 (1999)
Yang, X.Q., Liu, S.Y. Joint distributions of first hitting time and first hitting location after explosion for birth and death processes. Sci. China (Series A), 43(1): 1014–1018 (2000)
Yang, X.Q., Liu, S.Y. Decomposition and embedment of trajectory after explosion for a birth and death processes. Sci China (Series A), 45(1): 1100–1105 (2002)
Zhu, Q.X., Shu, X.B. The characteristic numbers and Their Probability Meaning of two Kinds of birth and death Processes. J. Ann. Math Chinese Univ. Ser. A, 21(3): 311–320 (2006)
Author information
Authors and Affiliations
Corresponding author
Additional information
Supported by the National Natural Science Foundation of China (Grant No. 10571051 and 10871064) and by the Specialized Research Fund for the Doctoral Program of Higher Education of China (No. 20040542006) and by the Key Labor. of Coput.Stoch.Math.Univ. of Hunan (No. 09K026).
Rights and permissions
About this article
Cite this article
Xiang-qun, Y., He-song, W. Unified characteristic numbers and solutions of equations for birth and death processes with barriers. Acta Math. Appl. Sin. Engl. Ser. 26, 443–454 (2010). https://doi.org/10.1007/s10255-010-0009-y
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10255-010-0009-y
Keywords
- birth and death process with barrier
- reflection and absorption
- leaping reflection and quasi-reflection
- characteristic numbers
- solutions of equations