Abstract
We show that abelian surfaces (and consequently curves of genus 2) over totally real fields are potentially modular. As a consequence, we obtain the expected meromorphic continuation and functional equations of their Hasse–Weil zeta functions. We furthermore show the modularity of infinitely many abelian surfaces \(A\) over \({\mathbf {Q}}\) with \(\operatorname{End}_{ {\mathbf {C}}}A={\mathbf {Z}}\). We also deduce modularity and potential modularity results for genus one curves over (not necessarily CM) quadratic extensions of totally real fields.
Article PDF
Similar content being viewed by others
Avoid common mistakes on your manuscript.
References
J. Arthur and L. Clozel, Simple algebras, base change, and the advanced theory of the trace formula, Annals of Mathematics Studies, vol. 120, Princeton University Press, Princeton, 1989.
P. Allen, F. Calegari, A. Caraiani, T. Gee, D. Helm, B. Le Hung, J. Newton, P. Scholze, R. Taylor and J. Thorne, Potential automorphy over CM fields, preprint, 2018.
A. Ash, P. E. Gunnells and M. McConnell, Cohomology with twisted one-dimensional coefficients for congruence subgroups of \({\mathrm {SL}}_{4}(\Bbb {Z})\) and Galois representations, J. Algebra, 553 (2020), 211–247.
F. Andreatta, A. Iovita and V. Pilloni, \(p\)-adic families of Siegel modular cuspforms, Ann. Math. (2), 181 (2015), 623–697.
P. B. Allen, Deformations of polarized automorphic Galois representations and adjoint Selmer groups, Duke Math. J., 165 (2016), 2407–2460.
A. Ash, D. Mumford, M. Rapoport and Y.-S. Tai, Smooth compactifications of locally symmetric varieties, 2nd ed., Cambridge Mathematical Library, Cambridge University Press, Cambridge, 2010, With the collaboration of Peter Scholze.
J. Arthur, Automorphic representations of \({\mathrm{ GSp}(4)}\), Contributions to automorphic forms, geometry, and number theory, pp. 65–81, Johns Hopkins Univ. Press, Baltimore, 2004.
J. Arthur, The endoscopic classification of representations, American Mathematical Society Colloquium Publications, vol. 61, Am. Math. Soc., Providence, 2013, Orthogonal and symplectic groups.
A. Ash and G. Stevens, \(p\)-adic deformations of arithmetic cohomology, preprint, 2008.
E. Artin and J. Tate, Class field theory, AMS Chelsea Publishing, Providence, 2009, Reprinted with corrections from the 1967 original.
G. Böckle, Demuškin groups with group actions and applications to deformations of Galois representations, Compos. Math., 121 (2000), 109–154.
H. F. Baker, A Locus with 25920 Linear Self-Transformations, Cambridge Tracts in Mathematics and Mathematical Physics, vol. 39, Cambridge University Press/The Macmillan Company, Cambridge/New York, 1946.
S. Balaji, G-valued potentially semi-stable deformation rings, ProQuest LLC, Ann Arbor, MI, 2012, Thesis (Ph.D.)–The University of Chicago.
J. Bellaïche and G. Chenevier, The sign of Galois representations attached to automorphic forms for unitary groups, Compos. Math., 147 (2011), 1337–1352.
C. Breuil, B. Conrad, F. Diamond and R. Taylor, On the modularity of elliptic curves over
 : wild 3-adic exercises, J. Am. Math. Soc., 14 (2001), 843–939 (electronic).
: wild 3-adic exercises, J. Am. Math. Soc., 14 (2001), 843–939 (electronic).
G. Boxer, F. Calegari, T. Gee and V. Pilloni, Auxiliary magma files, 2021, https://github.com/fcale75/abeliansurfacesmagmafiles.
W. Bosma, J. Cannon and C. Playoust, The Magma algebra system. I. The user language, J. Symb. Comput., 24 (1997), 235–265, Computational algebra and number theory (London, 1993)
T. Berger, L. Dembélé, A. Pacetti and M. H. Şengün, Theta lifts of Bianchi modular forms and applications to paramodularity, J. Lond. Math. Soc. (2), 92 (2015), 353–370.
S. Baba and H. Granath, Genus 2 curves with quaternionic multiplication, Can. J. Math., 60 (2008), 734–757.
K. Buzzard and T. Gee, The conjectural connections between automorphic representations and Galois representations, in Automorphic forms and Galois representations. Vol. 1, London Math. Soc. Lecture Note Ser., vol. 414, pp. 135–187, Cambridge University Press, Cambridge, 2014.
R. Bellovin and T. Gee, \(G\)-valued local deformation rings and global lifts, Algebra Number Theory, 13 (2019), 333–378.
D. Blasius, M. Harris and D. Ramakrishnan, Coherent cohomology, limits of discrete series, and Galois conjugation, Duke Math. J., 73 (1994), 647–685.
G. Böckle and A.-K. Juschka, Irreducibility of versal deformation rings in the \((p,p)\)-case for 2-dimensional representations, J. Algebra, 444 (2015), 81–123.
A. Brumer and K. Kramer, Paramodular abelian varieties of odd conductor, Trans. Am. Math. Soc., 366 (2014), 2463–2516.
A. Brumer and K. Kramer, Corrigendum to “Paramodular abelian varieties of odd conductor”, Trans. Am. Math. Soc., 372 (2019), 2251–2254.
T. Berger and K. Klosin, Deformations of Saito-Kurokawa type and the paramodular conjecture, Am. J. Math., 142 (2020), 1821–1875, With and appendix by Chris Poor, Jerry Shurman, and David S. Yuen.
C. Birkenhake and H. Lange, Complex abelian varieties, 2nd ed., Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 302, Springer, Berlin, 2004.
D. Blasius, Hilbert modular forms and the Ramanujan conjecture, in Noncommutative geometry and number theory, Aspects Math., vol. E37, pp. 35–56, Vieweg, Wiesbaden, 2006.
T. Barnet-Lamb, T. Gee and D. Geraghty, Congruences between Hilbert modular forms: constructing ordinary lifts, II, Math. Res. Lett., 20 (2013), 67–72.
T. Barnet-Lamb, T. Gee, D. Geraghty and R. Taylor, Local-global compatibility for \(l=p\), II, Ann. Sci. Éc. Norm. Supér. (4), 47 (2014), 165–179.
T. Barnet-Lamb, T. Gee, D. Geraghty and R. Taylor, Potential automorphy and change of weight, Ann. Math. (2), 179 (2014), 501–609.
T. Barnet-Lamb, D. Geraghty, M. Harris and R. Taylor, A family of Calabi-Yau varieties and potential automorphy II, Publ. Res. Inst. Math. Sci., 47 (2011), 29–98.
N. Bruin and B. Nasserden, Arithmetic aspects of the Burkhardt quartic threefold, J. Lond. Math. Soc. (2), 98 (2018), 536–556.
M. Bolognesi, On Weddle surfaces and their moduli, Adv. Geom., 7 (2007), 113–144.
G. Boxer, Torsion in the coherent cohomology of Shimura varieties and Galois representations, preprint, 2015.
A. Brumer, A. Pacetti, C. Poor, G. Tornaría, J. Voight and D. S. Yuen, On the paramodularity of typical abelian surfaces, Algebra Number Theory, 13 (2019), 1145–1195.
S. Bijakowski, V. Pilloni and B. Stroh, Classicité de formes modulaires surconvergentes, Ann. Math. (2), 183 (2016), 975–1014.
J. Breeding II, C. Poor and D. S. Yuen, Computations of spaces of paramodular forms of general level, J. Korean Math. Soc., 53 (2016), 645–689.
R. Brasca and G. Rosso, Eigenvarieties for non-cuspidal modular forms over certain PEL Shimura varieties, 2016.
R. Brauer, On Artin’s \(L\)-series with general group characters, Ann. Math. (2), 48 (1947), 502–514.
K. Buzzard and R. Taylor, Companion forms and weight one forms, Ann. Math. (2), 149 (1999), 905–919.
H. Burkhardt, Untersuchungen aus dem Gebiete der hyperelliptischen Modulfunctionen, Math. Ann., 38 (1891), 161–224.
K. Buzzard, Analytic continuation of overconvergent eigenforms, J. Am. Math. Soc., 16 (2003), 29–55.
B. Cais, On the \(U_{p}\) operator in characteristic \(p\), Math. Res. Lett., 21 (2014), 255–260.
F. Calegari, Even Galois Representations and the Fontaine-Mazur conjecture II, J. Am. Math. Soc., 25 (2012), 533–554.
F. Calegari, Non-minimal modularity lifting in weight one, J. Reine Angew. Math., 740 (2018), 41–62.
A. Caraiani, Local-global compatibility and the action of monodromy on nearby cycles, Duke Math. J., 161 (2012), 2311–2413.
A. Caraiani, Monodromy and local-global compatibility for \(l=p\), Algebra Number Theory, 8 (2014), 1597–1646.
W. Casselman, Introduction to admissible representations of \(p\)-adic groups, Available at https://www.math.ubc.ca/~cass/research/publications.html.
F. Calegari and S. Chidambaram, Rationality of twists of the Siegel modular variety of genus 2 and level 3, 2020, https://arxiv.org/abs/2009.00194.
F. Calegari, S. Chidambaram and A. Ghitza, Some modular abelian surfaces, Math. Comput., 89 (2020), 387–394.
J. H. Conway, R. T. Curtis, S. P. Norton, R. A. Parker and R. A. Wilson, Atlas of finite groups, Oxford University Press, Eynsham, 1985, Maximal subgroups and ordinary characters for simple groups, With computational assistance from J. G. Thackray
B. Conrad, F. Diamond and R. Taylor, Modularity of certain potentially Barsotti-Tate Galois representations, J. Am. Math. Soc., 12 (1999), 521–567.
F. Calegari and T. Gee, Irreducibility of automorphic Galois representations of \(GL(n)\), \(n\) at most 5, Ann. Inst. Fourier (Grenoble), 63 (2013), 1881–1912.
F. Calegari and D. Geraghty, Modularity lifting beyond the Taylor–Wiles method, Invent. Math., 211 (2018), 297–433.
F. Calegari and D. Geraghty, Minimal modularity lifting for nonregular symplectic representations, Duke Math. J., 169 (2020), 801–896, With an appendix by Calegari, Geraghty and Michael Harris.
G. Chenevier, Familles \(p\)-adiques de formes automorphes pour \({\mathrm{ GL}}_{n}\), J. Reine Angew. Math., 570 (2004), 143–217.
W. C. Chi, On the \(l\)-adic representations attached to some absolutely simple abelian varieties of type \({\mathrm{ II}}\), J. Fac. Sci., Univ. Tokyo, Sect. 1A, Math., 37 (1990), 467–484.
W. C. Chi, \(l\)-adic and \(\lambda \)-adic representations associated to abelian varieties defined over number fields, Am. J. Math., 114 (1992), 315–353.
L. Clozel, M. Harris and R. Taylor, Automorphy for some \(l\)-adic lifts of automorphic mod \(l\) Galois representations, Publ. Math. IHES, 108 (2008), 1–181.
P.-H. Chaudouard and G. Laumon, Le lemme fondamental pondéré. I. Constructions géométriques, Compos. Math., 146 (2010), 1416–1506.
L. Clozel, Motifs et formes automorphes: applications du principe de fonctorialité, in Automorphic forms, Shimura varieties and \(L\)-functions, Vol. I, Perspect. Math., vol. 10, Ann Arbor, MI, 1988, pp. 77–159, Academic Press, Boston, 1990.
A. B. Coble, An invariant condition for certain automorphic algebraic forms, Am. J. Math., 28 (1906), 333–366.
R. F. Coleman, P-adic Banach spaces and families of modular forms, Invent. Math., 127 (1997), 417–479.
J. E. Cremona, Hyperbolic tessellations, modular symbols, and elliptic curves over complex quadratic fields, Compos. Math., 51 (1984), 275–324.
J. E. Cremona, Abelian varieties with extra twist, cusp forms, and elliptic curves over imaginary quadratic fields, J. Lond. Math. Soc. (2), 45 (1992), 404–416.
H. Darmon, F. Diamond and R. Taylor, Fermat’s last theorem, in Elliptic curves, modular forms & Fermat’s last theorem, Hong Kong, 1993, pp. 2–140, Int. Press, Cambridge, 1997.
P. Deligne, Les constantes des équations fonctionnelles des fonctions \(L\), in Modular functions of one variable, II, Lecture Notes in Math., vol. 349, Proc. Internat. Summer School, Univ. Antwerp, Antwerp, 1972, pp. 501–597, Springer, Berlin, 1973.
P. Deligne, Variétés de Shimura: interprétation modulaire, et techniques de construction de modèles canoniques, in Automorphic forms, representations and \(L\)-functions, Part 2, Proc. Sympos. Pure Math., vol. XXXIII, Proc. Sympos. Pure Math., Oregon State Univ., Corvallis, Ore, 1977, pp. 247–289, Am. Math. Soc., Providence, 1979.
F. Diamond, The Taylor–Wiles construction and multiplicity one, Invent. Math., 128 (1997), 379–391.
A. J. de Jong, The moduli spaces of principally polarized abelian varieties with \(\Gamma _{0}(p)\)-level structure, J. Algebraic Geom., 2 (1993), 667–688.
W. Duke and E. Kowalski, A problem of Linnik for elliptic curves and mean-value estimates for automorphic representations, Invent. Math., 139 (2000), 1–39, With an appendix by Dinakar Ramakrishnan.
L. Dembélé and A. Kumar, Examples of abelian surfaces with everywhere good reduction, Math. Ann., 364 (2016), 1365–1392.
F. Diamond and P. L. Kassaei, Minimal weights of Hilbert modular forms in characteristic \(p\), Compos. Math., 153 (2017), 1769–1778.
I. Dolgachev and D. Lehavi, On isogenous principally polarized abelian surfaces, in Curves and abelian varieties, Contemp. Math., vol. 465, pp. 51–69, Am. Math. Soc., Providence, 2008.
P. Deligne and M. Rapoport, Les schémas de modules de courbes elliptiques, in Modular functions of one variable, II, Lecture Notes in Math., vol. 349, Proc. Internat. Summer School, Univ. Antwerp, Antwerp, 1972, pp. 143–316, Springer, Berlin, 1973.
B. Edixhoven, The weight in Serre’s conjectures on modular forms, Invent. Math., 109 (1992), 563–594.
M. Emerton and T. Gee, A geometric perspective on the Breuil-Mézard conjecture, J. Inst. Math. Jussieu, 13 (2014), 183–223.
J. S. Ellenberg, Serre’s conjecture over \(\Bbb {F}_{9}\), Ann. Math. (2), 161 (2005), 1111–1142.
M. Emerton, D. Reduzzi and L. Xiao, Unramifiedness of Galois representations arising from Hilbert modular surfaces, Forum Math. Sigma, 5, e29 (2017).
G. Faltings, Endlichkeitssätze für abelsche Varietäten über Zahlkörpern, Invent. Math., 73 (1983), 349–366.
L. Fargues, L’isomorphisme entre les tours de Lubin-Tate et de Drinfeld et applications cohomologiques, in L’isomorphisme entre les tours de Lubin-Tate et de Drinfeld, Progr. Math., vol. 262, pp. 1–325, Birkhäuser, Basel, 2008.
L. Fargues, La filtration de Harder-Narasimhan des schémas en groupes finis et plats, J. Reine Angew. Math., 645 (2010), 1–39.
L. Fargues, La filtration canonique des points de torsion des groupes \(p\)-divisibles, Ann. Sci. Éc. Norm. Supér. (4), 44 (2011), 905–961, With collaboration of Yichao Tian.
G. Faltings and C.-L. Chai, Degeneration of abelian varieties, Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)], vol. 22, Springer, Berlin, 1990, With an appendix by David Mumford.
F. Fité, K. S. Kedlaya, V. Rotger and A. V. Sutherland, Sato-Tate distributions and Galois endomorphism modules in genus 2, Compos. Math., 148 (2012), 1390–1442.
J.-M. Fontaine, Représentations \(l\)-adiques potentiellement semi-stables, Astérisque, 223 (1994), 321–347, Périodes \(p\)-adiques (Bures-sur-Yvette, 1988).
N. Fakhruddin and V. Pilloni, Hecke operators and the coherent cohomology of Shimura varieties, J. Inst. Math. Jussieu (2021), 1–69.
E. Freitag, Siegelsche Modulfunktionen, Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 254, Springer, Berlin, 1983.
D. Geraghty, Modularity lifting theorems for ordinary Galois representations, Math. Ann., 373 (2019), 1341–1427.
T. Gee and D. Geraghty, Companion forms for unitary and symplectic groups, Duke Math. J., 161 (2012), 247–303.
T. Gee, F. Herzig, T. Liu and D. Savitt, Potentially crystalline lifts of certain prescribed types, Doc. Math., 22 (2017), 397–422.
R. Godement and H. Jacquet, Zeta functions of simple algebras, Lecture Notes in Mathematics, vol. 260, Springer, Berlin, 1972.
W. Goldring and J.-S. Koskivirta, Strata Hasse invariants, Hecke algebras and Galois representations, Invent. Math., 217 (2019), 887–984.
T. Gee and J. Newton, Patching and the completed homology of locally symmetric spaces, J. Inst. Math. Jussieu (2020), 1–64.
S. Gelbart, I. Piatetski-Shapiro and S. Rallis, Explicit constructions of automorphic \(L\)-functions, Lecture Notes in Mathematics, vol. 1254, Springer, Berlin, 1987.
B. H. Gross, A tameness criterion for Galois representations associated to modular forms (mod \(p\)), Duke Math. J., 61 (1990), 445–517.
B. H. Gross, On the Langlands correspondence for symplectic motives, Izv. Ross. Akad. Nauk Ser. Mat., 80 (2016), 49–64.
A. Grothendieck, M. Raynaud and D. S. Rim, Groupes de monodromie en géométrie algébrique. I, Lecture Notes in Mathematics, vol. 288, Springer, Berlin, 1972, Séminaire de Géométrie Algébrique du Bois-Marie 1967–1969 (SGA 7 I), Dirigé par A. Grothendieck. Avec la collaboration de Michèle Raynaud et Dock S. Rim.
A. Genestier and J. Tilouine, Systèmes de Taylor-Wiles pour \({\mathrm{GSp}}(4)\), Astérisque, 302 (2005), 177–290, Formes automorphes. II. Le cas du groupe \({\mathrm{GSp}}(4)\).
W. T. Gan and S. Takeda, The local Langlands conjecture for \({\mathrm {G}Sp}(4)\), Ann. Math. (2), 173 (2011), 1841–1882.
W. T. Gan and S. Takeda, Theta correspondences for \({\mathrm {GSp}}(4)\), Represent. Theory, 15 (2011), 670–718.
T. Gee and O. Taïbi, Arthur’s multiplicity formula for \({\bf GSp}_{4}\) and restriction to \({\bf Sp}_{4}\), J. Éc. Polytech. Math., 6 (2019), 469–535.
R. Hartshorne, Residues and duality, in Lecture notes of a seminar on the work of A. Grothendieck, given at Harvard 1963/64, Lecture Notes in Mathematics, vol. 20, Springer, Berlin, 1966, With an appendix by Pierre Deligne.
M. Harris, Automorphic forms and the cohomology of vector bundles on Shimura varieties, in Automorphic forms, Shimura varieties, and \(L\)-functions, Vol. II, Perspect. Math., vol. 11, Ann Arbor, MI, 1988, pp. 41–91, Academic Press, Boston, 1990.
M. Harris, Automorphic forms of \(\overline{\partial}\)-cohomology type as coherent cohomology classes, J. Differ. Geom., 32 (1990), 1–63.
E. Hecke, Eine neue Art von Zetafunktionen und ihre Beziehungen zur Verteilung der Primzahlen, Math. Z., 6 (1920), 11–51.
G. Henniart, Sur la fonctorialité, pour \(\mathrm{GL}(4)\), donnée par le carré extérieur, Mosc. Math. J., 9 (2009), 33–45, back matter.
H. Hida, \(p\)-adic automorphic forms on Shimura varieties, Springer Monographs in Mathematics, Springer, New York, 2004.
H. Hida, Irreducibility of the Igusa tower, Acta Math. Sin. Engl. Ser., 25 (2009), 1–20.
T. J. Haines, R. E. Kottwitz and A. Prasad, Iwahori-Hecke algebras, J. Ramanujan Math. Soc., 25 (2010), 113–145.
M. Harris, K.-W. Lan, R. Taylor and J. Thorne, On the rigid cohomology of certain Shimura varieties, Res. Math. Sci., 3 (2016), 37.
K. Hulek and G. K. Sankaran, The geometry of Siegel modular varieties, in Higher dimensional birational geometry, Adv. Stud. Pure Math., vol. 35, Kyoto, 1997, pp. 89–156, Math. Soc. Japan, Tokyo, 2002.
M. Harris and R. Taylor, The geometry and cohomology of some simple Shimura varieties, Annals of Mathematics Studies, vol. 151, Princeton University Press, Princeton, 2001, With an appendix by Vladimir G. Berkovich.
R. Huber, Étale cohomology of rigid analytic varieties and adic spaces, Aspects of Mathematics, vol. E30, Friedr. Vieweg & Sohn, Braunschweig, 1996.
B. Hunt, The geometry of some special arithmetic quotients, Lecture Notes in Mathematics, vol. 1637, Springer, Berlin, 1996.
M. Harris and S. Zucker, Boundary cohomology of Shimura varieties. III. Coherent cohomology on higher-rank boundary strata and applications to Hodge theory, Mém. Soc. Math. Fr. (N.S.) (2001) vi+116.
J. Igusa, On Siegel modular forms genus two. II, Am. J. Math., 86 (1964), 392–412.
J. Johnson-Leung and B. Roberts, Siegel modular forms of degree two attached to Hilbert modular forms, J. Number Theory, 132 (2012), 543–564.
N. Jochnowitz, Congruences between systems of eigenvalues of modular forms, Trans. Am. Math. Soc., 270 (1982), 269–285.
C. Johansson, On the Sato-Tate conjecture for non-generic abelian surfaces, Trans. Am. Math. Soc., 369 (2017), 6303–6325, With an appendix by Francesc Fité.
O. T. R. Jones, An analogue of the BGG resolution for locally analytic principal series, J. Number Theory, 131 (2011), 1616–1640.
H. Jacquet and J. A. Shalika, On Euler products and the classification of automorphic forms. II, Am. J. Math., 103 (1981), 777–815.
P. L. Kassaei, A gluing lemma and overconvergent modular forms, Duke Math. J., 132 (2006), 509–529.
P. L. Kassaei, Analytic continuation of overconvergent Hilbert modular forms, Astérisque, 382 (2016), 1–48.
G. Kempf, The Grothendieck–Cousin complex of an induced representation, Adv. Math., 29 (1978), 310–396.
H. H. Kim, Functoriality for the exterior square of \({\mathrm{ GL}}_{4}\) and the symmetric fourth of \({\mathrm{ GL}}_{2}\), J. Am. Math. Soc., 16 (2003), 139–183, With appendix 1 by Dinakar Ramakrishnan and appendix 2 by Kim and Peter Sarnak.
M. Kisin, Potentially semi-stable deformation rings, J. Am. Math. Soc., 21 (2008), 513–546.
M. Kisin, Moduli of finite flat group schemes, and modularity, Ann. Math. (2), 170 (2009), 1085–1180.
S. L. Kleiman, The standard conjectures, in Motives, Proc. Sympos. Pure Math., vol. 55, Seattle, WA, 1991, pp. 3–20, Am. Math. Soc., Providence, 1994.
R. E. Kottwitz, Points on some Shimura varieties over finite fields, J. Am. Math. Soc., 5 (1992), 373–444.
S. S. Kudla and M. Rapoport, Arithmetic Hirzebruch-Zagier cycles, J. Reine Angew. Math., 515 (1999), 155–244.
P. L. Kassaei, S. Sasaki and Y. Tian, Modularity lifting results in parallel weight one and applications to the Artin conjecture: the tamely ramified case, Forum Math. Sigma, 2, e18 (2014).
C. B. Khare and J. A. Thorne, Potential automorphy and the Leopoldt conjecture, Am. J. Math., 139 (2017), 1205–1273.
R. P. Langlands, Base change for \({\mathrm{ GL}}(2)\), Annals of Mathematics Studies, vol. 96, Princeton University Press/University of Tokyo Press, Princeton/Tokyo, 1980.
K.-W. Lan, Arithmetic compactifications of PEL-type Shimura varieties, London Mathematical Society Monographs Series, vol. 36, Princeton University Press, Princeton, 2013.
K.-W. Lan, Compactifications of PEL-type Shimura varieties in ramified characteristics, Forum Math. Sigma, 4, e1 (2016).
K.-W. Lan, Integral models of toroidal compactifications with projective cone decompositions, Int. Math. Res. Not., 11 (2017), 3237–3280.
G. Lombardo, C. Peters and M. Schütt, Abelian fourfolds of Weil type and certain K3 double planes, Rend. Semin. Mat. Univ. Politec. Torino, 71 (2013), 339–383.
B. Mazur, Deforming Galois representations, in Galois groups over \({\bf Q}\), Math. Sci. Res. Inst. Publ., vol. 16, Berkeley, CA, 1987, pp. 385–437, Springer, New York, 1989.
L. Moret-Bailly, Groupes de Picard et problèmes de Skolem II, Ann. Sci. Éc. Norm. Supér., 22 (1989), 181–194.
L. Moret-Bailly, Extensions de corps globaux à ramification et groupe de Galois donnés, C. R. Acad. Sci., Sér. 1 Math., 311 (1990), 273–276.
W. Messing, The crystals associated to Barsotti-Tate groups: with applications to abelian schemes, Lecture Notes in Mathematics, vol. 264, Springer, Berlin, 1972.
J. S. Milne, Points on Shimura varieties mod \(p\), in Automorphic forms, representations and \(L\)-functions, Part 2, Proc. Sympos. Pure Math., vol. XXXIII, Proc. Sympos. Pure Math., Oregon State Univ., Corvallis, Ore., 1977, pp. 165–184, Am. Math. Soc., Providence, 1979.
C. P. Mok, Galois representations attached to automorphic forms on \({\mathrm {GL}}_{2}\) over CM fields, Compos. Math., 150 (2014), 523–567.
D. R. Morrison, On \(K3\) surfaces with large Picard number, Invent. Math., 75 (1984), 105–121.
D. R. Morrison, The Kuga-Satake variety of an abelian surface, J. Algebra, 92 (1985), 454–476.
A. Mokrane and J. Tilouine, Cohomology of Siegel varieties with \(p\)-adic integral coefficients and applications, Astérisque, 280 (2002), 1–95, Cohomology of Siegel varieties.
C. P. Mok and F. Tan, Overconvergent families of Siegel-Hilbert modular forms, Can. J. Math., 67 (2015), 893–922.
D. Mumford, Abelian varieties, Tata Institute of Fundamental Research Studies in Mathematics, vol. 5, Hindustan Book Agency, New Delhi, 2008, With appendices by C. P. Ramanujam and Yuri Manin, Corrected reprint of the second (1974) edition.
C. Mœglin and J.-L. Waldspurger, Stabilisation de la formule des traces tordue, vol. 1, Springer, Berlin, 2016.
C. Mœglin and J.-L. Waldspurger, Stabilisation de la formule des traces tordue, vol. 2, Springer, Berlin, 2016.
B. J. J. Moonen and Y. G. Zarhin, Hodge classes and Tate classes on simple abelian fourfolds, Duke Math. J., 77 (1995), 553–581.
S. Nakajima, On Galois module structure of the cohomology groups of an algebraic variety, Invent. Math., 75 (1984), 1–8.
B. C. Ngô and A. Genestier, Alcôves et \(p\)-rang des variétés abéliennes, Ann. Inst. Fourier (Grenoble), 52 (2002), 1665–1680.
R. Noot, The system of representations of the Weil-Deligne group associated to an abelian variety, Algebra Number Theory, 7 (2013), 243–281.
R. Noot, The \(p\)-adic representation of the Weil-Deligne group associated to an abelian variety, J. Number Theory, 172 (2017), 301–320.
S. Patrikis, Variations on a theorem of Tate, Mem. Am. Math. Soc., 258 (2019), viii+156.
V. Pilloni, Prolongement analytique sur les variétés de Siegel, Duke Math. J., 157 (2011), 167–222.
V. Pilloni, Modularité, formes de Siegel et surfaces abéliennes, J. Reine Angew. Math., 666 (2012), 35–82.
V. Pilloni, Formes modulaires \(p\)-adiques de Hilbert de poids 1, Invent. Math., 208 (2017), 633–676.
V. Pilloni, Higher coherent cohomology and \(p\)-adic modular forms of singular weights, Duke Math. J., 169 (2020), 1647–1807.
R. Pink, Arithmetical compactification of mixed Shimura varieties, Bonner Mathematische Schriften [Bonn Mathematical Publications], vol. 209, Universität Bonn, Mathematisches Institut, Bonn, 1990, Dissertation, Rheinische Friedrich-Wilhelms-Universität, Bonn, Bonn, 1989.
J. Poineau, Un résultat de connexité pour les variétés analytiques \(p\)-adiques: privilège et noethérianité, Compos. Math., 144 (2008), 107–133.
A. Pitale and R. Schmidt, Bessel models for lowest weight representations of \({\mathrm{ GSp}}(4, \Bbb {R})\), Int. Math. Res. Not., 7 (2009), 1159–1212.
V. Pilloni and B. Stroh, Cohomologie cohérente et représentations Galoisiennes, Ann. Math. Qué., 40 (2016), 167–202.
V. Pilloni and B. Stroh, Surconvergence, ramification et modularité, Astérisque, 382 (2016), 195–266.
C. Poor, J. Shurman and D. S. Yuen, Siegel paramodular forms of weight 2 and squarefree level, Int. J. Number Theory, 13 (2017), 2627–2652.
S. Patrikis and R. Taylor, Automorphy and irreducibility of some \(l\)-adic representations, Compos. Math., 151 (2015), 207–229.
S. Patrikis, J. F. Voloch and Y. G. Zarhin, Anabelian geometry and descent obstructions on moduli spaces, Algebra Number Theory, 10 (2016), 1191–1219.
C. Poor and D. S. Yuen, Paramodular cusp forms, Math. Comput., 84 (2015), 1401–1438.
D. Ramakrishnan, Modularity of the Rankin-Selberg \(L\)-series, and multiplicity one for \({\mathrm {SL}}(2)\), Ann. Math. (2), 152 (2000), 45–111.
M. Raynaud, 1-motifs et monodromie géométrique, Astérisque, 223 (1994), 295–319, Périodes \(p\)-adiques (Bures-sur-Yvette, 1988).
K. A. Ribet, Abelian varieties over \(\bf Q\) and modular forms, in Modular curves and abelian varieties, Progr. Math., vol. 224, pp. 241–261, Birkhäuser, Basel, 2004.
B. Riemann, Über die Anzahl der Primzahlen unter einer gegebenen Grösse, Monatsberichte der Berliner Akademie (1859), 671–680.
B. Roberts, Global \(L\)-packets for \({\mathrm {GSp}}(2)\) and theta lifts, Doc. Math., 6 (2001), 247–314 (electronic).
D. Ramakrishnan and F. Shahidi, Siegel modular forms of genus 2 attached to elliptic curves, Math. Res. Lett., 14 (2007), 315–332.
B. Roberts and R. Schmidt, Local newforms for GSp(4), Lecture Notes in Mathematics, vol. 1918, Springer, Berlin, 2007.
B. Roberts and R. Schmidt, Tables for representations of GSp(4), 2007, Available at http://www2.math.ou.edu/~rschmidt/papers/tables.pdf.
M. Rapoport and T. Zink, Period spaces for \(p\)-divisible groups, Annals of Mathematics Studies, vol. 141, Princeton University Press, Princeton, 1996.
T. Saito, Modular forms and \(p\)-adic Hodge theory, Invent. Math., 129 (1997), 607–620.
S. Sasaki, On Artin representations and nearly ordinary Hecke algebras over totally real fields, Doc. Math., 18 (2013), 997–1038.
W. F. Sawin, Ordinary primes for Abelian surfaces, C. R. Math. Acad. Sci. Paris, 354 (2016), 566–568.
N. I. Shepherd-Barron and R. Taylor, \({\mathrm{ mod}}\ 2\) and \({\mathrm{ mod}}\ 5\) icosahedral representations, J. Am. Math. Soc., 10 (1997), 283–298.
P. Scholze, On torsion in the cohomology of locally symmetric varieties, Ann. Math. (2), 182 (2015), 945–1066.
R. Schmidt, Archimedean aspects of Siegel modular forms of degree 2, Rocky Mt. J. Math., 47 (2017), 2381–2422.
R. Schmidt, Packet structure and paramodular forms, Trans. Am. Math. Soc., 370 (2018), 3085–3112.
C. Schembri, Examples of genuine QM abelian surfaces which are modular, Res. Number Theory, 5 (2019), 12.
R. Schmidt, Paramodular forms in CAP representations of \({\mathrm{ GSp}}(4)\), Acta Arith., 194 (2020), 319–340.
H. P. F. Swinnerton-Dyer, On \(l\)-adic representations and congruences for coefficients of modular forms, in Modular functions of one variable, III, Lecture Notes in Math., vol. 350, Proc. Internat. Summer School, Univ. Antwerp, 1972, pp. 1–55, Springer, Berlin, 1973.
J.-P. Serre, Abelian \(l\)-adic representations and elliptic curves, McGill University lecture notes written with the collaboration of Willem Kuyk and John Labute, W. A. Benjamin, Inc., New York-Amsterdam, 1968.
J.-P. Serre, Facteurs locaux des fonctions zêta des variétés algébriques (définitions et conjectures), Séminaire Delange-Pisot-Poitou. Théorie des nombres, 11 (1969–1970), 1–15 (fre).
J.-P. Serre, Formes modulaires et fonctions zêta \(p\)-adiques, in Modular functions of one variable, III, Lecture Notes in Math., vol. 350, Proc. Internat. Summer School, Univ. Antwerp, 1972, pp. 191–268, Springer, Berlin, 1973.
J.-P. Serre, Modular forms of weight one and Galois representations, in Algebraic number fields: \(L\)-functions and Galois properties, Proc. Sympos., Univ. Durham, Durham, 1975, pp. 193–268, Academic Press, London, 1977.
J.-P. Serre, Lectures on the Mordell-Weil theorem, in Aspects of Mathematics, E15, Friedr. Vieweg & Sohn, Braunschweig, 1989, Translated from the French and edited by Martin Brown from notes by Michel Waldschmidt.
J.-P. Serre, Lettre à Marie-France Vignéras du 10/02/1987. Collected papers IV, pp. 38–55, Springer, Berlin, 2000.
F. Shahidi, On non-vanishing of twisted symmetric and exterior square \(L\)-functions for \({\mathrm {GL}}(n)\), Pac. J. Math., 181 (1997), 311–322, Olga Taussky-Todd: in memoriam.
J. Shotton, The Breuil-Mézard conjecture when \(l\neq p\), Duke Math. J., 167 (2018), 603–678.
C. Skinner, A note on the \(p\)-adic Galois representations attached to Hilbert modular forms, Doc. Math., 14 (2009), 241–258.
A. Snowden, On two dimensional weight two odd representations of totally real fields, 2009, 0905.4266.
C. M. Sorensen, Galois representations attached to Hilbert-Siegel modular forms, Doc. Math., 15 (2010), 623–670.
P. J. Sally Jr. and M. Tadić, Induced representations and classifications for \({\mathrm{ GSp}}(2,F)\) and \({\mathrm {Sp}}(2,F)\), Mém. Soc. Math. Fr. (N.S.), 52 (1993), 75–133.
The Stacks Project Authors, Stacks Project, 2013, http://stacks.math.columbia.edu.
W. A. Stein, Shafarevich–Tate groups of nonsquare order, in Modular curves and abelian varieties, Progr. Math., vol. 224, pp. 277–289, Birkhäuser, Basel, 2004.
B. Stroh, Mauvaise réduction au bord, Astérisque, 370 (2015), 269–304.
J. Tate, Number theoretic background, in Automorphic forms, representations and \(L\)-functions, Part 2, Proc. Sympos. Pure Math., vol. XXXIII, Proc. Sympos. Pure Math., Oregon State Univ., Corvallis, Ore., 1977, pp. 3–26, Am. Math. Soc., Providence, 1979.
R. Taylor, Remarks on a conjecture of Fontaine and Mazur, J. Inst. Math. Jussieu, 1 (2002), 125–143.
R. Taylor, On icosahedral Artin representations. II, Am. J. Math., 125 (2003), 549–566.
R. Taylor, Automorphy for some \(l\)-adic lifts of automorphic mod \(l\) Galois representations. II, Publ. Math. IHES, 108 (2008), 183–239.
J. A. Thorne, On the automorphy of \(l\)-adic Galois representations with small residual image, J. Inst. Math. Jussieu, 11 (2012), 855–920, With an appendix by Robert Guralnick, Florian Herzig, Richard Taylor and Thorne.
J. A. Thorne, Automorphy lifting for residually reducible \(l\)-adic Galois representations, J. Am. Math. Soc., 28 (2015), 785–870.
J. Tilouine, Deformations of Galois representations and Hecke algebras, Published for The Mehta Research Institute of Mathematics and Mathematical Physics, Allahabad (1996).
J. Tilouine, Deformations of Siegel-Hilbert Hecke eigensystems and their Galois representations, in Number theory, Contemp. Math., vol. 210, Tiruchirapalli, 1996, pp. 195–225, Am. Math. Soc., Providence, 1998.
J. Tilouine, Nearly ordinary rank four Galois representations and \(p\)-adic Siegel modular forms, Compos. Math., 142 (2006), 1122–1156, With an appendix by Don Blasius.
J. Tilouine, Siegel varieties and \(p\)-adic Siegel modular forms, Doc. Math. (2006), 781–817.
J. Tilouine, Cohomologie des variétés de Siegel et représentations galoisiennes associées aux représentations cuspidales cohomologiques de \(\mathrm{ GSp}_{4}( \Bbb {Q})\), in Algèbre et théorie des nombres. Années 2007–2009, Publ. Math. Univ. Franche-Comté Besançon Algèbr. Theor. Nr., pp. 99–114, Lab. Math. Besançon, Besançon, 2009.
J. Tilouine, Formes compagnons et complexe BGG dual pour \(GSp_{4}\), Ann. Inst. Fourier (Grenoble), 62 (2012), 1383–1436.
J. Tilouine and É. Urban, Familles \(p\)-adiques à trois variables de formes de Siegel et de représentations galoisiennes, C. R. Acad. Sci. Paris, Sér. 1 Math., 321 (1995), 5–10.
J. Tilouine and É. Urban, Several-variable \(p\)-adic families of Siegel-Hilbert cusp eigensystems and their Galois representations, Ann. Sci. Éc. Norm. Supér. (4), 32 (1999), 499–574.
J. Tunnell, Artin’s conjecture for representations of octahedral type, Bull. Am. Math. Soc. (N.S.), 5 (1981), 173–175.
R. Taylor and A. Wiles, Ring-theoretic properties of certain Hecke algebras, Ann. Math. (2), 141 (1995), 553–572.
R. Taylor and T. Yoshida, Compatibility of local and global Langlands correspondences, J. Am. Math. Soc., 20 (2007), 467–493 (electronic).
É. Urban, Eigenvarieties for reductive groups, Ann. Math. (2), 174 (2011), 1685–1784.
M.-F. Vignéras, Induced r-representations of p-adic reductive groups, Sel. Math., 4 (1998), 549–623.
M.-F. Vignéras, Pro-\(p\)-Iwahori Hecke ring and supersingular
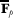 -representations, Math. Ann., 331 (2005), 523–556.
-representations, Math. Ann., 331 (2005), 523–556.
E. Viehmann and T. Wedhorn, Ekedahl-Oort and Newton strata for Shimura varieties of PEL type, Math. Ann., 356 (2013), 1493–1550.
N. R. Wallach, On the constant term of a square integrable automorphic form, in Operator algebras and group representations, Vol. II, Monogr. Stud. Math., vol. 18, Neptun, 1980, pp. 227–237, Pitman, Boston, 1984.
A. Weil, Number-theory and algebraic geometry, in Proceedings of the International Congress of Mathematicians, vol. 2, Cambridge, Mass., 1950, pp. 90–100, Am. Math. Soc., Providence, 1952.
G. Wiese, On Galois representations of weight one, Doc. Math., 19 (2014), 689–707.
A. Wiles, Modular elliptic curves and Fermat’s last theorem, Ann. Math. (2), 141 (1995), 443–551.
H. Yoshida, Siegel’s modular forms and the arithmetic of quadratic forms, Invent. Math., 60 (1980), 193–248.
H. Yoshida, On Siegel modular forms obtained from theta series, J. Reine Angew. Math., 352 (1984), 184–219.
C.-F. Yu, Irreducibility and \(p\)-adic monodromies on the Siegel moduli spaces, Adv. Math., 218 (2008), 1253–1285.
C.-F. Yu, Geometry of the Siegel modular threefold with paramodular level structure, Proc. Am. Math. Soc., 139 (2011), 3181–3190.
Author information
Authors and Affiliations
Corresponding author
Additional information
G.B. was supported in part by NSF postdoctoral fellowship DMS-1503047. F.C. was supported in part by NSF Grants DMS-1404620, DMS-1701703, and DMS-2001097. T.G. was supported in part by a Leverhulme Prize, EPSRC grant EP/L025485/1, ERC Starting Grant 306326, and a Royal Society Wolfson Research Merit Award. V.P was supported in part by the ANR-14-CE25-0002-01 Percolator, and the ERC-2018-COG-818856-HiCoShiVa.
Rights and permissions
This article is published under an open access license. Please check the 'Copyright Information' section either on this page or in the PDF for details of this license and what re-use is permitted. If your intended use exceeds what is permitted by the license or if you are unable to locate the licence and re-use information, please contact the Rights and Permissions team.
About this article
Cite this article
Boxer, G., Calegari, F., Gee, T. et al. Abelian surfaces over totally real fields are potentially modular. Publ.math.IHES 134, 153–501 (2021). https://doi.org/10.1007/s10240-021-00128-2
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10240-021-00128-2



 : wild 3-adic exercises, J. Am. Math. Soc., 14 (2001), 843–939 (electronic).
: wild 3-adic exercises, J. Am. Math. Soc., 14 (2001), 843–939 (electronic).
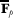 -representations, Math. Ann., 331 (2005), 523–556.
-representations, Math. Ann., 331 (2005), 523–556.