Finite element simulation of cochlear traveling wave under air and bone conduction hearing

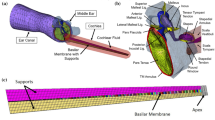
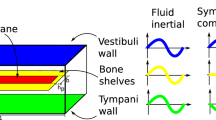
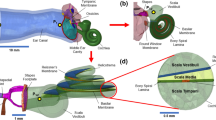
Abstract

Besides the normal hearing pathway known as air conduction (AC), sound can also transmit to the cochlea through the skull, known as bone conduction (BC). During BC stimulation, the cochlear walls demonstrate rigid body motion (RBM) and compressional motion (CPM), both inducing the basilar membrane traveling wave (TW). Despite numerous measuring and modeling efforts for the TW phenomenon, the mechanism remains unclear, especially in the case of BC. This paper proposes a 3D finite element cochlea model mimicking the TW under BC. The model uses a traditional “box model” form, but in a spiral shape, with two fluid chambers separated by the long and flexible BM. The cochlear fluid was enclosed by bony walls, the oval and round window membranes. Contingent boundary conditions and stimulations are introduced according to the physical basis of AC and BC. Particularly for BC, both RBM and CPM of the cochlea walls are simulated. Harmonic numerical solutions are obtained at multiple frequencies among the hearing range. The BM vibration amplitude ($U_{{{\text{BM}}}}$) and its relation with volume displacement difference between the oval and round windows $(\Delta {\text{Vol}})$, as well as the pressure difference at the base of the cochlea ($P_{{{\text{SV}}}} \left( 0 \right) - P_{{{\text{ST}}}} \left( 0 \right)$), are analyzed. The simulated BM response at 12 mm from the base is peaked at about 3 k Hz, which is consistent with published experimental data. The TW properties under AC and BC are the same and have a common mechanism. (1) $U_{{{\text{BM}}}}$ is proportional to ${\Delta }Vol$ at low frequencies. (2) $U_{{{\text{BM}}}}$ is also proportional to $P_{{{\text{SV}}}} \left( 0 \right) - P_{{{\text{ST}}}} \left( 0 \right)$, within 5 dB error at high frequencies such as 16 k Hz. This study partly reveals the common quantitative relations between the TW and related factors under AC and BC hearing.