Skip to main content
SpringerLink
Log in

Stability analysis of a continuum-based constrained mixture model for vascular growth and remodeling

  • Original Paper
  • Published:
Biomechanics and Modeling in Mechanobiology Aims and scope Submit manuscript

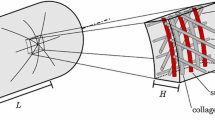
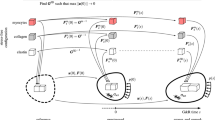
Abstract

A stabilizing criterion is derived for equations governing vascular growth and remodeling. We start from the integral state equations of the continuum-based constrained mixture theory of vascular growth and remodeling and obtain a system of time-delayed differential equations describing vascular growth. By employing an exponential form of the constituent survival function, the delayed differential equations can be reduced to a nonlinear ODE system. We demonstrate the degeneracy of the linearized system about the homeostatic state, which is a fundamental cause of the neutral stability observations reported in prior studies. Due to this degeneracy, stability conclusions for the original nonlinear system cannot be directly inferred. To resolve this problem, a sub-system is constructed by recognizing a linear relation between two states. Subsequently, Lyapunov’s indirect method is used to connect stability properties between the linearized system and the original nonlinear system, to rigorously establish the neutral stability properties of the original system. In particular, this analysis leads to a stability criterion for vascular expansion in terms of growth and remodeling kinetic parameters, geometric quantities and material properties. Numerical simulations were conducted to evaluate the theoretical stability criterion under broader conditions, as well as study the influence of key parameters and physical factors on growth properties. The theoretical results are also compared with prior numerical and experimental findings in the literature.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  • Abdul-Hussien H, Soekhoe R, Weber E, Jan H, Kleemann R, Mulder A, Van Bockel J, Hanemaaijer R, Lindeman J (2007) Collagen degradation in the abdominal aneurysm: a conspiracy of matrix metalloproteinase and cysteine collagenases. Am J Pathol 170(3):809–817

    Article  Google Scholar 

  • Aparício P, Mandaltsi A, Boamah J, Chen H, Selimovic A, Bratby M, Uberoi R, Ventikos Y, Watton P (2014) Modelling the influence of endothelial heterogeneity on the progression of arterial disease: Application to abdominal aortic aneurysm evolution. Int J Numer Methods Biomed Eng 30(5):563–586

    Article  MathSciNet  Google Scholar 

  • Austin G, Schievink W, Williams R (1989) Controlled pressure–volume factors in the enlargement of intracranial aneurysms. Neurosurgery 24(5):722–730

    Article  Google Scholar 

  • Baek S, Rajagopal K, Humphrey J (2005) Competition between radial expansion and thickening in the enlargement of an intracranial saccular aneurysm. J Elast 80(1–3):13–31

    Article  MathSciNet  MATH  Google Scholar 

  • Baek S, Rajagopal K, Humphrey J (2006) A theoretical model of enlarging intracranial fusiform aneurysms. J Biomech Eng 128(1):142–149

    Article  Google Scholar 

  • Bogen D, McMahon T (1979) Do cardiac aneurysms blow out? Biophys J 27(2):301

    Article  Google Scholar 

  • Bots M, Hofman A, de Bruyn A, De Jong P, Grobbee D (1993) Isolated systolic hypertension and vessel wall thickness of the carotid artery. The Rotterdam Elderly Study. Arterioscler Thromb Vasc Biol 13(1):64–69

    Article  Google Scholar 

  • Choke E, Cockerill G, Wilson W, Sayed S, Dawson J, Loftus I, Thompson M (2005) A review of biological factors implicated in abdominal aortic aneurysm rupture. Eur J Vasc Endovasc Surg 30(3):227–244

    Article  Google Scholar 

  • Cyron C, Humphrey J (2014) Vascular homeostasis and the concept of mechanobiological stability. Int J Eng Sci 85:203–223

    Article  Google Scholar 

  • Cyron C, Wilson J, Humphrey J (2014) Mechanobiological stability: a new paradigm to understand the enlargement of aneurysms? J R Soc Interface 11(100):20140680

    Article  Google Scholar 

  • Dijk J, Van Der Graaf Y, Grobbee D, Banga J, Bots M et al (2004) Increased arterial stiffness is independently related to cerebrovascular disease and aneurysms of the abdominal aorta the second manifestations of arterial disease (smart) study. Stroke 35(7):1642–1646

    Article  Google Scholar 

  • Etminan N, Dreier R, Buchholz B, Beseoglu K, Bruckner P, Matzenauer C, Torner J, Brown R, Steiger H, Hänggi D et al (2014) Age of collagen in intracranial saccular aneurysms. Stroke 45(6):1757–1763

    Article  Google Scholar 

  • Figueroa A, Baek S, Taylor C, Humphrey J (2009) A computational framework for fluid–solid-growth modeling in cardiovascular simulations. Comput Methods Appl Mech Eng 198(45):3583–3602

    Article  MathSciNet  MATH  Google Scholar 

  • Holzapfel G, Gasser T, Ogden R (2000) A new constitutive framework for arterial wall mechanics and a comparative study of material models. J Elast Phys Sci Solids 61(1–3):1–48

    MathSciNet  MATH  Google Scholar 

  • Huang Y, Gloviczki P, Duncan A, Kalra M, Hoskin T, Oderich G, McKusick M, Bower T (2008) Common iliac artery aneurysm: expansion rate and results of open surgical and endovascular repair. J Vasc Surg 47(6):1203–1211

    Article  Google Scholar 

  • Humphrey J (2006) Towards a theory of vascular growth and remodeling. In: Holzapfel G, Ogden R (eds) Mechanics of biological tissue. Springer, Berlin, pp 3–15. doi:10.1007/3-540-31184-X_1

  • Humphrey J (2013) Cardiovascular solid mechanics: cells, tissues, and organs. Springer, New York

    Google Scholar 

  • Humphrey J, Rajagopal K (2002) A constrained mixture model for growth and remodeling of soft tissues. Mathematical Models and Methods in Applied Sciences 12(03):407–430

    Article  MathSciNet  MATH  Google Scholar 

  • Nissen R, Cardinale G, Udenfriend S (1978) Increased turnover of arterial collagen in hypertensive rats. Proc Natl Acad Sci 75(1):451–453

    Article  Google Scholar 

  • Safar M, O’Rourke M, Frohlich E (2014) Blood pressure and arterial wall mechanics in cardiovascular diseases. Springer, Berlin

    Book  Google Scholar 

  • Satha G, Lindström S, Klarbring A (2014) A goal function approach to remodeling of arteries uncovers mechanisms for growth instability. Biomech Model Mechanobiol 13(6):1243–1259

    Article  Google Scholar 

  • Satta J, Juvonen T, Haukipuro K, Juvonen M, Kairaluoma M (1995) Increased turnover of collagen in abdominal aortic aneurysms, demonstrated by measuring the concentration of the aminoterminal propeptide of type iii procollagen in peripheral and aortal blood samples. J Vasc Surg 22(2):155–160

    Article  Google Scholar 

  • Sheidaei A, Hunley S, Zeinali-Davarani S, Raguin L, Baek S (2011) Simulation of abdominal aortic aneurysm growth with updating hemodynamic loads using a realistic geometry. Med Eng Phys 33(1):80–88

    Article  Google Scholar 

  • Valentin A, Humphrey J (2009) Evaluation of fundamental hypotheses underlying constrained mixture models of arterial growth and remodelling. Philos Trans R Soc Lond A Math Phys Eng Sci 367(1902):3585–3606

    Article  MathSciNet  MATH  Google Scholar 

  • Verhulst F (1996) Nonlinear differential equations and dynamical systems. Springer, Berlin

    Book  MATH  Google Scholar 

  • Watton P, Raberger N, Holzapfel G, Ventikos Y (2009) Coupling the hemodynamic environment to the evolution of cerebral aneurysms: computational framework and numerical examples. J Biomech Eng 131(10):101003

    Article  Google Scholar 

  • Wolinsky H (1972) Long-term effects of hypertension on the rat aortic wall and their relation to concurrent aging changes: morphological and chemical studies. Circ Res 30(3):301–309

    Article  Google Scholar 

  • Wu J, Shadden S (2015) Coupled simulation of hemodynamics and vascular growth and remodeling in a subject-specific geometry. Ann Biomed Eng 43(7):1543–1554

    Article  Google Scholar 

  • Zeinali-Davarani S, Sheidaei A, Baek S (2011) A finite element model of stress-mediated vascular adaptation: application to abdominal aortic aneurysms. Comput Methods Biomech Biomed Eng 14(9):803–817

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, University of California, Berkeley, CA, USA

    Jiacheng Wu & Shawn C. Shadden

Authors
  1. Jiacheng Wu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Shawn C. Shadden
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Shawn C. Shadden.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wu, J., Shadden, S.C. Stability analysis of a continuum-based constrained mixture model for vascular growth and remodeling. Biomech Model Mechanobiol 15, 1669–1684 (2016). https://doi.org/10.1007/s10237-016-0790-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10237-016-0790-5

Keywords

Search

Navigation