Sensitivity of tidal characteristics in double inlet systems to momentum dissipation on tidal flats: a perturbation analysis

Abstract

In a tidal channel with adjacent tidal flats, along–channel momentum is dissipated on the flats during rising tides. This leads to a sink of along–channel momentum. Using a perturbative method, it is shown that the momentum sink slightly reduces the M₂ amplitude of both the sea surface elevation and current velocity and favours flood dominant tides. These changes in tidal characteristics (phase and amplitude of sea surface elevations and currents) are noticeable if widths of tidal flats are at least of the same order as the channel width, and amplitudes and gradients of along–channel velocity are large. The M₂ amplitudes are reduced because stagnant water flows from the flats into the channel, thereby slowing down the current. The M₄ amplitudes and phases change because the momentum sink acts as an advective term during the fall of the tide, such a term generates flood dominant currents. For a prototype embayment that resembles the Marsdiep–Vlie double–inlet system of the Western Wadden Sea, it is found that for both the sea surface elevation and current velocity, including the momentum sink, lead to a decrease of approximately 2% in M₂ amplitudes and an increase of approximately 25% in M₄ amplitudes. As a result, the net import of coarse sediment is increased by approximately 35%, while the transport of fine sediment is hardly influenced by the momentum sink. For the Marsdiep–Vlie system, the M₂ sea surface amplitude obtained from the idealised model is similar to that computed with a realistic three–dimensional numerical model whilst the comparison with regard to M₄ improves if momentum sink is accounted for.

1 Introduction

In shallow coastal seas, such as the Wadden Sea in Northern Europe, the tidal motion is highly nonlinear, as is evident from the presence of residual and higher harmonics in the primary tide (Buijsman and Ridderinkhof 2007). Well-known sources of these nonlinear tides are the advection of momentum, quadratic bottom stress, depth dependent friction, divergence of excess mass (i.e. mass stored between mean sea level and actual sea surface) and the hypsometry of the embayment (e.g. Parker1991; Friedrichs and Aubrey1994, and references therein). As a result, the sinusoidal shape of the curves of the sea surface height and current velocity at a fixed location is distorted. This tidal asymmetry leads to a net transport of fine and coarse sediment (Groen 1967; Aubrey 1986; Boon and Byrne 1981; van de Kreeke and Robaczewska 1993).

In this study, the focus is on nonlinear tides by hypsometry and in particular by dissipation of momentum on tidal flats. When the water level rises, water flows from the channel onto the flats, carrying with it longitudinal momentum. The mass is temporarily stored on the flats, until it flows back into the channel during the falling tide. The momentum, on the other hand, dissipates rapidly due to high friction on the tidal flats. That is, the flats act like mass storages and momentum sinks (Dronkers and Schönfeld 1959; Dronkers 1964).

In contrast to mass storage, which has been extensively studied (Speer and Aubrey 1985; Friedrichs and Aubrey 1994; Ridderinkhof et al. 2014), the role of the momentum sink on tidal dynamics is less well understood. Numerical model studies (e.g. Brown and Davies2010) show that tidal asymmetry strongly depends on the distribution of channels and flats, thereby suggesting the importance of processes such as the momentum sink. de Swart et al. (2011) and Alebregtse (2015)¹ studied numerically the momentum sink in a semi-enclosed embayment. They demonstrated that the amount by which the momentum sink deforms tidal curves depends on the ratio of flat–to–channel area, the shape of the tidal flats and the distribution of flats along the channel. However, no details about the underlying processes were given.

The considerations above motivate further investigation of the generation of overtides by a momentum sink, which is conducted here. Similar to Alebregtse (2015), the model of Speer and Aubrey (1985) is extended with a momentum sink term. The model of Speer and Aubrey (1985) has been successfully validated against field data (see also Friedrichs and Aubrey1988, 1994). Here, two main new aspects are introduced. First, the approach is analytic in nature, and approximate solutions of the cross-sectionally averaged shallow water equations are explicitly constructed using perturbation methods that exploit the smallness of the Froude number. This enables the assessment of the impact of the momentum sink and quantification of the difference between solutions that do and do not account for it. Second, a double inlet system (rather than a semi-enclosed bay) with an M₂ tidal wave entering at both ends is considered. In particular, this permits investigating what happens in double inlet systems when the two waves entering at opposite sides differ in amplitude or phase, as typically occurs in nature. Examples of such embayments are the Western Wadden Sea in the Netherlands, with the Marsdiep and Vlie inlets (e.g. Ridderinkhof1988, also considered here), the Laguna de Términos in México (David and Kjerfve 1998) and the Santa María La Reforma in California (Serrano et al. 2013).

This study has two specific aims. The first is to assess changes in tidal characteristics of sea surface elevation and current velocity due to the momentum sink in double inlet systems with different parameter settings. The parameters that will be varied are the width of the tidal flats and the channel width, the drag coefficient, the slope of the flats, the phase difference between the incoming tidal waves and the length of the embayment. The second aim is to understand the mechanisms behind these changes in tidal characteristics.

The paper is organised as follows. In Section 2, the model is presented. In Section 3, a perturbation method is used to find approximate solutions to the cross-sectionally averaged shallow water equations. The results are presented in Section 4, followed by a discussion in Section 5. Here, mechanisms leading to the model results are explained together with a qualitative comparison with the model output of a complex numerical model. Section 6 contains the conclusions.

2 Model formulation

2.1 Physical domain and geometry

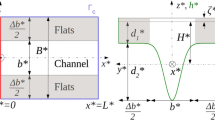
The tidal embayment considered in this study consists of a channel of constant width $b_{c}^{\ast }$ with adjacent tidal flats. The embayment is connected to an open sea on both sides, has length L^∗ and geometry symmetric with respect to the centerline of the channel (see Fig. 1).

Fig. 1

Geometry of the open embayment (a sideview at any longitudinal position, b topview). Here, $b_{{\max }}^{\ast }$ is the width of the embayment including the dry parts of the flats, b^∗(t^∗) the width of the wetted part of the embayment and $b_{c}^{\ast }$ the width of the channel. Furthermore, h^∗ is the undisturbed depth (being $h_{c}^{\ast }$ in the channel and $d_{f}^{\ast }$ on the flats), φ the angle of inclination of the flats, L^∗ the length of the embayment and ζ^∗ the sea surface elevation. The origin is at the intersection of the dotted lines. In (a), the x^∗ axis points into the paper. The blue area in (b) is the wetted part

The along–channel coordinate is x^∗, the lateral coordinate y^∗, the vertical coordinate z^∗ and the time coordinate t^∗. The origin is placed in the middle of the embayment at the height of the undisturbed sea level. The undisturbed water depth on the flats is $d_{f}^{\ast }$ and in the channel it is $h_{c}^{\ast }$. The width of the channel or of the flats henceforth refers to the width of the wetted part of the channel or flats. The total width b^∗ of the embayment is dependent on the sea surface elevation ζ^∗, and hence also on t^∗ and x^∗. The geometry of the cross section is based on that of Speer and Aubrey (1985). It is assumed that the lowest part of the flats are located at the level of low water. The total width reads

$$ b^{\ast} = b_{{\max}}^{\ast} - \frac{2d_{f}^{\ast}}{\tan{\varphi}}\left( 1 - \frac{\zeta^{\ast}}{d_{f}^{\ast}}\right), $$

(1)

where, $b_{{\max }}^{\ast }$ is the width of the embayment including the dry parts of the flats and φ the angle of inclination of the flats as in Fig. 1. It follows from the figure that partly horizontal flats with a kink are possible if

$$\varphi \geq \tan^{-1}\left( \frac{4d_{f}^{\ast}}{b_{{\max}}^{\ast}-b_{c}^{\ast}}\right).$$

This motivates the introduction of a parameter q ≥ 1 defined as

$$q = \tan(\varphi)\frac{b_{{\max}}^{\ast} - b_{c}^{\ast}}{4d_{f}^{\ast}}.$$

The total width of the embayment now reads

$$ b^{\ast} = b_{{\max}}^{\ast} - \frac{b_{{\max}}^{\ast}-b_{c}^{\ast}}{2q}\left( 1 - \frac{\zeta^{\ast}}{d_{f}^{\ast}}\right). $$

(2)

The parameter q ≥ 1 determines flat steepness; q = 1 means linear flats and larger q values imply steeper flats (in Fig. 1, q = 5).

2.2 Governing equations

The hydrodynamics in the embayment are modelled by the cross-sectionally averaged shallow water equations. They read

$$ \frac{b^{\ast}}{b_{c}^{\ast}}\frac{\partial \zeta^{\ast}}{\partial t^{\ast}} + \frac{\partial (\zeta^{\ast}+h_{c}^{\ast})u^{\ast}}{\partial x^{\ast}} = 0, $$

(3)

$$ \frac{\partial u^{\ast}}{\partial t^{\ast}} + u^{\ast} \frac{\partial u^{\ast}}{\partial x^{\ast}} + g^{\ast}\frac{\partial \zeta^{\ast}}{\partial x^{\ast}} { {+}} \frac{r^{\ast} u^{\ast}}{\zeta^{\ast}+h_{c}^{\ast}} = { {M^{\ast}}}, $$

(4)

with

$$ M^{\ast} = \frac{b^{\ast} - b_{c}^{\ast}}{b_{c}^{\ast}}\frac{u^{\ast}}{\zeta^{\ast}+h_{c}^{\ast}}\frac{\partial \zeta^{\ast}}{\partial t^{\ast}}\mathscr{H}\left( -\frac{\partial \zeta^{\ast}}{\partial t^{\ast}}\right). $$

(5)

Here, u^∗ (ms^− 1) is the current velocity averaged over the cross-section of the channel (excluding the flats) in the along–channel (x^∗) direction, ζ^∗ (m) is the sea surface elevation, g^∗ (m s^− 2) is the gravitational acceleration, r^∗ (ms^− 1) is a friction parameter and $\mathscr {H}$ is the step or Heaviside function, which is one (zero) when its argument is positive (negative). Further, M^∗ is the momentum sink term which is derived and put into context of previous studies in Appendix A.

In Eqs. 3–5, it is assumed that the channel width $b_{c}^{\ast }$ is constant, the water in the channel has a constant density, there is no effect of wind or waves and the stresses that result from averaging nonlinear momentum fluxes over the cross section can be ignored. On the tidal flats, the velocity in the along–channel direction is assumed to be zero. Instead of a quadratic bottom stress $\tau _{b}^{\ast } = \rho ^{\ast } c_{d} |u^{\ast }|u^{\ast }$, with c _d a drag coefficient and ρ^∗ the water density, a linear stress $\tau _{b}^{\ast } = \rho ^{\ast } r^{\ast } u^{\ast }$ is used to allow for analytical approximations. The friction parameter r^∗ is determined by demanding that the energy dissipated in one tidal cycle (averaged over the spatial domain) is to be the same in both formulations (e.g. Lorentz1922; Terra et al. 2005). Thus,

$$ {\int}_{-L^{\ast}/2}^{L^{\ast}/2}\langle c_{d} |u^{\ast}|u^{\ast2}\rangle\,dx^{\ast} = {\int}_{-L^{\ast}/2}^{L^{\ast}/2}\langle r^{\ast} u^{\ast2}\rangle \, dx^{\ast}, $$

(6)

in which 〈⋅〉 denotes the average over one tidal cycle. As, a priori, u^∗ is not known, r^∗ is determined iteratively.

The system of Eqs. 1–5 will be considered in the weakly nonlinear regime, i.e. magnitudes of nonlinear terms are small compared to those of linear terms. In that case, as will be shown in Section 3, solutions consist of waves that propagate in both the positive and negative x–direction. The (Riemann) boundary conditions are that at both open sides of the embayment, a prescribed T^∗–periodic tidal wave (where T^∗ = 2π/σ^∗, with σ^∗ the M₂ tidal frequency) propagates into the embayment and that waves may freely exit the domain. This choice implies that boundary conditions are independent of the dynamics inside the domain.

Furthermore, it is imposed that the average volume of water over one tidal period is constant and that there is no net transport of water through the embayment. The former poses a condition for the residual sea surface elevation and the latter a condition for the residual current velocity.

3 Model analysis

Equations 3–5 are nonlinear and cannot be solved analytically, necessitating the derivation of approximate solutions, either numerical or perturbative. The former have the advantage that they remain valid over extended regions in parameter space, as they do not require nonlinear terms to be much smaller than the linear ones. The benefit of perturbative methods is that they result in closed form solutions that yield information about the effect of different physical forcing terms on solutions. As mentioned in Section 1, here a perturbation analysis is made. For this, dimensionless equations containing a small parameter are needed in which all variables are of order 1. Let

$$ u= \frac{u^{\ast}}{\mathcal{U}}, \; \zeta = \frac{\zeta^{\ast}}{\mathcal{Z}}, \; x = \frac{x^{\ast}}{\mathcal{L}}~\text{and}~ t = \frac{t^{\ast}}{\mathcal{T}} $$

(7)

be dimensionless variables, where

$$ \mathcal{U} = \mathcal{Z}\sqrt{\frac{g^{\ast}}{h_{c}^{\ast}}}, \; \mathcal{Z} = {{d_{f}^{\ast}}}, \; \mathcal{L} = \frac{\sqrt{g^{\ast} h_{c}^{\ast}}}{\sigma^{\ast}} ~\text{and}~ \mathcal{T} = \frac{1}{\sigma^{\ast}}. $$

(8)

The scales $\mathcal {U}$ and $\mathcal {Z}$ are typical values for the current velocity and the sea surface elevation amplitude, respectively. The scales $\mathcal {L}$ and $\mathcal {T}$ are typical values for a frictionless tidal wave length and period of the principal constituent (both divided by 2π), quantifying the length and time scale of the dominant dynamics. The scaled versions of Eqs. 3–4 are

$$ (1+ \beta - \beta\alpha\varepsilon(1- \zeta))\frac{\partial \zeta}{\partial t} + \frac{\partial}{\partial x}\left[(1+\varepsilon\zeta)u\right] = 0,\\ $$

(9)

$$\begin{array}{@{}rcl@{}} && \frac{\partial u}{\partial t} + \varepsilon u \frac{\partial u}{\partial x} +\frac{\partial \zeta}{\partial x} + \frac{ru}{1+\varepsilon\zeta}\\ &&\quad-\varepsilon\beta\frac{u}{1+\varepsilon\zeta}\frac{\partial \zeta}{\partial t}\mathscr{H}\left( -\frac{\partial \zeta}{\partial t}\right) = 0. \end{array} $$

(10)

The Froude number is denoted by ε:

$$ \varepsilon = \frac{\mathcal{Z}}{h_{c}^{\ast}} = \frac{\mathcal{U}}{\sqrt{g^{\ast} h_{c}^{\ast}}}. $$

(11)

In many tidal embayments (e.g., the Wadden Sea), ε is around 10^− 1 and here assumed to be a small parameter. The dimensionless length of the channel is $L = L^{\ast }/\mathcal {L}$. Furthermore,

$$ \beta = \frac{b_{{\max}}^{\ast} - b_{c}^{\ast}}{b_{c}^{\ast}},\; \alpha\varepsilon = \frac{1}{2q}, ~\text{and}~\; r = \frac{r^{\ast} \mathcal{T}}{h_{c}^{\ast}}. $$

(12)

The parameter β is the ratio of the tidal flat width to the main channel width, the parameter α controls the steepness of the sides of the flats and r is the dimensionless friction parameter. It is assumed that the area of the flats is of the same order as the channel area, that the slope of the tidal flats is steep and that friction is moderate. The consequence of these choices are that the magnitude of the momentum sink and mass storage are comparable with that of other nonlinear terms in the equations of motion, such as advection. Note that Friedrichs and Aubrey (1994) and Speer and Aubrey (1985) assume β to be small. However, inlet systems like those in the Wadden Sea are characterised by β ≈ 2 (Dronkers 2005). Thus, it is assumed that

$$\beta, \alpha, r = O(1), $$

where the symbol O(1) denotes that they are of order 1. Moreover, O(ε) parts of the friction parameter r and the O(ε²) parts of the last term in Eq. 10 are neglected. All dimensionless variables are assumed to be of order 1, so the magnitude of the terms in the dimensionless equations is determined by the parameters they involve.

The Lorenz linearisation condition (6) in dimensionless variables reads

$$ \frac{\mathcal{U}h_{c}^{\ast} c_{d}}{\mathcal{T}} {\int}_{-L/2}^{L/2} \langle |u|u^{2} \rangle \,dx = r {\int}_{-L/2}^{L/2} \langle u^{2} \rangle \,dx, $$

(13)

with the additional assumption that

$$\frac{\mathcal{U}h_{c}^{\ast} c_{d}}{\mathcal{T}} = O(1). $$

Substituting the perturbation series u = u₀ + εu₁ + ⋯ and ζ = ζ₀ + εζ₁ + ⋯ in Eqs. 9–10 and collecting terms of order 1, one obtains the so-called O(1) problem. Likewise, collecting terms of order ε yields the O(ε) problem. The O(1) and O(ε) problem will be treated separately in the following sections.

3.1 The O(1) problem

The O(1) problem is linear and reads

$$\begin{array}{@{}rcl@{}} (1+\beta)\frac{\partial \zeta_{0}}{\partial t} + \frac{\partial u_{0}}{\partial x} &= 0, \end{array} $$

(14)

$$\begin{array}{@{}rcl@{}} \frac{\partial u_{0}}{\partial t} + \frac{\partial \zeta_{0}}{\partial x} + r u_{0} &= 0, \end{array} $$

(15)

hence, it admits nontransient solutions of the form

$$ { {(\zeta_{0}(x,t),u_{0}(x,t)) = \text{Re}\left\{ {(\hat{\zeta}_{0}(x),\hat{u}_{0}(x)) e^{-it}} \right\},}} $$

(16)

with $\hat {\zeta }_{0}(x)$ and $\hat {u}_{0}(x)$ complex amplitudes and Re{⋅} denoting the real part of a complex number. Equation 16 describes the primary tidal wave in the system. By eliminating u₀ from Eqs. 14–15 and substituting ζ₀ from Eq. 16, an ordinary differential equation (ODE) for $\hat {\zeta }_{0}$ is found:

$$ \frac{\partial^{2} \hat{\zeta}_{0}}{\partial x^{2}} + k^{2} \hat{\zeta}_{0} = 0, $$

(17)

with complex wave number k satisfying k² = (1 + β)(1 + ir). This has the general solution

$$ \hat{\zeta}_{0}(x) = A e^{ikx} + Be^{-ikx}, $$

(18)

where A and B are complex–valued integration constants. When Eq. 18 is substituted into Eq. 16, and choosing the root with positive real part (i.e, Re{k} > 0), it follows that the first term on the right hand side of Eq. 18 describes the spatial structure of a right–propagating wave, while the second term describes the structure of a left–propagating wave. Equations 14–15 allow for solutions that consist of waves propagating in opposite directions. Following the considerations in Section 2, conditions at both the left (x = −L/2) and right (x = L/2) boundary are imposed on the waves that enter the domain. At the left boundary, the incoming wave progressing to the right has a sea surface elevation amplitude z _l . At the right boundary a left–propagating tidal wave enters with a sea surface elevation amplitude of z _r . The phase difference between the incoming tidal waves at the boundary is 𝜃. Hence, the sea surface variations corresponding to right–propagating wave at x = −L/2 and the left–propagating wave at x = L/2 are, respectively,

$${ {z_{l}\cos(\text{Re}\left\{ {k} \right\}x-t)\quad \text{and}\quad z_{r}\cos(\text{Re}\left\{ {k} \right\}x+t -\theta)}}.$$

Thus, high water related to the incoming wave at the left boundary occurs at time t = −Re{k}L/2 and at the right boundary it occurs a time 𝜃 later. These boundary conditions are met by choosing

$$ A = z_{l}e^{-\text{Im}\left\{ {k} \right\}\frac{L}{2}} \quad\text{and}\quad B = z_{r}e^{-\text{Im}\left\{ {k} \right\}\frac{L}{2}+ i \theta} , $$

(19)

with Im{⋅} denoting the imaginary part of a complex number. Note that, when 𝜃 = 0 and z _l = z _r , the two incoming waves have equal phase and amplitude. In that symmetric case, the velocity u₀ vanishes in the middle of the channel (at x = 0) and water motion in half the embayment (from x = −L/2 to x = 0) behaves as if in a semi-enclosed embayment with the left–propagating wave representing the wave reflected at the closed boundary. Once the sea surface elevation ζ₀ is known, the along–channel current velocity u₀ follows from either Eq. 14 or Eq. 15 using Eq. 16,

$$ \hat{u}_{0}(x) = \frac{ik}{i - r}\left( A e^{ikx} - Be^{-ikx}\right). $$

(20)

As mentioned in Section 2.2, the friction parameter r is determined from the Lorentz linearisation condition (13). First, u₀ is calculated with Eq. 20–16, using an initial guess for r. Next, r is updated to satisfy Eq. 13, with u = u₀ and the integrals are calculated numerically. A new value for u₀ is calculated using this updated value for r, and the process is iterated until the relative change in r between successive iterations is less than 0.0001%. This r–value is also used in the O(ε) problem below.

3.2 The O(ε) problem

The O(ε) problem reads

$$ (1+\beta)\frac{\partial \zeta_{1}}{\partial t} + \frac{\partial u_{1}}{\partial x} = \underbrace{-\frac{\partial} {\partial x}(u_{0}\zeta_{0})}_{\mathrm{I}} \underbrace{+ \beta\alpha(1-\zeta_{0})\frac{\partial \zeta_{0}}{\partial t}}_{\text{II}}, $$

(21)

$$\begin{array}{@{}rcl@{}} &&\frac{\partial u_{1}}{\partial t} + \frac{\partial \zeta_{1}}{\partial x} + r u_{1} \\ &&= \underbrace{-u_{0}\frac{\partial u_{0}}{\partial x} \vphantom{\left( \frac{\partial}{\partial}\right)}}_{\text{III}} \underbrace{+ ru_{0}\zeta_{0} \vphantom{\left( \frac{\partial}{\partial}\right)}}_{\text{IV}} \underbrace{+ \beta u_{0}\frac{\partial \zeta_{0}}{\partial t}\mathscr{H}\left( -\frac{\partial \zeta_{0}}{\partial t}\right)}_{\mathrm{V}}. \end{array} $$

(22)

These equations have the same form as those of the O(1) problem, but with the known O(1) solutions forcing the unknowns u₁ and ζ₁ through the inhomogeneous terms on the right hand side of Eqs. 21–22. Every term in the inhomogeneity originates from nonlinear terms in Eqs. 9–10. In Table 1, the physical source of every nonlinear term is presented.

Table 1 Source of the forcing terms

Since the inhomogeneities I, II, III and IV in the O(ε) problem consist of products of the O(1) solutions, which themselves are M₂ signals, they are composed of M₀ and M₄ harmonics. Term V is different from terms I–IV in the sense that it is not quadratic. Because of the presence of the discontinuous step function $\mathscr {H}$, that term consists of an infinite number of harmonics,

$$ \beta u_{0}\frac{\partial \zeta_{0}}{\partial t}\mathscr{H}\left( -\frac{\partial \zeta_{0}}{\partial t} \right) = \sum\limits_{m=-\infty}^{\infty} p_{m} e^{-imt}, $$

(23)

where the complex coefficients p _m are given in Appendix B. Note that p _m depends in a nonlinear way on β through ζ₀ and u₀. The nontransient solution of the O(ε) problem has the form

$$\begin{array}{@{}rcl@{}}(\zeta_{1}(x,t),u_{1}(x,t)) \!&= &\!(\langle \zeta_{1}\rangle(x) , \langle u_{1} \rangle(x))\\ &&\!+ \sum\limits_{m = 1}^{\infty} \text{Re}\left\{ {(\hat{\zeta}_{1,m}(x),\hat{u}_{1,m}(x))e^{-imt}} \right\}\!.\\ \end{array} $$

(24)

In the remainder of this section, $\langle \zeta _{1} \rangle , \langle u_{1} \rangle , \hat {\zeta }_{1,m}$ and $\hat {u}_{1,m}$ are calculated.

The residual current velocity 〈u₁〉 is determined by averaging Eq. 21 over a tidal cycle using the condition that there is no net transport of water, 〈u(1 + εζ)〉 = 0. So, the residual current only compensates for Stokes transport created by the tidal wave. This yields

$$ \langle u_{1} \rangle = -\langle u_{0}\zeta_{0}\rangle = \underbrace{-\frac{1}{2}|\hat{u}_{0}||\hat{\zeta}_{0}|\cos(\phi_{\hat{u}_{0}} - \phi_{\hat{\zeta}_{0}})}_{\mathrm{I}}, $$

(25)

where $|\hat {u}_{0}|$ and $\phi _{\hat {u}_{0}}$ are the amplitude and phase of the O(1) current velocity $\hat {u}_{0}$. Likewise, $|\hat {\zeta }_{0}|$ and $\phi _{\hat {\zeta }_{0}}$ are the amplitude and phase of the O(1) sea surface elevation $\hat {\zeta }_{0}$.

The residual sea surface elevation 〈ζ₁〉 results from the tidal average of Eq. 22 and imposing the condition that the average volume of water over one tidal period remains the same, ${\int }_{-L/2}^{L/2}\langle \zeta _{1}\rangle \,dx = 0$,

$$ \langle\zeta_{1}\rangle = -\frac{1}{L}{\int}_{-L/2}^{L/2} {{\int}_{0}^{x}} E(s)\, ds \, dx + {{\int}_{0}^{x}} E(s) \, ds\\ $$

(26)

with

$$\begin{array}{@{}rcl@{}} E(x) &=& \underbrace{-\frac{1}{4}\frac{\partial|\hat{u}_{0}|^{2}}{\partial x}}_{\text{III}} + |\hat{u}_{0}||\hat{\zeta}_{0}|\left( \underbrace{\vphantom{\frac{1}{4}} r\cos(\phi_{\hat{u}_{0}}- \phi_{\hat{\zeta}_{0}})}_{\text{IV}} \right.\\ &&\left. \quad - \underbrace{\frac{\beta}{4}\sin(\phi_{\hat{u}_{0}} - \phi_{\hat{\zeta}_{0}})}_{\mathrm{V}}\right). \end{array} $$

(27)

In Eq. 26, the variable s is used as a dummy variable for x. It follows from Eq. 27 that advection of momentum (III), depth dependent bottom friction (IV) and momentum sink (V) lead to residual sea surface elevation.

In order to obtain solutions for $\hat {\zeta }_{1,m}$, Eq. 24 is substituted into Eqs. 21–22. Subsequently, u₁ is eliminated, which results in an ODE for every $\hat {\zeta }_{1,m}$,

$$ \frac{\partial^{2} \hat{\zeta}_{1,m}}{\partial x^{2}} + (k_{m} )^{2}\hat{\zeta}_{1,m} = f_{m}(x), $$

(28)

with (k _m )² = (1 + β)m(m + ri) and

$$ f_{1} = \underbrace{\vphantom{\frac{\partial}{\partial}} 2\beta\alpha\hat{\zeta}_{0}}_{\text{II}} \underbrace{ + 2\frac{\partial p_{1}}{\partial x}}_{\mathrm{V}}, $$

(29)

$$ f_{2} = \underbrace{ -i\frac{\partial(\hat{u}_{0}\hat{\zeta}_{0})}{\partial x}}_{\mathrm{I}} \underbrace{ - \frac{1}{4}\frac{\partial^{2}\hat{u}_{0}^{2}}{\partial x^{2}}} _{\text{III}} \underbrace{ + r\frac{\partial(\hat{u}_{0}\hat{\zeta}_{0})}{\partial x}}_{\text{IV}} \underbrace{\vphantom{\frac{\partial}{\partial x}} -2\beta\alpha\hat{\zeta}_{0}^{2}}_{\text{II}} \underbrace{ + 2\frac{\partial p_{2}}{\partial x}}_{\mathrm{V}}, $$

(30)

$$ f_{m\geq3} = \underbrace{2\frac{\partial p_{m}}{\partial x}}_{\mathrm{V}}. $$

(31)

It follows from Eqs. 29–31 that advection of momentum (III), depth dependent bottom friction (IV) and divergence of excess mass (I) create an M₄ harmonic in the sea surface elevation. The mass storage on the tidal flats (II) generates M₂ and M₄. The momentum sink (V) generates M₂, M₄, M₆, M₁₀, M₁₄, M₁₈, …. The momentum sinks skips generation of M₈, M₁₂, M₁₆, …, because p _m = 0 if m > 2 and even. Solutions of the ODEs in Eq. 28 are obtained using variation of parameters,

$$\begin{array}{@{}rcl@{}} \hat{\zeta}_{1,m} &=& { {C_{m} e}}^{{ {ik_{m}x}}} + { {D_{m}e}}^{{ {-ik_{m}x}}}\\ && + \frac{e^{i k_{m} x}}{2i k_{m}}{\int}_{-L/2}^{x} \!\!\!\!\!\!\!e^{-i k_{m} s} f_{m}(s) \, ds\\ &&+ \frac{e^{-i k_{m} x}}{2i k_{m}}{\int}_{x}^{L/2}\!\!\!\!\!e^{i k_{m} s} f_{m}(s) \, ds, \end{array} $$

in which C _m and D _m are complex–valued integration constants. The boundary conditions for the O(ε) problem (21)–(22) are similar as those for the O(1) problem. At x = −L/2, it is imposed that the M_2m tidal wave that enters the domain has sea surface amplitude z_l,m. Similarly, at the right boundary (x = L/2) a left–propagating M_2m tidal wave enters with a given sea surface amplitude z_r,m and a phase shift 𝜃 _m with respect to the incoming wave at the left boundary. These conditions are met when

$$C_{m} = z_{l,m}e^{-\text{Im}\left\{ {k_{m}} \right\}\frac{L}{2}} \quad\text{and } D_{m} = z_{r,m}e^{-\text{Im}\left\{ {k_{m}} \right\}\frac{L}{2}+i\theta_{m}}. $$

To study the overtides generated inside the domain by incoming M₂ waves, z_l,m and z_r,m are chosen to be zero, except when the comparison is made with a complex numerical model in Section 5.3.

The complex amplitudes $\hat {u}_{1,m}$ of the O(ε) current velocity u₁ are found by substituting Eq. 24 in Eq. 22. This yields

$$ \hat{u}_{1,2} = \frac{1}{2i -r} \left( \underbrace{\frac{1}{4}\frac{\partial \hat{u}_{0}^{2}}{\partial x}}_{\text{III}} + \frac{\partial \hat{\zeta}_{1,2}}{\partial x} \underbrace{- \frac{r}{2}\hat{u}_{0}\hat{\zeta}_{0}}_{\text{IV}} \underbrace{\vphantom{\frac{1}{4}} - 2p_{2}}_{\mathrm{V}} \right), $$

(32)

$$ \hat{u}_{1,m\neq2} = \frac{1}{im - r} \left( \frac{\partial \hat{\zeta}_{1,m}}{\partial x} - \underbrace{2p_{m}}_{\mathrm{V}}\right). $$

(33)

It follows from these expressions that advection of momentum (III), depth dependent bottom friction (IV) create M₄ velocities and the momentum sink (V) generates M₂, M₄, M₆, M₁₀, … velocities.

4 Results

In order to address the two objectives set out in Section 1, parameter values will be chosen that are representative of a prototype double inlet system, viz. the Marsdiep–Vlie system in the Western Wadden Sea. The embayment is roughly 60 km long, 15 km wide and the channel has an averaged depth of 10 m. The primary tide is the semi–diurnal lunar tide M₂ and its first overtide M₄ is clearly present (Buijsman and Ridderinkhof 2007). The total tidal range is around 1.4 m at the Marsdiep and 1.8 m at the Vlie and the moment of high water at the Marsdiep differs by approximately 90 min from that at the Vlie (Royal Netherlands Navy 2016). The default parameter values used are listed in Table 2.

Table 2 Default setting of parameters, representative of the Marsdiep–Vlie embayment. Sources for these values are Dronkers (2005) and Royal Netherlands Navy (2016)

4.1 Impact of the momentum sink on tides in the default setting

In Fig. 2, results are shown of the primary tide M₂ and its first overtide M₄ of the sea surface elevation and current velocity in the regime where all forcings in Eqs. 21–22 are taken into account and for the case where the momentum sink is turned off (term V = 0). Panels (a) and (c) of this figure reveal that including the momentum sink lowers the M₂ amplitude and increases the M₄ amplitude of both the sea surface elevation and the current velocity of the order of centimetres, respectively, centimetres per second. For the M₂ amplitudes, that change is approximately 2%, for the M₄ amplitudes, approximately 25%. The increase in absolute value of the residual sea surface elevation due to the momentum sink is of the order of 0.5 cm, corresponding to a relative change of 30%. Note that in Fig. 2a, c, the M₂ amplitude of both the sea surface elevation and the current velocity at the left boundary differs from that at the right boundary, even though the amplitudes of the incoming tidal waves at the boundaries are equal.

Fig. 2

a, b Amplitude and phase of the sea surface elevation ζ^∗ versus distance x^∗, for different harmonics M₀, M₂ and M₄ and for the default parameter setting (Table 2). The solid line represents the solution accounting for all the nonlinear terms (I–V), including the momentum sink (term V). The dashed line represents the solution with the momentum sink neglected. The shaded area marks the difference between them. c, d As (a) and (b), but for the current velocity u^∗

Figure 2b, d reveal that the M₂ phase of both the sea surface elevation and the current velocity is hardly influenced. However, the phase of the M₄ component of the sea surface elevation is lowered by approximately 15^∘. The phase of the M₄ harmonic of the velocity is lowered by approximately 10^∘. Figure 2b illustrates that the M₂ sea surface elevation has the character of a propagating wave near the boundaries, but it turns into a standing wave in the middle of the channel as the phase becomes constant there. The M₄ component of the sea surface elevation has the character of a standing wave with a jump in phase around x^∗ = − 6 km. Both the M₂ and M₄ components of the current velocity have the character of standing waves with jumps in phase around x^∗ = 15 km.

4.2 Impact of the momentum sink on sediment transport

Changes in tidal harmonics as described above may lead to a difference in sediment transport. The net sediment transport due to the primary tide and its first overtide is calculated as in de Swart and Zimmerman (2009) (after Groen1967),

$$\begin{array}{@{}rcl@{}} \langle S^{\ast} \rangle & =& \frac{\nu^{\ast}}{4\gamma^{\ast}}U^{\ast2}_{M_{2}}U^{\ast}_{M_{4}}\cos(\tau)\left( \frac{2}{1+a^{2}} + \frac{1}{1 + 4a^{2}}\right) \\ && - a\frac{\nu^{\ast}}{2\gamma^{\ast}}U^{\ast2}_{M_{2}}U^{\ast}_{M_{4}}\sin(\tau)\left( \frac{1}{1+a^{2}} + \frac{1}{1 + 4a^{2}}\right),\\ \end{array} $$

(34)

with ν^∗ (s m^− 1) an erosion parameter and γ^∗ (s^− 1) a settling parameter (1/γ^∗ is the timescale in which sediment settles to the bed), a = σ^∗/γ^∗, $\tau = \arg (\varepsilon \hat {u}_{1,2}) - 2\arg (\hat {u}_{0} + \varepsilon \hat {u}_{1,1})$ the relative phase of the M₂ and M₄ harmonic, and $U^{\ast }_{M_{2}} = \mathcal {U}|\hat {u}_{0} +\varepsilon \hat {u}_{1,1}|$ and $U^{\ast }_{M_{4}} = \mathcal {U}|\varepsilon \hat {u}_{1,2}|$ the M₂ and M₄ amplitude of the current velocity. Coarse sediment is characterised by a small a ≈ 0.01, while a ≈ 5 is representative for fine sediment. Figure 3 shows the tidally averaged volumetric sediment transport per unit mass and width 〈S^∗〉, divided by ν^∗/4γ^∗, both for when the momentum sink is included and when it is not. The purple lines shows the situation with coarse sediment and the red ones the situation with fine sediment. The arrows indicate the direction of the sediment transport. The figure reveals that including the momentum sink increases the absolute value of the transport of coarse sediment by approximately 35% and has little impact on the transport of fine sediment. On the left (right) side of the channel, the flood current is to the right (left). Hence, the momentum sink increases transport of coarse sediment in the flood direction, that is, it leads to an import of coarse sediment. Furthermore, Fig. 3 shows that fine sediment is transported through the embayment, from the right boundary to the left boundary. Coarse sediment accumulates around x^∗ = 5 km and suggests the formation of a tidal watershed at this location.

Fig. 3

Tidally averaged sediment transport 〈S^∗〉, divided by (ν/4γ), versus distance x^∗. The purple lines shows the transport of coarse sediment, a = 0.01 and red the one of fine sediment, a = 5. The solid line represents the solution with the momentum sink taken into account and the dashed line the solution where it is not. The arrows illustrate the direction of the sediment transport and indicate the formation of a shoal at x^∗ = 5 km. Values of the remaining parameters are those in Table 2

4.3 Sensitivity study

In this section, it is investigated how sensitive the results of the preceding section are to changes in model parameters. The difference in amplitude due to the momentum sink is henceforth denoted by ΔAmpl.

Figure 4 shows ΔAmpl in sea surface elevation for various harmonics as a function of x^∗ and for different values of flat–to–channel area ratio β, slope parameter α and drag coefficient c _d . Red colours denote an increase and blue colours a decrease in amplitude. Figure 5 is similar to Fig. 4, but for the current velocity instead of the sea surface elevation. The difference in phase due to the momentum sink is not shown since it remains close to zero for the M₂ harmonic and close to 10^∘–15^∘ for the M₄ harmonic when the parameters β, α and c _d are varied. The M₀ component of the current velocity is also left out since Eq. 25 already shows that ΔAmpl = 0.

Fig. 4

Contours of the momentum sink–induced amplitude difference ΔAmpl in sea surface elevation versus flat–to–channel area ratio β (top row), slope parameter α (middle row), drag coefficient c _d (bottom row) and along–channel variable x^∗ for the M₀ (left column), M₂ (middle column) and M₄ (right column) harmonics. The bold values on the vertical axis represent the default setting, β = 2, α = 1 and c _d = 0.0025. The remaining parameters have the same value as in Table 2

Fig. 5

Contours of the momentum sink–induced amplitude difference ΔAmpl in current velocity versus flat–to–channel area ratio β (top row), slope parameter α (middle row), drag coefficient c _d (bottom row) and along–channel variable x^∗ for the M₂ (left column) and M₄ (right column) harmonics. The bold values on the vertical axis represent the default setting, β = 2, α = 1 and c _d = 0.0025. The remaining parameters have the same value as in Table 2

What stands out in Figs. 4–5 is that ΔAmpl in both the sea surface elevation and current velocity is most sensitive to changes in flat–to–channel area ratio β, and less to changes in slope parameter α and drag coefficient c _d . Figure 4 reveals that the momentum sink lowers the M₂ amplitude and increases the M₄ one for almost all β values considered. Furthermore, it illustrates that ΔAmpl depends nonlinearly on β. In particular, the sensitivity of ΔAmpl to β decreases, as β increases. Figure 5 shows that these conclusions also hold for the current velocity.

Furthermore, Fig. 4 reveals that, although ΔAmpl in M₀ and M₂ are rather insensitive to changes in α, the response of the M₄ harmonic of the sea surface elevation on changing α values is more interesting. On the right side of the embayment, for small α, the momentum sink increases (red colours) the M₄ sea surface elevation amplitude while for larger values of α, the M₄ amplitude is decreased (blue colours). From the bottom panels of Figs. 4–5 it follows that, for smaller values of the drag coefficient, the momentum sink lead to a larger difference in sea surface elevation and current velocity amplitude.

The sensitivity of ΔAmpl in sea surface elevation and current velocity to the embayment length L^∗ and the phase difference 𝜃 between the incoming tidal waves is presented in Figs. 6 and 7. For increasing 𝜃 values, the spatial pattern of ΔAmpl shifts towards the right, and the M₂ and M₄ sea surface elevation amplitude and M₄ current velocity amplitude decreases. Particularly noticeable about the sensitivity of ΔAmpl on L^∗ is that the M₂ sea surface elevation amplitude has a local maximum at L^∗≈ 45 km.

Fig. 6

a Contours of the momentum sink–induced amplitude difference ΔAmpl, of the sea surface elevation versus the phase differences between the incoming tidal waves 𝜃 and along–channel variable x^∗ for the M₀ (left panel), M₂ (middle panel) and M₄ (right panel) harmonic. The bold value on the vertical axis represent the default setting 𝜃 = π/4. The remaining parameters have the same value as in Table 2. b As (a), but for the current velocity u^∗

Fig. 7

As Fig. 6, but for different embayment lengths L^∗. The bold value on the vertical axis represent the default setting L^∗ = 57 km

5 Discussion

5.1 Physical interpretation of the results

In this section, some results obtained in the preceding section are interpreted by analysing the expressions from Section 3. To that end, it is helpful to rewrite term V in the O(ε) problem (22) using the continuity Eq. 14. That term becomes:

$$ \beta u_{0}\frac{\partial \zeta_{0}}{\partial t} \mathscr{H}\left( -\frac{\partial \zeta_{0}}{\partial t}\right) = \frac{-\beta}{1+\beta}u_{0}\frac{\partial u_{0}}{\partial x} \mathscr{H}\left( -\frac{\partial \zeta_{0}}{\partial t}\right). $$

(35)

This shows that the momentum sink is similar to the advection term when the tide falls and, in particular, that the momentum sink term is always smaller than the advection term, by virtue of $\beta /(1+\beta ) = (b_{{\max }}^{\ast }-b_{c}^{\ast })/b_{{\max }}^{\ast } <1$.

The impact of the momentum sink on the residual sea surface elevation becomes apparent by this similarity. In fact, since $\langle \mathscr {H}\left (-\partial \zeta _{0}/\partial t\right )\rangle = 1/2$, integration over one tidal period of the O(ε) momentum Eq. 22 using Eq. 35 results in

$$\begin{array}{@{}rcl@{}} \frac{\partial \langle\zeta_{1}\rangle}{\partial x} &=& -\frac{1}{4}\frac{\partial|\hat{u}_{0}|^{2}}{\partial x}\left( \underbrace{\vphantom{\frac{\beta}{\beta}}1}_{\text{III}} + \underbrace{\frac{\beta}{2(1+\beta)}}_{\mathrm{V}} \right)\\ &&+ \underbrace{|\hat{u}_{0}||\hat{\zeta}_{0}|r\cos(\phi_{\hat{u}_{0}s}- \phi_{\hat{\zeta}_{0}})}_{\text{IV}}. \end{array} $$

(36)

It follows from this expression that the momentum sink increases the absolute value of the gradient of residual sea surface elevation. This clarifies the results in Fig. 2a.

In Section 4, it was found that the momentum sink reduces the amplitude of the M₂ harmonic for most parameter values. To understand why, note that term M^∗ in Eq. 5 (which arises as term V in the O(ε) momentum equation) represents a force per mass unit, as it appears on the right hand side in the dimensional momentum Eq. 4. During the falling tide, this force acts against the direction of the current (as shown in Eq. 35, term V and u₀ have opposite signs when ∂ζ₀/∂t < 0), whilst during the rising of the tide it is inactive (term V is zero). In other words, when the water level drops, stagnant water enters the channel from the flats, thereby slowing the channel current. During the rising of the tide, water flows from the channel onto the flats, which leaves the channel current unaffected. All in all, this implies that term V reduces the current of the principal tidal component. The continuity Eq. 14 implies, in turn, that the same holds for the sea surface elevation.

In a system resembling the Marsdiep–Vlie system, the momentum sink increases the M₄ amplitudes (Fig. 2). This can also be explained using Eq. 35. This equation expresses that the momentum sink term is the product of a constant, the advection term and the step function. The advection term consists of an M₀ and M₄ harmonic and the step function consists of an M₀ and odd harmonics. The M₄ component of the momentum sink is therefore the product of the M₄ harmonic of the advection term and the M₀ harmonic of the step function. That is, the momentum sink generates an M₄ harmonic with the same phase as the M₄ generated by advection (see Appendix B for details). Ridderinkhof et al. (2014) showed that advection leads to stronger and shorter flood currents (flood dominance). The momentum sink therefore also favours flood dominance. Since Fig. 3 shows that the transport of coarse sediment is in the flood direction, it implies that the current is flood dominant. Thus, the M₄ generated by the momentum sink increases the total M₄ current velocity amplitude.

Figure 4 showed that, when the slopes of the flats are small (large α), the M₄ amplitude of the sea surface elevation is decreased by the momentum sink while it is increased for the default value of α. The reason for this is similar to the above. When α is large, the mass storage is the dominant mechanism producing the M₄ overtide in the sea surface elevation. Since this term generates M₄ that is out of phase with the M₄ generated by the momentum sink, including the momentum sink reduces the total M₄ amplitude of the sea surface elevation.

Figure 2 revealed that the amplitudes of the sea surface elevation (and the current velocity) are different at the two boundaries. In these experiments, the amplitudes of the incoming tidal waves are equal, so even then, the resulting amplitudes at the boundaries differ. This is already included in the linear dynamics. The O(1) solution (18)–(20) of the linearised problem yields, if z _l = z _r , that

$$ |\hat{\zeta}_{0}({\kern-.5pt}-{\kern-.5pt}L{\kern-.5pt}/{\kern-.5pt}2)|^{2} {\kern-.5pt}-{\kern-.5pt} |\hat{\zeta}_{0}(L/2)|^{2} {\kern-.5pt}={\kern-.5pt} 4{z_{l}^{2}}e^{-\text{Im}\left\{{k} \right\}L}\sin(\theta){\kern-.5pt}\sin(\text{{\kern-.5pt}Re}{\kern-.5pt}\left\{ {k} {\kern-.5pt}\right\}{\kern-.5pt}L{\kern-.5pt}). $$

(37)

Hence, for equal amplitudes of incoming waves, the amplitude at the boundaries differ when 𝜃 and Re{k(r,β)}L are not a multiple of π, with the difference depending on the phase difference 𝜃, the friction parameter r, the length of the channel L and the flat–to–channel area ratio β. Furthermore, it follows from Eq. 37 that, in a longer embayment, the difference in amplitude due to the phase difference of the incoming tidal waves, becomes smaller. Physically, this makes sense, since in a longer embayment, a wave needs more time to propagate from one side to the other. All this time it is subject to friction. Hence, for large L, $\hat {\zeta }_{0}(\pm L/2)$ is mainly determined by the incoming wave. Figure 8 quantifies the difference $|\hat {\zeta }_{0}(-L/2)| - |\hat {\zeta }_{0}(L/2)|$ between the O(1) sea surface elevation amplitude at the left and right boundary for different flat–to–channel area ratios β and phase differences 𝜃 between the incoming tidal waves. The difference varies between + 10 and − 50 cm and is largest for small β and large 𝜃 values (blue area).

Fig. 8

The difference between the O(1) sea surface elevation amplitude at the left (x = −L/2) and right (x = L/2) boundary versus flat–to–channel area ratio β and phase difference 𝜃 between the tidal waves entering the embayment at the left and right boundary. The remaining parameters have the same value as in Table 2. In particular, the amplitudes z _l and z _r of the incoming tidal waves are equal. The red dot denotes the default value of β and 𝜃

5.2 Model limitations

In this study, the bottom stress is linearised to obtain analytically tractable (linear) O(1) and O(ε) problems. When the M₂ tide is dominant, nonlinear bottom stress is known to especially generate odd overtides M₆, M₁₀,… (Parker 1984). It is possible to include an approximation of the M₆ generated by the nonlinear bottom stress. However, as stated in Friedrichs and Aubrey (1994), one–dimensional numerical models, even with nonlinear bottom stress, simulate observed M₆ variations rather poorly. The authors remark that this might be due to the invalid assumption of a constant drag coefficient c _d . Therefore, as in Friedrichs and Aubrey (1994), the focus of this study is on the primary tide and its first overtide.

In natural tidal embayments, along–channel velocity u is strongly reduced on the flats, but does not vanish completely. The choice of vanishing u on the flats is made to consider the extreme case. As is shown in Section 4, there are (physically relevant) parameter regimes in which the momentum sink generates noticeably overtides. It would be interesting to relax this assumption in a future study.

The trapezoidal cross section is chosen to approximate concave–up tidal flats which typically occur in nature (Friedrichs 2011). The approximation is such that the partly linear flat is tangential to the convex bed at $y^{*}=\pm b^{*}_{{\max }}/2$ and $y^{*} = \pm b^{*}_{c}/2$ (see Fig. 9). In this study, steep slopes and wide flats are chosen to obtain a system in which all nonlinear terms, and in particular both the momentum sink and the mass storage, are O(ε), i.e., β = O(1) and q = O(1/ε). Other choices are possible. For example, Speer and Aubrey (1985) considered moderate slopes and narrow flats, i.e. β = O(ε) and q = O(1). In that case, the momentum sink term is O(ε²) and the mass storage is O(ε).

Fig. 9

The trapezoidal cross section considered in the idealised model (solid line), which is an approximation of the concave–up flats (dashed line)

Furthermore, for simplicity, an embayment with a constant depth and width is chosen. Also, effects of wind, waves, density differences and radiation damping (as in Roos and Schuttelaars 2015) are ignored. These are possible extensions of the model.

5.3 Comparison with results of a complex numerical model

In this section, the results of Section 4 are compared with hydrodynamics simulations of the Dutch Wadden Sea performed using the General Estuarine Transport Model (GETM). GETM is a three–dimensional finite difference model solving the primitive equations and includes a drying and flooding algorithm of the tidal flats. The resolution was 200 m horizontally; there were 30 vertical layers and a realistic bathymetry and forcing (see Duran-Matute et al. (2014) for further details and an extensive comparison with several tidal gauges).

A transect across the Western Wadden Sea is chosen (see Fig. 10a) across which the tidal channels connect the Marsdiep and Vlie inlet (similar as in Ridderinkhof1988). In Fig. 10b, the M₂ and M₄ amplitude of the sea surface elevation in April 2009 (a calm month in terms of wind) along this transect are depicted together with the ones from the idealised model (as in Fig. 2). The magnitude and spatial distribution of the M₂ harmonic of the sea surface elevation as calculated by the idealised model and that of GETM roughly agree. The M₄ amplitude calculated by GETM is approximately four times larger as that calculated by the idealised model. However, when the momentum sink is accounted for, the error becomes smaller (reduction of approximately 7%). A possible explanation for this difference is that, in the idealised model, there is no M₄ harmonic in the tidal wave entering the domain. In GETM, the M₄ amplitude of the sea surface elevation 14 km northwest of Texel is approximately 0.082 m. The dashed-dotted line in Fig. 10b represents the M₄ harmonic of the sea surface elevation when such an M₄ tidal wave entering at the boundaries is imposed. That is, the sea surface elevation of the right–propagating wave at x = −L/2 and the left–propagating wave at x = L/2 are chosen to be, respectively,

$$\begin{array}{@{}rcl@{}} && z_{l}\cos(\text{Re}\left\{ {k} \right\}x-t) + \varepsilon z_{l,2}\cos(\text{Re}\left\{ {k} \right\}x-t) \quad\text{and}\\ &&z_{r}\cos(\text{Re}\left\{ {k} \right\}x+t-\theta) + \varepsilon z_{r,2}\cos(\text{Re}\left\{ {k} \right\}x+t - \theta_{m}), \end{array} $$

with z _l = z _r = z_l,2 = z_r,2 = 0.7 and 𝜃₂ = 0. In that case, the difference between the M₄ amplitude of the idealised model and that of GETM decreases at the boundaries, but increases in the middle of the channel.

Fig. 10

a Transect across the Marsdiep–Vlie inlet systems located in the Western Wadden Sea. Colours indicate the bathymetry used in GETM. b The M₂ and M₄ amplitudes of the sea surface elevation calculated by GETM on this transect (dotted lines). The solid lines are the M₂ and M₄ as in Fig. 2 (including the momentum sink). The dashed-dotted line represents the M₄ harmonic calculated by the idealised model when an external M₄ tidal wave is included in the boundary conditions. The point x^∗ = 0 is located by the red dot in panel (a)

Figure 2 suggests that the amplitude of the sea surface elevation at the Vlie will be higher than at the Marsdiep. This agrees with data presented in the Royal Netherlands Navy (2016) and the results of GETM also demonstrate this behaviour (Fig. 10b). In Section 5.1, it was shown that this amplitude difference is also possible without a difference in the external forcing.

6 Conclusions

The first objective of this study was to assess changes in tidal characteristics of sea surface elevation and current velocity due to the momentum sink in double inlet systems. It is found that the momentum sink decreases the M₂ amplitude of both the current velocity and the sea surface elevation and favours flood dominant tides. In a prototype system, viz. the Marsdiep–Vlie system in the Western Wadden Sea, it implies a decrease of M₂ amplitudes of approximately 2% and an increase of both M₄ amplitudes by 25%. The absolute value of the residual sea surface elevation increased by 30% due to the momentum sink, whereas the residual current velocity was unaffected. The phases of the M₂ tidal harmonic of both sea surface elevation and current velocity were not influenced by the momentum sink; only the M₄ phases were lowered by approximately 10^∘–15^∘. In total, this amounts to an increase of net import of coarse sediment by approximately 35%. Accumulation of coarse sediment was found inside the domain, indicating the formation of a tidal watershed. The transport of fine sediment was hardly influenced.

It is found that the changes in tidal characteristics are most sensitive to the flat–to–channel area ratio. The change in amplitude depends nonlinearly on that ratio; the sensitivity is smaller for larger values of the ratio. Furthermore, it is found that the momentum sinks affects the tidal harmonics of the sea surface elevation and current velocity more strongly when the drag coefficient is small and when the slope of the tidal flats decreases, at the right side of the channel (0 < x < L/2), the sea surface elevation M₄ amplitude does the same. A phase difference between the incoming tidal waves leads to spatial shifts of the curves that show amplitudes and phases versus along–chanel distance and to a small decrease of the M₂ and M₄ amplitudes. Finally, it is found that the difference in M₂ sea surface elevation amplitude due to the momentum sink has a local maximum for a length of the embayment at approximately 45 km.

The second objective was to understand the mechanims behind the changes in tidal characteristics due to the momentum sink. The reduction of the M₂ harmonic amplitude of the sea surface elevation and current velocity by the momentum sink is attributable to that, during the fall of the tide, still water enters the channel and slows down the current. The increase in M₄ amplitude of the sea surface elevation and current velocity is explained by noting that the momentum sink acts as an advective term during the fall of the tide, but with a smaller amplitude. Since advection is known to favour flood currents (e.g. Friedrichs and Aubrey1988; Ridderinkhof et al. 2014), the momentum sink does so as well and increases the M₄ amplitude in a flood dominant system.

A comparison with the complex numerical model GETM showed that the two models produce similar M₂ amplitudes of the sea surface elevation. When the momentum sink is accounted for and an M₄ harmonic is added to the incoming tidal waves, the amplitude of the M₄ harmonic of the sea surface elevation shows a closer resemblance to the one modelled by GETM.

Appendices

Appendix A: Derivation of term M ^∗ in Eq. 4

In this section, the expression for the momentum sink term M^∗ in Eq. 4 is derived. The derivation only concerns dimensional equations and the asterisks are omitted to keep notation as simple as possible. Equations 3–4 follow from integrating the depth averaged shallow water equations over the channel width. The latter equations read

$$ \frac{\partial \zeta}{\partial t} + \frac{\partial(\zeta+h)\bar{u}}{\partial x} + \frac{\partial(\zeta+h)\bar{v}}{\partial y} = 0, $$

(38)

$$ \frac{\partial (\zeta \,+\, h)\bar{u}}{\partial t} + \frac{\partial (\zeta\,+\,h) \bar{u}\bar{u}} {\partial x} + \frac{\partial (\zeta\,+\,h) \bar{u}\bar{v}} {\partial y} = - g(\zeta+h)\frac{\partial \zeta}{\partial x} - \frac{\bar{\tau}_{b}}{\rho}, $$

(39)

where, $\bar {u}$ (ms^− 1) is the depth averaged longitudinal velocity, $\bar {v}$ (ms^− 1) the depth averaged lateral velocity and $\bar {\tau }_{b}$ (Nm^− 2) the bottom stress. Note that ζ does not depend on y.

Integration of Eq. 39 over the constant width of the channel [−b _c /2,b _c /2], using the continuity Eq. 3 and neglecting the stresses $(\bar {u}-u)(\bar {u}-u)$ arising from averaging over the width, yields

$$\begin{array}{@{}rcl@{}} && b_{c}(\zeta+h_{c}) \frac{\partial u}{\partial t} + \underbrace{b_{c} u\frac{\partial \zeta}{\partial t}}_{A} - \underbrace{u b \frac{\partial \zeta}{\partial t}}_{B} + b_{c}(\zeta+h_{c})u \frac{\partial u}{\partial x}\\ && + \underbrace{{\int}_{-b_{c}/2}^{b_{c}/2} \frac{\partial (\zeta+h) \bar{u}\bar{v}} {\partial y} \, dy}_{C} + b_{c}g(\zeta+h_{c})\frac{\partial \zeta}{\partial x} + b_{c}\frac{\tau_{b}}{\rho} = 0,\\ \end{array} $$

(40)

in which u (without the bar) represents the cross-sectionally averaged velocity. Term A arises from integration of the first term in Eq. 39 over the width of the channel and term B from integrating the second term in Eq. 39 and subsequently substituting the continuity Eq. 3. Term C represents the lateral exchange of longitudinal momentum between the channel and the flats, and it equals

$$ C = \left. (\zeta+h) \bar{v}\bar{u} \right\rvert_{y=b_{c}/2} - \left. (\zeta+h) \bar{v}\bar{u} \right\rvert_{y=-b_{c}/2} . $$

(41)

This expression is subsequently rewritten in terms of cross-sectionally averaged velocities. Integration of the continuity Eq. 38 over the right and left flats yields the volume transport (per unit length) through the boundary of the main channel,

$$ \left. (\zeta+h)\bar{v} \right\rvert_{y=\pm b_{c}/2} = \pm\frac{b-b_{c}}{2}\frac{\partial \zeta}{\partial t}. $$

(42)

During the rising of the water level, $\bar {v}$ is positive at y = b _c /2 and along–channel momentum is transferred towards the flats. When the water level falls, water moves from the flats to the main channel. Since the momentum is dissipated on the flats, no along–channel momentum returns to the channel. This motivates the choice

$$ \left. \bar{u} \right\rvert_{y=\pm b_{c}/2} = u\mathscr{H}\left( \frac{\partial \zeta}{\partial t}\right). $$

(43)

Substitution of Eqs. 42–43 in (41) yields

$$ C = (b - b_{c})u\mathscr{H}\left( \frac{\partial \zeta}{\partial t}\right)\frac{\partial \zeta}{\partial t}. $$

(44)

The momentum sink term M as in the main text is now obtained by combining terms A, B and C, using $1-\mathscr {H}(x) = \mathscr {H}(-x)$ and dividing by b _c (ζ + h _c ), which yields

$$M = \frac{A+B+C}{b_{c}(\zeta+h_{c})}=\frac{b - b_{c}}{b_{c}}\frac{\bar{u}}{\zeta+h_{c}}\mathscr{H}\left( -\frac{\partial \zeta}{\partial t}\right)\frac{\partial \zeta}{\partial t}{.} $$

If the momentum sink is neglected ($\left . \bar {u} \right \rvert _{y=\pm b_{c}/2} = u$), then A + B = −C and hence, M = 0.

To frame Eqs. 3–5 in context of previous studies, note that Dronkers (1964) suggested that

$$M = j_{1}\frac{b - b_{c}}{b_{c}}\frac{u}{\zeta+h_{c}}\frac{\partial \zeta}{\partial t},$$

where j₁ = 0 when the water level rises and otherwise depends on the velocities on the flats. Speer and Aubrey (1985) and Friedrichs and Aubrey (1988) assumed the term (b − b _c )/b _c to be small, and M was therefore neglected. Speer (1984) also considered the case with j₁ = 1. In that case, the tidal flats act as momentum storage regions. The choice made in Alebregtse (2015), de Swart et al. (2011) and the current study is $j_{1} = \mathscr {H} \left (-\frac {\partial \zeta }{\partial t}\right )$.

Appendix B: Fourier coefficients of momentum sink term

In the main text term V is written as

$$\beta u_{0}\frac{\partial \zeta_{0}}{\partial t}\mathscr{H}\left( -\frac{\partial \zeta_{0}}{\partial t} \right) = \sum\limits_{m=-\infty}^{\infty} p_{m} e^{-imt}. $$

The Fourier coefficients p _m are

$$\begin{array}{@{}rcl@{}} p_{m} &=& \frac{i\beta}{4} \left( c_{2+m}^{*}\hat{u}_{0}^{*}\hat{\zeta}_{0}^{*} - c_{2-m}\hat{u}_{0}\hat{\zeta}_{0}\right)\\ &&- \frac{\beta}{2}c_{m}^{*}|\hat{u}_{0}||\hat{\zeta}_{0}|\sin(\phi_{\hat{u}_{0}} - \phi_{\hat{\zeta}_{0}}),\end{array} $$

where (in this appendix) ⋅^∗ denotes the complex conjugate and

$$c_{m} = \left\{\begin{array}{ll}\displaystyle \frac{1}{2} & \text{if } m = 0\\\displaystyle 0 & \text{if } m\neq0 \text{ and even}\\\displaystyle \frac{-i}{m\pi}e^{-im\phi_{\hat{\zeta}_{0}}} & \text{if } m \text{ odd}, \end{array}\right.$$

such that

$$ \mathscr{H}\left( -\frac{\partial \zeta_{0}}{\partial t}\right) = \sum\limits_{m=-\infty}^{\infty} c_{m} e^{imt}. $$

(45)

In order to see that the phase of the M₄ harmonic of term V equals that of the advection term, note that term V can be written as a product of a constant, the advection term and the step function as in Eq. 35. From Eqs. 16–20, it follows that the advection term consists of an M₀ and M₄ harmonic,

$$ u_{0}\frac{\partial u_{0}}{\partial x} = A_{M_{0}} + \text{Re}\left\{ {A_{M_{4}}e^{-2it}} \right\}, $$

(46)

where $A_{M_{0}}$ is a real number and $A_{M_{4}}$ a complex number. Since the even Fourier coefficients of the step function c _m are zero, multiplying (46) and (45) yields that the M₄ harmonic of the product equals

$$c_{0}\text{Re}\left\{ {A_{M_{4}}e^{-2it}} \right\}. $$

Hence, the phase of the M₄ harmonic of term V equals $\arg (A_{M_{4}})$ and thus the phase of the M₄ harmonic of the advection term.