A nonlinear elliptic eigenvalue–transmission problem with Neumann boundary condition

Abstract

Let $\varOmega \subset \mathbb {R}^N$, $N\ge 2$, be a bounded domain which is divided into two sub-domains $\varOmega _1$ and $\varOmega _2$. Consider in $\varOmega$ an eigenvalue–transmission problem associated with the p-Laplacian acting in $\varOmega _1$ and the q-Laplacian acting in $\varOmega _2$, $1<p<q$, with Dirichlet–Neumann conditions on the interface separating the two sub-domains $\varOmega _1$ and $\varOmega _2$ [see (1.1)]. The main result Theorem 2.1 states the existence of a sequence of eigenvalues for this eigenvalue problem. The proof is based on the Lusternik–Schnirelmann principle. Using the method of Lagrange multipliers for constrained minimization problems, we show (see Theorem 2.2) that if $2\le p<q$ then there exists an eigenfunction in any set of the form

$$\begin{aligned} \left\{ u\in W^{1,p}(\varOmega );\, u|_{\varOmega _2}\in W^{1,q}(\varOmega _2), \, \frac{1}{p}\int _{\varOmega _1}|u|^p + \frac{1}{q}\int _{\varOmega _2}|u|^q = \alpha \right\} , \quad \alpha >0. \end{aligned}$$

The case of Robin conditions on $\partial \varOmega$ and the Riemannian setting are also addressed.

1 Introduction

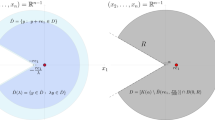
Consider a bounded domain $\varOmega \subset \mathbb {R}^N,~N\ge 2$, with Lipschitz boundary $\partial \varOmega$, which is divided into two Lipschitz sub-domains $\varOmega _1$ and $\varOmega _2$ by a Lipschitz closed hypersurface H. We further assume that $H\cap \partial \varOmega$ is an $(N-2)$-dimensional manifold. In the differentiable category this is the case whenever H and $\partial \varOmega$ intersect transversally. In other words, $\varOmega =\varOmega _1\cup \varOmega _2\cup \varGamma$, where $\varGamma = H\cap \varOmega .$ The standard example we have in mind is the disc $D^N$ divided by some coordinate hyperplane in two open components, i.e. the two open semidiscs. Deformations of this divided disc are a good enough source of further examples. The boundary of $\varOmega$ is assumed smooth enough and is divided into two pieces $\partial \varOmega _1$ and $\partial \varOmega _2$ in such a way that $\partial \varOmega _1$ is the union $\varGamma _1\cup \varGamma$ and $\partial \varOmega _2$ is the union $\varGamma _2\cup \varGamma$. To this picture we consider the eigenvalue problem

$$\begin{aligned} \left\{ \begin{array}{lr} -\varDelta _p u_1=\lambda \mid u_1\mid ^{p-2}u_1\quad \text{ in } ~ \varOmega _1, &{} (1)\\ -\varDelta _q u_2=\lambda \mid u_2\mid ^{q-2}u_2\quad \text{ in } ~ \varOmega _2, &{} (2)\\ \displaystyle \frac{\partial u_1}{\partial \nu _{p}}=0 ~~ \text{ on } ~~\varGamma _1,~ \displaystyle \frac{\partial u_2}{\partial \nu _{q}}=0 ~~ \text{ on } ~~ \varGamma _2, &{} (3)\\ u_1=u_2,~~ \displaystyle \frac{\partial u_1}{\partial \nu _{p}}=\displaystyle \frac{\partial u_2}{\partial \nu _{q}}~~ \text{ on } ~ \varGamma , &{} (4) \end{array}\right. \end{aligned}$$

(1.1)

where $\varDelta _r$ stands for the r-Laplace operator, namely $\varDelta _r w:=\text{ div }\big ( \mid \nabla w\mid ^{r-2} \nabla w\big )$ and $\displaystyle \frac{\partial }{\partial \nu _{r}}$ denotes the boundary operator defined by

$$\begin{aligned} \displaystyle \frac{\partial w}{\partial \nu _{r}}:=\mid \nabla w\mid ^{r-2}\displaystyle \frac{\partial w}{\partial \nu }\quad \text{ for } r=p,q,~1<p<q. \end{aligned}$$

The solution $u=(u_1,u_2)$ of the problem (1.1) is understood in a weak sense, i.e. u is an element of the space

$$\begin{aligned} W:=\big \{u\in W^{1,p}(\varOmega ) : u\vert _{\varOmega _2}\in W^{1,q}(\varOmega _2)\big \}, \end{aligned}$$

(1.2)

where $u_i=u|_{\varOmega _i}$ satisfies the nonlinear problem (1.1)$_i$ on $\varOmega _i$ in the sense of distributions, $i=1,2$, and $u_1$, $u_2$ satisfy the boundary and transmission conditions (1.1)$_{3,4}$ in the sense of traces. Recall that, for any domain $\hat{\varOmega } \subset \mathbb {R}^N$ with Lipschitz boundary $\partial \hat{\varOmega }$, the trace operator

$$\begin{aligned} Tr^{\hat{\varOmega }} : W^{1,p}(\hat{\varOmega }) \rightarrow W^{1-1/p,p}(\partial \hat{\varOmega }) \end{aligned}$$

is a linear and bounded operator, for $1\le p < \infty$ (see Gagliardo [8]). For linear transmission problems, involving the Laplace operator or some perturbed Stokes operators, treated by using the layer potential technique, we refer the reader to [5, 9], respectively.

Definition 1.1

A scalar $\lambda \in \mathbb {R}$ is said to be an eigenvalue of the problem (1.1) whenever (1.1) admits a nontrivial solution $u=(u_1,u_2)\in W$. In that case $u=(u_1,u_2)$ is called an eigenfunction/eigencouple of the problem (1.1) (which corresponds to the eigenvalue $\lambda$) and the pair $(u,\lambda )$ an eigenpair of the problem (1.1). Note that $W^{1,q}(\varOmega )$ is a subspace of W, as $W^{1,q}(\varOmega )$ is a subspace of $W^{1,p}(\varOmega )$.

We endow W with the norm

$$\begin{aligned} \parallel u\parallel _W:=\parallel u\vert _{\varOmega _1}\parallel _{{W^{1,p}(\varOmega _1)}}+\parallel u\vert _{\varOmega _2}\parallel _{{W^{1,q}(\varOmega _2)}},\quad \forall ~u\in W, \end{aligned}$$

where $\parallel \cdot \parallel _{W^{1,p}(\varOmega _1)}$ and $\parallel \cdot \parallel _{W^{1,q}(\varOmega _2)}$ are the usual norms of the Sobolev spaces $W^{1,p}(\varOmega _1)$ and $W^{1,q}(\varOmega _2)$, respectively.

Remark 1.1

The space W defined before can be identified with the space

$$\begin{aligned} \widetilde{W}:=\left\{ (u_1,u_2)\in W^{1,p}(\varOmega _1)\times W^{1,q}(\varOmega _2); \,\, \text{ Tr }^{\varOmega _1}u_1=~\text{ Tr }^{\varOmega _2}u_2~~\text{ on }~\varGamma \right\} , \end{aligned}$$

(1.3)

which shows that W is a reflexive Banach space, as $\tilde{W}$ is a closed subspace of the reflexive product $W^{1,p}(\varOmega _1)\times W^{1,q}(\varOmega _2)$ with reflexive factors.

While the inclusion $W\subseteq \widetilde{W}$ is obvious, for the opposite one we consider $(u_1, u_2) \in \widetilde{W}$ and define

$$\begin{aligned} u(x)= \left\{ \begin{array}{l} u_1(x),\quad x\in \varOmega _1,\\ u_2(x),\quad x\in \varOmega _2. \end{array}\right. \end{aligned}$$

Let us show that $u\in W.$ Obviously, u belongs to $L^p(\varOmega ),$ and its (distributional) derivatives verify the equalities:

$$\begin{aligned} \Big \langle \displaystyle \frac{\partial u}{\partial x_i}, \varphi \Big \rangle= & {} -\Big \langle u, \displaystyle \frac{\partial \varphi }{\partial x_i}\Big \rangle = -\int _{\varOmega _1\cup \varOmega _2} u \displaystyle \frac{\partial \varphi }{\partial x_i}~\hbox {d}x\\= & {} \int _{\varOmega _1} \displaystyle \frac{\partial u}{\partial x_i} \varphi ~\hbox {d}x-\int _{\partial \varOmega _1} u \nu _{1i} \varphi ~\hbox {d}\sigma +\int _{\varOmega _2} \displaystyle \frac{\partial u}{\partial x_i} \varphi ~\hbox {d}x -\int _{\partial \varOmega _2} u \nu _{2i} \varphi ~\hbox {d}\sigma , \end{aligned}$$

for all $\varphi \in C_0^{\infty }(\varOmega )$, where $\nu _1=(\nu _{11},\ldots ,\nu _{1n})$ and $\nu _2=(\nu _{21},\ldots ,\nu _{2n})$ are the outward pointing unit normal fields to boundaries $\partial \varOmega _1$ and $\partial \varOmega _2$, respectively. Clearly, the integral terms on the two boundaries cancel each other as $u_1=u_2$ and $\nu _{1i}+\nu _{2i}=0,~\forall ~i=\overline{1,n},$ on $\varGamma$. Thus,

$$\begin{aligned} \Big \langle \displaystyle \frac{\partial u}{\partial x_i}, \varphi \Big \rangle = \int _{\varOmega _1} \displaystyle \frac{\partial u}{\partial x_i} \varphi ~\hbox {d}x+\int _{\varOmega _2} \displaystyle \frac{\partial u}{\partial x_i} \varphi ~\hbox {d}x, \quad \forall \ \varphi \in C_0^{\infty }(\varOmega ), \end{aligned}$$

which shows that

$$\begin{aligned} \displaystyle \frac{\partial u}{\partial x_i}\Big |_{\varOmega _1}=\displaystyle \frac{\partial u_1}{\partial x_i}\, \text{ and } \, \displaystyle \frac{\partial u}{\partial x_i}\Big |_{\varOmega _2}=\displaystyle \frac{\partial u_2}{\partial x_i}, \end{aligned}$$

for all $i=\overline{1,n}$, and the desired claim follows now easily.

Proposition 1.1

The scalar $\lambda \in \mathbb {R}$ is an eigenvalue of the problem (1.1) if and only if there exists $u=u_\lambda \in W {\setminus } \{0\}$ such that

$$\begin{aligned}&\int _{\varOmega _1} \mid \nabla u\mid ^{p-2}\nabla u\cdot \nabla w~\hbox {d}x+\int _{\varOmega _2}\mid \nabla u\mid ^{q-2}\nabla u \cdot \nabla w~\hbox {d}x \nonumber \\&\quad =\lambda \Big (\int _{\varOmega _1} \mid u\mid ^{p-2} u w~\hbox {d}x+\int _{\varOmega _2} \mid u\mid ^{q-2} u w~\hbox {d}x\Big ),\quad \forall ~ w\in W. \end{aligned}$$

(1.4)

Proof

Indeed, if $u\in W$ is a solution of the problem (1.1), then we have for all $w\in W$

$$\begin{aligned}&\displaystyle \int _{\varOmega _1}\mathrm{div}\left( |\nabla u|^{p-2}\nabla u\right) w~\hbox {d}x+ \displaystyle \int _{\varOmega _2}\mathrm{div} \left( |\nabla u|^{q-2}\nabla u\right) w~\hbox {d}x\\&\quad =-\lambda \displaystyle \int _{\varOmega _1}|u|^{p-2} u w ~\hbox {d}x- \lambda \displaystyle \int _{\varOmega _2}|u|^{q-2} u w~\hbox {d}x \end{aligned}$$

or, equivalently,

$$\begin{aligned}&-\displaystyle \int _{\varOmega _1}|\nabla u|^{p-2}\nabla u\cdot \nabla w~\hbox {d}x+ \displaystyle \int _{\varGamma } w|\nabla u|^{p-2}\displaystyle \displaystyle \frac{\partial u}{\partial \nu } ~\hbox {d}\sigma - \displaystyle \int _{\varOmega _2}|\nabla u|^{q-2}\nabla u\cdot \nabla w~\hbox {d}x\\&\quad - \displaystyle \int _{\varGamma } w|\nabla u|^{q-2}\displaystyle \displaystyle \frac{\partial u}{\partial \nu }~\hbox {d}\sigma =-\lambda \displaystyle \int _{\varOmega _1}|u|^{p-2} u w ~\hbox {d}x- \lambda \displaystyle \int _{\varOmega _2}|u|^{q-2} u w~\hbox {d}x, \end{aligned}$$

which is equivalent to (1.4).

Conversely, assume that $u \in W$ satisfies (1.4) and consider $w\in W$ such that $w\vert _{\varOmega _1}=\varphi$ for some arbitrary $\varphi \in C_0^\infty (\varOmega _1)$ and $w\vert _{\varOmega _2}=0.$ We obtain

$$\begin{aligned} \int _{\varOmega _1} \mid \nabla u\mid ^{p-2}\nabla u \cdot \nabla \varphi ~\hbox {d}x=\lambda \int _{\varOmega _1} \mid u\mid ^{p-2} u \varphi ~\hbox {d}x,\quad \forall ~\varphi \in C_0^\infty (\varOmega _1). \end{aligned}$$

By using the formula of integration by parts, we obtain

$$\begin{aligned} -\int _{\varOmega _1} \text{ div }\big ( \mid \nabla u\mid ^{p-2} \nabla u\big ) \varphi ~\hbox {d}x=\lambda \int _{\varOmega _1} \mid u\mid ^{p-2} u \varphi ~\hbox {d}x,\quad \forall ~\varphi \in C_0^\infty (\varOmega _1), \end{aligned}$$

which shows that $-\varDelta _p u=\lambda \mid u\mid ^{p-2}u$ in $\varOmega _1.$ Similarly, $-\varDelta _q u=\lambda \mid u\mid ^{q-2}u$ in $\varOmega _2.$

We next assume that $w\in C^1(\overline{\varOmega })$ and $w\vert _{\varOmega _2}=0.$ With such a choice of w, using the integration by parts formula, the fact that $w\vert _{\varGamma }=0$ and the equation $-\varDelta _p u=\lambda \mid u\mid ^{p-2}u$ in $\varOmega _1$ obtained above, the relation (1.4) implies

$$\begin{aligned} 0=\int _{\partial \varOmega _1} w \mid \nabla u\mid ^{p-2}\displaystyle \frac{\partial u}{\partial \nu } ~\hbox {d}\sigma =\int _{\varGamma _1} w \mid \nabla u\mid ^{p-2}\displaystyle \frac{\partial u}{\partial \nu } ~\hbox {d}\sigma \end{aligned}$$

for all $w\in C^1(\overline{\varOmega }_1),~ w\vert _{\varGamma }=0$, therefore $\displaystyle \frac{\partial u}{\partial \nu _p}=\mid \nabla u\mid ^{p-2}\displaystyle \frac{\partial u}{\partial \nu }=0$ on $\varGamma _1.$ One can similarly show that $\displaystyle \frac{\partial u}{\partial \nu _q}=\mid \nabla u\mid ^{q-2}\displaystyle \frac{\partial u}{\partial \nu }=0$ on $\varGamma _2.$

It remains to obtain the transmission conditions on $\varGamma$. First of all, it is obvious that $\text{ Tr }^{\varOmega _1}(u\vert _{\varOmega _1})= \text{ Tr }^{\varOmega _2}(u\vert _{\varOmega _2})$ on $\varGamma$. Finally, we take in (1.4) $w=\varphi$, where $\varphi$ is an arbitrary function in $C_0^\infty (\varOmega )$. Using again the integration by parts formula (in particular, on $\varGamma$ we have $\nu _1+\nu _2=0,$ the normal vector $\nu _k$ being chosen to point towards the exterior of $\varOmega _k, k=1,2$) and the equations and equalities proved before, we derive

$$\begin{aligned} \int _{\varGamma } \varphi \displaystyle \frac{\partial u}{\partial \nu _p} ~\hbox {d}\sigma +\int _{\varGamma } \varphi \displaystyle \frac{\partial u}{\partial \nu _q} ~\hbox {d}\sigma =0,\quad \forall ~\varphi \in C_0^\infty (\varOmega ). \end{aligned}$$

Thus, the transmission relation

$$\begin{aligned} \displaystyle \frac{\partial u}{\partial \nu _p}= \displaystyle \frac{\partial u}{\partial \nu _q}~~ \text{ on } ~ \varGamma \end{aligned}$$

is satisfied. This completes the proof. $\square$

If we choose $w=u$ in (1.4), we see that there exist no negative eigenvalues of problem (1.1). It is also obvious that $\lambda _0=0$ is an eigenvalue of this problem and the corresponding eigenfunctions are the nonzero constant functions. So any other eigenvalue belongs to $(0,\infty )$.

Obviously, u corresponding to any eigenvalue $\lambda >0$ cannot be a constant function (see (1.4) with $w=u$).

If we assume that $\lambda >0$ is an eigenvalue of problem (1.1) and choose $w\equiv 1$ in (1.4), we deduce that every eigenfunction u corresponding to $\lambda$ satisfies the equation

$$\begin{aligned} \int _{\varOmega _1} \mid u\mid ^{p-2} u ~\hbox {d}x+\int _{\varOmega _2} \mid u\mid ^{q-2} u ~\hbox {d}x=0. \end{aligned}$$

So all eigenfunctions corresponding to positive eigenvalues necessarily belong to the set

$$\begin{aligned} \mathscr {C}:=\Big \{ u\in W;~\int _{\varOmega _1} \mid u\mid ^{p-2} u ~\hbox {d}x+\int _{\varOmega _2} \mid u\mid ^{q-2} u ~\hbox {d}x=0\Big \}. \end{aligned}$$

(1.5)

Using the Sobolev’s embedding theorem and [11, Lemma $A_1$]), we can see that $\mathscr {C}$ is a weakly closed subset of W. This set has nonzero elements. To show this, we choose $x_1, x_2\in \varOmega _1,~ x_1\ne x_2$, $r>0$, such that $B_r(x_1)\cap B_r(x_2)=\emptyset ,~B_r(x_k)\subset \varOmega _1$, and consider the test functions $u_k: \varOmega \rightarrow \mathbb {R}, \, k=1,2,$

$$\begin{aligned} u_k(x)= \left\{ \begin{array}{ll} e^{-\displaystyle \frac{1}{r^2-\mid x-x_k\mid ^2}},&{}\quad \text{ if }~x\in B_r(x_k),\\ 0, &{}\quad \text{ otherwise. } \end{array}\right. \end{aligned}$$

Clearly, $u_k\in W$, $k=1,2$. Denote

$$\begin{aligned} \theta _k=\int _{\varOmega } u_k ^{p-1} ~\hbox {d}x. \end{aligned}$$

Obviously, $\theta _k>0$, $k=1,2$. Define $\sigma _k=\theta _k^{\frac{-1}{p-1}},~~ k=1,2$. It is then easily seen that the function $w=\sigma _1 u_1-\sigma _2 u_2$ belongs to $\mathscr {C}{\setminus } \{0\}$.

Our next goal is to prove, via the Lusternik–Schnirelmann principle, that there exists a sequence of positive eigenvalues of problem (1.1). Note, however, that this sequence might not cover the whole eigenvalue set.

2 Results

In what follows we make use of a version of Lusternik–Schnirelmann principle (see [2, 19, Section 44.5, Remark 44.23] and [11]) in order to establish the existence of a sequence of eigenvalues for problem (1.1).

Define the functionals $F,G:W\longrightarrow \mathbb {R}$ by

$$\begin{aligned} F(u):=&\displaystyle \frac{1}{p}\int _{\varOmega _1} \mid u\mid ^{p}\hbox {d}x+\displaystyle \frac{1}{q}\int _{\varOmega _2} \mid u\mid ^{q} \hbox {d}x, \end{aligned}$$

(2.1)

$$\begin{aligned} G(u)&:= \displaystyle \frac{1}{p}\int _{\varOmega _1}\big ( \mid \nabla u\mid ^{p} +\mid u\mid ^{p}\big ) ~\hbox {d}x+\displaystyle \frac{1}{q}\int _{\varOmega _2}\big ( \mid \nabla u\mid ^{q}+ \mid u\mid ^{q}\big ) ~\hbox {d}x\nonumber \\&= F(u)+\displaystyle \frac{1}{p}\int _{\varOmega _1}\mid \nabla u\mid ^{p} ~\hbox {d}x+\displaystyle \frac{1}{q}\int _{\varOmega _2}\mid \nabla u\mid ^{q}~\hbox {d}x. \end{aligned}$$

(2.2)

It is easily seen that functionals F and G are of class $C^1$ on W (see Remark 2.1) and obviously F, G are even with $F(0)=G(0)=0$. We also have

$$\begin{aligned} \langle F'(u), w\rangle =&\int _{\varOmega _1} \mid u\mid ^{p-2}u w ~\hbox {d}x+\int _{\varOmega _2} \mid u\mid ^{q-2}u w ~\hbox {d}x, \end{aligned}$$

(2.3)

$$\begin{aligned} \langle G'(u), w\rangle =&\langle F'(u), w\rangle + \int _{\varOmega _1} \mid \nabla u\mid ^{p-2}\nabla u \cdot \nabla w ~\hbox {d}x + \int _{\varOmega _2} \mid \nabla u\mid ^{q-2} \nabla u \cdot \nabla w ~\hbox {d}x, \end{aligned}$$

(2.4)

for all $w\in W$. We denote by $S_G(1)$ the level set of G,  $S_G(1):=\{u\in W;~G(u)=1\}.$

We have the following auxiliary result:

Lemma 2.1

The functionals F and G satisfy the following properties:

$(h_1)$ :

$F'$ is strongly continuous, i.e. $u_n \rightharpoonup u$ (meaning $u_n \rightarrow u$ weakly) in W$\Rightarrow F'(u_n)\rightarrow F'(u)$ and

$$\begin{aligned} \langle F'(u),u\rangle =0 \Rightarrow u=0; \end{aligned}$$

$(h_2)$ :

$G'$ is bounded and satisfies condition $(S_0),$ i. e.,

$$\begin{aligned} u_n\rightharpoonup u,~G'(u_n)\rightharpoonup w, ~\langle G'(u_n), u_n\rangle \rightarrow \langle w, u\rangle ~\Rightarrow ~u_n\rightarrow u; \end{aligned}$$

$(h_3)$ :

$S_G(1)$ is bounded and if $u\ne 0$ then

$$\begin{aligned} \langle G'(u), u\rangle>0,~~\lim _{t\rightarrow \infty }G(tu)=\infty ,~\inf _{u\in S_G(1)}\langle G'(u), u\rangle >0. \end{aligned}$$

Proof

$(h_1)$ Assume that $u_n\rightharpoonup u$ in W. Hölder’s inequality yields

$$\begin{aligned} \mid \langle F'(u_n)- F'(u), w\rangle \mid\le & {} \parallel \mid u_n\mid ^{p-2}u_n- \mid u\mid ^{p-2}u\parallel _{L^{\frac{p}{p-1}}(\varOmega _1)} \parallel w\parallel _{L^{p}(\varOmega _1)}\nonumber \\&+\parallel \mid u_n\mid ^{q-2}u_n-\mid u\mid ^{q-2}u\parallel _{L^{\frac{q}{q-1}}(\varOmega _2)}\parallel w\parallel _{L^{q}(\varOmega _2)}\nonumber \\\le & {} \left( \parallel \mid u_n\mid ^{p-2}u_n-\mid u\mid ^{p-2}u\parallel _{L^{\frac{p}{p-1}}(\varOmega _1)}\right. \nonumber \\&\left. +\,\parallel \mid u_n\mid ^{q-2}u_n-\mid u\mid ^{q-2}u\parallel _{L^{\frac{q}{q-1}}(\varOmega _2)}\right) \parallel w\parallel _{W}, \end{aligned}$$

(2.5)

for all $w\in W$. This shows that the linear functionals $F'(u_n)-F'(u)$ are all bounded and

$$\begin{aligned} \Vert F'(u_n)- F'(u)&\Vert \le \parallel \mid u_n\mid ^{p-2}u_n-\mid u\mid ^{p-2}u\parallel _{L^{\frac{p}{p-1}}(\varOmega _1)}\nonumber \\&+ \parallel \mid u_n\mid ^{q-2}u_n-\mid u\mid ^{q-2}u\parallel _{L^{\frac{q}{q-1}}(\varOmega _2)}, \end{aligned}$$

(2.6)

for all $n\ge 1$. Since $u_n\rightharpoonup u$ in W, it follows that $\{u_n\}$ as well as the sequences of restrictions $\{u_n\big |_{\varOmega _1}\}$ and $\{u_n\big |_{\varOmega _2}\}$ are bounded (see [1, Proposition 3.5, p. 58]). Consequently, $u_n\rightarrow u$ in $L^p(\varOmega )$, $u_n\vert _{\varOmega _1}\rightarrow u\vert _{\varOmega _1}$ in $L^p(\varOmega _1)$ and $u_n\vert _{\varOmega _2}\rightarrow u\vert _{\varOmega _2}$ in $L^q(\varOmega _2)$, as the canonical injections $W^{1,p}(\varOmega )\hookrightarrow L^p(\varOmega )$, $W^{1,p}(\varOmega _1)\hookrightarrow L^p(\varOmega _1)$ and $W^{1,q}(\varOmega _2)\hookrightarrow L^q(\varOmega _2)$ are all compact (see [20, Proposition 21.29, p. 262]). The convergence $\Vert u_n\Vert _{L^p(\varOmega _1)}\longrightarrow \Vert u\Vert _{L^p(\varOmega _1)}$ is equivalent with

$$\begin{aligned} \int _{\varOmega _1}|\mid u_n\mid ^{p-2}u_n|^{\frac{p}{p-1}}~\hbox {d}x\rightarrow \int _{\varOmega _1}|\mid u\mid ^{p-2}u|^{\frac{p}{p-1}}~\hbox {d}x. \end{aligned}$$

(2.7)

As the set of weak cluster points of the sequence $\{\mid u_n\mid ^{p-2}u_n\}$ in $L^{p/(p-1)}(\varOmega _1)$ is the singleton $\{\mid u\mid ^{p-2}u \}$, it follows that in fact this sequence is strongly convergent in $L^{p/(p-1)}(\varOmega _1)$ to $\mid u\mid ^{p-2}u$ (see, for example, [1, Prop. 3.32, p. 78]).

One can similarly show that $\mid u_n\mid ^{q-2}u_n \rightarrow \mid u\mid ^{q-2}u$ in $L^{q/(q-1)}(\varOmega _2)$. Thus, the convergence $F'(u_n)\rightarrow F'(u)$ in $W^*$ follows by using (2.6).

If $\langle F'(u),u\rangle =0$ then obviously $u=0$.

Note that the strong continuity of G can be similarly derived.

$(h_2)$ Let us first prove that for all $u, w\in W$ the following relations hold:

$$\begin{aligned}&\langle G'(u)-G'( w),u- w\rangle \nonumber \\&\quad \ge \big (\parallel u_1\parallel ^{p-1}_{W^{1,p}(\varOmega _1)}-\parallel w_1\parallel ^{p-1}_{W^{1,p}(\varOmega _1)}\big ) \big (\parallel u_1\parallel _{W^{1,p}(\varOmega _1)}-\parallel w_1\parallel _{W^{1,p}(\varOmega _1)}\big )\nonumber \\&\qquad +\big (\parallel u_2\parallel ^{q-1}_{W^{1,q}(\varOmega _2)}-\parallel w_2\parallel ^{q-1}_{W^{1,q}(\varOmega _2)}\big ) \big (\parallel u_2\parallel _{W^{1,q}(\varOmega _2)}-\parallel w_2\parallel _{W^{1,q}(\varOmega _2)}\big )\ge 0, \end{aligned}$$

(2.8)

where $u_1, w_1,u_2, w_2$ stand for $u\big |_{\varOmega _1}, w\big |_{\varOmega _1},u\big |_{\varOmega _2}, w\big |_{\varOmega _2}$, respectively. Moreover,

$$\begin{aligned} \langle G'(u)-G'( w),u- w\rangle =0~\Leftrightarrow ~u= w~\text{ a. } \text{ e. } \text{ in }~\varOmega . \end{aligned}$$

(2.9)

It is obvious that

$$\begin{aligned} \langle G'(u) - G'( w),u- w\rangle= & {} \parallel u_1 \parallel ^{p}_{W^{1,p}(\varOmega _1)}+\parallel w_1 \parallel ^{p}_{W^{1,p}(\varOmega _1)}\nonumber \\&+ \parallel u_2\parallel ^{q}_{W^{1,q}(\varOmega _2)} +\parallel w_2\parallel ^{q}_{W^{1,q}(\varOmega _2)}\nonumber \\&-\,(T_1+T_2)-(T_3+T_4), \end{aligned}$$

(2.10)

where we have denoted

$$\begin{aligned} T_1:=&\int _{\varOmega _1}\big (\mid \nabla u\mid ^{p-2}\nabla u\cdot \nabla w+\mid u\mid ^{p-2} u w\big )~\hbox {d}x,\\ T_2:=&\int _{\varOmega _1}\big (\mid \nabla w\mid ^{p-2}\nabla w \cdot \nabla u+\mid w\mid ^{p-2} w u\big )~\hbox {d}x, \end{aligned}$$

and $T_3, T_4$ are similarly defined, by replacing p and $\varOmega _1$ with q and $\varOmega _2$. Using the Hölder inequality, we obtain that

$$\begin{aligned} T_1&\le \Big (\int _{\varOmega _1}\mid \nabla u\mid ^p \hbox {d}x \Big )^{\frac{p-1}{p}}\Big (\int _{\varOmega _1}\mid \nabla w\mid ^p \hbox {d}x \Big )^{\frac{1}{p}}+ \Big (\int _{\varOmega _1}\mid u\mid ^p \hbox {d}x\Big )^{\frac{p-1}{p}}\Big (\int _{\varOmega _1}\mid w\mid ^p \hbox {d}x \Big )^{\frac{1}{p}}\nonumber \\&\le \Big (\int _{\varOmega _1}(\mid \nabla u\mid ^p +\mid u\mid ^p) \hbox {d}x \Big )^{\frac{p-1}{p}}\Big (\int _{\varOmega _1}(\mid \nabla w\mid ^p+\mid w\mid ^p) \hbox {d}x \Big )^{\frac{1}{p}}\nonumber \\&= {\parallel u_1\parallel _{W^{1,p}(\varOmega _1)}^{p-1}} \parallel w_1\parallel _{W^{1,p}(\varOmega _1)}, \end{aligned}$$

(2.11)

where we have also used the inequality

$$\begin{aligned} \alpha ^s\gamma ^{1-s}+\beta ^s\delta ^{1-s}\le (\alpha +\beta )^s(\gamma +\delta )^{1-s},\quad \forall ~\alpha , \beta , \gamma , \delta >0,~s\in (0,1). \end{aligned}$$

Similar inequalities can be obtained for the other terms, $T_2, T_3, T_4,$ and using (2.10) we derive (2.8).

Now by (2.8) we see that $\langle G'(u)-G'( w),u- w\rangle =0$ implies

$$\begin{aligned} \parallel u_1\parallel _{W^{1,p}(\varOmega _1)}=\parallel w_1\parallel _{W^{1,p}(\varOmega _1)}, \parallel u_2\parallel _{W^{1,q}(\varOmega _2)}= \parallel w_2\parallel _{W^{1,q}(\varOmega _2)}, \end{aligned}$$

(2.12)

and also we have equalities in Hölder inequalities; therefore, there exist positive constants, $k_1, k_2$ such that $\mid u_i\mid =k_i\mid w_i\mid ,~i=1,2$. On the other hand, we have equality in (2.11); thus,

$$\begin{aligned} T_1=k_1^{p-1}\parallel w_1\parallel _{W^{1,p}(\varOmega _1)}^{p}\Rightarrow u_1=k_1 w_1\,~\text{ a. } \text{ e. } \text{ in }~\varOmega _1. \end{aligned}$$

Similarly, we can derive that $u_2=k_2 w_2~\text{ a. } \text{ e. } \text{ in }~\varOmega _2$ and taking into account (2.12) we derive (2.9).

In order to prove that $G'$ is bounded, we can use again the Hölder inequality and straightforward computations lead us to

$$\begin{aligned} \mid \langle G'(u), w\rangle \mid \le \big (\parallel u_1\parallel _{W^{1,p}(\varOmega _1)}^{p-1} +\parallel u_2\parallel _{W^{1,q}(\varOmega _2)}^{q-1}\big ) \parallel w\parallel _W,\quad \forall ~u, w\in W. \end{aligned}$$

Moreover, a similar argument to the one we used to prove $(h_1)$ would imply the continuity of $G'$.

Finally, let us prove that $G'$ verifies condition $(S_0),$ i.e.,

$$\begin{aligned} u_n\rightharpoonup u,~G'(u_n)\rightharpoonup w, ~\langle G'(u_n), u_n\rangle \rightarrow \langle w, u\rangle ~\text{ implies }~u_n\rightarrow u, \end{aligned}$$

for some $u\in W,~ w\in W^*.$ Indeed, as $u_n\rightharpoonup u$ in W,  we have $u_n\vert _{\varOmega _1}\rightarrow u\vert _{\varOmega _1}$ in $L^p(\varOmega _1)$ and $u_n\vert _{\varOmega _2}\rightarrow u\vert _{\varOmega _2}$ in $L^q(\varOmega _2).$ Since W is a reflexive Banach space, using the Lindenstrauss–Asplund–Troyanski theorem (see [18]), it is enough to prove that $\parallel u_n\parallel _W\rightarrow \parallel u\parallel _W$ in order to obtain the strong convergence $u_n\rightarrow u.$ This convergence is a simple consequence of the equality

$$\begin{aligned} \lim _{n\rightarrow \infty }\langle G'(u_n)-G'(u),u_n-u\rangle =\lim _{n\rightarrow \infty }\big (\langle G'(u_n),u_n\rangle -\langle G'(u_n),u\rangle -\langle G'(u),u_n-u\rangle \big )=0 \end{aligned}$$

and the inequality (2.8).

The properties $(h_3)$ follow immediately from the definition of the functional G. Thus, the proof is complete. $\square$

Remark 2.1

For the convenience of the reader, we recall that:

• 1. the $C^1$-smooth regularity of the functionals F and G follows by computing the Gâteaux derivatives

  $$\begin{aligned} \langle F'(u), w\rangle =\frac{d}{dt}\Big |_{t=0}F(u+t w)\, \text{ and } \, \langle G'(u), w\rangle =\frac{d}{dt}\Big |_{t=0}G(u+t w) \end{aligned}$$

  of F and G at $u\in W$ in the direction $w\in W$ and showing that they have the forms (2.3) and (2.4), respectively. The existence of the Gâteaux derivatives of F and G at every point of W and all directions of W combined with the strong continuity of $F'$ and $G'$ shows the Fréchet differentiability of F and G and therefore the $C^1$-smooth regularity of F and G.

• 2. The weak closedness of the set $\mathscr {C}$ defined by (1.5) follows also from the strong continuity of $F'$ and the representation of $\mathscr {C}$ as $\{u\in W \ | \ \langle F'(u),1\rangle =0\}$.

Due to the properties $(h_1)-(h_3)$, verified by the functionals F and G, combined with their properties to be even and to vanish at zero, it follows, according to the Lusternik–Schnirelmann principle, that the eigenvalue problem

$$\begin{aligned} F'(u)=\mu G'(u),\quad u\in S_G(1) \end{aligned}$$

(2.13)

admits a sequence of eigenpairs $\{(u_n ,\mu _n )\}$ such that $u_n \rightharpoonup 0$ and $\mu _n\longrightarrow 0$ as $n\longrightarrow \infty$ and $\mu _n\ne 0$, for all n. In fact, $\{\mu _n\}$ is a decreasing sequence of non-negative reals (which converges to zero) and

$$\begin{aligned} \mu _n=\sup _{H\in \mathbb {A}_n}\inf _{u\in H} F(u),\quad \forall ~n\in \mathbb {N}, \end{aligned}$$

(2.14)

where $\mathbb {A}_n$ is the class of all compact, symmetric subsets K of $S_G(1)$ such that $F(u)>0$ on K and $\gamma (K)\ge n,$ where $\gamma (K)$ denotes the genus of K, i.e.,

$$\begin{aligned} \gamma (K):=\inf \{ k\in \mathbb {N};~\exists ~h:K\rightarrow \mathbb {R}^k{\setminus }\{0\} \,\text{ such } \text{ that } \text{ h } \text{ is } \text{ continuous } \text{ and } \text{ odd }\}. \end{aligned}$$

The problem (2.13) consists in finding $u\in S_G(1)$ such that

$$\begin{aligned}&\int _{\varOmega _1} \mid u\mid ^{p-2}u w ~\hbox {d}x+\int _{\varOmega _2} \mid u\mid ^{q-2}u w ~\hbox {d}x\\&\quad =\mu \Big (\langle F'(u), w\rangle +\int _{\varOmega _1} \mid \nabla u\mid ^{p-2}\nabla u \cdot \nabla w~\hbox {d}x+\int _{\varOmega _2} \mid \nabla u\mid ^{q-2} \nabla u \cdot \nabla w ~\hbox {d}x\Big ), \end{aligned}$$

for all $w\in W$, or equivalently, in finding $u\in S_G(1),$ such that

$$\begin{aligned}&\int _{\varOmega _1} \mid \nabla u\mid ^{p-2}\nabla u \cdot \nabla w~\hbox {d}x+\int _{\varOmega _2}\mid \nabla u\mid ^{q-2}\nabla u \cdot \nabla w~\hbox {d}x \nonumber \\&\quad =(1/\mu -1)\Big (\int _{\varOmega _1} \mid u\mid ^{p-2} u w~\hbox {d}x+\int _{\varOmega _2} \mid u\mid ^{q-2} u w~\hbox {d}x\Big ),\quad \forall ~ w\in W. \end{aligned}$$

(2.15)

Observe that (2.15) is the variational formulation of problem (1.1). We therefore get the following consequence of the Lusternik–Schnirelmann principle associated with the transmission problem (1.1):

Theorem 2.1

The sequence $\{\mu _n\}$ of eigenvalues of the problem (2.13) produces a nondecreasing sequence $\lambda _n=\displaystyle \frac{1}{\mu _n}-1$ of eigenvalues of the problem (1.1) and obviously $\lambda _n\rightarrow \infty$ as $n\rightarrow \infty$.

In what follows we shall use the Lagrange multipliers rule to show that every positive level set of the functional F defined by (2.1) contains an eigenfunction of the problem (1.1) and we shall find its corresponding eigenvalue in terms of the pointed out eigenfunction. Such an eigenfunction will appear as a solution of the minimum problem

$$\begin{aligned} \min _{u\in \mathscr {C}\cap S_F(\alpha )}H(u), \end{aligned}$$

(2.16)

where H is defined by

$$\begin{aligned} H:W\rightarrow [0,\infty ), \ H(u):=\displaystyle \frac{1}{p}\int _{\varOmega _1} \mid \nabla u\mid ^{p} \hbox {d}x+\displaystyle \frac{1}{q}\int _{\varOmega _2} \mid \nabla u\mid ^{q} \hbox {d}x, \quad \forall ~u\in W, \end{aligned}$$

(2.17)

$\mathscr {C}$ is defined by (1.5) and $S_F(\alpha )$ is the set at the level $\alpha >0$ of F, i.e.

$$\begin{aligned} S_F(\alpha ):=\{u\in W;~F(u)=\alpha \},\quad \forall ~\alpha >0. \end{aligned}$$

In this respect we first recall the Lagrange multipliers principle (see, for example, [14, Thm. 2.2.18, p. 78]):

Lemma 2.2

Let X, Y be real Banach spaces and let $f:D\rightarrow \mathbb {R}$ be Fréchet differentiable, $g\in C^1(D,Y)$, where $D\subseteq X$ is a nonempty open set. If $v_0$ is a local minimizer of the constraint problem

$$\begin{aligned} {\min }~f( w), \quad g( w)=0, \end{aligned}$$

and $\mathscr {R}(g'(v_0))$ (the range of $g'(v_0)$) is closed, then there exist $\lambda ^*\in \mathbb {R}$ and $y^{*}\in Y^{*}$, at least one of which is non zero, such that

$$\begin{aligned} \lambda ^*f'(v_0)+y^{*}\circ g'(v_0)=0, \end{aligned}$$

where $Y^{*}$ stands for the dual of Y.

Note that $\lambda ^*\ne 0$ whenever $g'(v_0)$ is onto and can be therefore chosen to be 1 in this particular case.

The eigenvalue problem corresponding to the minimum problem (2.16), via the Lagrange multipliers, is:

$$\begin{aligned} H'(u_\alpha )=\lambda _\alpha F'(u_\alpha ),~\lambda _\alpha >0, u_\alpha \ne 0. \end{aligned}$$

(2.18)

Its variational version is (1.4).

Theorem 2.2

Let F and H be the functionals defined by (2.1) and (2.17). For every $2\le p<q,~ \alpha >0$, the minimization problem (2.16) has a solution $u_\alpha$ which is an eigenfunction of the eigenvalue problem (2.18) and therefore a solution of the variational version (1.4) of the initial eigenvalue problem (1.1).

Proof

Let us first show that the set $\mathscr {C}\cap S_F(\alpha )$ is nonempty for every $\alpha >0.$ Indeed, if we choose $w\in \mathscr {C}\cap C_0^\infty (\varOmega _1)$, nonzero, then $\alpha w/ F(w)\in \mathscr {C}\cap S_F(\alpha ).$

Now, the functional H is coercive on the weakly closed subset $\mathscr {C}\cap S_F(\alpha )$ of the reflexive Banach space W, i.e.,

$$\begin{aligned} \displaystyle \lim _{{\mathop {u\in \mathscr {C}\cap S_F(\alpha )}\limits ^{\parallel u\parallel _{W}\rightarrow \infty }}}H(u)=\infty . \end{aligned}$$

This fact is a simple consequence of the equality

$$\begin{aligned} \displaystyle \lim _{{\mathop {u\in S_F(\alpha )}\limits ^{\parallel u\parallel _{W}\rightarrow \infty }}}(\parallel \nabla u\parallel _{L^p(\varOmega _1)}+\parallel \nabla u\parallel _{L^q(\varOmega _2)})=\infty . \end{aligned}$$

On the other hand, the weakly lower semicontinuity of the norms in $L^p(\varOmega _1)$ and $L^q(\varOmega _2)$ implies the weakly lower semicontinuity of the functional H on $\mathscr {C}\cap S_F(\alpha ).$ Then, we can apply [16, Theorem 1.2] in order to obtain the existence of a global minimum point of H over $\mathscr {C}\cap S_F(\alpha )$, say $u_\alpha$, i.e., $H(u_\alpha )=\min _{u\in \mathscr {C}\cap S_F(\alpha )}H(u)$. Obviously, $u_\alpha \in \mathscr {C}\cap S_F(\alpha )$ implies that $u_\alpha$ is a nonconstant function. In fact, $u_\alpha$ is a solution of the minimization problem

$$\begin{aligned} \min _{ w\in W} {H}( w), \end{aligned}$$

under the restrictions

$$\begin{aligned} g( w):=&\displaystyle \frac{1}{p}\int _{\varOmega _1} \mid w\mid ^{p} \hbox {d}x+\displaystyle \frac{1}{q}\int _{\varOmega _2} \mid w\mid ^{q}\hbox {d}x-\alpha =0, \\ h( w):=&\int _{\varOmega _1} \mid w\mid ^{p-2} w ~\hbox {d}x+ \int _{\varOmega _2} \mid w\mid ^{q-2} w ~\hbox {d}x=0,\quad \forall ~ w\in W. \end{aligned}$$

We can apply Lemma 2.2 with $X=W,~ D=W{\setminus } \{0\},~Y=\mathbb {R}, f=H,$$g,~h:W\rightarrow \mathbb {R}$ being the functions just defined above, and $v_0=u_\alpha ,$ on the condition that $\mathscr {R}(g'(u_\alpha )), \mathscr {R}(h'(u_\alpha ))$ be closed sets. In fact, we can show that $g'(u_\alpha ),~h'(u_\alpha )$ are surjective, i.e. $\forall ~~ c_1, c_2\in \mathbb {R}$ there exist $w_1, w_2\in W$ such that

$$\begin{aligned} \langle g'(u_\alpha ),w_1\rangle =c_1, \langle h'(u_\alpha ),w_2\rangle =c_2. \end{aligned}$$

We seek $w_1, w_2$ of the form $w_1=~\beta u_\alpha ,~w_2=\gamma$, with $\beta ,\gamma \in \mathbb {\mathbb {R}}$. Thus, we obtain from the above equations

$$\begin{aligned} \beta \Big (\int _{\varOmega _1} \mid u_\alpha \mid ^{p} \hbox {d}x+\int _{\varOmega _2} \mid u_\alpha \mid ^{q} \hbox {d}x\Big )= & {} c_1, \\ \gamma \Big ((p-1)\int _{\varOmega _1} \mid u_\alpha \mid ^{p-2} \hbox {d}x+(q-1)\int _{\varOmega _2} \mid u_\alpha \mid ^{q-2} \hbox {d}x\Big )= & {} c_2 \end{aligned}$$

which have unique solutions $\beta , \gamma$ since $u_\alpha \in S_F(\alpha )$ implies that

$$\begin{aligned} r_1\int _{\varOmega _1} \mid u_\alpha \mid ^{p_1} ~\hbox {d}x+r_2\int _{\varOmega _2} \mid u_\alpha \mid ^{q_1} ~\hbox {d}x>0,\quad \forall ~p_1, q_1, r_i>0,~i=1,2. \end{aligned}$$

Thus, by Lemma 2.2, there exist $\lambda$ and $\mu \in \mathbb {R}$ such that, $\lambda ^2+\mu ^2>0$ and for all $w\in W,$

$$\begin{aligned}&\int _{\varOmega _1} \mid \nabla u_\alpha \mid ^{p-2}\nabla u_\alpha \cdot \nabla w~\hbox {d}x+\int _{\varOmega _2} \mid \nabla u_\alpha \mid ^{q-2}\nabla u_\alpha \cdot \nabla w~\hbox {d}x\nonumber \\&\quad -\,\lambda \Big (\int _{\varOmega _1} \mid u_\alpha \mid ^{p-2} u_\alpha w~\hbox {d}x+\int _{\varOmega _2} \mid u_\alpha \mid ^{q-2} u_\alpha w~\hbox {d}x\Big )\nonumber \\&\quad -\,\mu \Big ((p-1)\int _{\varOmega _1}\mid u_\alpha \mid ^{p-2} w~\hbox {d}x+(q-1)\int _{\varOmega _2} \mid u_\alpha \mid ^{q-2} w~\hbox {d}x\Big ) =0. \end{aligned}$$

(2.19)

Testing with $w=1$ in (2.19) and observing that $u_\alpha$ belongs to $\mathscr {C}$, we deduce that $\mu =0$ and therefore $\lambda \ne 0$. By choosing $w=u_\alpha$ in (2.19), we find $K_{1\alpha }-\lambda K_{2\alpha }=0$, where $K_{1\alpha }$ and $K_{2\alpha }$ denote the constants

$$\begin{aligned} \int _{\varOmega _1} \mid \nabla u_\alpha \mid ^{p}~\hbox {d}x+\int _{\varOmega _2} \mid \nabla u_\alpha \mid ^{q}\hbox {d}x \text{ and } \int _{\varOmega _1} \mid u_\alpha \mid ^{p}~\hbox {d}x+\int _{\varOmega _2} \mid u_\alpha \mid ^{q}\hbox {d}x, \end{aligned}$$

respectively, which are positive as $u_\alpha \in \mathscr {C}\cap S_F(\alpha )$. In other words (2.19) becomes

$$\begin{aligned}&\int _{\varOmega _1} \mid \nabla u_\alpha \mid ^{p-2}\nabla u_\alpha \cdot \nabla w~\hbox {d}x+\int _{\varOmega _2} \mid \nabla u_\alpha \mid ^{q-2}\nabla u_\alpha \cdot \nabla w~\hbox {d}x\nonumber \\&\quad = \lambda _{\alpha }\Big (\int _{\varOmega _1} \mid u_\alpha \mid ^{p-2} u_\alpha w~\hbox {d}x +\int _{\varOmega _2} \mid u_\alpha \mid ^{q-2} u_\alpha w~\hbox {d}x\Big ), \end{aligned}$$

(2.20)

where

$$\begin{aligned} \lambda _{\alpha }=\displaystyle \frac{K_{1\alpha }}{K_{2\alpha }}= \displaystyle \frac{\int _{\varOmega _1} \mid \nabla u_\alpha \mid ^{p}~\hbox {d}x+ \int _{\varOmega _2} \mid \nabla u_\alpha \mid ^{q}~\hbox {d}x}{\int _{\varOmega _1} \mid u_\alpha \mid ^{p}~\hbox {d}x+\int _{\varOmega _2} \mid u_\alpha \mid ^{q}~\hbox {d}x}. \end{aligned}$$

Thus, $(\lambda _{\alpha }, u_\alpha )$ is an eigenpair of problem (1.4). $\square$

Remark 2.2

The results we have proved so far are also valid for the eigenvalue problem obtained out of (1.1) by replacing Eq. (1.1)$_2$ with the equation

$$\begin{aligned} -\varDelta _q u_2=\lambda \mid u_2\mid ^{p-2}u_2\quad \text{ in } ~ \varOmega _2, \end{aligned}$$

(2.21)

for $1<p<q.$ In this case we shall consider the same space W but endowed with the norm

$$\begin{aligned} \mid \parallel u\mid \parallel :=\parallel u\parallel _{W^{1,p}(\varOmega _1)}+\parallel \nabla u\parallel _{L^q(\varOmega _2)}+\parallel u\parallel _{L^p(\varOmega _2)},\quad \forall ~u\in W. \end{aligned}$$

(2.22)

If $p\le q$, then $\mid \parallel \cdot \mid \parallel$ is a norm in W equivalent with the usual norm $\parallel \cdot \parallel _W$ of this space. This fact follows from [4, Proposition 3.9.55].

In this case, the variational version of the new eigenvalue problem is:

Find $\lambda \in \mathbb {R}$ for which there exists $u\in W {\setminus } \{0\}$ such that

$$\begin{aligned}&\int _{\varOmega _1} \mid \nabla u\mid ^{p-2}\nabla u \cdot \nabla w~\hbox {d}x+\int _{\varOmega _2}\mid \nabla u\mid ^{q-2}\nabla u \cdot \nabla w~\hbox {d}x \nonumber \\&\quad =\lambda \int _{\varOmega } \mid u\mid ^{p-2} u w~\hbox {d}x,\quad \forall ~ w\in W. \end{aligned}$$

(2.23)

In order to obtain the counterpart of Theorem 2.1 for this new eigenvalue transmission problem, we need to verify the conditions $(h_1)-(h_3)$ of Lemma 2.1. We shall define for this new context the corresponding functionals $F_p, G_p:W\rightarrow [0,\infty )$

$$\begin{aligned} F_p(u):=\displaystyle \frac{1}{p}\int _{\varOmega } \mid u\mid ^{p} \hbox {d}x,~G_p(u):=F_p(u)+\displaystyle \frac{1}{p}\int _{\varOmega _1} \mid \nabla u\mid ^{p}\hbox {d}x+\displaystyle \frac{1}{q}\int _{\varOmega _2} \mid \nabla u\mid ^{q} \hbox {d}x. \end{aligned}$$

(2.24)

All calculations are similar to those we did to prove $(h_1)-(h_3)$ in the case of the eigenvalue transmission problem (1.1), except the one which verifies the property $(S_0)$ on $G_p^{\prime }$ of $(h_2).$ In order to prove $(S_0)$, we define the functional $J:W\rightarrow W^*$

$$\begin{aligned} \langle J(u), w\rangle :=\int _{\varOmega _2} \mid u\mid ^{p-2}u w ~\hbox {d}x-\int _{\varOmega _2} \mid u\mid ^{q-2}u w ~\hbox {d}x,\quad \forall ~u, w\in W. \end{aligned}$$

One can show, by using the same type of arguments as we did to prove $(h_1)$ and Lemma 2.1, that J(u) is strongly continuous. Let us consider

$$\begin{aligned} u_n\rightharpoonup u,~G_p'(u_n)\rightharpoonup w_p, ~\langle G_p'(u_n), u_n\rangle \rightarrow \langle w_p, u\rangle ~\text{ as }~n\rightarrow \infty \end{aligned}$$

for some $u\in W,~ w_p\in W^*$ and we shall show that $u_n\rightarrow u.$ In this respect (see also the argument within the proof of the statement $(h_2)$) it is sufficient to show that $\parallel u_n\parallel _W\rightarrow \parallel u\parallel _W$, as $\parallel \cdot \parallel _W$ and $\mid \parallel \cdot \mid \parallel$ are equivalent norms on W. In this regard we observe that

$$\begin{aligned} G'(u_n)=G_p'(u_n)-J(u_n)\rightharpoonup w_p-J(u), \langle G'(u_n), u_n\rangle \rightarrow \langle w_p-J(u), u\rangle , \end{aligned}$$

which combined with the $(S_0)$ property of $G'$ implies the desired statement.

The counterpart of Theorem  2.2 can be obtained with no difficulty, by using arguments similar to those we have used in the case of the eigenvalue transmission problem (1.1).

3 Extensions

In this section we discuss some extensions of the previous results.

4 An eigenvalue–transmission problem with Robin boundary conditions

Following the same type of arguments, one can actually prove the counterparts of Theorem 2.1 and Theorem 2.2 for the following more general eigenvalue–transmission problem, involving Robin conditions on $\varGamma _1$ and $\varGamma _2$, namely

$$\begin{aligned} \left\{ \begin{array}{l} -\varDelta _p u_1=\lambda \mid u_1\mid ^{p-2}u_1\quad \text{ in } ~ \varOmega _1,\\ -\varDelta _q u_2=\lambda \mid u_2\mid ^{q-2}u_2\quad \text{ in } ~ \varOmega _2,\\ \displaystyle \frac{\partial u_1}{\partial \nu _{p}}+\beta _1|u_1|^{p-2}=0 ~~ \text{ on } ~ \varGamma _1,\\ \displaystyle \frac{\partial u_2}{\partial \nu _{q}}+\beta _2|u_2|^{q-2}=0 ~~ \text{ on } ~ \varGamma _2,\\ u_1=u_2,~~\displaystyle \frac{\partial u_1}{\partial \nu _{p}} =\displaystyle \frac{\partial u_2}{\partial \nu _{q}}~~ \text{ on } ~ \varGamma , \end{array}\right. \end{aligned}$$

(3.1)

where $\beta _1,\beta _2\ge 0$. The variational version of problem (3.1) is:

Proposition 3.1

The scalar $\lambda \in \mathbb {R}$ is an eigenvalue of the problem (3.1) if and only if there exists $u\in W {\setminus } \{0\}$ such that

$$\begin{aligned}&\int _{\varOmega _1} \mid \nabla u\mid ^{p-2}\nabla u \cdot \nabla w~\hbox {d}x+\int _{\varOmega _2}\mid \nabla u\mid ^{q-2}\nabla u \cdot \nabla w~\hbox {d}x\nonumber \\&\qquad + \beta _1\int _{\partial \varOmega _1} \mid u\mid ^{p-2} u w~\hbox {d}\sigma +\beta _2\int _{\partial \varOmega _2} \mid u\mid ^{q-2} u w~\hbox {d}\sigma \nonumber \\&\quad = \lambda \Big (\int _{\varOmega _1} \mid u\mid ^{p-2} u w~\hbox {d}x+\int _{\varOmega _2} \mid u\mid ^{q-2} u w~\hbox {d}x\Big ), \quad \forall w\in W. \end{aligned}$$

(3.2)

While the functional playing the role of F in this setting remains unchanged, the functional playing the role of $G:W\longrightarrow \mathbb {R}$ is given by

$$\begin{aligned} G(u) :=&\displaystyle \frac{1}{p}\int _{\varOmega _1}\big ( \mid \nabla u\mid ^{p} +\mid u\mid ^{p}\big ) ~\hbox {d}x+\displaystyle \frac{1}{q}\int _{\varOmega _2} \big ( \mid \nabla u\mid ^{q}+ \mid u\mid ^{q}\big ) ~\hbox {d}x\nonumber \\&+\displaystyle \frac{1}{p}\int _{\partial \varOmega _1}\beta _1 \mid u\mid ^{p}\hbox {d}\sigma +\displaystyle \frac{1}{q}\int _{\partial \varOmega _2}\beta _2\mid u \mid ^q\hbox {d}\sigma . \end{aligned}$$

(3.3)

5 The counterpart of problem (1.1) in the Riemannian setting

Let (M, g) be a compact boundaryless Riemannian manifold and $\varOmega \subseteq M$ be a connected open set such that $\varOmega _-:=M{\setminus }\overline{\varOmega }$ is also connected. We denote $\varOmega$ by $\varOmega _+$ and the common boundary of $\varOmega _+$ and $\varOmega _-$ by $\partial \varOmega$, which is assumed to be a hypersurface of M. We consider the following coupled problem

$$\begin{aligned} \left\{ \begin{array}{l} -\varDelta _p u_+=\lambda \mid u_+\mid ^{p-2}u_+\quad \text{ in } ~ \varOmega _+,\\ -\varDelta _q u_-=\lambda \mid u_-\mid ^{q-2}u_-\quad \text{ in } ~ \varOmega _-,\\ u_+=u_-,~~ \displaystyle \frac{\partial u_+}{\partial \nu _{p}}=\displaystyle \frac{\partial u_-}{\partial \nu _{q}}~~ \text{ on } ~ \partial \varOmega , \end{array}\right. \end{aligned}$$

(3.4)

where $\varDelta _r w$ stands for the r-Laplace operator $\text{ div }\big ( \mid \nabla w\mid ^{r-2} \nabla w\big )$.

Proposition 3.2

The scalar $\lambda \in \mathbb {R}$ is an eigenvalue of the problem (3.4) if and only if there exists $u\in W_\varOmega {\setminus } \{0\}$ such that

$$\begin{aligned}&\int _{\varOmega _+} \mid \nabla u\mid ^{p-2}\nabla u \cdot \nabla w~\hbox {d}x+\int _{\varOmega _-}\mid \nabla u\mid ^{q-2}\nabla u \cdot \nabla w~\hbox {d}x \nonumber \\&\quad =\lambda \Big (\int _{\varOmega _+} \mid u\mid ^{p-2} u w~\hbox {d}x+\int _{\varOmega _-} \mid u\mid ^{q-2} u w~\hbox {d}x\Big ),\quad \forall ~ w\in W_\varOmega , \end{aligned}$$

(3.5)

where

$$\begin{aligned} W_\varOmega :=\big \{u\in W^{1,p}(M) :~ u\vert _{\varOmega _-}\in W^{1,q}(\varOmega _-) \big \}. \end{aligned}$$

(3.6)

The proof of Proposition 3.2 works along the same lines with the proof of Proposition 1.1 and partly relies on the integration by parts formula [12, p. 383]

$$\begin{aligned} \displaystyle \int _X(f\mathrm{div}X) dV_g=-\displaystyle \int _Xg(X,\mathrm{grad}f)\hbox {d}V_g+\displaystyle \int _{\partial X}g(X,\nu )\hbox {d}V_{\tilde{g}} \end{aligned}$$

where (X, g) is a compact oriented Riemannian manifold, $\nu$ is the outward unit normal vector field on $\partial X$, and $\tilde{g}$ is the Riemannian metric on $\partial X$ induced by g.

We endow $W_\varOmega$ with the norm

$$\begin{aligned} \parallel u\parallel _{W_\varOmega }:=\parallel u\vert _{\varOmega _+}\parallel _{W^{1,p}(\varOmega _+)}+\parallel u\vert _{\varOmega _-}\parallel _{W^{1,q}(\varOmega _-)},\quad \forall ~u\in W_\varOmega \end{aligned}$$

where $\parallel \cdot \parallel _{W^{1,p}(\varOmega _+)}$ and $\parallel \cdot \parallel _{W^{1,q}(\varOmega _-)}$ are the usual norms of the Sobolev spaces $W^{1,p}(\varOmega _+)$ and $W^{1,q}(\varOmega _-)$, respectively.

Remark 3.1

The space $W_\varOmega$ defined before can be identified with the space

$$\begin{aligned} \widetilde{W}_\varOmega :=\{(u_+,u_-)\in W^{1,p}(\varOmega _+)\times W^{1,q}(\varOmega _-); ~\text{ Tr }^{\varOmega _+}~u_+=~\text{ Tr }^{\varOmega _-} ~u_-~~\text{ on }~\partial \varOmega \}. \end{aligned}$$

Note that $W_\varOmega$ is a reflexive Banach space, as it is a closed subspace of the reflexive product $W^{1,p}(\varOmega _+)\times W^{1,q}(\varOmega _-)$ with reflexive factors (see [1, p. 70], [6, p. 11] or [7, p. 20]). Define the functionals F and G on $W_\varOmega$:

$$\begin{aligned}&\displaystyle F(u):= \frac{1}{p}\int _{\varOmega _+} \mid u\mid ^{p}\hbox {d}x+\displaystyle \frac{1}{q}\int _{\varOmega _-} \mid u\mid ^{q}\hbox {d}x, \end{aligned}$$

(3.7)

$$\begin{aligned}&\displaystyle G(u):= \frac{1}{p}\int _{\varOmega _+}\big ( \mid \nabla u\mid ^{p} +\mid u\mid ^{p}\big ) ~\hbox {d}x+\displaystyle \frac{1}{q}\int _{\varOmega _-} \big ( \mid \nabla u\mid ^{q}+ \mid u\mid ^{q}\big ) ~\hbox {d}x, \end{aligned}$$

(3.8)

for all $u\in W_\varOmega .$ It is easily seen that functionals F and G are of class $C^1$ on $W_\varOmega$ and obviously F, G are even with $F(0)=G(0)=0$. We also have

$$\begin{aligned}&\displaystyle \langle F'(u), w\rangle = \int _{\varOmega _+} \mid u\mid ^{p-2}u w ~\hbox {d}x+\int _{\varOmega _-} \mid u\mid ^{q-2}u w ~\hbox {d}x, \\&\displaystyle \langle G'(u), w\rangle = \langle F'(u), w\rangle + \int _{\varOmega _+} \mid \nabla u\mid ^{p-2}\nabla u \cdot \nabla w ~\hbox {d}x+\int _{\varOmega _-} \mid \nabla u\mid ^{q-2} \nabla u \cdot \nabla w ~\hbox {d}x, \end{aligned}$$

for all $w\in W_\varOmega .$ We denote by $S_G(1)$ the level set $\{u\in W_\varOmega ;~G(u)=1\}$ of G.

The following auxiliary result can be proved in a similar way with Lemma 2.1.

Lemma 3.1

The functionals F and G satisfy the following properties:

$(\mathfrak {h}_1)$ :

$F'$ is strongly continuous, i.e. $u_n\rightharpoonup u$ in $W_\varOmega \Rightarrow F'(u_n) \rightarrow F'(u)$ and

$$\begin{aligned} \langle F'(u),u\rangle =0\Rightarrow u=0; \end{aligned}$$

$(\mathfrak {h}_2)$ :

$G'$ is bounded and satisfies condition $(S_0),$ i.e.,

$$\begin{aligned} u_n\rightharpoonup u,~G'(u_n)\rightharpoonup w, ~\langle G'(u_n), u_n\rangle \rightarrow \langle w, u\rangle ~\Rightarrow ~u_n\rightarrow u; \end{aligned}$$

$(\mathfrak {h}_3)$ :

$S_G(1)$ is bounded and if $u\ne 0$ then

$$\begin{aligned} \langle G'(u), u\rangle>0,~~\lim _{t\rightarrow \infty }G(tu)=\infty ,~\inf _{u\in S_G(1)}\langle G'(u), u\rangle >0. \end{aligned}$$

According to the properties $(\mathfrak {h}_1)-(\mathfrak {h}_3)$, verified by the functionals F and G, combined with their properties to be even and to vanish at zero, it follows, via the Lusternik–Schnirelmann principle, that the eigenvalue problem

$$\begin{aligned} F'(u)=\mu G'(u),~u\in S_G(1) \end{aligned}$$

(3.9)

admits a sequence of eigenpairs $\{(u_n ,\mu _n )\}$ such that $u_n \rightharpoonup 0$, $\mu _n\longrightarrow 0$ as $n\longrightarrow \infty$ and $\mu _n\ne 0$, for all n.

Theorem 3.1

The sequence $\{\mu _n\}$ of eigenvalues of the problem (3.9) produces a nondecreasing sequence $\lambda _n=\displaystyle \frac{1}{\mu _n}-1$ of eigenvalues of the problem (3.4) and obviously $\lambda _n\rightarrow \infty$ as $n\rightarrow \infty$.

Consider the minimization problem

$$\begin{aligned} \min _{u\in \mathscr {C}_\varOmega \cap S_F(\alpha )}H(u), \end{aligned}$$

(3.10)

where

$$\begin{aligned} H:W_\varOmega \rightarrow [0,\infty ), \ H(u):=&\displaystyle \frac{1}{p}\int _{\varOmega _+} \mid \nabla u\mid ^{p} \hbox {d}x+\displaystyle \frac{1}{q}\int _{\varOmega _-} \mid \nabla u\mid ^{q} \hbox {d}x, \quad \forall ~u\in W_\varOmega , \end{aligned}$$

(3.11)

$$\begin{aligned} \mathscr {C}_\varOmega :=&\Big \{ u\in W_\varOmega ;~\int _{\varOmega _+} \mid u\mid ^{p-2} u ~\hbox {d}x+ \int _{\varOmega _-} \mid u\mid ^{q-2} u ~\hbox {d}x=0\Big \}. \end{aligned}$$

(3.12)

and $S_F(\alpha )$ is the set at the level $\alpha >0$ of F (i.e. $S_F(\alpha ):=\{u\in W;~F(u)=\alpha \}$).

The eigenvalue problem corresponding to the minimization problem (3.10), via the Lagrange multipliers, is:

$$\begin{aligned} H'(u_\alpha )=\lambda _\alpha F'(u_\alpha ),~\lambda _\alpha >0, u_\alpha \ne 0, \end{aligned}$$

(3.13)

Its variational version is (3.5).

Theorem 3.2

Let F and H be the functionals defined by (3.7) and (3.11). For every $2\le p<q,~ \alpha >0$, the problem (3.10) has a solution $u_\alpha$ which is an eigenfunction of the eigenvalue problem (3.13) and therefore a solution of the variational version (3.5) of the eigenvalue problem (3.4).

Remark 3.2

Note that in (3.4) there is no boundary condition, because the ambient manifold M is boundary-free. One can think of the eigenvalue–transmission counterpart of the problem (1.1) in a more general Riemannian setting, where the ambient manifold M has nonempty boundary and the interface hypersurface is suitably chosen. Indeed, for a compact Riemannian manifold (M, g) with nonempty boundary, we consider a connected open set $\varOmega _1\subseteq M$ such that $\varOmega _2:=M{\setminus }\overline{\varOmega }_1$ is also connected and $\overline{\varOmega }_1$, $\overline{\varOmega }_2$ are manifolds with boundaries $\partial \varOmega _1$, $\partial \varOmega _2$. We further assume that their common boundary part $\varGamma :=\partial \varOmega _1\cap \partial \varOmega _2$ is a hypersurface of M (which is closed), such that $\varGamma _1:=\partial \varOmega _1{\setminus }\varGamma$ and $\varGamma _2:=\partial \varOmega _2{\setminus } \varGamma$ are also connected. With such choices the eigenvalue–transmission counterpart of the problem (1.1) in this more general Riemannian setting looks like (1.1).