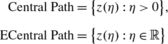Abstract
We develop a natural generalization to the notion of the central path, a concept that lies at the heart of interior-point methods for convex optimization. The generalization is accomplished via the “derivative cones” of a “hyperbolicity cone”, the derivatives being direct and mathematically appealing relaxations of the underlying (hyperbolic) conic constraint, be it the non-negative orthant, the cone of positive semidefinite matrices, or other.
We prove that a dynamics inherent to the derivative cones generates paths always leading to optimality, the central path arising from a special case in which the derivative cones are quadratic. Derivative cones of higher degree better fit the underlying conic constraint, raising the prospect that the paths they generate lead to optimality quicker than the central path.
Similar content being viewed by others
Notes
Central Path :={x(η):η>0} where x(η) solves min x ηc ∗ x−lnp(x), s.t. Ax=b, x∈Λ ++.
The “relative interior” of a convex set \(S \subseteq \mathcal{E} \) is the interior of S when considered as a subset in the smallest affine space containing S (where the affine space inherits the topology of the Euclidean space \(\mathcal{E}\)).
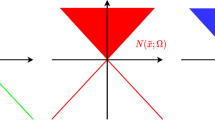
To gain a sense of the difficulties (and how first impressions can mislead), consider that for any value 0<T≤∞, it is straightforward to define dynamics on \(\mathbb{R}^{2} \) that generates a pair of paths a(t), b(t) for which \(\dot{b}(t) = a(t) - b(t) \) and as t→T, a(t) spirals outward to infinity whereas b(t) spirals inward to a point. (Thus, although a(t) is “leading” b(t), the paths end (infinitely) far apart.)
The dual cone \(\varLambda_{+}^{*} \) consists of the linear functionals s ∗ satisfying s ∗ x≥0 for all x∈Λ +.
This is proven simply by observing that for feasible x and (y ∗,s ∗),
$$c^*x = \bigl(y^*A + s^*\bigr)x = y^*b + s^*x \geq y^*b , $$the inequality being due to x∈Λ + and \(s^{*} \in \varLambda_{+}^{*} \).
More specifically, after understanding the paper the reader likely will not have much difficulty in showing the following, in which
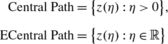
(“extended central path”), and z(η) solves min x ηc ∗ x−lnp(x), s.t., Ax=b, x∈Λ ++:
-
\(\mathrm {Central \ Path}\subseteq \mathrm {Swath}(n-2) \).
-
If \(e(0) \in \mathrm {ECentral \ Path}\cap (\mathrm {Swath}(n-2) \setminus \mathrm {Core}(n-2)) \), then T(e(0))=∞ and
$$\bigl\{ e(t): 0 \leq t < \infty \bigr\} = \bigl\{ e \in \mathrm {ECentral \ Path}: c^* e \leq c^* e(0) \bigr\} . $$ -
If \(e \in \mathrm {ECentral \ Path}\cap \mathrm {Core}(n-2) \) then
$$\mathrm {Core}(n-2) = \ell \cap \varLambda_{++} = \mathrm {ECentral \ Path}, $$where ℓ is the line containing e and the (unique) point in \(\mathrm {Opt}_{{e}}^{({n-2})} = \mathrm {Opt} \).
-
To see that Core(n−1)=∅, recall that \((\partial \varLambda ^{({n-1})}_{+,{e}}) \cap \varLambda_{+} \) is precisely the lineality space of Λ + (by Theorem 4.1(C)). Thus, since Λ + is regular (by assumption) and since the origin is infeasible (because b≠0), the boundary of Feas cannot intersect the boundary of \(\mathrm {Feas}^{({n-1})}_{{e}} \); in particular, it cannot happen that Opt intersects \(\mathrm {Opt}_{{e}}^{({n-1})} \).
References
H.H. Bauschke, O. Güler, A.S. Lewis, H.S. Sendov, Hyperbolic polynomials and convex analysis, Can. J. Math. 53(3), 470–488 (2001).
J. Borcea, P. Brändén, Multivariate Pólya–Schur classification problems in the Weyl algebra, Proc. Lond. Math. Soc. 101(1), 73–104 (2010).
P. Brändén, Obstructions to determinantal representability, Adv. Math. 226(2), 1202–1212 (2011).
C.B. Chua, The primal-dual second-order cone approximations algorithm for symmetric cone programming, Found. Comput. Math. 7(3), 271–302 (2007).
A.V. Fiacco, G.P. McCormick, Nonlinear Programming: Sequential Unconstrained Minimization Techniques (SIAM, Philadelphia, 1990).
L. Gårding, An inequality for hyperbolic polynomials, J. Math. Mech. 8(6), 957–965 (1959).
O. Güler, Hyperbolic polynomials and interior point methods for convex programming, Math. Oper. Res. 22(2), 350–377 (1997).
L. Gurvits, Van der Waerden/Schrijver-Valiant like conjectures and stable (aka hyperbolic) homogeneous polynomials: one theorem for all, Electron. J. Comb. 15(#R66) (2008).
F.R. Harvey, H.B. Lawson Jr., Hyperbolic polynomials and the Dirichlet problem. arXiv:0912.5220v2 [math.AP].
J. Helton, V. Vinnikov, Linear matrix inequality representations of sets, Commun. Pure Appl. Math. 60(5), 654–674 (2007).
A.S. Lewis, P.A. Parrilo, M.V. Ramana, The Lax conjecture is true, Proc. Am. Math. Soc. 133(9), 2495–2499 (2005).
Y. Nesterov, A. Nemirovski, Interior-Point Polynomial Algorithms in Convex Programming (SIAM, Philadelphia, 1994).
J. Renegar, Hyperbolic programs, and their derivative relaxations, Found. Comput. Math. 6(1), 59–79 (2006).
Y. Zinchenko, The local behavior of the Shrink–Wrapping algorithm for linear programming, Ph.D. thesis, Cornell University (2005).
Y. Zinchenko, Shrink-wrapping trajectories for linear programming. arXiv:1005.5522v1 [math.OC].
Acknowledgements
Thanks to Chek Beng Chua and Yuriy Zinchenko for many helpful conversations. Deep gratitude also goes to the referees, whose extensive comments led to the paper being significantly restructured, and led to the (motivational) exposition being considerably expanded especially in the proofs.
Research supported in part by NSF Grant #CCF-0430672.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Michael Todd.
Rights and permissions
About this article
Cite this article
Renegar, J. Central Swaths. Found Comput Math 13, 405–454 (2013). https://doi.org/10.1007/s10208-013-9148-x
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10208-013-9148-x
Keywords
- Hyperbolicity cone
- Hyperbolic polynomial
- Hyperbolic programming
- Central path
- Conic programming
- Convex optimization