Abstract
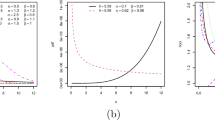
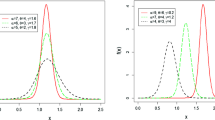
The exact distributions of many functions of random vectors are derived in the literature mainly for the case of a Gaussian vector distribution or under the assumption that the vector follows a spherical or an elliptically contoured distribution. Numerous standard statistical applications are given for these cases. Deriving analogous results, if the sample distribution comes from a large family of probability laws, needs to make use of new analytical tools from the area of exact distribution theory. The present paper provides the application of such tools suitable for deriving the exact cumulative distribution functions and density functions of extreme values, products, and ratios in \(l_{2,p}\)-symmetrically distributed populations. Accompanying simulation studies are presented in cases of power-exponentially distributed populations and for different sample sizes. As an application, well-known results on the increasing failure rate properties of extremes from Gaussian samples are extended to \(p\)-power exponential sample distributions.























Similar content being viewed by others
References
Adler, R., Eldman, R., Taqqu, M.: A Practical Guide to Heavy Tails: Statistical Techniques and Applications. Birkhäuser Bosten Inc, Cambridge (1998)
Anderson, T.: An Introduction to Multivariate Statistical Analysis, 2nd edn. Wiley, New York (1984)
Arellano-Valle, R., Genton, M.: On the exact distribution of the maximum of absolutely continuous dependent random variables. Stat. Probab. Lett. 78, 27–35 (2008)
Arellano-Valle, R., Richter, W.-D.: On skewed continuous \(l_{n, p}\)-symmetric distributions. Chil. J. Stat. 3(2), 193–212 (2012)
Arnold, B., Brockett, P.: On distributions whose component ratios are cauchy. Am. Stat. 46(1), 25–26 (1992)
Balkema, A., Embrechts, P.: High Risk Scenarios and Extremes: A Geometric Approach. Seminar for Applied Mathematics. European Mathematical Society Publishing House, Zürich (2007)
Batún-Cutz, J., González-Farías, G., Richter, W.-D.: Maximum distributions for \(l_{2, p}\)-symmetric vectors are skewed \(l_{1, p}\)-symmetric distributions. Stat. Probab. Lett. 83(10), 2260–2268 (2013). doi: 10.1016/j.spl.2013.06.022
David, H.: Order Statistics. Wiley, New York (1981)
Fang, K., Anderson, T.: Statistical Inference in Elliptically Contoured and Related Distributions. Allerton Press Inc, New York (1990)
Fang, K., Zhang, Y.: Generalized Multivariate Analysis. Springer, New York (1990)
Glaser, R.: Bath tub and related failure rate characterizations. J. Am. Stat. Assoc. 75, 667–672 (1980)
Gumbel, E.: Statistics of Extremes. Columbia University Press, New York (1958)
Günzel, T., Richter, W.-D., Scheutzow, S., Schicker, K., Venz, J.: Geometric approach to the skewed normal distribution. J. Stat. Plann. Inference 142(12), 3209–3224 (2012). doi:10.1016/j.jspi.2012.06.009
Gupta, A., Song, D.: \(l_p\)-norm spherical distributions. J. Stat. Plann. Inference 60(2), 241–260 (1997). doi: 10.1016/S0378-3758(96)00129-2
Gupta, A., Varga, T.: Elliptically Contoured Models in Statistics. Kluwer Academic Publishers Norwell, Dordrecht (1993)
Gupta, P., Gupta, R.: Failure rate of minimum and maximum of a multivariate normal distribution. Metrika 53, 39–49 (2001)
Harter, H.: On the distribution of wald’s classification statistic. Ann. Math. Stat. 22, 58–67 (1951)
Hyvärinen, A.: Some extensions of score matching. Comput. Stat. Data Anal. 51, 2499–2512 (2007). doi:10.1016/j.csda.2006.09.003
Jamalizadeh, A., Balakrishnan, N.: Distributions of order statistics and linear combinations of order statistics from an elliptical distribution as mixtures of unified skew-elliptical distributions. J. Multivar. Anal. 101(6), 1412–1427 (2010). doi:10.1016/j.jmva.2009.12.012
Kalke, S.: Geometrische Strukturen \(l_{n, p}\)-symmetrischer charakteristischer Funktionen. Dissertation, Universität Rostock (2013)
Kalke, S., Richter, W.-D.: Simulation of the p-generalized gaussian distribution. J. Stat. Comput. Simul. 83(4), 639–665 (2013). doi:10.1080/00949655.2011.631187
Kalke, S., Richter, W.-D., Thauer, F.: Linear combinations, products and ratios of simplicial or spherical variates. Commun. Stat. Theory Methods 42(3), 505–527 (2013). doi:10.1080/03610926.2011.579702
Moszyńska, M., Richter, W.-D.: Reverse triangle inequality. antinorms and semi-antinorms. Stud. Sci. Math. Hung. 49(1), 120–138 (2012). doi:10.1556/SScMath.49.2012.1.1192
Nadarajah, S.: On the product and ratio of laplace and bessel random variables. J. Appl. Math. 4, 393–402 (2005a)
Nadarajah, S.: Sums, products, and ratios of non-central beta variables. Commun. Stat. Theory Methods 34, 89–100 (2005b)
Nadarajah, S., Gupta, A.: On the product and ratio for the elliptically symmetric pearson type vii distribution. Random Oper. Stoch. Equ. 13(2), 139–146 (2005)
Nadarajah, S., Kotz, S.: Linear combinations, products and ratios of t random variables. Allg. Stat. Arch. 89(3), 263–280 (2005)
Nekoukhou, V., Alamatsaz, M.: A family of skew-symmetric laplace distributions. Stat. Papers 53, 685–696 (2012). doi:10.1007/s00362-011-0372-7
Press, S.: The t-ratio distribution. J. Am. Stat. Assoc. 64, 242–252 (1969)
Rachev, S., Rüschendorf, L.: Approximate independence of distributions on spheres and their stability properties. Ann. Probab. 19(3), 1311–1337 (1991). doi:10.1214/aop/1176990346
Richter, W.-D.: Generalized spherical and simplicial coordinates. J. Math. Anal. Appl. 336, 1187–1202 (2007). doi:10.1016/j.jmaa.2007.03.047
Richter, W.-D.: On \(l_{2, p}\)-circle numbers. Lith. Math. J. 48(2), 228–234 (2008a). doi: 10.1007/s10986-008-9002-z
Richter, W.-D.: On the pi-function for nonconvex \(l_{2, p}\)-circle discs. Lith. Math. J. 48(3), 332–338 (2008b). doi: 10.1007/s10986-008-9016-6
Richter, W.-D.: Continuous \(l_{n, p}\)-symmetric distributions. Lith. Math. J. 49(1), 93–108 (2009). doi: 10.1007/s10986-009-9030-3
Richter, W.-D.: Exact distributions under non-standard model assumptions. AIP Conf. Proc. 1479, 442–445 (2012). doi:10.1063/1.4756160
Richter, W.-D.: Geometric and stochastic representations for elliptically contoured distributions. Commun. Stat. Theory Methods 42, 579–602 (2013). doi:10.1080/03610926.2011.611320
Richter, W.-D.: Geometric disintegration and star-shaped distributions. Submitted (2014a)
Richter, W.-D.: Norm contoured distributions in \(\mathbb{R}^2\). Submitted (2014b)
Schechtman, G., Zinn, J.: On the volume of the intersection of two \(l_p^n\) balls. Proc. Am. Math. Soc. 110(1), 217–224 (1990)
Sinz, F., Bethge, M.: The conjoint effect of divisive normalization and orientation selectivity on redundancy reduction in natural images. In: Proceedings of Front Computing Neuroscience Conference Abstract: Bernstein Symposium 2008, (2008)oi:10.3389/conf.neuro.10.2008.01.116
Song, D., Gupta, A.: \(l_p\)-norm uniform distributions. Proc. Am. Math. Soc. 125(2), 595–601 (1997)
Steutel, F., van Harn, K.: Infinite Divisibility of Probability Distributions on the Real Line. Marcel Dekker, New York (2004)
Subbotin, M.: On the law of frequency errors. Mat. Sb. 31, 296–301 (1923)
Szablowski, P.: Uniform distributions on spheres in finite dimensional \(l_\alpha \) and their generations. J. Multivar. Anal. 64(2), 103–117 (1998). doi: 10.1006/jmva.1997.1718
Tang, Q.: From light tail to heavy tails through multiplier. Extremes 11(4), 379–391 (2008). doi:10.1007/s10687-008-0063-5
Vázquez, A., Oliviera, J., Dezsö, Z., Goh, K.I., Kondor, I., Barabábsi, A.L.: Modeling bursts and heavy tails in human dynamics. Phys. Rev. E73, 036127 (2006). doi:10.1103/PhysRevE.73.036127
Acknowledgments
The authors are grateful to the Associated Editor and a reviewer for giving valuable hints which led to improvements in the presentation of the material.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Müller, K., Richter, WD. Exact extreme value, product, and ratio distributions under non-standard assumptions. AStA Adv Stat Anal 99, 1–30 (2015). https://doi.org/10.1007/s10182-014-0228-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10182-014-0228-2