1 Introduction

There is a multitude of applications in which it can be believed that one or more predictors have a monotonic relationship with the response variable, i.e., the response function is non-decreasing (or non-increasing) when one or more of these predictors increase. Such applications can be found in psychology, biology, signal processing, economics and many other disciplines [1, 2, 21, 22]. Perhaps the most widely known approach which allows for extracting a monotonic dependence is monotonic regression (MR) [5, 38].

In this paper, we consider the case of a model with one predictor \(x \in R\). The corresponding MR problem can be formulated as follows. Let f(x) be an unknown monotonic true response function. Given n observations \((X_1,Y_1), \ldots ,(X_n,Y_n)\), where \(X_i\in R\) and \(Y_i\in R\) are the observed predictor and response values, respectively. The values of \(Y_i\) are random with mean \(f(X_i)\). The predictor values are sorted as \(X_1<X_2< \ldots <X_n\). It is required that the fitted response values inherit this monotonicity. They are obtained by solving in \(\mu \in R^n\) the optimization problem:

$$\begin{aligned} \text{ min }&\mathop {\sum }\limits _{i=1}^n \left( \mu _i-Y_i\right) ^2 \nonumber \\ \text{ s.t. }&\mu _i \le \mu _{i+1}, \ i=1, \ldots , n-1, \end{aligned}$$
(1)

It can be easily shown that a solution to this problem is a maximum likelihood estimator of the parameters \(\mu _i\), when \(Y_i\) are assumed to be normally distributed with mean \(\mu _i\) and, at the same time, the \(\mu _i\)s are non-decreasing with respect to the predictor.

There exists a simple algorithm, called pool adjacent violators (PAV), that solves problem (1) in O(n) steps [4]. It is widely used due to its computational efficiency, but yet some practitioners are skeptic about using MR in their applications because the fitted response returned by the MR resembles a step function while the expected response in these applications is believed to be continuous and smooth. When there is more than one predictor involved, MR can also be applied, and there are computationally heavy exact algorithms for solving MR problem, such as the algorithm in Maxwell and Muckstadt [25], or computationally inexpensive approximate MR algorithms, such as algorithms in Burdakov et al. [11] and Sysoev et al. [40]. However, the fitted response still resembles a piecewise constant function even in the model with many predictors. Recently, a new generalized additive framework was proposed in Chen and Samworth [12], but when the model has one input, this method returns the same response as the PAV algorithm.

In order to handle the lack of smoothness of the MR, various techniques were developed for the model with one predictor. One group of methods [17, 19, 24, 28] combines the MR approach with kernel smoothers, and the fitted response appears to be monotonic and smooth. A particularly simple ad hoc approach is discussed in Mammen [24], where a smooth monotonic estimator \(m_{\mathrm{IS}}\) first applies the monotonic (called isotonic in Mammen [24]) regression and then a kernel smoother; in another estimator \(m_{\mathrm{SI}}\), the smoothing is followed by the monotonization. Since the complexity of the kernel smoothing is \(O(n^2)\) [16] and the complexity of the MR computation is O(n), the computational cost of \(m_{\mathrm{IS}}\) and \(m_{\mathrm{SI}}\) is \(O(n^2)\). Other methods in this group seem to be more computationally heavy: They either are based on a numerical integration or apply quadratic programming.

Another large group of methods produces a smooth monotonic fit by applying smoothing spline techniques [8, 9, 26, 27, 35, 36, 44]. The quality of the fitting and prediction, as well as computational time of these methods, depends on the number of knots in a spline. If the number of knots (which defines both the complexity and the quality of the model) is fixed, these models are capable to fit quite large data within an acceptable time. However, modern applications often involve data that are large and at the same time are generated by complicated processes. In order to fit such large and complex data, a large number of knots might be needed, which in its turn leads to prohibitively large computational times. We discuss this issue further in Sect. 5. In addition, we include into our simulation studies the method introduced in Pya and Wood [35] (which was shown to be more precise than any of Bollaerts et al. [8], Meyer [26], Meyer [27]).

In the literature, there is also some amount of work based on Bayesian approaches (see for ex. [20, 23, 30, 31, 37, 39, 42]). In general, these methods involve Markov chain Monte Carlo sampling or other type of stochastic optimization, which makes them computationally heavy compared to the aforementioned frequentist alternatives. Complexity and scalability issues are often dismissed or not in the main focus in these papers, and the authors often consider pretty small samples in their simulations. For instance, the method described in Holmes and Heard [20] was presented as ‘extremely fast to simulate,’ and it completes the computations ‘under two minutes’ for a sample size containing around 200 observations. In contrast, the method presented in this paper can fit more than a million observations in less than a minute, as it is illustrated in Burdakov and Sysoev [10]. However, in order to compare the predictive power of these models and our approach, we include in our simulation studies the approach described in Neelon and Dunson [30, 31]. The choice of the method was motivated by the public availability of the code [32], and also by the results of the simulation in Shively et al. [39] demonstrating that there is no obvious winner among the methods in Holmes and Heard [20], Neelon and Dunson [31] and Shively et al. [39]. We have also decided not to include the methods based on Gaussian process optimization (such as [23, 37, 42]) into our simulations because they require at least \(O(n^3)\) numerical operations per iteration, which makes these algorithms too expensive for large data.

The purpose of this work is to develop a method which (a) is fast and well scalable, i.e., able to efficiently handle large data sets and can be efficiently applied in iterative algorithms like GAM or gradient boosting; (b) is statistically motivated rather than ad hoc; (c) enables a user to select a desired degree of smoothness, as it is with splines or kernel smoothers and (d) has a reasonably good predictive power.

For achieving these goals, we modify the MR formulation (1) by penalizing the difference between adjacent fitted response values. This is aimed at eliminating sharp ‘jumps’ of the response function. In this paper, we show that such a simple idea has a rigorous probabilistic background. Our smoothed monotonic regression (SMR) problem is formulated as

$$\begin{aligned} \text{ min }&\mathop {\sum }\limits _{i=1}^n \left( \mu _i-Y_i\right) ^2+\mathop {\sum }\limits _{i=1}^{n-1} \lambda _i\left( \mu _{i+1}-\mu _{i}\right) ^2 \nonumber \\ \text{ s.t. }&\mu _i \le \mu _{i+1}, \ i=1, \ldots , n-1, \end{aligned}$$
(2)

where \(\lambda _i>0\), \(i=1,\ldots ,n-1\), are preselected penalty parameters whose choice is discussed in this paper.

In this work and in an accompanying paper [10], we study problem (2) from different perspectives and present a smoothed pool adjacent violators (SPAV) algorithm that computes the solution of the SMR problem. Paper published by Burdakov and Sysoev [10] is focused on convergence properties given a set of penalty parameters \(\Lambda =\left\{ \lambda _1,\ldots , \lambda _{n-1}\right\} \) and contains the proof of the optimality of the SPAV algorithm from the optimizational perspective. However, the algorithm presented in Burdakov and Sysoev [10] cannot be directly used in machine learning applications. Firstly, the algorithm requires the set \(\Lambda \) to be specified, and if traditional parameter selection, i.e., cross-validation, is used, the overall computational time becomes exponential in n (because at least \(2^{n-1}\) possible \(\Lambda \) need to be considered). Secondly, the algorithm is only able to deliver predictions for the values of the input variables present in the training data; the prediction for all other input values becomes undefined. This is a known limitation of the monotonic regression discussed in Sysoev et al. [41].

The current paper introduces a probabilistic framework that allows for resolving the critical issues mentioned above and thus enables employing the SMR in machine learning applications. In particular, this framework induces a motivated choice for the penalty parameters that reduces the overall worst-case computational cost to \(O(n^2)\). This framework makes it also possible to deliver consistent predictions for the input values that are outside the training data. In addition, we present a technique that performs correction of the boundary inconsistencies. Last but not least, the paper presents numerical analysis of the predictive performance of the proposed model and some alternative algorithms.

The paper is organized as follows. Section 2 presents the SPAV algorithm and also contains estimates of the complexity of this algorithm given a fixed set of \(\Lambda \). In Sect. 3, a probabilistic model inducing the SMR problem is presented, an appropriate choice of the penalty parameters is discussed and a consistent predictive model is presented. In particular, this section introduces a generalized cross-validation for the probabilistic model corresponding to (2). Section 4 considers a problem of inconsistency of the SMR on the boundaries and introduces a correction strategy. In Sect. 5, results of numerical simulations and a comparative study of our smoothing approaches and some alternative algorithms are presented. Section 6 contains conclusions.

2 SPAV algorithm

One can see that the objective function in (2) is strictly convex, because the first term is a strictly convex function and the other one is convex. The constraints are linear. Therefore, the SMR problem (2) is a strictly convex quadratic programming (QP) problem. In principle, it can be solved by the conventional QP algorithms [33]. However, these algorithms do not make use of the special structure of the objective function or constraints in (2), whereas taking this structure into account, as one can see below, allows for substantial speeding-ups. It should also be noted that the general purpose QP algorithms are not of polynomial complexity in contrast to our algorithm.

Owing to the strict convexity of the SMR problem, its solution is unique and it is determined by the Karush–Kuhn–Tucker (KKT) optimality conditions [33]. To derive them, consider the Lagrangian function

$$\begin{aligned} L\left( \mu ,\rho \right) =\sum _{i=1}^n \left( \mu _i-Y_i\right) ^2+\sum _{i=1}^{n-1} \lambda _i\left( \mu _{i+1}-\mu _{i}\right) ^2-\sum _{i=1}^{n-1} \rho _i\left( \mu _{i+1}-\mu _{i}\right) , \end{aligned}$$

where \(\rho \in R^{n-1}\) is the vector of nonnegative Lagrange multipliers. Its first derivative is calculated by the formula

$$\begin{aligned} \nabla _{\mu _i} L\left( \mu ,\rho \right) = \left\{ \begin{array}{ll} 2\left( \mu _1-Y_1\right) +2\lambda _1 \left( \mu _1-\mu _2\right) +\rho _1, &{} i=1,\\ 2\left( \mu _i-Y_i\right) +2\lambda _{i-1}\left( \mu _i-\mu _{i-1}\right) + \\ \quad +2\lambda _i\left( \mu _i-\mu _{i+1}\right) -\left( \rho _{i-1}-\rho _i\right) , &{} i=2, \ldots , n-1,\\ 2\left( \mu _n-Y_n\right) +\\ \quad +\,2\lambda _{n-1} \left( \mu _n-\mu _{n-1}\right) -\rho _{n-1}, &{} i=n. \end{array} \right. \end{aligned}$$
(3)

To represent the KKT conditions in a compact form, we shall use the following notation. Let

$$\begin{aligned} I(a)=\left\{ \begin{array}{ll} 1, &{} \text{ if } a \text{ is } \text{ true },\\ 0, &{} \text{ if } a \text{ is } \text{ false } \end{array}\right. \end{aligned}$$

stand for the indicator function. We denote by \(A\in R^{n \times n}\) and \(B\in R^{n \times (n-1)}\) the matrices whose elements are defined as

$$\begin{aligned} A_{ij}=\left\{ \begin{array}{ll} 1+\lambda _{i-1} I(i>1)+ \lambda _i I(i<n), &{} \text{ if } j=i,\\ -\lambda _{i-1} I(i>1), &{} \text{ if } j=i-1,\\ -\lambda _i I(i<n), &{} \text{ if } j=i+1,\\ 0, &{} \text{ otherwise } \end{array}\right. \end{aligned}$$

and

$$\begin{aligned} B_{ij}=\left\{ \begin{array}{ll} -I(i>1), &{} j=i-1,\\ I(i<n), &{} j=i,\\ 0, &{}\text{ otherwise. } \end{array}\right. \end{aligned}$$

Note that A is a tridiagonal matrix. Denote also \(Y=\left( Y_1,\ldots ,Y_n\right) ^T\).

Using this notation and the formula for \(\nabla _{\mu } L\left( \mu ,\rho \right) \), we can represent the KKT conditions as

$$\begin{aligned}&A\cdot \mu =Y+\frac{1}{2}B\cdot \rho , \end{aligned}$$
(4)
$$\begin{aligned}&\mu _i \le \mu _{i+1}, \quad i=1, \ldots , n-1, \end{aligned}$$
(5)
$$\begin{aligned}&\rho _i\ge 0, \quad i=1, \ldots , n-1, \end{aligned}$$
(6)
$$\begin{aligned}&\rho _i(\mu _{i+1}-\mu _i)=0, \quad i=1, \ldots , n-1. \end{aligned}$$
(7)

The algorithm that we introduce here for solving the SMR problem belongs to the class of dual active set algorithms [7, 18]. At each iteration, it solves the problem

$$\begin{aligned} \text{ min }&\mathop {\sum }\limits _{i=1}^n \left( \mu _i-Y_i\right) ^2+\mathop {\sum }\limits _{i=1}^{n-1} \lambda _i\left( \mu _{i+1}-\mu _{i}\right) ^2 \nonumber \\ \text{ s.t. }&\mu _i = \mu _{i+1}, \ i\in S, \end{aligned}$$
(8)

for a set of active constraints \(S\subseteq \{1,2,\ldots ,n-1\}\). Our algorithm starts with \(S=\emptyset \), enlarging it from iteration to iteration, and terminates when the vector \(\mu \) that solves this problem becomes feasible in the original problem (2).

The correctness of this algorithm is theoretically justified in the accompanying paper [10] which is focused on optimization aspects of our approach. In particular, it is shown in Burdakov and Sysoev [10] that if a constrained optimization problem (8) is solved for some S and the corresponding Lagrange multipliers are all nonnegative, then \(\mu _i = \mu _{i+1}\) for all \(i \in S\) in (2). Moreover, if the optimal solution to problem (8) is such that \(\mu _j \ge \mu _{j+1}\) for some \(j\in S' : S'\notin S\), then \(\mu _j=\mu _{j+1}\) for \(j\in S'\) in (2). These two properties imply that if we set \(S=\emptyset \) and compute all \(j\in S'\) such that \(\mu _j \ge \mu _{j+1}\) , these are active constraints in (2) and thus \(S'\) can be added to S. Because the constraints corresponding to \(S'\) are active in (2), they will also be active in (8), and all Lagrange multipliers in (8) for the current S will be nonnegative. Accordingly, the process of computing of \(S'\) and updating S as

$$\begin{aligned} S \leftarrow S \cup S', S'=\{i\notin S: \ \mu _i \ge \mu _{i+1}\}. \end{aligned}$$
(9)

can be repeated until \(S'\) becomes empty. This will happen when either \(\mu _i < \mu _{i+1}\) for all \(i \notin S\) or S contains all existing constraints from (2). This implies that the algorithm finds the optimal solution to (2) by doing at most n updates of S.

We will show now how to efficiently solve problem (8). Let [i, j] denote a segment of indexes \(\{i,i+1,\ldots ,j-1,j\}\). Suppose that \([p,q-1]\subseteq S\). Then the corresponding adjacent active constraints give \(\mu _p=\mu _{p+1}=\ldots =\mu _{q}\). If, in addition, \(p-1 \not \in S\) and \(q \not \in S\), then we call [p, q] a block. A singleton set \(\{p\}\subseteq [1,n]\) is also called a block if \(p-1 \not \in S\) and \(p \not \in S\). Thus, any active set S generates a partitioning of [1, n] into a set of blocks \(\Omega =\{B_1, B_2, \ldots ,B_{n_B}\}\), where \(n_B\) is the number of blocks. Each block \(B_i=[p_i,q_i]\) is characterized by its number of elements \(n_i=q_i-p_i +1\), its observed mean

$$\begin{aligned} {\bar{Y}}_i=\frac{1}{n_i}\sum _{j=p_i}^{q_i} Y_j \end{aligned}$$

and its common block value\({\hat{\mu }}_i\) such that

$$\begin{aligned} \mu _j = {\hat{\mu }}_i, \quad \forall j\in B_i. \end{aligned}$$
(10)

Denote \({\bar{Y}}=({\bar{Y}}_1, \ldots , {\bar{Y}}_{n_B})^T\) and \({\hat{\mu }}=({\hat{\mu }}_1, \ldots , {\hat{\mu }}_{n_B})^T\). The blocks are supposed to be sorted in increasing order of the indexes they contain, which means that \(p_i - 1 = q_{i-1}\). We denote by \({\hat{A}}\) a \(n_B \times n_B\) tridiagonal matrix whose elements are defined as

$$\begin{aligned} {\hat{A}}_{ij}=\left\{ \begin{array}{ll} 1+\frac{\lambda _{p_i-1}}{n_i} I(p_i>1)+ \frac{\lambda _{q_i}}{n_i} I(q_i<n), &{} \quad \text{ if } j=i,\\ -\frac{\lambda _{p_i-1}}{n_i} I(p_i>1), &{}\quad \text{ if } j=i-1,\\ -\frac{\lambda _{q_i}}{n_i} I(q_i<n), &{}\quad \text{ if } j=i+1,\\ 0, &{}\quad \text{ otherwise. } \end{array}\right. \end{aligned}$$

The next result shows how to easily compute the solution to problem (8).

Theorem 1

The common block values of the optimal solution to problem (8) are uniquely defined by the system of linear equations

$$\begin{aligned} {\hat{A}}\cdot {\hat{\mu }}={\bar{Y}}. \end{aligned}$$
(11)

Proof

As it was mentioned above, the solution to problem (8) is uniquely defined by the system of linear Eq. (4), where (10) holds and \(\rho _i=0\) for all \(i\notin S\). Consider a block \(B_i=[p_i,q_i]\). The corresponding equations in (4) are of the form:

$$\begin{aligned} \left\{ \begin{array}{ll} {\hat{\mu }}_i+\lambda _{j-1}({\hat{\mu }}_i-{\hat{\mu }}_{i-1})\cdot I(j>1) = Y_j -\frac{\rho _{j}}{2} I(j<n) &{} \text{ for } j=p_i\\ {\hat{\mu }}_i= Y_j + \frac{\rho _{j-1}}{2} I(j>1)-\frac{\rho _j}{2} I(j<n) &{} \text{ for } j=p_i+1\\ \cdots \\ {\hat{\mu }}_i +\lambda _j(\hat{\mu _i}-{\hat{\mu }}_{i+1})\cdot I(j<n)=Y_j + \frac{\rho _{j-1}}{2} I(j>1) &{} \text{ for } j=q_i \end{array} \right. \end{aligned}$$

By summing these equations, we obtain

$$\begin{aligned} n_i \hat{\mu _i} + \lambda _{p_i-1}({\hat{\mu }}_i-{\hat{\mu }}_{i-1})\cdot I(p_i>1) +\lambda _{q_i}(\hat{\mu _i}-{\hat{\mu }}_{i+1})\cdot I(q_i<n)= \sum _{j=p_i}^{q_i} Y_j \end{aligned}$$

A simple algebraic manipulation with this equation results in Eq. (11). \(\square \)

The important feature of system (11) is that the matrix \({\hat{A}}\) is tridiagonal. It can be efficiently solved, e.g., by the Thomas algorithm [13] of complexity O(n). Moreover, since \({\hat{A}}\) does not depend on Y, (11) can be viewed as a linear smoother.

We call the outlined algorithm for solving SMR problem (2) a smoothed pool adjacent violators (SPAV) algorithm. It employs Theorem 1.

Algorithm 1

SPAV algorithm

figure c
Fig. 1
figure 1

The solid line is \(f(x)=x\); the circles are artificially generated data \(Y=f(X)+\epsilon \), where \(\epsilon \sim N(0,0.3)\); the dashed line is the SPAV solution (with linear kernel and \(\lambda \) selected by cross-validation, introduced below); the dotted line is the PAV solution

Full size image

Step 3 is called PAV step because it pools adjacent violators, i.e., indexes i and \(i+1\) satisfying \(\mu _i > \mu _{i+1}\) into one set and enforces \(\mu _i=\mu _{i+1}\) in the following steps. The result of the SPAV algorithm and the traditional PAV algorithm is compared in Fig. 1. The step-wise response produced by PAV algorithm can sometimes be unrealistic and deviate substantially from the true model. One can see this in Fig. 1, where the SPAV response looks much more natural and closer to the true model.

The following theorem provides an estimate of the complexity of the SPAV algorithm.

Theorem 2

The complexity of the SPAV algorithm is \(O(n^2)\)

Proof

Smoothing step followed by PAV step can be viewed as one iteration. As it was mentioned above, the number of iterations does not exceed n. The complexity of step 1 is determined by the complexity of composing and solving a tridiagonal system of equations, which is O(n). Step 2 involves O(n) comparison operations. Step 3 involves a search that requires O(n) operations plus adding an element to a list and updating the list of blocks which requires O(n) steps. Therefore, the total complexity of one iteration is O(n), which means that the total complexity of the algorithm is \(O(n^2)\). \(\square \)

Note that the quadratic complexity is a worst-case estimate, which assumes that the number of iterations is n. In practice, we observed that this number was fewer than n, and the CPU time of SPAV algorithm was growing with n much slower than as \(n^2\).

3 Connections to probabilistic modeling

It is a known fact that penalization of the objective can often be thought of putting a regularization prior on the model, as it is for instance with ridge regression and LASSO [29]. We now consider how the problem (2) can be represented from the probabilistic perspective. Assume the following model for the means:

$$\begin{aligned} Y_i \sim N(\mu _i, \alpha ^2), \end{aligned}$$
(12)

where the prior on the components of \(\mu \) are assumed to be of the following form:

$$\begin{aligned}&\mu _{i+1} \sim \mu _i+N_{+}(0, \sigma ^2_i), \ i=1, \ldots , n-1, \end{aligned}$$
(13)
$$\begin{aligned}&p(\mu _1) \propto 1. \end{aligned}$$
(14)

Here \(N_+\) is the truncated normal distribution that ensures that the sequence of \(\mu _i\)’s is non-decreasing and \(\sigma _i^2\). The constants \(\sigma ^2_i\) can be arbitrarily chosen but since we assume that the expected response should be a continuous function, it is natural to let \(\sigma ^2_i\) depend on how close \(X_{i+1}\) is to \(X_i\): The smaller the distance, the lesser the variance should be; and when \(X_{i+1}=X_i\), \(\sigma ^2_i\) should be zero.

We introduce a family of functions K, called here kernel (by analogy to the Gaussian Process model), which meet the requirements mentioned above and are defined by

$$\begin{aligned} \sigma _i^2=\frac{1}{\beta K\left( X_i, X_{i+1}\right) }, \end{aligned}$$
(15)

where, for instance,

$$\begin{aligned} K(X,X')=\frac{1}{\left| X-X'\right| ^p}. \end{aligned}$$
(16)

Here \(\beta \) is some constant that steers the level of smoothness: The higher the \(\beta \), the lesser the variance is and the higher is the degree of smoothness; p is a constant that also steers the flexibility of the model: Higher p allows for larger variation between the nearest points. We shall call the function K, for \(p=1\) and \(p=2\), a linear kernel and \(p=2\)quadratic kernel, respectively. In principle, one may select some expression for the kernel \(K(X,X')\) other than (16); the important is that this function should be non-decreasing with respect to \(\left| X-X'\right| \), and \(1/K(X,X')\) should become zero for \(X=X'\).

An important property of our model is presented in the following result.

Theorem 3

The solution to problem (2), where

$$\begin{aligned} \lambda _i=\frac{\alpha ^2}{\sigma _i^2}, \quad i=1, \ldots \,n-1, \end{aligned}$$
(17)

is the maximum a posteriori estimate provided by model (12)–(14).

Proof

According to Bayes theorem, the posterior distribution is

$$\begin{aligned} p(\mu |Y,X) \propto p(Y|\mu ,X)\cdot p(\mu |X). \end{aligned}$$

Here, the likelihood is the product of normal distributions

$$\begin{aligned} p(Y|\mu ,X) \propto \mathrm{exp}\left( -\frac{\mathop {\sum }\nolimits _{i=1}^n (Y_i-\mu _i)^2}{2 \alpha ^2}\right) . \end{aligned}$$

The prior \(p(\mu |X)\) can be computed via the chain rule:

$$\begin{aligned} p(\mu |X)=p(\mu _1|X) \prod _{i=1}^{n-1} p(\mu _{i+1}|\mu _i , X). \end{aligned}$$

Taking into account that \(\mu _i \le \mu _{i+1}\) for all \(i=1,\ldots , n-1\), we have

$$\begin{aligned} p(\mu |X) \propto \mathrm{exp}\left( -\frac{\mathop {\sum }\nolimits _{i=1}^{n-1} \left( \mu _{i+1}-\mu _i\right) ^2}{2 \sigma _i^2}\right) =\mathrm{exp}\left( - 1/(2\alpha ^2) \sum _{i=1}^{n-1} \lambda _i \left( \mu _{i+1}-\mu _i\right) ^2\right) , \end{aligned}$$

where \(\lambda _i\) is defined by (17).

By computing the product of the likelihood and the prior, and then taking the logarithm, we get

$$\begin{aligned} \mathrm{log}\ p(\mu |Y,X) \propto -\sum _{i=1}^n (Y_i-\mu _i)^2-\sum _{i=1}^{n-1} \lambda _i \left( \mu _{i+1}-\mu _i\right) ^2, \end{aligned}$$

which implies that the maximum of \(p(\mu |Y,X)\) is assured by the solution to problem (2). \(\square \)

Using this theorem and assuming that the variance is given by (15), we obtain

$$\begin{aligned} \lambda _i=\frac{\alpha ^2}{\sigma _i^2}=\lambda K(X_i, X_{i+1}), \end{aligned}$$
(18)

where \(\lambda =\alpha ^2 \cdot \beta \). Given that the noise variance \(\alpha ^2\) is fixed, the smoothing parameter \(\lambda \) plays the same role as \(\beta \): The higher \(\lambda \) is, the greater is the degree of smoothness of the fitted SPAV response.

For the kernel defined by (16) with \(p=2\), formula (18) indicates that the penalty terms in (2) takes the form

$$\begin{aligned} \lambda _i (\mu _{i+1}-\mu _i)^2 = \lambda \left( \frac{\mu _{i+1}-\mu _i}{X_{i+1}-X_i}\right) ^2. \end{aligned}$$

Then, in this case, smoothing is performed by penalizing the squared slope of the expected response where the slope is computed by using a finite-difference approximation.

Our analysis enables us to conclude that, using the probabilistic approach, it is possible to select an appropriate structure of \(\lambda _i\) in such a way that it reflects the location of the X components. Without using probabilistic modeling, this structure would perhaps be difficult to determine. Another advantage of using probabilistic methodology is that it provides a strategy for determining consistent predictions for some new values of X, as it is discussed below.

Prediction for monotonic regression is a special problem, as it is discussed in Sysoev et al. [41].

In general, the MR is only able to compute unique predictions for the values of the input levels that are present in the training data. This can be a critical obstacle for applying MR in many machine learning applications. However, for the smoothed MR, we can define a consistent prediction model for some new predictor value \(X^*\) as follows.

Consider the following model for the expected response \(\mu ^*\) that corresponds to a predictor value \(X^*\) which is located between \(X_i\) and \(X_{i+1}\):

$$\begin{aligned}&\mu ^*|\mu _i \sim \mu _i +N_+(0, \sigma _{i,*}^2), \end{aligned}$$
(19)
$$\begin{aligned}&\mu _{i+1}|\mu ^* \sim \mu ^*+N_+(0,\sigma _{*, i+1}^2), \end{aligned}$$
(20)

where the \(\sigma \) values are defined by (15) in which variables \((X_i,X_{i+1})\) are substituted by \((X_i,X^*)\) or \((X^*,X_{i+1})\), respectively. If \(X^*\) is outside the observed interval, i.e., \(X^* >X_n\) or \(X^*<X_1\), then we simply define the predicted value for \(\mu ^*\) as \(\mu _n\) or \(\mu _1\), respectively.

The prediction model presented by (19) and (20) is a natural extension of the model given by (13) because the two models have the same structure. Accordingly, we can derive the prediction in the same way as it was done for (13), i.e., by computing a maximum a posteriori estimate of \(\mu ^* | \mu _i, \mu _{i+1}\).

Theorem 4

Given model (19), (20), the maximum a posteriori estimate of \(\mu ^* | \mu _i, \mu _{i+1}\) can be computed as

$$\begin{aligned} \mu ^*=\frac{K(X_i, X^*)\mu _i + K(X^*, X_{i+1})\mu _{i+1}}{K(X_i, X^*)+K(X^*, X_{i+1})}. \end{aligned}$$
(21)

Proof

By Bayes formula and the chain rule, we get:

$$\begin{aligned} p(\mu ^* | \mu _i, \mu _{i+1})=\frac{p(\mu ^* , \mu _i, \mu _{i+1})}{p(\mu _i, \mu _{i+1})}=\frac{p(\mu _i)}{p(\mu _i, \mu _{i+1})} p(\mu ^*|\mu _i)p(\mu _{i+1}|\mu ^*). \end{aligned}$$

Therefore,

$$\begin{aligned} \mathrm{log} p(\mu ^* | \mu _i, \mu _{i+1}) \propto -\frac{(\mu ^*-\mu _i)^2}{2 \sigma _{i,*}^2}-\frac{(\mu _{i+1}-\mu ^*)^2}{2 \sigma _{*, i+1}^2}. \end{aligned}$$

By maximizing the expression above and using (15), we get

$$\begin{aligned} 2\beta K(X_i, X^*)(\mu ^*-\mu _i)+2\beta K(X^*, X_{i+1})(\mu ^*-\mu _{i+1})=0, \end{aligned}$$

which leads to (21). \(\square \)

From the practical machine learning perspective, it is crucial that instead of optimizing \(n-1\) parameters in (2), we need to estimate only one parameter \(\lambda \). A possible way of doing this is cross-validation. The standard cross-validation implies that several \(\lambda \) values need to be considered, and the SMR needs to be computed for each \(\lambda \) value. This leads to the overall computational time \(O(n^2)\) (because the number of considered \(\lambda \) values is normally smaller than n and is not dependent on n). However, applying the cross-validation may still be computationally expensive.

We suggest a procedure called here generalized cross-validation. It is based on the following idea supported by empirical observations. The expected (true) response should normally be increasing, and there is a little chance of observing a region where the response is constant. Since in our model the response is constant for the observations that were merged into one block by the PAV step of the SPAV algorithm, we can conclude that in an ideal model there should be very few executions of the PAV step. Accordingly, if we remove the PAV steps from this algorithm, it should not affect much this ideal model, although the monotonicity may be violated. The algorithm can be presented as follows.

Algorithm 2

Smoothing algorithm

figure d
Fig. 2
figure 2

An artificially generated data \(Y=f(X)+\epsilon , \epsilon \sim N(0,0.3)\) where the solid line is \(f(x)=x^2\), the dashed line is the response obtained by the SPAV algorithm (cross-validated, linear kernel) and Smoothing algorithm with the same \(\lambda \) as in the SPAV algorithm (dotted line)

Full size image

The fitted responses produced by the SPAV and Smoothing algorithms are presented in Fig. 2, which demonstrates that these responses are quite similar.

We define the generalized cross-validation as a standard cross-validation in which Algorithm 2 is applied instead of Algorithm 1 in order to determine an optimal penalty \(\lambda \). This strategy allows for substantially reducing the computational time. Our numerical experiments confirm that the local optimum of the cross-validation curve and the generalized cross-validation curves are typically located close to each other, as it is illustrated in Fig. 3.

Fig. 3
figure 3

Cross-validation curve (solid) and the generalized cross-validation scores (dashed) for some artificially generated data, \(n=100\)

Full size image

4 Correction on the boundaries

The MR is known to be inconsistent on the boundaries, which means that the MR estimates for \(\mu _1\) and \(\mu _n\) do not converge to the true values when n tends to infinity, and some solutions to this problem were suggested [34, 43]. This problem is also known as the spiking problem. An intuitive explanation of this issue is the asymmetry of the PAV algorithm on the boundary: The observation with index n can only be merged into a block with the observations \(i<n\), while the observation with index j located in the middle of the domain of X can be merged into a block with neighbors \(i>j\) and \(i<j\). It may happen that \(Y_n>Y_i\) for all \(i<n\). In this case, the PAV algorithm does not make any error correction and returns \({\hat{\mu }}_n=Y_n\).

A similar kind of asymmetry can be observed in the SMR problem: The objective function in (2) contains two penalty factors (involving \(i+1\) and \(i-1\)) for all \(i=2, \ldots , n-1\), while for \(i=n\) or \(i=1\) there is only one penalty factor. Figure 1 demonstrates that the SPAV fitted response can sometimes behave badly on the boundaries, i.e., it can be shifted toward the observed values of \(Y_1\) and \(Y_n\).

In order to resolve this issue, we apply the idea presented in Wu et al. [43]. More specifically, we add two extra terms aimed at penalizing too high values of \(\mu _n\) and too low values of \(\mu _1\):

$$\begin{aligned} \text{ min }&\mathop {\sum }\nolimits _{i=1}^n \left( \mu _i-Y_i\right) ^2+\mathop {\sum }\nolimits _{i=1}^{n-1} \lambda _i\left( \mu _{i+1}-\mu _{i}\right) ^2+ \phi \mu _n - \phi \mu _1 \nonumber \\ \text{ s.t. }&\mu _i \le \mu _{i+1}, \ i=1, \ldots , n-1, \end{aligned}$$
(22)

where \(\phi >0\) is a penalty factor.

It can be easily verified that

$$\begin{aligned} (\mu _1 - Y_1)^2 + (\mu _n - Y_n)^2 + \phi \mu _n - \phi \mu _1 = \left( \mu _1 - Y_1 - \frac{\phi }{2}\right) ^2 + \left( \mu _n - Y_n + \frac{\phi }{2}\right) ^2 + c, \end{aligned}$$

where c does not depend on \(\mu _1\) or \(\mu _n\). Like in Wu et al. [43], this observation allows for reducing problem (22) to (2) by shifting the first and the last observed response values as follows:

$$\begin{aligned} Y_1 \leftarrow Y_1 + \frac{\phi }{2} \quad \text{ and } \quad Y_n \leftarrow Y_n - \frac{\phi }{2}. \end{aligned}$$

Then problem (2) modified in this way can be solved by means of the SPAV algorithm. The only requirement is to use the values \(Y'=Y+\phi \cdot e\) instead of Y, where \(e=(1/2, 0,\ldots , 0, -1/2)^T\).

Consider now how to choose the parameter \(\phi \). One possibility is to use cross-validation, as it was suggested for \(\lambda \). However, selecting an optimal combination of two parameters might be computationally expensive, and we describe an alternative approach that appeared to work well in practice.

The SPAV algorithm solves problem (11) repeatedly, and if Y is replaced by \(Y'\), the equation becomes

$$\begin{aligned} {\hat{A}}\cdot {\hat{\mu }}=\bar{Y'}={\bar{Y}}+\phi {\bar{e}}, \end{aligned}$$
(23)

that is

$$\begin{aligned} {\hat{\mu }}={\hat{A}}^{-1}{\bar{Y}}+\phi {\hat{A}}^{-1}{\bar{e}}, \end{aligned}$$
(24)

where \({\bar{e}}=\left( \frac{1}{2 n_1}, 0,\ldots , 0,\frac{-1}{2 n_m}\right) \), and \(n_1\) and \(n_m\) are sizes of blocks 1 and \(m=n_B\), respectively. We suggest to select \(\phi \) in such a way that \({\hat{\mu }}={\hat{\mu }}(\phi )\) approximates the observed data \({\bar{Y}}\) in the best way in the least-squares sense:

$$\begin{aligned} \min _{\phi } ({\hat{\mu }}(\phi )-{\bar{Y}})^T ({\hat{\mu }}(\phi )-{\bar{Y}}). \end{aligned}$$

This yields the optimal estimate

$$\begin{aligned} {\hat{\phi }}=\frac{({\bar{Y}}-\mu ')^T e'}{\Vert e'\Vert ^2}, \end{aligned}$$

where \(\mu '={\hat{A}}^{-1}{\bar{Y}}\) and \(e'={\hat{A}}^{-1}{\bar{e}}\). Therefore, the fitted value \({\hat{\mu }}\) at each Smoothing Step of the SPAV algorithm can be computed as follows:

Algorithm 3

Step 1 of SPAV with correction

figure e

Note that the linear equations in Algorithm 3 involve tridiagonal matrices only, and the rest of the algorithm contains simple vector operations. Therefore, the complexity of computing the correction is O(n), and the overall \(O(n^2)\) complexity of the SPAV algorithm is not affected by introducing the correction.

5 Numerical results

Modern machine learning methods are often required to process large and complex data, and this needs to be taken into account when examining the performance of the fitting methods. In order to evaluate the efficiency of the proposed smoothing approach, we compared it to the following methods:

  • monotonic smoothers \(m_{\mathrm{IS}}\) and \(m_{\mathrm{SI}}\) described in Mammen [24],

  • PAV solution \(m_{\mathrm{PAV}}\),

and to two more recent methods:

  • shape constrained additive models (SCAM), described in Pya and Wood [35],

  • Bayesian isotonic regression (BIR), introduced in Neelon and Dunson [30] and Neelon and Dunson [31].

The former two methods have a fixed complexity estimate, which is \(O(n^2)\), while the performance of the two latter methods depends on the number of knots.

Intuition dictates that the number of knots in a model should be dependent on the complexity of the underlying data generating process, and it was confirmed by our preliminary simulations. We considered data sets for various values of n and response \(Y=X+\mathrm{sin}(X)+\epsilon \), where \(X\sim U[0,\left\lfloor n/3\right\rfloor ]\) and \(\epsilon \sim N(0,1)\). It is obvious that both the size and complexity of the data increase with n. It appeared that in order to capture the features of the underlying data, it was necessary for the BIR and SCAM methods to increase the number of knots in proportion to n. Figure 4 represents one such case.

Fig. 4
figure 4

Data were generated as \(X\sim U[0,50]\), \(Y=X+\mathrm{sin}(X)+\epsilon \), \(\epsilon \sim N(0,1), \hbox {N}=150\). The top panel: data are fit by SPAV (dotted line), SCAM with 40 knots (light curve) and SCAM with 80 knots (dark curve). The bottom panel: data are fit by SPAV (dotted line), BIR with 5 knots (light curve) and BIR with 30 knots (dark curve). Both figures are zoomed to \(X \in [0,25]\). Both panels demonstrate a clear underfitting of SCAM and BIR when the amount of knots is not sufficient

Full size image

In order to study how BIR and SCAM methods perform in case of large and complex data, i.e., when both size and complexity of the data increase, we performed simulations where data were generated according to the model above, and the number of knots was selected as \(k=n/2\) for SCAM and \(k=n/5\) for BIR, and each model was generated 100 times. Tables 1 and 2 demonstrate the CPU time averaged over model instances. By applying a polynomial regression to these results, it can be concluded that the complexity grows in practice faster than quadratically with n for these approaches. By extrapolating the results, it can be concluded that for \(n=100{,}000\) observations and the settings described above the SCAM algorithm will take approximately 6 days while the BIR algorithm will require approximately 220 days. Accordingly, it can be prohibitively expensive to fit large and complex data by these methods if a high quality of prediction is required. In contrast, the computational complexity of the SPAV method is only dependent on the amount of observations, and its practical complexity grows almost linearly with n [10]. For the aforementioned model with \(n=100{,}000\), the SPAV algorithm takes less than a minute.

Table 1 Computational time (s) for SCAM algorithm with a number of knots increasing with n
Full size table
Table 2 Computational time (s) for BIR algorithm with a number of knots increasing with n
Full size table

Our comparative simulation studies involve the data generated as \(X \sim U[0,A]\), \(Y=f(X)+\epsilon \), \(\epsilon \sim N(0,s)\) for all combinations of the following settings: \(n=100, 1000\) or 10, 000; \(s=0.03\) or 0.1, the functional shape f is one of the following functions \(f_1(X)=X\), \(f_2(X)=X^2\), \(f_3(X)=(X+\mathrm{sin}(X))/10\), \(f_4(X)=\mathrm{tanh} \left( \frac{n}{10} (X-0.5) \right) \), and \(A=\left\lfloor n/5\right\rfloor \) when \(f_3\) is used and \(A=1\) otherwise. These functions were chosen in order to represent various possible behaviors of the underlying model such as linearity, nonlinearity, increasing complexity or a sudden level shift. The latter property is dismissed by many methods although the change points are often present in machine learning applications. To measure the uncertainty of our results, we generate \(M=100\) instances for the same model.

Each data set generated in our simulations was processed by:

  • \(m_{1}\): SPAV algorithm with linear kernel with correction where \(\lambda \) was selected by the generalized cross-validation with 10 folds,

  • \(m_{2}\): SPAV algorithm with linear kernel with correction where \(\lambda \) was selected by the cross-validation with 10 folds,

  • \(m_{3}\): SPAV algorithm with quadratic kernel without correction where \(\lambda \) was selected by the generalized cross-validation with 10 folds,

  • \(m_{4}\): SPAV algorithm with linear kernel without correction where \(\lambda \) was selected by the generalized cross-validation with 10 folds.

  • \(m_{\mathrm{SCAM}}\): SCAM algorithm. Due to time limitations, we fixed \(k=15\) as it was done in the R package documentation of SCAM.

  • \(m_{\mathrm{BIR}}\): BIR algorithm. Due to time limitations, we fixed \(k=3\) as it was recommended in Neelon and Dunson [30].

  • monotonic smoothers \(m_{\mathrm{IS}}\) and \(m_{\mathrm{SI}}\),

  • monotonic regression \(m_{\mathrm{PAV}}\),

The mean squared error (which is a measure of the predictive performance)

$$\begin{aligned} \mathrm{MSE}=\frac{1}{n}\sum _{i=1}^n \left( m_{*}(X_i)-f(X_i)\right) ^2 \end{aligned}$$

is computed, where \(m_{*}\) is a fitted response computed by some method. The average MSE values computed for different settings are presented in Table 3. Standard errors \(se\left( {\overline{\mathrm{MSE}}}\right) \) for each average MSE value \({\overline{\mathrm{MSE}}}\) were computed from the set of the MSE values \(\left\{ \mathrm{MSE}_1,\ldots , \mathrm{MSE}_M\right\} \) as

$$\begin{aligned} \mathrm{se}\left( {\overline{\mathrm{MSE}}}\right) =\frac{1}{M}\sqrt{\sum _{i=1}^M (\mathrm{MSE}_i-{\overline{\mathrm{MSE}}})^2}, \end{aligned}$$

where M is the amount of instances generated per model. The standard errors are given in Table 4.

By analyzing MSE values, it can be concluded that the SPAV algorithm has two main competitors: the SCAM algorithm and the PAV algorithm. The other tested algorithms appear to have a worse predictive performance than one of these three algorithms.

When the underlying model is simple, i.e., when it is given by functions \(f_1\) or \(f_2\), the average MSE of the SCAM algorithm is smaller than the average MSE values of all other algorithms, including SPAV. However, it must be noted that the SPAV algorithm is ranked second for these cases, and its MSE values are often quite close to those of the SCAM algorithm. Moreover, for some settings the difference is not statistically significant.

When the underlying model is complex or has sharp level shifts (change points), the average MSE values of the SCAM algorithm are quite high even for small n values, and the predictive performance dramatically decreases for large n values. For such underlying models, the SPAV algorithm is significantly more precise than the SCAM algorithm. Our results demonstrate that the SPAV algorithm has the lowest MSE values for these underlying models, while the PAV algorithm is ranked second, and the difference in predictive performance between these two algorithms is statistically significant.

By comparing the variants of the SPAV algorithm in Table 3, it can be concluded that applying the boundary correction often helps to improve the predictive power of the algorithm, and the effect is quite substantial for simpler models. It appears that applying generalized cross-validation instead of the usual cross-validation often leads to similar MSE values, which was expected due to the results presented in Sect. 3. Results presented in the table also indicate that employing a linear kernel seems to lead to a better predictive performance than using a quadratic kernel.

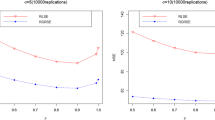
In order to further investigate the performance of the SPAV approach, we consider two real datasets: ‘Gas sensor’ data [15] (containing around 4 million observations) and ‘Geo-Magnetic field’ data [6] (containing around fifty thousand observations). The datasets were downloaded from UCI Machine Learning repository [3]. Figures 5 and 6 demonstrate measurements of a pair of sensors for samples of \(n=10^4\) observations extracted from these datasets. Both figures lead to the conclusion that relationship between the corresponding sensors is reasonable to model as a monotonic function. We fit models \(m_1\) and \(m_{\mathrm{SCAM}}\) (which appear to be the main competitors in our simulation studies) to these samples by taking ‘Sensor 15’ as X variable and ‘Sensor 18’ as Y variable in the ‘Gas sensor’ data and ‘Acceleration X sensor’ as X variable and ‘Y-axis angle roll sensor’ as Y variable in ‘Geo-Magnetic field’ data. The predictions from the fitted models are shown in Figures 5 and 6 as solid lines.

Fig. 5
figure 5

A sample of \(n=10^4\) observations from the ‘Gas sensor’ data fitted by \(m_1\) model (left panel) and by \(m_{\mathrm{SCAM}}\) model (right panel)

Full size image
Fig. 6
figure 6

A sample of \(n=10^4\) observations from the ‘Geo-magnetic field’ data fitted by \(m_1\) model (left panel) and by \(m_{\mathrm{SCAM}}\) model (right panel)

Full size image

To make a comparison of the predictive performance of \(m_1\) and \(m_{\mathrm{SCAM}}\), we apply the following procedure to each of the two datasets. In step 1, we sample (non-overlapping) training and test data of the size \(n=10^4\) from the given dataset. In step 2, we fit \(m_1\) and \(m_{\mathrm{SCAM}}\) to the training data (in model \(m_1\), the generalized cross-validation is applied to the current training data) and compute the MSE values for the test data. Steps 1 and 2 are repeated \(M=100\) times, and the obtained set of the MSE values is used to compute the mean MSE value and the standard error of the mean MSE for both models. Table 5 illustrates the results. In addition, we compute the test errors by sampling \(n=10^5\) observations from the ‘Gas sensor’ data and fitting \(m_1\) and \(m_{\mathrm{SPAV}}\) models. The test error for \(m_1\) is \(29.09\times 10^{-3}\) while for \(m_{\mathrm{SCAM}}\) it is \(30.85 \times 10^{-3}\).

It can be concluded from the presented analysis of real datasets that \(m_1\) has a statistically significantly better performance than \(m_{\mathrm{SCAM}}\) for these data. A possible explanation for this result can be that \(m_1\) model is flexible enough to discover small but significant trends in the data which are not discovered by \(m_{\mathrm{SCAM}}\)(as Fig. 5 illustrates), and \(m_1\) is better than \(m_{\mathrm{SCAM}}\) in modeling sharp level shifts (as Fig. 6 illustrates).

6 Conclusions

In this work, we introduce an approach for smoothed monotonic regression in one predictor variable. It allows for adjusting the degree of smoothness to the data. We have shown that the worst-case computational complexity of this method is \(O(n^2)\) which makes the method suitable in large-scale settings. Moreover, it is found in the accompanying paper [10] that, in practice, its running time grows almost linearly with n for a given set of penalty factors \(\Lambda \).

In many machine learning applications, the dependence between the response and predictor variables is a complicated function. Our numerical experiments demonstrate that the predictive performance of SCAM and BIR methods can substantially degrade when the complicated data are involved, unless a sufficiently large amount of knots is used. At the same time, it may be impossible to choose a proper number of knots in these algorithms without making them prohibitively too expensive. The SMR method is free of this shortcoming. Our simulations demonstrate that, in these settings, the SMR method has the best predictive performance compared to the other tested algorithms. It should be emphasized that the computational cost of the our approach does not depend on the complexity of the underlying response function.

Another obvious advantage of the SMR method is that it is able to treat both smooth or non-smooth responses: For small values of the smoothing parameter, a response close to piecewise-constant is produced, and the increasing smoothing parameter value increases the degree of smoothness. Our numerical experiments reveal that our approach has a superior predictive performance in situations when there is a sharp change in the level in the response function, and that is important for the applications characterized by the presence of change points.

The SMR problem was introduced as a regularization problem with n regularization parameters. Then, a connection to a probabilistic model was established which assured the same MAP estimate as the solution to the regularization problem. The probabilistic formulation provided us with a clear strategy for reducing n regularization parameters to just one parameter by properly setting the structure of the prior variance and thus reducing the overall worst-case computational cost to \(O(n^2)\). The prior variance depends on the kernel structure, and the predictive performance was better when linear kernels were used compared to the case with quadratic kernels. In addition, the probabilistic formulation provided us with a consistent predictive model for the input values which are not present in the training data. Further, we motivated a generalized cross-validation strategy for the selection of the smoothing parameter. Our preliminary experiments confirmed that the generalized cross-validation produces results which are similar to the cross-validation, and these required far less computational efforts. Finally, a boundary effect problem was studied, and a strategy for the inconsistency correction was suggested. The proposed strategy had a clear positive effect on the predictive performance of the SMR method.

For estimating the predictive performance of the SMR method, it was natural to use MSE values (as we have done in our numerical experiments). For practical data, measures of uncertainty, such as confidence (credible) limits, can also be derived. A natural way of deriving such intervals would be to use the probabilistic formulation (12) and derive the posterior distribution of the quantity of interest, but this would require a full Bayesian inference for this model. This is avoided in our scalable algorithms. An alternative (which we recommend) is to use bootstrap techniques [14] together with the estimator provided by the result of Algorithms 1 or 3.

Some peculiarities of our model are noteworthy. First, although the fitted response is continuous, it is in general not differentiable. This is because the predictive model uses only two adjacent fitted values to make prediction for a new input value, and this may result in that the left and right derivatives of the fitted response may be different in some points. Another peculiarity is that the fitted response and the prediction depend on the choice of the kernel, but this is also typical for many other methods, such as kernel smoothers.

The SMR problem was formulated for the case of one predictor variable, and one can directly use our model in a generalized additive model setting to fit the models with many predictors. Another possible way of fitting multivariate data could be to generalize our frequentist model as follows:

$$\begin{aligned} \text{ min }&\mathop {\sum }\limits _{i=1}^n \left( \mu _i-Y_i\right) ^2+\mathop {\sum }\limits _{j,k} \lambda _{jk}\left( \mu _{j}-\mu _{k}\right) ^2 \\ \text{ s.t. }&\mu _j \le \mu _{k}, \ \text{ iff } \ X_j \preceq X_k \ \forall j,k=1, \ldots , n \end{aligned}$$

For small n, the corresponding quadratic programming problem can be solved by using conventional optimization algorithms, but for large n, these algorithms are prohibitively expensive. Finding efficient ways of solving this problem is a direction of our future research. Another interesting direction is to state a joint fitted and predictive model and then perform its full Bayesian analysis.