Abstract
Accuracy of the k-nearest neighbour (\(k\hbox {NN}\)) classifier depends strongly on the ability of the used distance to induce k-nearest neighbours of the same class while keeping distant samples of different classes. For time series classification, \(k\hbox {NN}\) based on dynamic time warping (dtw) measure remains among the most popular and competitive approaches. However, by assuming time series uniformly distributed, standard dtw may show some limitations to classify complex time series. In this paper, we show how to enhance the potential of \(k\hbox {NN}\) under time warp measure by learning a locally weighted dynamic time warping. For that, first discriminative features are learned from the neighbourhoods, then used to weight time series elements to bring closer the k-nearest neighbours of the same class and move away the k-nearest neighbours of different classes. To evaluate the proposed method, a deep analysis and experimentation are conducted on 87 public datasets from different application domains, varying sizes and difficulty levels. The results obtained show significant improvement in the proposed weighted dtw for time series \(k\hbox {NN}\) classification.







Similar content being viewed by others
Notes
i.i.d.: Independent and Identically Distributed.
All the obtained results can however be directly extended to multivariate time series, possibly of different lengths, as the temporal alignments, at the core of the measures we consider, can be defined in those cases as well.
UMD and BME are available at http://ama.liglab.fr/~douzal/tools.html, the rest of the data at http://www.cs.ucr.edu/~eamonn/time_series_data/.
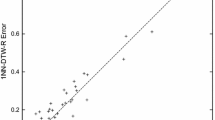
Results for some very large datasets are missing for the costly \({{\textsc {dtw}}}_{{{\textsc {lm}}}}\) due to the huge required time consumption.
References
Abraham Z, Tan P (2010) An integrated framework for simultaneous classification and regression of time-series data. In: SIAM International Conference on Data Mining, pp. 653–664
Bagnall A, Lines J, Bostrom A, Large J, Keogh E (2017) The great time series classification bake off: a review and experimental evaluation of recent algorithmic advances. Data Min Knowl Disc 31(3):606–660
Batista GE, Wang X, Keogh EJ ( 2011) A complexity-invariant distance measure for time series. In: SDM, vol. 11, SIAM, pp. 699–710
Bellet A, Habrard A, Sebban M (2015) Metric learning. Synthesis Lectures on Artificial Intelligence and Machine Learning 9(1):1–151
Berndt DJ, Clifford J (1994) Using dynamic time warping to find patterns in time series. In: KDD Workshop, vol. 10, Seattle, WA, pp 359–370
Caiado J, Crato N, Pena D (2006) A periodogram-based metric for time series classification. Comput Stat Data Anal 50:2668–2684
Chen Y, Keogh E, Hu B, Begum N, Bagnall A, Mueen A, Batista G (2015) The ucr time series classification archive. www.cs.ucr.edu/ eamonn/time_series_data/
Cover TM, Hart PE (1967) Nearest neighbor pattern classification. IEEE Trans Inf Theory 13(1):21–27
Davis JV, Kulis B, Jain P, Sra S, Dhillon IS ( 2007) Information-theoretic metric learning. In: Proceedings of the 24th international conference on Machine learning, ACM, pp 209–216
Demšar J (2006) Statistical comparisons of classifiers over multiple data sets. J Mach Learn Res 7:1–30
Díaz SP, Vilar JA (2010) Comparing several parametric and nonparametric approaches to time series clustering: a simulation study. J Classif 27(3):333–362
Dietterich TG (1998) Approximate statistical tests for comparing supervised classification learning algorithms. Neural Comput 10(7):1895–1923
Do C-T, Douzal-Chouakria A, Marié S, Rombaut M (2015) Temporal and frequential metric learning for time series knn classification, In: Proceedings of the 1st international conference on advanced analytics and learning on temporal data-vol 1425, CEUR-WS. org, pp 35–41
Do C-T, Douzal-Chouakria A, Marié S, Rombaut M, Varasteh S (2017) Multi-modal and multi-scale temporal metric learning for a robust time series nearest neighbors classification. Inf Sci 418:272–285
D’Urso P, Maharaj E (2009) Autocorrelation-based fuzzy clustering of time series. Fuzzy Sets Syst 160(24):3565–3589
Frambourg C, Douzal-Chouakria A, Gaussier E (2013) Learning multiple temporal matching for time series classification. In: Tucker A, Höppner F, Siebes A, Swift S (eds) Intelligent data analysis. London, pp 198–209
Garreau D, Lajugie R, Arlot S, Bach F (2014) Metric learning for temporal sequence alignment. In: Advances in neural information processing systems, pp 1817–1825
Gaudin R, Nicoloyannis N (2006) An adaptable time warping distance for time series learning. In: The 5th International Conference on Machine Learning and Applications, pp 213–218
Itakura F (1975) Minimum prediction residual principle applied to speech recognition. IEEE Trans Acoust Speech Signal Process 23(1):67–72
Jeong Y, Jeong M, Omitaomu O (2011) Weighted dynamic time warping for time series classification. Pattern Recognit 44:2231–2240
Kakizawa Y, Shumway RH, Taniguchi M (1998) Discrimination and clustering for multivariate time series. J Am Stat Assoc 93(441):328–340
Keogh EJ, Pazzani MJ (2001) Derivative dynamic time warping., In: SDM, vol. 1, SIAM, pp. 5–7
Kruskall J, Liberman M (1983) The symmetric time warping algorithm: From continuous to discrete. In: Time Warps, string edits and macromolecules. Addison-Wesley
Kulis B (2012) Metric learning: a survey. Found Trends Mach Learn 5(4):287–364
Montero P, Vilar J (2014) TSclust: an R package for time series clustering. J Stat Softw 62(1):1–43
Nicolae M-I, Gaussier É, Habrard A, Sebban M (2016) Similarity learning for time series classification, arXiv preprint arXiv:1610.04783
Rabiner L (1989) A tutorial on hidden markov models and selected applications in speech recognition. Proc IEEE 77(2):257–286
Rakthanmanon T, Campana B, Mueen A, Batista G, Westover B, Zhu Q, Zakaria J, Keogh E (2012) Searching and mining trillions of time series subsequences under dynamic time warping, In: Proceedings of the 18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. ACM, pp 262–270
Ratanamahatana CA, Keogh E (2004) Making time-series classification more accurate using learned constraints. In: SIAM international conference on data mining, pp 11–22
Rydell J, Borga M, Knutsson H (2008) Robust correlation analysis with an application to functional MRI. In: IEEE international conference on acoustics, speech and signal processing, 453–456
Sahidullah M, Saha G (2012) Design, analysis and experimental evaluation of block based transformation in MFCC computation for speaker recognition. Speech Commun 54(4):543–565
Sakoe H, Chiba S (1978) Dynamic programming algorithm optimization for spoken word recognition. IEEE Trans Acoust Speech Signal Process 26(1):43–49
Salvador S, Chan P (2004) Fastdtw: Toward accurate dynamic time warping in linear time and space. In: KDD workshop on mining temporal and sequential data. Citeseer
Soheily-Khah S, Douzal-Chouakria A, Gaussier E (2016) Generalized k-means-based clustering for temporal data under weighted and kernel time warp. Pattern Recognit Lett 75:63–69
Tormene P, Giorgino T, Quaglini S, Stefanelli M (2009) Matching incomplete time series with dynamic time warping: an algorithm and an application to post-stroke rehabilitation. Artif Intell Med 45(1):11–34
Tseng P (2001) Convergence of a block coordinate descent method for nondifferentiable minimization. J Optim Theory Appl 109(3):475–494
Weinberger KQ, Blitzer J, Saul LK (2005) Distance metric learning for large margin nearest neighbor classification, In: Advances in neural information processing systems, pp 1473–1480
Ye L, Keogh E (2009) Time series shapelets: a new primitive for data mining, In: Proceedings of the 15th ACM SIGKDD international conference on Knowledge discovery and data mining. ACM, pp 947–956
Yu D, Yu X, Hu Q, Liu J, Wu A (2011) Dynamic time warping constraint learning for large margin nearest neighbor classification. Inf Sci 181:2787–2796
Yuan J-D, Wang Z-H, Han M (2014) A discriminative shapelets transformation for time series classification. Int J Pattern Recognit Artif Intell 28(06):1450014
Yuan J, Wang Z, Han M, Sun Y (2015) A lazy associative classifier for time series. Intell Data Anal 19(5):983–1002
Yuille AL, Rangarajan A (2003) The concave-convex procedure. Neural Comput 15(4):915–936
Zhang H, Ho TB, Zhang Y, Lin M-S (2006) Unsupervised feature extraction for time series clustering using orthogonal wavelet transform. Informatica 30(3)
Acknowledgements
This work is supported by National Natural Science Foundation of China (Nos. 61702030, 61672086, 61771058), Beijing Natural Science Foundation (No. 4182052), and Fundamental Research Funds for the Central Universities (2016RC048).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Yuan, J., Douzal-Chouakria, A., Varasteh Yazdi, S. et al. A large margin time series nearest neighbour classification under locally weighted time warps. Knowl Inf Syst 59, 117–135 (2019). https://doi.org/10.1007/s10115-018-1184-z
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10115-018-1184-z