Fast crawling methods of exploring content distributed over large graphs

Abstract

Despite recent effort to estimate topology characteristics of large graphs (e.g., online social networks and peer-to-peer networks), little attention has been given to develop a formal crawling methodology to characterize the vast amount of content distributed over these networks. Due to the large-scale nature of these networks and a limited query rate imposed by network service providers, exhaustively crawling and enumerating content maintained by each vertex is computationally prohibitive. In this paper, we show how one can obtain content properties by crawling only a small fraction of vertices and collecting their content. We first show that when sampling is naively applied, this can produce a huge bias in content statistics (i.e., average number of content replicas). To remove this bias, one may use maximum likelihood estimation to estimate content characteristics. However, our experimental results show that this straightforward method requires to sample most vertices to obtain accurate estimates. To address this challenge, we propose two efficient estimators: special copy estimator (SCE) and weighted copy estimator (WCE) to estimate content characteristics using available information in sampled content. SCE uses the special content copy indicator to compute the estimate, while WCE derives the estimate based on meta-information in sampled vertices. We conduct experiments on a variety of real-word and synthetic datasets, and the results show that WCE and SCE are cost effective and also “asymptotically unbiased”. Our methodology provides a new tool for researchers to efficiently query content distributed in large-scale networks.

1 Introduction

Nowadays online social networks (OSNs) (e.g., Facebook and Twitter) and content sharing networks (e.g., BitTorrent) are two popular classes of Internet applications. Measuring content characteristics such as file duplication level and information spreading rate on such networks become important since it helps one develop effective advertising strategies [46] and provides valuable information for designing content delivery strategies, e.g., video sharing techniques [28] to increase video pre-fetch accuracy by delivering videos based on users’ social relationships and interests, or to develop information seeding techniques [31] to minimize the peak load of cellular networks by proactively pushing some videos to OSN users. Meanwhile, measuring characteristics of OSNs’ content provided by other networks also helps to understand interactions between different networks. For example, [28] found that 80% of videos in Facebook come from other video service providers such as YouTube.

Due to a limited query (or crawling) rate imposed by network service providers, it is not feasible to collect all content and one must consider using sampling methods to explore content distributed over large networks, because crawling the entire networks is computationally expensive. To solve this problem, one can directly apply sampling methods to content, or it can also collect content from a relatively small fraction of users. Unfortunately, in practice one may not be able to sample content in large networks in a direct manner. For example, for file sharing networks such as BaiduWangPan (in English: Baidu web disk, https://pan.baidu.com) where a node (or user) maintains a list of files, they support users to randomly explore nodes but not files. Similarly, directly sampling tweets on Sina microblog (http://weibo.com) is not feasible. Even when content has a profile webpage, the profile IDs (numeric numbers or strings) of content might be sparsely populated in the ID space, so it is expensive to generate a random yet valid profile ID. Moreover, there may neither have no links between these profile webpages of content. This disables us to directly use crawling methods such as random walks to sample content at random. For example, suppose we want to study statistics of check-in places on Facebook. A check-in place with string name placename has a profile webpage (https://www.facebook.com/placename) on Facebook, and there exist no links between profile webpages of check-in places. In the above scenarios, sampling content requires to first sample a fraction of nodes and then collect their content.

Unfortunately, previous graph sampling work developed for estimating degree or workplace distributions [14, 40] cannot be directly applied in our context. This is because content and vertex are intrinsically different since content may be duplicated. To illustrate this, consider a simple example of a P2P network as shown in Fig. 1. Assume there are two types of files: video and image, each video file such as $F_1$ is cached by a large number of users, each image file such as $F_3$ is cached by a small number of users, and we want to estimate the fraction of distinct video and image files in the P2P network. Clearly, one will overestimate the fraction of video files because video files are more likely to be sampled than image files even when using uniform node sampling. Therefore, methods for estimating topological metrics such as degree distribution cannot be blindly applied. They need to be modified to deal with biases introduced because of the nature of content characterization.

Fig. 1

An example of sampling files in a P2P network

To the best of our knowledge, our work is the first analytical and qualitative study on the problem of estimating characteristics of content distributed over large graphs. We propose methods to accurately estimate content statistics. Our contributions are summarized as:

• We demonstrate that it is challenging to efficiently explore characteristics of content distributed over large graphs, because: (1) when sampling is naively applied, there can be huge bias in computing content statistics; (2) although one can remove this bias using the maximum likelihood estimation, our experimental results show that one needs to sample most vertices in the graph in order to obtain an accurate estimation.

• To solve the above problem, we present two accurate methods to estimate content statistics using available meta-information in sampled content based on two different assumptions, respectively. The first method assumes that we can determine whether a collected content copy is a source or not, which is true for most OSNs that have a label in each content copy to indicate whether it is a source or a duplicated copy. For example, a tweet in microblog networks can be classified as an original tweet or a retweet. Therefore, one can utilize a special content copy set consisting of all original tweets to characterize tweets in the network. To measure statistics of content in these networks, we propose a special copy estimator (SCE) based on collected source content copies. Moreover, we propose another weighted copy estimator (WCE) for networks (e.g., P2P networks) that content (e.g., video) copies have no difference and no meta-data can be used as a special copy indicator. It assumes that each content copy records the number of copies its content holds. This feature is true for many OSNs and P2P networks [52]. Our experimental results show that WCE and SCE are asymptotically unbiased, and WCE is more accurate than SCE, because SCE uses only a fraction of sampled content copies.

• We also use WCE to estimate graph structure statistics for OSNs such as Sina Microblog and Xiami (http://www.xiami.com) where users maintain graph property summaries of their neighbors. For example, by crawling the profile of a user in Sina Microblog, we can obtain its neighbors’ properties such as the number of followers, the number of following, the number of tweets. This allows us to collect more information than previous graph sampling methods under the same sampling cost. Since a user’s graph property summary can be viewed as content maintained by itself and its neighbors, we apply WCE to estimate graph statistics. Our experimental results show that WCE obtains the same accuracy with a much less sampling cost as compared with previous works.

This paper is organized as follows. Section 2 introduces preliminaries. Section 3 presents our crawling methods for estimating characteristics of content in large networks. The performance evaluation and testing results are presented in Sect. 4. Section 5 presents real applications on Sina Microblog Web sites. Related work is given in Sect. 6, and conclusion is given in Sect. 7.

2 Preliminaries

In this section, we briefly review popular graph sampling methods, which are underlying techniques for sampling vertices and content in large networks discussed in Sect. 3. For ease of presentation, we assume the underlying graph is undirected. One way to convert a directed graph into an undirected graph is by ignoring the direction of edges. Consider an undirected graph $G=(V,E)$, where V is the set of vertices and E is the set of undirected edges. Breadth-first search (BFS) is one of most popular graph sampling techniques. However, it introduces a large bias toward high-degree vertices that is unknown and difficult to remove in general graphs [1, 25]. Therefore, we do not consider BFS in this paper. In what follows, we present four popular graph sampling methods: uniform vertex sampling (UNI), random walk (RW), Metropolis–Hastings RW (MHRW) [45], and Frontier sampling (FS) [40]. Unless we state otherwise, we denote ${\varvec{\pi }}=(\pi _v: v\in V)$ as the probability distribution for the underlying sampling method, where $\pi _v$ is defined as the probability of sampling vertex v at each step.

2.1 Sampling method I: uniform vertex sampling

UNI randomly samples vertices from V with replacement. Not all networks support UNI but some do. For example, one can view Wikipedia as a graph and Wikipedia provides a query API to obtain a random vertex (wiki page) sampled from its entire vertices. At each step, UNI samples each vertex v with the same probability, so we have

$$\begin{aligned} \pi _v^{\text {UNI}}=\frac{1}{|V|}, \quad v\in V. \end{aligned}$$

For OSNs such as Facebook, MySpace, Flickr, Renren (http://www.renren.com), Sina Microblog, and Xiami, one can sample users (vertices) as users have numeric IDs. Unfortunately, ID values of users in many networks (e.g., Flickr, Facebook, Sina Microblog, and MySpace) are not sequentially assigned, and the ID space is sparsely populated [39, 41]. Hence, a randomly generated ID may not correspond to a valid user, so considerable computational effort in generating a random ID will be wasted. Therefore, UNI should only be applied to those graphs whose user ID values are densely packed.

2.2 Sampling method II: random walk

RW has been extensively studied in the graph theory literature [30]. From an initial vertex, a walker selects a neighbor at random as the next-hop vertex. The walker moves to this neighbor and repeats the process. Denote $\mathcal {N}(u)$ as the set of neighbors of any vertex u, $\text {deg}(u)=|\mathcal {N}(u)|$ is the degree of u. Formally, RW can be viewed as a Markov chain with transition matrix $P^{\text {RW}}=[P^{\text {RW}}_{u,v}]$, $u,v\in V$, where $P^{\text {RW}}_{u,v}$ is defined as the probability of vertex v being selected as the next-hop vertex given that its current vertex is u, we have:

$$\begin{aligned} P^{\text {RW}}_{u,v}=\left\{ \begin{array}{ll} \frac{1}{\text {deg}(u)} &{}\quad \text {if } v\in \mathcal {N}(u), \\ 0 &{} \quad \text {otherwise.} \end{array} \right. \end{aligned}$$

The stationary distribution ${\varvec{\pi }}^{\text {RW}}$ of this Markov chain is

$$\begin{aligned} \pi _v^{\text {RW}}=\frac{\text {deg}(v)}{2|E|}, \quad v\in V. \end{aligned}$$

For a connected and non-bipartite graph G, the probability of being at a vertex $v\in V$ converges to the above stationary distribution [30]. We can see that ${\varvec{\pi }}^{\text {RW}}$ is biased toward high-degree vertices, but this sampling bias can be removed when we estimate statistics of graph topologies such as node degree distribution [17, 42].

2.3 Sampling method III: Metropolis–Hastings random walk

MHRW [14, 45, 54] provides another way to modify RW using Metropolis–Hastings technique [10, 16, 32], which aims to collect vertices uniformly. To generate a sequence of random samples from a desired stationary distribution $\pi ^{\text {MHRW}}$, the Metropolis–Hastings technique is a Markov chain Monte Carlo method based on modifying the transition matrix of RW as

$$\begin{aligned} P_{u,v}^{\text {MHRW}}=\left\{ \begin{array}{ll} P^{\text {RW}}_{u,v}\min \left( \frac{\pi ^{\text {MHRW}}_v P^{\text {RW}}_{v,u}}{\pi ^{\text {MHRW}}_u P^{\text {RW}}_{u,v}},1\right) &{}\quad \text {if } v\in \mathcal {N}(u),\\ 1-\sum _{w\ne u} P_{u,w}^{MHRW} &{}\quad \text {if }v=u,\\ 0 &{} \quad \text {otherwise}. \end{array} \right. \end{aligned}$$

For a MHRW with target distribution $\pi ^{\text {MHRW}}=\pi ^{\text {UNI}}$, it works as follows: at each step, MHRW selects a neighbor v of current vertex u at random and then accepts the move randomly with probability $\min \left( \frac{\text {deg}(u)}{\text {deg}(v)},1\right)$. Otherwise, MHRW still remains at u. Essentially, MHRW removes the bias of RW at each step by rejecting moves toward high-degree vertices with a certain probability.

2.4 Sampling method IV: Frontier sampling

FS [40] is a centrally coordinated sampling which performs $T\ge 1$ dependent RWs in the graph G of interest. Compared to a single RW, FS is less likely to get stuck in a loosely connected component of G. Denote $\mathbf {L} = (v_1,\ldots , v_T)$ as a vector with T vertices. Each $v_i$ ($1\le i\le T$) is initialized with a random vertex uniformly selected from V. At each step, FS selects a vertex $u\in \mathbf {L}$ with probability $\frac{\text {deg}(u)}{\sum _{\forall v\in \mathbf {L}} \text {deg}(v)}$ and randomly selects a vertex w from $\mathcal {N}(u)$, i.e., the set of neighbors of u. One can easily find that w is uniformly selected from vertices that are connected to the vertices in $\mathbf {L} = (v_1,\ldots , v_T)$. Then, FS replaces u by w in $\mathbf {L}$ and adds w to the sequence of sampled vertices. If G is a connected and non-bipartite graph, the probability of FS sampling a vertex v converges to the following distribution

$$\begin{aligned} \pi _v^{\text {FS}}=\frac{\text {deg}(v)}{2|E|}, \quad v\in V. \end{aligned}$$

2.5 Horvitz–Thompson estimator

Previous work has considered how to estimate topology properties (e.g., degree distribution) via sampling methods. Let $L'(v)$ denote the vertex label of vertex $v\in V$ under study, with range ${\varvec{L'}}=\{l_0',\ldots ,l_{K'}'\}$. Denote vertex label density ${\varvec{\tau }}=(\tau _0,\ldots ,\tau _{K'})$, where $\tau _k$ ($0\le k \le K'$) is the fraction of vertices with label $l_k'$. For example, ${\varvec{\tau }}$ is the degree distribution when $L'(v)$ is defined as the degree of v. To estimate ${\varvec{\tau }}$, RW- and FS-based sampling methods can be viewed as extensions of Horvitz–Thompson estimator [18], which applies inverse probability weighting to account for samples with different probabilities. Therefore, the stationary distribution ${\varvec{\pi }}$ is needed to correct the bias introduced by the underlying sampling method. Since |V| and |E| are usually unknown, unbiasing the error is not straightforward. Instead, one may use a non-normalized stationary distribution $\hat{{\varvec{\pi }}}=(\hat{\pi }_v: v\in V)$ to reweight sampled vertices $s_i$ ($1\le i\le n$), where $\hat{\pi }_v$ is computed as

$$\begin{aligned} \hat{\pi }_v=\left\{ \begin{array}{ll} 1 &{}\quad \text {for UNI and MHRW},\\ \text {deg}(v) &{}\quad \text {for RW and FS}.\\ \end{array} \right. \end{aligned}$$

(1)

Let $\mathbf {1}(\mathbf {P})$ define the indicator function that equals one when predicate $\mathbf {P}$ is true, and zero otherwise. Finally, $\tau _k$ is estimated as

$$\begin{aligned} \hat{\tau }_k=\frac{1}{S}\sum _{i=1}^n \frac{\mathbf {1}(L'(s_i)=l_k')}{\hat{\pi }_{s_i}}, \quad 0\le k \le K', \end{aligned}$$

where $S=\sum _{i=1}^n {\hat{\pi }}_{s_i}^{-1}$.

In summary, RW and FS are biased to sample high-degree vertices. Their biases can be later corrected when we compute topology properties  [14, 38]. Compare the performances of RW and MHRW, and observe that RW is consistently more accurate than MHRW for exploring large networks. Compared to RW and MHRW, Ribeiro and Towsley [40] reveal that FS is more accurate for characterizing loosely connected and disconnect graphs.

3 Content sampling

Our problem To describe our methods formally, we first introduce some notations. For ease of reading, we list notations used throughout the paper in Table 1. Define $L(\mathbf {c})$ as a generic labeling function of content $\mathbf {c}$, with range ${\varvec{L}}=\{l_0,\ldots ,l_K\}$. We focus on developing crawling methods for estimating the content distribution ${\varvec{\omega }}=(\omega _0,\ldots ,\omega _{K})$, where $\omega _k$ ($0\le k \le K$) is the fraction of content with label $l_k$. For example, $L(\mathbf {c})$ can be defined as the number of comments of post $\mathbf {c}$ in OSNs, and then $\omega _k$ is the fraction of posts with k comments, where ${\varvec{L}}=\{0, 1, 2, \ldots \}$. In P2P networks, $L(\mathbf {c})$ can denote the number of replicas of file $\mathbf {c}$; then $\omega _k$ is the fraction of files having k replicas, where ${\varvec{L}}=\{1, 2, \ldots \}$. Similarly $L(\mathbf {c})$ can also be the file type of c in P2P networks, with ${\varvec{L}}=\{l_0=\hbox {``}video\hbox {''}, l_1=\hbox {``}music\hbox {''}, l_2=\hbox {``}text\hbox {''}, l_3=\hbox {``}others\hbox {''}\}$. Then $\omega _k$ ($k=0,1,2,3$) is the fraction of files of type $l_k$. Denote by $\mathbf {C}=\{\mathbf {c}_1, \ldots , \mathbf {c}_H\}$ the set of all content distributed over graph G, where H is the total number of distinct content in G. Then, the content distribution ${\varvec{\omega }}=(\omega _0,\ldots ,\omega _{K})$ is defined as

$$\begin{aligned} \omega _k=\frac{\sum _{\mathbf {c}\in \mathbf {C}} \mathbf {1}(L(\mathbf {c})=l_k)}{H}, \quad k=0,\ldots ,K, \end{aligned}$$

where $L(\mathbf {c})$ is the label of content $\mathbf {c}$ with range $\{l_0,\ldots ,l_K\}$. We assume that n vertices $s_1, \ldots , s_n$ are obtained by a graph sampling method (e.g., UNI, RW, MHRW, or FS) with vertex sampling probability distribution ${\varvec{\pi }}$. Denote by C(v) the set of the content copies maintained by a vertex $v\in V$. Later in Sect. 3.1, we will present two methods DCE and MLE and show that it is difficult to estimate ${\varvec{\omega }}$ solely from sampled content copies $C(s_1), \ldots , C(s_n)$. To solve this challenge, we develop two estimators SCE and WCE utilizing the following two kinds of content meta-information, respectively:

Meta-information 1: special copy indicator We let $c^{*}$ denote a special copy, such as the original source of content $\mathbf {c}$. Note that each content $\mathbf {c}$ has one and only one special copy $c^{*}$. Unless we state otherwise, in what follows the notation $\mathbf {c}$ is used to depict content and c is used to depict a copy of content $\mathbf {c}$. Let $C_{\mathbf {S}}=\{c_1^{*}, \ldots , c_H^{*}\}$ be a special content copy set. For some graphs, sampling methods can check whether a sampled content copy is special or not and generate such a set $C_{\mathbf {S}}$. For example, a tweet in the Sina Microblog can be classified into an original tweet or a retweet; therefore, we can generate $C_{\mathbf {S}}$ consisting of all original tweets.

Meta-information 2: content copy count For content $\mathbf {c} \in \mathbf {C}$, let $f(\mathbf {c})$ denote the number of its copies, and $\{c^{(1)},\ldots ,c^{(f(\mathbf {c}))}\}$ denote the set of its copies appearing in graph G. For networks such as Sina Microblog and Renren, $f(\mathbf {c})$ is available in each content copy $c^{(i)}$, $1\le i\le f(\mathbf {c})$.

Unlike WCE using each and every content copy sampled, SCE only uses a fraction of sampled content copies. Therefore, WCE tends to exhibit smaller estimation errors than SCE. Table 2 summarizes all content sampling methods studied in this paper.

Table 1 A list of notations

Table 2 A comparison of four estimators DCE, MLE, SCE, and WCE

3.1 Challenges

Challenge 1: directly using sampled content copies is biased for characterizing content in large graphs Let $\mathbf {C_D}$ be the set of content that has at least one copy maintained by sampled vertices. One may directly estimate ${\varvec{\omega }}$ using all distinct sampled content $\mathbf {C_D}$ as

$$\begin{aligned} \hat{\omega }_k^{\text {DCE}}=\frac{1}{|\mathbf {C_D}|}\sum _{\mathbf {c}\in \mathbf {C_D}} \mathbf {1}(L(\mathbf {c})=l_k), \quad 0\le k \le K. \end{aligned}$$

We call this straightforward method as Distinct Content Estimator (DCE). For a content copy c, let v(c) be the vertex that maintains c. As alluded, content $\mathbf {c}\in \mathbf {C}$ may be maintained by multiple vertices $v(c^{(j)})$ ($1\le j\le f(\mathbf {c})$) and each vertex $v(c^{(j)})$ is sampled with probability $\pi _{v(c^{(j)})}$, and therefore the probability that one copy of content $\mathbf {c}$ is collected by randomly sampling a vertex is $\sum _{j=0}^{f(\mathbf {c})} \pi _{v(c^{(j)})}$. Note that this probability depends both on the graph sampling method and the number of copies of $\mathbf {c}$; therefore, content in $\mathbf {C_D}$ is not uniformly sampled from $\mathbf {C}$. Even when the UNI sampling method is used, where each vertex u is sampled with the same probability $\pi _u=\frac{1}{|V|}$, the probability that $\mathbf {C_D}$ contains $\mathbf {c}$ is proportional to $f(\mathbf {c})$, i.e., popular content is more likely to be sampled than rare ones. This clearly shows that $\hat{\omega }_k^{\text {DCE}}$ using UNI is still biased.

Challenge 2: it is not easy to correct the sampling bias for characterizing content in large graphs To correct the bias of DCE, we use the maximum likelihood estimation method, which is widely used for inferring statistics of interest from partially observed samples. The details of MLE is given in Appendix. In our experiments, however, we will show that one has to sample a large number of vertices in order to accurately calculate $\hat{\omega }_k^{\text {MLE}}$. It is consistent with results observed in [35].

In summary, it is challenging to characterize content distributed over large networks solely based on regular graph sampling methods. To solve this problem, next, we present two methods utilizing two kinds of meta-information (i.e., an special copy indicator and the number of copies) of content, which are available for each content copy in many OSNs.

3.2 Our unbiased estimator I: special copy estimator (SCE)

SCE estimates ${\varvec{\omega }}$ only using collected special content copies, i.e., content copies in $C_\mathbf {S}$. For content $\mathbf {c}$, $v(c^{*})$ is the vertex maintained its special copy $c^{*}$. Then the probability that $c^{*}$ is collected by sampling a random vertex is $\pi _{v(c^{*})}$. Similar to the Horvitz–Thompson estimator introduced in Sect. 2, we use $\hat{{\varvec{\pi }}}$ defined in Eq. (1) to estimate $\omega _k$ ($0\le k \le K$),

$$\begin{aligned} \hat{\omega }_k^{\text {SCE}}=\frac{1}{S^{\text {SCE}}}\sum _{i=1}^n \sum _{c\in C(s_i)} \frac{\mathbf {1}(L(c)=l_k) \mathbf {1}(c \in C_\mathbf {S})}{\hat{\pi }_{s_i}}, \end{aligned}$$

(2)

where $S^{\text {SCE}}=\sum _{i=1}^n \sum _{c\in C(s_i)} \frac{\mathbf {1}(c \in C_\mathbf {S})}{\hat{\pi }_{s_i}}$. The pseudo-code of SCE is shown in Algorithm 1. The average time complexity of SCE is $O\left( \frac{n\sum _{v\in V} \pi _v |C(v)|}{|V|}\right)$, where $(\pi _v)_{v\in V}$ is the sampling probability distribution of the underlying graph sampling method, which can be any sampling method presented in Sect. 2.

It is important to point out that $\hat{\omega }_k^{\text {SCE}}$ is an asymptotically unbiased estimator of $\omega _k$. For each vertex $v\in V$, Eq. (1) shows that $\pi _v/\hat{\pi }_v$ has the same value, denoted as $S_{\pi }$. We have the following equation for each $k=0,\ldots , K$ and $i=1, \ldots , n$

$$\begin{aligned} \begin{aligned}&\mathbb {E} \left[ \sum _{c\in C(s_i)} \frac{\mathbf {1}(L(c)=l_k) \mathbf {1}(c \in C_\mathbf {S})}{\hat{\pi }_{s_i}}\right] \\&\quad = \sum _{v\in V}\pi _v \sum _{c\in C(v)} \frac{\mathbf {1}(L(c)=l_k) \mathbf {1}(c \in C_\mathbf {S})}{\hat{\pi }_v}\\&\quad = S_{\pi }\sum _{v\in V}\sum _{c\in C(v)}\mathbf {1}(L(c)=l_k) \mathbf {1}(c \in C_\mathbf {S})\\&\quad = S_{\pi }\sum _{c\in C_\mathbf {S}}\mathbf {1}(L(c)=l_k)\\&\quad = S_{\pi } H\omega _k. \end{aligned} \end{aligned}$$

Applying the law of large numbers, we have

$$\begin{aligned} \lim _{n\rightarrow \infty }\frac{1}{n} \sum _{i=1}^n \sum _{c\in C(s_i)} \frac{\mathbf {1}(L(c)=l_k) \mathbf {1}(c \in C_\mathbf {S})}{\hat{\pi }_{s_i}} \,\,\xrightarrow {a.s.} \,\, S_{\pi }H\omega _k, \end{aligned}$$

where “a.s.” denotes “almost sure” converge, i.e., the event happens with probability one. Similarly, we have $\lim _{n\rightarrow \infty } \frac{S^{\text {SCE}}}{n} \xrightarrow {a.s.} S_{\pi }H$. Therefore, $\hat{\omega }_k^{\text {SCE}}$ is an asymptotically unbiased estimator of $\omega _k$.

3.3 Our unbiased estimator II: weighted copy estimator (WCE)

WCE estimates ${\varvec{\omega }}$ using all collected content copies $C(s_i)$ ($1\le i\le n$). This estimator is useful for networks (e.g., Sina Microblog and Renren) in which each copy of any content $\mathbf {c}$ records the value of $f(\mathbf {c})$, the number of copies $\mathbf {c}$ has in the network. Vertex $v(c^{(j)})$ maintains the copy $c^{(j)}$ ($1\le j\le f(\mathbf {c})$) of content $\mathbf {c}$, and it is sampled with probability $\pi _{v(c^{(j)})}$. Meanwhile, a random vertex maintains a copy of $\mathbf {c}$ with probability proportional to $f(\mathbf {c})$. Therefore, we assign a weight $\frac{1}{\hat{\pi }_{v(c^{(j)})} f(\mathbf {c})}$ for $c^{(j)}$ to remove the sampling bias. Finally, we estimate $\omega _k$ ($0\le k \le K$) as

$$\begin{aligned} \hat{\omega }_k^{\text {WCE}}=\frac{1}{S^{\text {WCE}}}\sum _{i=1}^n \sum _{c\in C(s_i)}\frac{\mathbf {1}(L(c)=l_k)}{\hat{\pi }_{s_i} f(c)}, \end{aligned}$$

(3)

where $S^{\text {WCE}}=\sum _{i=1}^n \sum _{c\in C(s_i)}\frac{1}{\hat{\pi }_{s_i} f(c)}$. The pseudo-code of WCE is shown in Algorithm 2. Similar to SCE, the average time complexity of WCE is $O\left( \frac{n\sum _{v\in V} \pi _v |C(v)|}{|V|}\right)$.

$\hat{\omega }_k^{\text {WCE}}$ is an asymptotically unbiased estimator of $\omega _k$. To see that, we have the following equation for each $k=0,\ldots , K$ and $i=1, \ldots , n$

$$\begin{aligned} \begin{aligned}&\text {E}\left[ \sum _{c\in C(s_i)}\frac{\mathbf {1}(L(c)=l_k)}{\hat{\pi }_{s_i} f(c)}\right] \\&\quad =\sum _{v\in V}\pi _v \sum _{c\in C(v)}\frac{\mathbf {1}(L(c)=l_k)}{\hat{\pi }_v f(c)}\\&\quad = S_{\pi }\sum _{v\in V}\sum _{c\in C(v)}\frac{\mathbf {1}(L(c)=l_k)}{f(c)}\\&\quad = S_{\pi }\sum _{\mathbf {c}\in \mathbf {C}} \sum _{j=1}^{f(\mathbf {c})} \frac{\mathbf {1}(L(c^{(j)})=l_k)}{f(c^{(j)})}\\&\quad = S_{\pi }\sum _{\mathbf {c}\in \mathbf {C}} \mathbf {1}(L(\mathbf {c})=l_k)\\&\quad = S_{\pi }H\omega _k. \end{aligned} \end{aligned}$$

Then, we have

$$\begin{aligned} \lim _{n\rightarrow \infty }\frac{1}{n}\sum _{i=1}^n \sum _{c\in C(s_i)}\frac{\mathbf {1}(L(c)=l_k)}{\hat{\pi }_{s_i} f(c)}\xrightarrow {a.s.} S_{\pi }H\omega _k. \end{aligned}$$

Similarly, we have $\lim _{n\rightarrow \infty } \frac{S^{\text {WCE}}}{n} \xrightarrow {a.s.} S_{\pi }H$. Therefore, $\hat{\omega }_k^{\text {WCE}}$ is an asymptotically unbiased estimator of $\omega _k$.

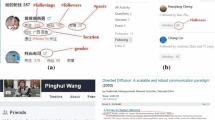
Extend WCE to estimate graph structure statistics We also note that, compared with previous sampling methods [14, 40], WCE is a more cost effective method to estimate graph structure statistics for OSNs (e.g., Sina Microblog and Xiami) which carry such meta-information. As shown in Fig. 2, the webpage of a user in Sina Microblog maintains a summary for each of its neighbors (both followers and following), which includes graph properties such as the number of followers, the number of following, and the number of posts. Hence, one can obtain properties of any vertex vand all its neighbors by simply sampling v. Compared with previous works for measuring structure characteristics, we can obtain more accurate estimates by utilizing the meta-information of sampled vertices. It is important to point that when we use this meta-information, we are biased toward vertices with a large number of neighbors (even when using UNI). Therefore, we need a way to unbias this error. Denote $\text {outdeg}(v)$ as the number of vertices that vertex v follows, and $\text {indeg}(v)$ as the number of vertices that follow v. To remove the sampling bias for observing high-degree vertices’ graph properties, we use WCE to estimate vertex label density ${\varvec{\tau }}=(\tau _0,\ldots ,\tau _{K'})$ defined in Sect. 2, where $\tau _k$ ($0\le k \le K'$) is the fraction of vertices with vertex label $l_k'$. The property summary of each vertex v can be viewed as content with $f'(v)=\text {indeg}(v)+\text {outdeg}(v)+1$ copies maintained by followers, following of v, and v itself. For a collected vertex v, define its associated vertices $C'(v)$ as the collection of its following, followers, and itself. Note that $C'(v)$ might contain duplicated elements because a vertex can be both a following and follower of v. We use WCE to estimate $\tau _k$ ($0\le k \le K'$) as follows

$$\begin{aligned} \hat{\tau }_k^{\text {WCE}}=\frac{1}{S'}\sum _{i=1}^n \sum _{v\in C'(s_i)}\frac{\mathbf {1}(L'(v)=l_k')}{\hat{\pi }_{s_i} f'(v)}, \end{aligned}$$

(4)

where $S'=\sum _{i=1}^n \sum _{v\in C'(s_i)}\frac{1}{\hat{\pi }_{s_i} f'(v)}$. Note that $\hat{\tau }_k^{\text {WCE}}$ is an asymptotically unbiased estimator of $\tau _k$. To see that, we have the following equation for each $k=0,\ldots , K'$ and $i=1, \ldots , n$

$$\begin{aligned} \begin{aligned}&\text {E}\left[ \sum _{v\in C'(s_i)}\frac{\mathbf {1}(L'(v)=l'_k)}{\hat{\pi }_{s_i} f'(v)}\right] \\&\quad =\sum _{u\in V}\pi _u \sum _{v\in C'(u)}\frac{\mathbf {1}(L'(v)=l'_k)}{\hat{\pi }_v f'(v)}\\&\quad = S_{\pi }\sum _{u\in V}\sum _{v\in C'(u)}\frac{\mathbf {1}(L'(v)=l'_k)}{f'(v)}\\&\quad = S_{\pi }\sum _{u\in V} \mathbf {1}(L'(v)=l'_k)\\&\quad = S_{\pi }|V|\tau _k. \end{aligned} \end{aligned}$$

Then, we have

$$\begin{aligned} \lim _{n\rightarrow \infty }\frac{1}{n}\sum _{i=1}^n \sum _{v\in C'(s_i)}\frac{\mathbf {1}(L'(v)=l'_k)}{\hat{\pi }_{s_i} f'(v)}\xrightarrow {a.s.} S_{\pi }|V|\tau _k. \end{aligned}$$

Similarly, we have $\lim _{n\rightarrow \infty } \frac{S'}{n} \xrightarrow {a.s.} S_{\pi }|V|$. Therefore, $\hat{\tau }_k^{\text {WCE}}$ is an asymptotically unbiased estimator of $\tau _k$.

Fig. 2

Graph properties maintained by a vertex v

4 Data evaluation

Our experiments are performed on a variety of real-world networks, which are summarized in Table 3. Xiami is a popular Web site devoted to music streaming and recommendations. Similar to Twitter, Xiami builds a social network based on follower and following relationships. Each user has a numeric ID that is sequentially assigned. We crawled its entire network graph and have made the dataset publicly available (http://www.cse.cuhk.edu.hk/%7ecslui/data). Flickr and YouTube are popular photograph and video sharing Web sites. In these Web sites, a user can subscribe to other user updates such as blogs and photographs. These networks can be represented by a direct graph, with vertices representing users and a directed edge from u to v represents that user u subscribes to user v. Further details of these datasets can be found in [33]. Our experiments are conducted on a Dell Precision T1650 workstation with an Intel Core i7-3770 CPU 3.40 GHz processor and 8 GB DRAM memory.

Table 3 Overview of directed graph datasets used in our simulations

Using real entire graph topologies which are publicly available, we generate benchmark datasets for our simulation experiments by manually generating content and distributing them over these graphs. In the following experiments, we generate $10^7$ distinct content and distribute each content $\mathbf {c}$ using four different content distribution schemes (CDSes): CDS I to CDS IV, which model information distribution mechanisms for undirected and directed graphs. CDSes I and II distribute content with a target content distribution by the number of copies. Define the truncated Pareto distribution as $\phi _k=\frac{\alpha }{\gamma k^{\alpha +1}}$, $k=1,\ldots ,W$, where $\alpha > 0$, $\gamma =\sum _{k=1}^W \frac{\alpha }{k^{\alpha +1}}$, and W is the maximum number of copies. The number of copies for each content $\mathbf {c}$ is randomly selected from set $\{1,\ldots ,W\}$ according to the truncated Pareto distribution with parameter $\alpha$ and W for CDSes I and II. Then, copies of $\mathbf {c}$ are distributed as follows

• CDS I We distribute each content copy to a randomly selected vertex in $G_d$ (one of the directed graph in Table 3).

• CDS II When content has k copies, we first randomly select a vertex v that can reach at least $k-1$ other vertices. Here, two vertices are reachable if there is at least one path between them in the undirected graph G, which is derived from $G_d$ by ignoring the direction of edges. Then, we assign the special (or original) copy of this content to v, and assign $k-1$ duplicated copies to the top $k-1$ nearest vertices in G which are reachable from v.

  CDSes III and IV both distribute each content $\mathbf {c}$ using the independent cascade model [15], that is

• CDS III We distribute $\mathbf {c}$ over the associated undirected graph G. We first distribute the special copy of $\mathbf {c}$ to a randomly selected vertex v. Then we distribute copies of $\mathbf {c}$ to other vertices iteratively. When a new vertex first receives a copy of $\mathbf {c}$, it is given a single chance to distribute a copy of $\mathbf {c}$ to each of its neighbors currently without $\mathbf {c}$ with probability $p_S$.

• CDS IV We distribute $\mathbf {c}$ similar to CDS III but on the direct graph$G_d$. The difference is: when a new vertex first receives a copy of $\mathbf {c}$, it is given a single chance to distribute a copy of $\mathbf {c}$ to each of its incoming neighbors (followers) currently without $\mathbf {c}$ with probability $p_S$.

We would like to point out that $\alpha$ and $p_S$ are parameters for generating our simulation datasets and they are irrelevant to content sampling methods. In the following experiments, we evaluate the performance of our methods for estimating ${\varvec{\omega }}$, the content distribution by the number of copies. Let

$$\begin{aligned} \hbox {NMSE}(\hat{\omega }_j)=\frac{\sqrt{{E}[(\hat{\omega }_j-\omega _j)^2]}}{\omega _j}, \quad j=1,2,\dots , \end{aligned}$$

be a metric that measures the relative error of the estimate $\hat{\omega }_j$ with respect to its true value $\omega _j$. In our experiment, we average the estimates and calculate their NMSE over 1000 runs. Let B denote the sampling budget, which is the number of distinct sampled vertices per run. We set default parameters as: sampling budget $B=0.01|V|$ and the number of random walkers $T=1000$ for FS. To simplify notations, graph sampling method A combined with content estimator B is denoted as method A_B.

Figure 3 shows the average of content distribution estimates of 1000 runs for methods DCE, MLE, SCE, and WCE, where the graph sampling method is UNI, and the content distribution scheme is CDS I with $\alpha =1$ and $W=\{20,50\}$. We observe that DCE is highly biased, while SCE and WCE are unbiased. MLE needs to sample most vertices to reduce biases, especially for large W. Note that SCE and WCE practically coincide with the correct values.

Fig. 3

(Xiami) Average of content distribution estimates for different estimators. a$W = 20$. b$W = 100$

In the following experiments, we set $\alpha =1$ and $W=10^5$ for CDSes I and II, and $p_S=0.01$ for CDSes III and IV. We evaluate the performance of SCE and WCE combined with different graph sampling methods based on the datasets generated by four different CDSes. Figure 4a–d shows the complementary cumulative distribution function (CCDF) of the expectation of content distribution estimates provided by DCE, SCE, and WCE, where the graph is Xiami and the graph sampling method is UNI. We find that DCE exhibits large errors, and SCE and WCE are quite accurate. Similar results are obtained when we use the other four graph sampling methods described in Sect. 2. Figure 4e–t shows the NMSE of SCE and WCE combined with different graph sampling methods for measuring content statistics. The results show that WCE is significantly more accurate than SCE over most points. In particular, WCE is almost an order of magnitude more accurate than SCE for the number of copies larger than 100, and nearly two orders of magnitude more accurate than SCE for the number of copies larger than 1000. Figure 5 shows the compared results for different graph sampling methods where the graph used is Xiami. The results show that UNI is quite accurate and MHRW exhibits large errors for content with a small number of copies. The compared results for WCE show that MHRW is much worse than the other graph sampling methods, while RW and FS have almost the same accuracy. The results for graph YouTube are similar. We show them in Appendix. The time cost of sampling B vertices consists of two parts: (1) computational time and (2) the query response time. In practice, the query response time is usually the bottleneck, because most network service providers impose a query rate limit on crawlers. We can easily find that four graph sampling methods UNI, RW, MHRW, and FS have the similar computational complexity. Moreover, we observe that four estimators DCE, MLE, SCE, and WCE almost exhibit the same computational time. Table 4 shows the computational time for different sampling budget B, where the query response time is not considered. We can see that the computational time increases linearly with B.

Fig. 4

(Xiami) NMSEs of content distribution estimates for different estimators and graph sampling methods. a CDS I. b CDS II. c CDS III. d CDS IV. e UNI, CDS I . f RW, CDS I. g MHRW, CDS I. h FS, CDS I. i UNI, CDS II. j RW, CDS II. k MHRW, CDS II. l FS, CDS II. m UNI, CDS III. n RW, CDS III. o MHRW, CDS III. p FS, CDS III. q UNI, CDS IV. r RW, CDS IV. s MHRW, CDS IV. t FS, CDS IV

Fig. 5

(Xiami) Compared NMSEs of content distribution estimates for WCE using different graph sampling methods. a CDS I. b CDS II. c CDS III. d CDS IV

Table 4 Computational time (seconds) for different sampling budgets and graphs

Figure 6 shows the distributions of users in Xiami using different labels, where the province numbers and corresponding names are shown in Table 5. The fraction of users with more than $10^4$ followers, following, or recommendations is smaller than $2\times 10^{-6}$. The top three popular provinces are Guangdong, Beijing, and Shanghai. Figures 7, 8, 9 and 10 show the results of our methods for estimating vertex label densities. The results show that WCE significantly outperforms previous methods over almost all points. This is because WCE uses neighbors’ graph property summaries of sampled vertices. In particular for UNI_WCE, which is an order of magnitude more accurate than UNI for follower/following counts larger than 100. Figure 11 shows the compared results for different graph sampling methods where the graph used is Xiami. The results show that MHRW is quite accurate. RW and FS almost have the same accuracy. For the follower and recommendation count distributions, UNI is more accurate for follower and recommendation counts with small values. Figures 12 and 13 show the results for estimating out-degree distribution for YouTube and Flickr, respectively. We observe that WCE is better than previous methods over almost all points.

Fig. 6

(Xiami) The distributions of users by different labels. a$\#$ followers, $\#$ following, and $\#$ recommendations. b Location

Table 5 (Xiami) Province numbers and corresponding names

Fig. 7

NMSEs of following count distribution estimates for different graph sampling methods and estimators. a UNI. b RW. c MHRW. d FS

Fig. 8

(Xiami) NMSEs of follower count distribution estimates for different graph sampling methods and estimators. a UNI. b RW. c MHRW. d FS

Fig. 9

(Xiami) NMSEs of recommendation count distribution estimates for different graph sampling methods and estimators. a UNI. b RW. c MHRW. d FS

Fig. 10

(Xiami) NMSEs of location distribution estimates for different graph sampling methods and estimators. a UNI. b RW. c MHRW. d FS

Fig. 11

(Xiami) Compared NMSEs of graph label density estimates for WCE using different graph sampling methods. a$\#$ following. b$\#$ follower. c$\#$ recommendation. d Location

Fig. 12

(YouTube) NMSEs of out-degree distribution estimates for different graph sampling methods and estimators. a UNI. b RW. c MHRW. d FS_WCE versus FS

Fig. 13

(Flickr) NMSEs of out-degree distribution estimates for different graph sampling methods and estimators. a UNI. b RW. c MHRW. d FS

5 Applications

We now apply our methodology to a real OSN, Sina Microblog network, to characterize various content, e.g., the average number of retweets or replies per tweet, types of tweet messages, as well as the associated top rank statistics. By crawling webpages of 148,313 random accounts selected by UNI, we obtain 19.7 million tweets and retweets. Note that in the following analysis, tweets refer to the original tweets. Each tweet or retweet records its original tweet’s information such as the number of retweets and replies. Figure 14 shows the results of estimating the distribution of tweets from retweets and replies using DCE, SCE, and WCE, where the special content is defined as the original tweet for SCE. The estimates for the average number of retweets and replies per tweet are shown in Table 6. We observe that the estimates of SCE and WCE are close to each other, but the estimates obtained by DCE significantly deviate from SCE and WCE. This is consistent with previous experimental results which show that DCE exhibits a large bias. Furthermore, as shown in Fig. 14, we can see that the maximum number of retweets or replies given by SCE is the smallest because it only uses information of sampled original tweets, and the original tweets of popular tweets are not always sampled.

Fig. 14

Distributions of tweets by the number of retweets and replies. a # retweets. b # replies

Table 6 Our estimates of the average number of retweets and replies per tweet

Let us explore the “type” of tweets. We classify tweets into three types: text tweet, image tweet, and video tweet. Table 7 shows their statistics measured by WCE. We find that 60.1% are text tweets, 37.6% are image tweets, and 2.3% are video tweets. On average, image and video tweets have more retweets and replies than text tweets. Table 8 shows the statistics of video tweets by their associated external video source Web sites. We find that the top five popular video Web sites are youku.com (42.7%), tudou.com (26.3%), sina.com (10.0%), yinyuetai.com (6.2%), and 56.com (4.4%).

Table 7 (Sina Microblog) Statistics of tweets by different categories

Table 8 (Sina Microblog) Statistics of video tweets

6 Related work

Little attention has been given to develop a formal crawling methodology to estimate statistics of content over large networks. Zafar et al. [53] conduct an extensive measurement study on comparing the performance of using expert tweets and random sampled tweets on Twitter for applications such as topical search and breaking news detection. Unlike Twitter, in this paper we assume the network of interest does not support an API to sample content at random. Our problem is closely related to research on crawling and sampling large networks. In this paper, we differ crawling and sampling methods as: (1) crawling methods assume that the network of interest is not given in advance, and they aim to accurately estimate network statistics from as few queried nodes as possible because service providers usually impose a rate limit on crawlers; (2) unlike crawling methods, sampling methods assume that the entire network is given in advance, and they aim to design sampling methods to reduce the computational cost of calculating network statistics such as the number of triangles in the network.

Crawling methods for reducing query cost Previous crawling work focuses on designing accurate and efficient methods for measuring graph characteristics, such as vertex degree distribution [14, 38, 40, 41, 45] and the topology of vertices’ groups [24]. Most previous OSN graph crawling and sampling work focuses on undirected graph since each vertex in most OSNs maintains both its incoming and outgoing neighbors, so it is easy to convert these directed OSNs to their associated undirected graphs by ignoring the directions of edges. Breadth-First-Search (BFS) is easy to implement but it introduces a large bias toward high-degree vertices, and it is difficult to remove these biases in general [1, 25, 26]. Random walk (RW) is biased to sample high-degree vertices, however its bias is known and can be corrected [17, 42]. Compared with uniform vertex sampling (UNI), RW has smaller estimation errors for high-degree vertices, and these vertices are quite common for many OSNs like Facebook, Myspace, and Flickr [40]. Furthermore, it is costly to apply UNI in these networks. Metropolis–Hastings RW (MHRW) [14, 45, 54] modifies the RW procedure, and it aims to sample each vertex with the same probability. The accuracy of RW and MHRW is compared in [14, 38]. RW is shown to be consistently more accurate than MHRW. The mixing time of RW determines the efficiency of the sampling, and it is found to be much larger than commonly believed for many OSNs [34]. There are a lot of work on how to decrease the mixing time [3, 7, 11, 13, 23, 40, 55]. Avrachenkov et al. [3] observes that random jumps increase the spectral gap of the random walk, which leads to faster convergence to the steady state distribution. Kurant et al. [23] assigns weights to nodes that are computed using their neighborhood information, and develops a weighted RW-based method to perform stratified sampling on social networks. Dasgupta et al. [11] randomly samples nodes (either uniformly or with a known bias) and then uses neighborhood information to improve its unbiased estimator. Zhou et al. [55] modifies the regular random walk by “rewiring” the network of interest on-the-fly in order to reduce the mixing time of the walk. To sample a directed graph with latent incoming links (e.g., the Web graph and Flickr), Ribeiro et al. [41] use a RW with jumps under the assumption that vertices can be uniformly sampled at random from directed graphs. In addition to node/edge label distribution estimation, Chen et al. and Wang et al. [9, 48] present crawling methods for characterizing graphlets (i.e., small connected subgraph patterns) in large networks.

Sampling methods for reducing computational time Recently, counting triangle in a large graph attracts a lot of attention. Seshadhri et al. and Wu et al.  [43, 51] present sampling algorithms for estimating triangles in a large static graph, which is given in advance and its size can be fitted into memory space.  [2, 4, 8, 19, 20, 37, 44, 47] develop several streaming algorithms for estimating the global count of triangles in a large graph represented as a stream of edges. Jha et al. [19] develop a wedge sampling-based algorithm to estimate the number of triangles in a graph stream. Tsourakakis et et al. [47] present a triangle sparsification method by sampling each and every edge with a fixed probability, which can also be used to estimate triangle counts. Ahmed et al. [2] present a more general edge sampling framework for estimating a variety of graph statistics including the number of triangles. Stefani et al. [44] use a fixed user-specified memory space to sample edges by the reservoir sampling technique. Moreover, [5, 27, 29, 44] develop algorithms for estimating local (i.e., incident to each vertex) counts of triangles in a large graph stream. In addition to triangle counting, a number of algorithms [6, 21, 36, 49, 50] have been developed for estimating high-order graphlet concentrations/counts in a large graph, which is more computationally intensive.

7 Conclusions

In this paper, we study the problem of estimating characteristics of content distributed over large graphs. Our analysis and experimental results show that existing graph sampling methods are biased to sample content with a large number of copies, and there can be a huge bias in statistics computed by using collected content in a direct manner. To remove this bias, the MLE method is applied. However, we observe that MLE needs to sample most vertices in the graph to obtain an accurate estimate. To address this challenge, we develop two accurate methods SCE and WCE using available meta-information in sampled content and prove that they are asymptotically unbiased. We perform extensive experiments and demonstrate that WCE is more accurate than SCE. Furthermore, we use WCE to estimate graph characteristics when vertices maintain their neighbors’ graph properties and conduct experiments to show that WCE is more accurate than regular sampling methods. Our methods SCE and WCE fail to estimate characteristics of content distributed over large graphs when the meta-data of a content do not provide a special copy indicator or the number of copies that the content holds. In future, we plan to solve this limitation.

Appendix

1.1 MLE method

We present the MLE of ${\varvec{\omega }}$ only for graph sampling method UNI, because it is not easy to derive the MLE of ${\varvec{\omega }}$ for other graph sampling methods such as RW, MHRW, and FS. Suppose that the graph size is known (this can be estimated by sampling methods proposed in [22]), $n < |V|$ vertices are sampled and then each copy of $\mathbf {c}$ is sampled with the same probability $p=\frac{n}{|V|}$. For simplicity, we assume that content is distributed over networks uniformly at random. Let M be the maximum number of copies that content has. Denote $P_{i,j}$ as the probability of sampling i copies for content totally having j copies, where $1 \le i \le j \le M$. Let $q=1-p$, we have $P_{i,j}=\frac{\left( {\begin{array}{c}j\\ i\end{array}}\right) p^i q^{j-i}}{1 - q^j}$. We compute the MLE of ${\varvec{\omega }}$ from sampled content copies in respect to the following two cases:

Case 1 When the content label under study is the number of copies associated with content. For randomly sampled content, let $\alpha _i$ ($1\le i\le M$) be the probability that it has i copies sampled. Among sampled content, let $x_i$ be the fraction of content with i copies sampled. We have $\mathbb {E}(x_i) = \alpha _i$. Thus, $x_i$ is an unbiased estimate of $\alpha _i$. Next, we present a method to estimate ${\varvec{\omega }}$ based on the relationship of $\alpha _i$ and ${\varvec{\omega }}$. The likelihood function of $\alpha _i$ is

$$\begin{aligned} \alpha _{i}=\sum _{j=i}^{M} \omega _j P_{i,j}. \end{aligned}$$

(5)

This is similar to packet sampling-based flow size distribution estimation studied in [12], where each packet is sampled with probability p. Here a flow refers to a group of packets with the same source and destination, and the flow size is the number of packets that it contains. In our context, content corresponds to a flow, and its copies correspond to packets in the flow. Therefore, we can develop a maximum likelihood estimate $\hat{\omega }_k^{\text {MLE}}$ of $\omega _k$ ($1\le k\le M$) similar to the method proposed in [12].

Case 2 When the content label under study is independent with the number of duplicates and it is available in each content copy, which is not a latent property such as the number of copies content has, we use the following approach to derive the MLE. Define $\beta _{k,j}$ ($0\le k\le K$, $1\le j\le M$) as the fraction of the number of content with label $l_k$ and j copies over the number of content with label $l_k$. For sampled content, let $\alpha _{k,i}$ ($1\le i\le M$) be the probability that its content label is $l_k$ and has i copies sampled. Then, the likelihood function of $\alpha _{k,i}$ is

$$\begin{aligned} \alpha _{k,i}=\sum _{j=i}^M \beta _{k,j} P_{i,j}. \end{aligned}$$

$\alpha _{k,i}$ can be estimated based on sampled content copies. That is, among sampled content, let $x_{k,i}$ be the fraction of content with label $l_k$ that has i copies sampled. We have $\mathbb {E}(x_{k,i}) = \alpha _{k,i}$. Therefore, $x_{k,i}$ is an unbiased estimate of $\alpha _{k,i}$. Similar to (5), we then develop a maximum likelihood estimate $\hat{\beta }_{k,j}$ of $\beta _{k,j}$, $1\le j\le M$. Since

$$\begin{aligned} \alpha _k=\omega _k \sum _{i=1}^M \sum _{j=i}^M \beta _{k,j} P_{i,j}, \end{aligned}$$

we have the following estimator of $\omega _k$

$$\begin{aligned} \hat{\omega }_k^{\text {MLE}}=\frac{\hat{\alpha }_k}{S^{\text {MLE}}\sum _{i=1}^M \sum _{j=i}^M \hat{\beta }_{k,j} P_{i,j}}, \quad 0\le k\le K, \end{aligned}$$

where $\hat{\alpha }_k$ is the fraction of sampled content with label $l_k$, and

$$\begin{aligned} S^{\text {MLE}}=\sum _{k=0}^K \frac{\hat{\alpha }_k}{\sum _{i=1}^M \sum _{j=i}^M \hat{\beta }_{k,j} P_{i,j}}. \end{aligned}$$