Context-dependent combination of sensor information in Dempster–Shafer theory for BDI

Abstract

There has been much interest in the belief–desire–intention (BDI) agent-based model for developing scalable intelligent systems, e.g. using the AgentSpeak framework. However, reasoning from sensor information in these large-scale systems remains a significant challenge. For example, agents may be faced with information from heterogeneous sources which is uncertain and incomplete, while the sources themselves may be unreliable or conflicting. In order to derive meaningful conclusions, it is important that such information be correctly modelled and combined. In this paper, we choose to model uncertain sensor information in Dempster–Shafer (DS) theory. Unfortunately, as in other uncertainty theories, simple combination strategies in DS theory are often too restrictive (losing valuable information) or too permissive (resulting in ignorance). For this reason, we investigate how a context-dependent strategy originally defined for possibility theory can be adapted to DS theory. In particular, we use the notion of largely partially maximal consistent subsets (LPMCSes) to characterise the context for when to use Dempster’s original rule of combination and for when to resort to an alternative. To guide this process, we identify existing measures of similarity and conflict for finding LPMCSes along with quality of information heuristics to ensure that LPMCSes are formed around high-quality information. We then propose an intelligent sensor model for integrating this information into the AgentSpeak framework which is responsible for applying evidence propagation to construct compatible information, for performing context-dependent combination and for deriving beliefs for revising an agent’s belief base. Finally, we present a power grid scenario inspired by a real-world case study to demonstrate our work.

1 Introduction and related work

Supervisory control and data acquisition (SCADA) systems [5, 10] have been applied in a wide variety of industries including power [1, 26, 27], manufacturing [38] and water treatment [34]. In these settings, SCADA systems deploy large numbers of sensors to collect information for use by control mechanisms, security infrastructure, etc. In the electric power industry, for example, information from sensors may be used to identify faults, preempt outages and manage participation in energy trading markets [39]. However, given this abundance of information from heterogeneous and imperfect sensors, an important challenge is how to accurately model and combine (merge) this information to ensure well-informed decision-making. While this already applies to traditional SCADA systems, it is of particular importance to intelligent and scalable SCADA systems which are gaining increased interest, e.g. those based on autonomous multi-agent frameworks [26, 27]. Therefore, it is also necessary to understand how this information can be used by these more advanced SCADA models.

Within these large systems, sensors represent independent sources of information. For example, in electric power systems, sensors might independently gather information about features of the environment such as voltage, amperage, frequency. However, the information obtained by these sensors may be uncertain or incomplete (e.g. due to noisy measurements) while the sensors themselves may be unreliable (e.g. due to malfunctions, inherent design limitations). Moreover, information from different sensors may be conflicting and so we need some way to combine this information to find a representative and consistent model of the underlying sources. This combined information can then be used for higher-level decision-making. In this paper, we apply the Dempster–Shafer (DS) theory of evidence [31] to model imperfect sensor information since it can be used to model common types of sensor uncertainty (e.g. ignorance and imprecise information) and, more importantly, has mature methods for combining information.

Using DS theory, information from a sensor can be modelled as a mass function. The original and most common method of combining mass functions is using Dempster’s rule of combination [31], which assumes that the mass functions have been obtained from reliable and independent sources. While sensors may be unreliable, there exist methods in DS theory which allow us to first discount unreliable information [31] such that we can then treat this discounted information as fully reliable [25]. Given that our mass functions are independent and can be treated as fully reliable, it would seem that this is a sufficient solution. However, the main problem arises when combining conflicting information. A classical example, introduced by Zadeh [37], illustrates the effect of a high degree of conflict when applying Dempster’s rule. Suppose patient $P_{1}$ is independently examined by two doctors A and B who have the same level of expertise and are equally reliable. A’s diagnosis is that $P_{1}$ has meningitis with probability 0.99 or a brain tumour with probability 0.01. B agrees with A that the probability of a brain tumour is 0.01, but B believes that $P_{1}$ has a concussion with probability 0.99. By applying Dempster’s rule, we would conclude that $P_{1}$ has a brain tumour with probability 1. Clearly, this result is counter-intuitive since it implies complete support for a diagnosis that both A and B considered highly improbable.

Since Zadeh first introduced this counter-example, there has been extensive work on handling conflicts between mass functions. This has resulted in a broad range of approaches which fundamentally differ in how they deal with conflict. We might mention, for example, Smet’s Transferable Belief Model [33] which extends DS theory with an open-world assumption by allowing a nonzero mass to be assigned to the empty set (representing “none of the above”). On the other hand, a popular alternative within standard DS theory—Dubois and Prade’s [13] disjunctive consensus rule being a notable example—is to incorporate all conflict during combination. For example, by applying Dubois and Prade’s rule in Zadeh’s example, we would intuitively conclude that $P_{1}$ has a brain tumour with probability 0.0001. Unfortunately, both approaches tend to increase ignorance when faced with conflict, which is problematic since our goal is to improve support for decision-making. For example, another patient $P_{2}$ is examined by doctors A and B. A’s diagnosis is that $P_{2}$ has meningitis with probability 0.99 or either meningitis, a brain tumour or concussion with probability 0.01. B’s diagnosis is that $P_{2}$ has either meningitis, a brain tumour or concussion with probability 1. By applying Dubois and Prade’s rule, we would only conclude that $P_{2}$ has meningitis, a brain tumour or concussion with probability 1. Clearly, this result is counter-intuitive since it implies complete ignorance about the three possibilities, even though A believes it is highly probable that $P_{2}$ has meningitis. Conversely, by applying Dempster’s rule, we would intuitively conclude that $P_{2}$ has meningitis with probability 0.99.

While there are those who maintain that Dempster’s rule is the only method of combination that should ever be used [16], we argue that no rule is suitable for every situation. In fact, comparable problems have been identified in other uncertainty theories for which adaptive combination strategies have been proposed [12, 14, 15, 17]. In the literature, the majority of the adaptive combination strategies have been proposed in the setting of possibility theory. In general, these approaches focus on deciding when to use a conjunctive rule and when to use a disjunctive rule, where the former is applied to information from reliable and consistent sources aiming to reinforce commonly agreed opinions from multiple sources, while the latter is applied to information from conflicting sources aiming to not dismiss any opinions from any sources. An early proposal was Dubois and Prade’s [12] adaptive combination rule which combines two sources by applying both a conjunctive and disjunctive rule while taking into account the agreement between sources. However, this rule is not associative meaning that it does not reliably extend to combining information from a set of sources. For this reason, there has been more interest in subset-based context-dependent combination strategies. An early example of this approach was proposed in [15] where the combination rule assumes there are n sources from which an unknown subset of j sources are reliable. In this case, a conjunctive rule is applied to all subsets with cardinality j where the cardinality j represents the context for using a conjunctive rule. The conjunctively combined information is then combined using a disjunctive rule. This work was further developed in [14] by proposing a method for deciding on the value of j. Specifically, j was chosen as the cardinality of the largest subset for which the application of a conjunctive rule would result in a normalised possibility distribution. This approach more accurately reflects the specified conditions (i.e. the context) for applying a conjunctive rule in possibility theory than previous adaptive strategies. However, since all the subsets with cardinality j are combined using a conjunctive rule, most of these subsets may contain conflicting information. Thus, the approach does not completely reflect the context for applying a conjunctive rule. Moreover, as highlighted in [17], this approach is not appropriate for dealing with disjoint consistent subsets of different sizes. To address this issue, Hunter and Liu proposed another context-dependent combination strategy in [17] based on finding a partition of sources, rather than a set of fixed-size subsets. They refer to this partition as the set of largely partially maximal consistent subsets (LPMCSes), and again, each LPMCS represents the context for applying a conjunctive rule. However, rather than requiring that each combined LPMCS be a normalised possibility distribution as in [14], they instead define a relaxation of this rule in order to find subsets which are “mostly” in agreement.

With regard to DS theory, sensor fusion is actively used in applications such as robotics [28] and engine diagnostics [2]. Specifically, in Ref. [28], the authors propose an approach to derive mass functions from information obtained from sensor observations and domain knowledge by propagating the evidence into an appropriate frame of features. Once mass functions are derived, they are then combined using a single combination rule, e.g. Dempster’s rule. A robot will then obtain a belief where they can proceed or terminate a task. Alternatively, in Ref. [2], an engine diagnostic problem requires a frame of discernment to represent fault types, mass functions and Dempster’s rule for combination. The authors propose methods of calculating mass functions as well as rational diagnosis decision-making rules and entropy of evidence to improve and evaluate the performance of the combination. They demonstrate through a scenario that decision conflicts can be resolved and the accuracy of fault diagnosis can be improved by combining information from multiple sensors.

Within DS theory, the most relevant work is that proposed by Browne et al. [7]. In this paper, the authors do not actually propose an adaptive combination strategy. Instead, they use the variant of DS theory known as Dezert–Smarandache (DSm) theory to address some of the limitations with standard DS theory in terms of handling conflict and handling non-independent hypotheses. In particular, they propose a notion of maximal consistent subsets which they use to characterise how mass functions should be discounted prior to combination in DSm theory, given a number of possible discounting techniques. Once mass functions have been discounted, they then use the Proportional Conflict Redistribution Rule no. 5 (PCR5) from DSm theory to combine evidence. As far as we are aware, there have been no other approaches to context-dependent combination in DS theory.

To date, the work in [17] is arguably the most accurate reflection of the context for applying a conjunctive rule. For this reason, we propose an approach to combine mass functions based on the context-dependent strategy for combining information in possibility theory. In this way, we aim to characterise the context for when to use Dempster’s rule and for when to resort to an alternative (in this paper we focus on Dubois and Prade’s rule). In particular, when combining a set of mass functions, we first identify a partition of this set using a measure of conflict in DS theory. This accurately reflects the accepted context for Dempster’s rule since, even if a set of mass functions is highly conflicting, it is often possible to find subsets with a low degree of conflict. Likewise, in Ref. [17], the authors use the most appropriate concepts in possibility theory to determine the context for using the combination rule. Each element in this partition is called a LPMCS and identifies a subset which should be combined using Dempster’s rule. Once each LPMCS has been combined using Dempster’s rule, we then resort to Dubois and Prade’s rule to combine the information which is highly conflicting. Moreover, we utilise heuristics on the quality and similarity of mass functions to ensure that each LPMCS is formed around higher-quality information. Similarly, in Ref. [17], the authors use the most appropriate measures in possibility theory for measuring the quality of information. When compared to traditional approaches, our context-dependent strategy allows us to derive more useful information for decision-making while still being able to handle a high degree of conflict between sources.

Turning again to the issue of SCADA systems, we consider a particular multi-agent formulation [35, 36] of SCADA based on the belief–desire–intention (BDI) framework [6]. Recently, there has been interest in using the BDI framework for this purpose due to, among other reasons, its scalability [18]. In this paper, we focus on the AgentSpeak [29] language (for which there are a number of existing implementations [4]) which encodes a BDI agent by a set of predefined plans used to respond to new event-goals. The applicability of these plans is determined by preconditions which are evaluated against the agent’s current beliefs. As such, our new context-dependent combination rule ensures that the agent can reason about a large number of sensors which, in turn, ensures that they are well informed about the current state of the world during plan selection. Importantly, we describe how combined uncertain sensor information can be integrated into this agent model to improve decision-making. In addition, we devise a mechanism to identify when information should be combined which ensures the agent’s beliefs are up-to-date while minimising the computational cost associated with combining information.

In summary, the main contributions of this work are as follows:

• (i) We adapt a context-dependent combination rule from possibility theory to DS theory. In particular, we identify suitable measures from DS theory for determining quality and contextual information used to select subsets for which Dempster’s rule should be applied.

• (ii) We propose to handle uncertain sensor information in the BDI framework using an intelligent sensor. This is responsible for constructing compatible mass functions using evidence propagation, performing context-dependent combination and deriving beliefs for revising an agent’s belief base.

• (iii) Finally, we present a power grid scenario which demonstrates our framework. In particular, we describe the whole process from modelling uncertain sensor information as mass functions to deriving suitable beliefs for an AgentSpeak agent’s belief base along with the effect this has on decision-making.

The remainder of the paper is organised as follows. In Sect. 2, we introduce preliminaries on DS theory. In Sect. 3, we describe our new context-dependent combination rule for mass functions using LPMCSes. In Sect. 4, we demonstrate how to handle uncertain combined sensor information in a BDI agent. In Sect. 5, we present a scenario based on a power grid SCADA system modelled in the BDI framework to illustrate our approach. Finally, in Sect. 6, we draw our conclusions.

2 Preliminaries

DS theory [31] is well suited for dealing with epistemic uncertainty and sensor data fusion.

Definition 1

Let $\varOmega _{}$ be a set of exhaustive and mutually exclusive hypotheses, called a frame of discernment. Then, a function $\mathsf {m}_{}: 2^{\varOmega _{}} \rightarrow [0, 1]$ is called a mass function¹ over $\varOmega _{}$ if $\mathsf {m}_{}(\emptyset ) = 0$ and $\sum _{A \subseteq \varOmega _{}} \mathsf {m}_{}(A) = 1$. Also, a belief function and a plausibility function from $\mathsf {m}_{}$, denoted $\mathsf {Bel}{}$ and $\mathsf {Pl}{}$, are defined for each $A \subseteq \varOmega _{}$ as:

$$\begin{aligned} \mathsf {Bel}{}(A)&= \sum \limits _{B \subseteq A} \mathsf {m}_{}(B), \\ \mathsf {Pl}{}(A)&= \sum \limits _{A \cap B \ne \emptyset } \mathsf {m}_{}(B). \end{aligned}$$

Any $A \subseteq \varOmega _{}$ such that $\mathsf {m}_{}(A) > 0$ is called a focal element of $\mathsf {m}_{}$. Intuitively, $\mathsf {m}_{}(A)$ is the proportion of evidence that supports A, but none of its strict subsets. Similarly, $\mathsf {Bel}{}(A)$ is the degree of evidence that the true hypothesis belongs to A and $\mathsf {Pl}{}(A)$ is the maximum degree of evidence supporting A. The values $\mathsf {Bel}{}(A)$ and $\mathsf {Pl}{}(A)$ represent the lower and upper bounds of belief, respectively. To reflect the reliability of evidence, we can apply a discounting factor to a mass function using Shafer’s discounting technique [31] as follows:

Definition 2

Let $\mathsf {m}_{}$ be a mass function over $\varOmega _{}$ and $\alpha \in [0, 1]$ be a discount factor. Then, a discounted mass function with respect to $\alpha$, denoted $\mathsf {m}_{}^{\alpha }$, is defined for each $A \subseteq \varOmega _{}$ as:

$$\begin{aligned} \mathsf {m}_{}^{\alpha }(A) = \left\{ \begin{array}{l l} (1 - \alpha ) \cdot \mathsf {m}_{}(A), &{} \quad \text{ if }\; A \subset \varOmega _{},\\ \alpha + (1 - \alpha ) \cdot \mathsf {m}_{}(A), &{}\quad \text{ if }\; A = \varOmega _{}. \end{array} \right. \end{aligned}$$

The effect of discounting is to remove mass assigned to focal elements and to then assign this mass to the frame. When $\alpha = 0$, the source is completely reliable, and when $\alpha = 1$, the source is completely unreliable. Once a mass function has been discounted, it is then treated as fully reliable.

Definition 3

Let M be a set of mass functions over $\varOmega _{}$. Then, a function $\mathsf {K}{}: M \times M \rightarrow [0, 1]$ is called a conflict measure and is defined for $\mathsf {m}_{i}, \mathsf {m}_{j} \in M$ as:

$$\begin{aligned} \mathsf {K}{}(\mathsf {m}_{i}, \mathsf {m}_{j}) = \sum _{B \cap C = \emptyset } \mathsf {m}_{i}(B) \mathsf {m}_{j}(C). \end{aligned}$$

Understandably, it has been argued that $\mathsf {K}{}$ is not a good measure of conflict between mass functions [22]. For example, given a mass function $\mathsf {m}_{}$, then it is not necessarily the case that $\mathsf {K}{}(\mathsf {m}_{}, \mathsf {m}_{}) = 0$. Indeed, if $\mathsf {m}_{}$ has any non-nested focal elements, then it will always be the case that $\mathsf {K}{}(\mathsf {m}_{}, \mathsf {m}_{}) > 0$. Conversely, mass functions derived from evidence that is more dissimilar (e.g. by some measure of distance) do not guarantee a higher degree of conflict. However, the reason we consider this measure of conflict rather than more intuitive measures from the literature is that this measure is fundamental to Dempster’s rule [31]:

Definition 4

Let $\mathsf {m}_{i}$ and $\mathsf {m}_{j}$ be mass functions over $\varOmega _{}$ from independent and reliable sources. Then, the combined mass function using Dempster’s rule of combination, denoted $\mathsf {m}_{i} \oplus {} \mathsf {m}_{j}$, is defined for each $A \subseteq \varOmega _{}$ as:

$$\begin{aligned} (\mathsf {m}_{i} \oplus {} \mathsf {m}_{j})(A) = \left\{ \begin{array}{ll} c \sum \limits _{B \cap C = A} \mathsf {m}_{i}(B) \mathsf {m}_{j}(C), &{} \quad \hbox {if}\quad A \ne \emptyset , \\ 0, &{} \quad \hbox {otherwise,} \end{array} \right. \end{aligned}$$

where $c = \frac{1}{1 - \mathsf {K}{}(\mathsf {m}_{i}, \mathsf {m}_{j})}$ is a normalisation constant.

The effect of c is to redistribute the mass value that would otherwise be assigned to the empty set. As mentioned in Sect. 1, Dempster’s rule is only well suited to combine evidence with a low degree of conflict [30]. Importantly, when referring to the “degree of conflict”, we are specifically referring to the $\mathsf {K}{}(\mathsf {m}_{i}, \mathsf {m}_{j})$ value. It is this measure that we will use to determine the context for using Dempster’s rule. In Ref. [13], an alternative to Dempster’s rule was proposed as follows:

Definition 5

Let $\mathsf {m}_{i}$ and $\mathsf {m}_{j}$ be mass functions over $\varOmega _{}$ from independent sources. Then, the combined mass function using Dubois and Prade’s (disjunctive consensus) rule, denoted $\mathsf {m}_{i} \otimes {} \mathsf {m}_{j}$, is defined for each $A \subseteq \varOmega _{}$ as:

$$\begin{aligned} (\mathsf {m}_{i} \otimes {} \mathsf {m}_{j})(A) = \sum _{B \cup C = A} \mathsf {m}_{i}(B) \mathsf {m}_{j}(C). \end{aligned}$$

Dubois and Prade’s rule incorporates all conflict and does not require normalisation. As such, this rule is suitable for combining evidence with a high degree of conflict [30]. Importantly, each combination rule $\odot {} \in \{ \oplus {}, \otimes {} \}$ satisfies the following mathematical properties: $\mathsf {m}_{i} \odot {} \mathsf {m}_{j} = \mathsf {m}_{j} \odot {} \mathsf {m}_{i}$ (commutativity); and $\mathsf {m}_{i} \odot {} (\mathsf {m}_{j} \odot {} \mathsf {m}_{k}) = (\mathsf {m}_{i} \odot {} \mathsf {m}_{j}) \odot {} \mathsf {m}_{k}$ (associativity). This means that combining a set of mass functions using either rule, in any order, will produce the same result. For this reason, given a set of mass functions $M = \{ \mathsf {m}_{1}, \ldots , \mathsf {m}_{n} \}$ over $\varOmega _{}$, we will use:

$$\begin{aligned} \bigodot _{\mathsf {m}_{} \in M} \mathsf {m}_{} \end{aligned}$$

to denote the combined mass function $\mathsf {m}_{1} \odot {} \cdots \odot {} \mathsf {m}_{n}$. It is worth noting, however, that these rules do not satisfy $\mathsf {m}_{} \odot {} \mathsf {m}_{} = \mathsf {m}_{}$ (idempotency).

The ultimate goal in representing and reasoning about uncertain information is to draw meaningful conclusions for decision-making. To translate mass functions to probabilities, a number of existing transformation models can be applied such as those in [9, 11, 32]. One of the most widely used models is Smet’s pignistic model [32] which allows decisions to be made from a mass function on individual hypotheses as follows (note that we use |A| to denote the cardinality of a set A):

Definition 6

Let $\mathsf {m}_{}$ be a mass function over $\varOmega _{}$. Then, a function $\mathsf {BetP}_{\mathsf {m}_{}}: \varOmega _{} \rightarrow [0, 1]$ is called the pignistic probability distribution over $\varOmega _{}$ with respect to $\mathsf {m}_{}$ and is defined for each $\omega _{} \in \varOmega _{}$ as:

$$\begin{aligned} \mathsf {BetP}_{\mathsf {m}_{}}(\omega _{}) = \sum _{A \subseteq \varOmega _{}, \omega _{} \in A} \frac{\mathsf {m}_{}(A)}{|A|}. \end{aligned}$$

3 Context-dependent combination

Various proposals have been suggested in the literature for adaptive combination rules [13, 14, 24]. In this section, we explore ideas presented in [17] for the setting of possibility theory and adapt these to DS theory. In particular, we find suitable measures to replace those used in their work for determining contextual information, including a conflict measure (i.e. the $\mathsf {K}{}$ measure from Dempster’s rule), quality measures (i.e. measures of non-specificity and strife) and a similarity measure (i.e. a distance measure). However, before we explain how to adapt their algorithm to DS theory, we provide the following intuitive summary. First, we identify the highest quality mass function using quality of information heuristics.² This mass function is used as an initial reference point. Second, we find the most similar mass function to this reference. Third, we use Dempster’s rule to combine the reference mass function with the most similar mass function. Fourth, we repeat the second and third steps—using the combined mass function as a new reference point—until the conflict with the next most similar mass function exceeds some specified threshold. The set of mass functions prior to exceeding this threshold constitutes an LPMCS. Finally, we repeat from the first step (on the remaining mass functions) until all mass functions have been added to an LPMCS. Each LPMCS represents a subset of mass functions with similar opinions and a “low” degree of conflict and thus the context for using Dempster’s rule. On the other hand, the set of combined LPMCSes represents highly conflicting information and thus the context for resorting to Dubois and Prade’s rule.

3.1 Preferring high-quality information

The most common methods for characterising the quality of information in DS theory is using measures of non-specificity (related to ambiguity) and strife (i.e. internal conflict). One such measure of non-specificity was introduced in [21] as follows:

Definition 7

Let M be a set of mass functions over $\varOmega _{}$. Then, a function $\mathsf {N}{}: M \rightarrow \mathbb {R}$ is called a non-specificity measure and is defined for each $\mathsf {m}_{} \in M$ as:

$$\begin{aligned} \mathsf {N}{}(\mathsf {m}_{}) = \sum _{A {\subseteq } \varOmega _{} \text { s.t. }A\ne \emptyset } \mathsf {m}_{}(A) \log _{2} |A|. \end{aligned}$$

A mass function $\mathsf {m}_{}$ is completely specific when $\mathsf {N}{}(\mathsf {m}_{}) = 0$ and is completely non-specific when $\mathsf {N}{}(\mathsf {m}_{}) = \log _{2} |\varOmega _{}|$. However, since a frame is a set of mutually exclusive hypotheses, disjoint focal elements imply some disagreement in the information modelled by a mass function. It is this type of disagreement which is characterised by a measure of strife. One such measure was introduced in [21] as follows:

Definition 8

Let M be a set of mass functions over $\varOmega _{}$. Then, a function $\mathsf {S}{}: M \rightarrow \mathbb {R}$ is called a strife measure and is defined for each $\mathsf {m}_{} \in M$ as:

$$\begin{aligned} \mathsf {S}{}(\mathsf {m}_{}) = -\left( \sum _{A \subseteq \varOmega _{} \text { s.t. } A \ne \emptyset } \mathsf {m}_{}(A) \log _{2} \sum _{B \subseteq \varOmega _{} \text { s.t. } B \ne \emptyset } \mathsf {m}_{}(B) \frac{|A \cap B|}{|A|}\right) . \end{aligned}$$

A mass function $\mathsf {m}_{}$ has no internal conflict when $\mathsf {S}{}(\mathsf {m}_{}) = 0$ and has complete internal conflict when $\mathsf {S}{}(\mathsf {m}_{}) = \log _{2} |\varOmega _{}|$. For example, given a mass function $\mathsf {m}_{}$ over $\varOmega _{} = \{ a, b \}$ such that $\mathsf {m}_{}(\{ a \}) = \mathsf {m}_{}(\{ b \}) = 0.5$, then $\mathsf {m}_{}$ has the maximum strife value $\mathsf {S}{}(\mathsf {m}_{}) = 1 = \log _{2} |\varOmega _{}|$. Using these measures for non-specificity and strife allows us to assess the quality of information and, thus, to rank mass functions based on their quality. By adapting Definition 5 from [17], we can define a quality ordering over a set of mass functions as follows:

Definition 9

Let M be a set of mass functions over $\varOmega _{}$. Then, a total order over M, denoted $\succeq _{Q}$, is called a quality order and is defined for $\mathsf {m}_{i}, \mathsf {m}_{j} \in M$ as:

$$\begin{aligned} \mathsf {m}_{i} \succ _{Q} \mathsf {m}_{j}&\Leftrightarrow (\mathsf {N}{}(\mathsf {m}_{i})< \mathsf {N}{}(\mathsf {m}_{j})) \vee (\mathsf {N}{}(\mathsf {m}_{i}) = \mathsf {N}{}(\mathsf {m}_{j}) \wedge \mathsf {S}{}(\mathsf {m}_{i}) < \mathsf {S}{}(\mathsf {m}_{j})), \\ \mathsf {m}_{i} \sim _{Q} \mathsf {m}_{j}&\Leftrightarrow \mathsf {N}{}(\mathsf {m}_{i}) = \mathsf {N}{}(\mathsf {m}_{j}) \wedge \mathsf {S}{}(\mathsf {m}_{i}) = \mathsf {S}{}(\mathsf {m}_{j}). \end{aligned}$$

Moreover, $\mathsf {m}_{i} \succeq _{Q} \mathsf {m}_{j}$ if $\mathsf {m}_{i} \succ _{Q} \mathsf {m}_{j}$ or $\mathsf {m}_{i} \sim _{Q} \mathsf {m}_{j}$. Finally, $\mathsf {m}_{i}$ is said to be of higher quality than $\mathsf {m}_{j}$ if $\mathsf {m}_{i} \succ _{Q} \mathsf {m}_{j}$.

Intuitively, a mass function is of higher quality when it is more specific or when it is equally specific but less internally conflicting. Thus, by definition, a lower non-specificity value is preferred over a lower strife value. Obviously this quality ordering is not a strict order and so does not guarantee a unique highest quality source. We denote the set of highest quality mass functions in M as ${\max (M, \succeq _{Q})} = \{ \mathsf {m}_{} \in M \mid \not \exists \mathsf {m}_{}' \in M, \mathsf {m}_{}' \succ _{Q} \mathsf {m}_{} \}$. To handle the situation where there are multiple highest quality mass functions, we make the assumption of a prior strict preference ordering over sources, denoted $\succ _{P}$. Given a set of mass functions M over $\varOmega _{}$, then for all $\mathsf {m}_{i}, \mathsf {m}_{j} \in M$ we say that $\mathsf {m}_{i}$ is more preferred than $\mathsf {m}_{j}$ if $\mathsf {m}_{i} \succ _{P} \mathsf {m}_{j}$. This preference ordering may be based on the reliability of sources, the significance of sources, the order in which sources have been queried, etc. We denote the (unique) most preferred mass function in M as $\max (M, \succ _{P}) = \mathsf {m}_{}$ such that $\mathsf {m}_{} \in M$ and $\not \exists \mathsf {m}_{}' \in M, \mathsf {m}_{}' \succ _{P} \mathsf {m}_{}$.

Definition 10

Let M be a set of mass functions over $\varOmega _{}$. Then, the mass function $\mathsf {Ref}{}(M) = \max (\max (M, \succeq _{Q}), \succ _{P})$ is called the reference mass function in M.

Table 1 Non-specificity and strife values for a set of mass functions $M = \{ \mathsf {m}_{1}, \mathsf {m}_{2}, \mathsf {m}_{3} \}$ over $\varOmega _{} = \{ a, b, c \}$

Example 1

Given the set of mass functions M as well as the non-specificity and strife values for M as shown in Table 1, then the quality ordering over M is $\mathsf {m}_{1} \succ _{Q} \mathsf {m}_{2} \succ _{Q} \mathsf {m}_{3}$. Thus, regardless of the preference ordering over M, the reference mass function in M is $\mathsf {Ref}{}(M) = \mathsf {m}_{1}$.

A reference mass function is a mass function with the maximum quality of information. When this is not unique, we select the most preferred mass function from the set of mass functions with the maximum quality of information. As we will see in Sect. 3.2, a reference mass function is a mass function around which an LPMCS is formed. Thus, defining a reference mass function in this way allows us to prefer higher-quality information when finding LPMCSes.

3.2 Defining the context for combination rules

While our motivation in finding a reference mass function is to prefer higher-quality information, it is possible that high-quality mass functions are also highly conflicting. As such, it is not advisable to rely on the quality ordering for choosing the next mass function to consider since this may result in smaller LPMCSes than is necessary. On the other hand, as mentioned in Sect. 2, the conflict measure $\mathsf {K}{}$ may assign a low degree of conflict to very dissimilar information. Therefore, relying on the conflict measure for choosing the next mass function to consider does not reflect our stated aim of forming LPMCSes around higher-quality information. For this reason, we resort to a distance measure since this is a more appropriate measure of similarity. In DS theory, distance measures have been studied extensively in the literature and have seen theoretical and empirical validation [20]. One of the most popular distance measures was proposed by Jousselme et al. [19] as follows:

Definition 11

Let M be a set of mass functions over $\varOmega _{}$. Then, a function $\mathsf {d}{}: M \times M \rightarrow \mathbb {R}$ is called a distance measure and is defined for $\mathsf {m}_{i}, \mathsf {m}_{j} \in M$ as:

$$\begin{aligned} \mathsf {d}{}(\mathsf {m}_{i}, \mathsf {m}_{j}) = \sqrt{\frac{1}{2} \left( \overrightarrow{\mathsf {m}_{i}} - \overrightarrow{\mathsf {m}_{j}}\right) ^{T} D\left( \overrightarrow{\mathsf {m}_{i}} - \overrightarrow{\mathsf {m}_{j}}\right) }, \end{aligned}$$

where $\overrightarrow{\mathsf {m}_{}}$ is a vector representation of mass function $\mathsf {m}_{}$, $\overrightarrow{\mathsf {m}_{}}^T$ is the transpose of vector $\overrightarrow{\mathsf {m}_{}}$, and D is a $2^{\varOmega _{}} \times 2^{\varOmega _{}}$ similarity matrix whose elements are $D(A, B) = \frac{|A \cap B|}{|A \cup B|}$ such that $A, B \subseteq \varOmega _{}$.

Importantly, for any mass functions $\mathsf {m}_{}$, we have that $\mathsf {d}{}(\mathsf {m}_{}, \mathsf {m}_{}) = 0$. We can formalise the semantics of this distance measure over a set of mass functions as follows:

Definition 12

Let M be a set of mass functions over $\varOmega _{}$ and $\mathsf {m}_{}$ be a mass function over $\varOmega _{}$. Then, a total order over M, denoted $\preceq ^{\mathsf {m}_{}}_{\mathsf {d}{}}$, is called a distance order with respect to $\mathsf {m}_{}$ and is defined for $\mathsf {m}_{i}, \mathsf {m}_{j} \in M$ as:

$$\begin{aligned} \mathsf {m}_{i} \preceq ^{\mathsf {m}_{}}_{\mathsf {d}{}} \mathsf {m}_{j} \Leftrightarrow \mathsf {d}{}(\mathsf {m}_{}, \mathsf {m}_{i}) \le \mathsf {d}{}(\mathsf {m}_{}, \mathsf {m}_{j}). \end{aligned}$$

Moreover, $\mathsf {m}_{i} \sim ^{\mathsf {m}_{}}_{\mathsf {d}{}} \mathsf {m}_{j}$ if $\mathsf {m}_{i} \preceq ^{\mathsf {m}_{}}_{\mathsf {d}{}} \mathsf {m}_{j}$ and $\mathsf {m}_{j} \preceq ^{\mathsf {m}_{}}_{\mathsf {d}{}} \mathsf {m}_{i}$. Also, $\mathsf {m}_{i} \prec ^{\mathsf {m}_{}}_{\mathsf {d}{}} \mathsf {m}_{j}$ if $\mathsf {m}_{i} \preceq ^{\mathsf {m}_{}}_{\mathsf {d}{}} \mathsf {m}_{j}$ and $\mathsf {m}_{j} \npreceq ^{\mathsf {m}_{}}_{\mathsf {d}{}} \mathsf {m}_{i}$. We say that $\mathsf {m}_{i}$ is closer to $\mathsf {m}_{}$ than $\mathsf {m}_{j}$ is to $\mathsf {m}_{}$ if $\mathsf {m}_{i} \prec ^{\mathsf {m}_{}}_{\mathsf {d}{}} \mathsf {m}_{j}$.

We denote the set of closest mass functions in M to $\mathsf {m}_{}$ as ${\min (M, \preceq ^{\mathsf {m}_{}}_{\mathsf {d}{}})} = \{ \mathsf {m}_{}' \in M \mid \not \exists \mathsf {m}_{}'' \in M, \mathsf {m}_{}'' \prec ^{\mathsf {m}_{}}_{\mathsf {d}{}} \mathsf {m}_{}' \}$. Using this distance ordering and the previously defined reference mass function, we can then define a preferred sequence for combining a set of mass functions with Dempster’s rule by adapting Definition 9 from [17] as follows:

Definition 13

Let $M = \{ \mathsf {m}_{1}, \ldots , \mathsf {m}_{n} \}$ be a set of mass functions over $\varOmega _{}$ such that $n \ge 1$. Then, the sequence $(\mathsf {m}_{1}, \ldots , \mathsf {m}_{n})$ is called the preferred sequence for combining M if one of the following conditions is satisfied: (i) $n = 1$; or (ii) $n > 1$, $\mathsf {Ref}{}(M) = \mathsf {m}_{1}$ and for each $i \in 2, \ldots , n$, we have that:

$$\begin{aligned} \mathsf {m}_{i} = \max \left( \min \left( \{ \mathsf {m}_{i}, \ldots , \mathsf {m}_{n} \}, \preceq ^{\mathsf {m}_{1} \oplus {} \ldots \oplus {} \mathsf {m}_{i-1}}_{\mathsf {d}{}}\right) , \succ _{P}\right) . \end{aligned}$$

Table 2 Distance and conflict values for the set of mass functions M from Table 1

Example 2

(Continuing Example 1) Given the distance values for M as shown in Table 2, then the preferred sequence for combining M is ($\mathsf {m}_{1}, \mathsf {m}_{2}, \mathsf {m}_{3}$).

Again we resort to the prior preference ordering over mass functions if there does not exist a unique mass function which is closest to the previously combined mass functions. From this preferred sequence of combination, we can then identify an LPMCS directly. Specifically, given a set of mass functions, then an LPMCS is formed by applying Dempster’s rule to the first m elements in the sequence until the conflict between the combined m mass functions and the next mass function exceeds a specified threshold. This threshold reflects the degree of conflict which we are willing to tolerate and is thus domain specific. By adapting Definition 10 from [17], we have the following:

Definition 14

Let M be a set of mass functions over $\varOmega _{}$, $(\mathsf {m}_{1}, \ldots , \mathsf {m}_{n})$ be the preferred sequence for combining M such that $n = |M|$ and $n \ge 1$ and $\epsilon _{\mathsf {K}{}}$ be a conflict threshold. Then, a set of mass functions $\{ \mathsf {m}_{1}, \ldots , \mathsf {m}_{m} \} \subseteq M$ such that $1 \le m \le n$ is called the largely partially maximal consistent subset (LPMCS) with respect to $\epsilon _{\mathsf {K}{}}$, denoted $\mathsf {L}(M, \epsilon _{\mathsf {K}{}})$, if one of the following conditions is satisfied:

• (i) $n = 1$;

• (ii) $m = 1$, $n > 1$ and $\mathsf {K}{}(\mathsf {m}_{1} \oplus {} \ldots \oplus {} \mathsf {m}_{m}, \mathsf {m}_{m+1}) > \epsilon _{\mathsf {K}{}}$;

• (iii) $m > 1$, $m = n$ and for each $i \in 2, \ldots , m$ then $\mathsf {K}{}(\mathsf {m}_{1} \oplus {} \ldots \oplus {} \mathsf {m}_{i-1}, \mathsf {m}_{i}) \le \epsilon _{\mathsf {K}{}}$;

• (iv) $m > 1$, $m < n$ and for each $i \in 2, \ldots , m$ then $\mathsf {K}{}(\mathsf {m}_{1} \oplus {} \ldots \oplus {} \mathsf {m}_{i-1}, \mathsf {m}_{i}) \le \epsilon _{\mathsf {K}{}}$ but $\mathsf {K}{}(\mathsf {m}_{1} \oplus {} \ldots \oplus {} \mathsf {m}_{m}, \mathsf {m}_{m+1}) > \epsilon _{\mathsf {K}{}}$.

Example 3

(Continuing Example 2) Given the conflict values for M as shown in Table 2 and a conflict threshold $\epsilon _{\mathsf {K}{}} = 0.4$, then the LPMCS in M is $\mathsf {L}(M, 0.4) = \{ \mathsf {m}_{1}, \mathsf {m}_{2} \}$ since $\mathsf {K}{}(\mathsf {m}_{1}, \mathsf {m}_{2}) = 0.36 \le 0.4$ but $\mathsf {K}{}(\mathsf {m}_{1} \oplus {} \mathsf {m}_{2}, \mathsf {m}_{3}) = 0.457 > 0.4$.

In this way, an LPMCS is the set of mass functions corresponding to the first maximal subsequence (from the preferred sequence of combination) where the conflict is deemed (by the conflict threshold) to be sufficiently low enough to apply Dempster’s rule. The complete set of LPMCSes can then be recursively defined as follows:

Definition 15

Let M be a set of mass functions over $\varOmega _{}$, $\epsilon _{\mathsf {K}{}}$ be a conflict threshold and $\mathsf {L}(M,\epsilon _{\mathsf {K}{}}) \subseteq M$ be the LPMCS in M. Then, the set of LPMCSes in M, denoted $\mathsf {L^{*}}(M, \epsilon _{\mathsf {K}{}})$, is a partition of M defined as:

$$\begin{aligned} \mathsf {L^{*}}(M, \epsilon _{\mathsf {K}{}}) = \left\{ \begin{array}{l l} \{ \mathsf {L}(M, \epsilon _{\mathsf {K}{}}) \} &{} \quad \hbox {if} \quad M {\setminus } \mathsf {L}(M, \epsilon _{\mathsf {K}{}}) \ne \emptyset ; \\ \quad \cup \mathsf {L^{*}}(M {\setminus } \mathsf {L}(M, \epsilon _{\mathsf {K}{}}), \epsilon _{\mathsf {K}{}}), &{} \\ \{ \mathsf {L}(M, \epsilon _{\mathsf {K}{}}) \}, &{}\quad \hbox {otherwise.} \end{array} \right. \end{aligned}$$

Example 4

(Continuing Example 3) Given that $\mathsf {L}(M,\epsilon _{\mathsf {K}{}}) = \{ \mathsf {m}_{1}, \mathsf {m}_{2} \}$, then by the first condition in Definition 15 we have that $\mathsf {L^{*}}(M, \epsilon _{\mathsf {K}{}}) = \{\{\mathsf {m}_{1}, \mathsf {m}_{2}\}\} \cup \mathsf {L^{*}}(\{\mathsf {m}_{3}\}, \epsilon _{\mathsf {K}{}})$, since $M \backslash \{m1, m2\} = \{m3\} \ne \emptyset$. Now, by condition (i) in Definition 14, we have that $\mathsf {L}(\{\mathsf {m}_{3}\}, \epsilon _{\mathsf {K}{}}) = \{\mathsf {m}_{3}\}$. Thus $\mathsf {L^{*}}(\{\mathsf {m}_{3}\}, \epsilon _{\mathsf {K}{}}) = \{\{\mathsf {m}_{3}\}\}$ by the second condition in Definition 15 since $\{\mathsf {m}_{3}\} \backslash \{\mathsf {m}_{3}\} = \emptyset$. Therefore, the set of LPMCSes in M is $\mathsf {L^{*}}(M, \epsilon _{\mathsf {K}{}}) = \{\{\mathsf {m}_{1}, \mathsf {m}_{2}\}\} \cup \{\{\mathsf {m}_{3}\}\} = \{\{\mathsf {m}_{1}, \mathsf {m}_{2}\}, \{\mathsf {m}_{3}\}\}$.

Having defined the set of LPMCSes, we can now define our context-dependent combination rule using both Dempster’s rule and Dubois and Prade’s rule as follows:

Definition 16

Let M be a set of mass functions from independent and reliable sources and $\epsilon _{\mathsf {K}{}}$ be a conflict threshold. Then, the combined mass function from M with respect to $\epsilon _{\mathsf {K}{}}$ using the context-dependent combination rule is defined as:

$$\begin{aligned} \bigotimes _{M' \in \mathsf {L^{*}}(M, \epsilon _{\mathsf {K}{}})} \bigoplus _{\mathsf {m}_{} \in M'} \mathsf {m}_{}. \end{aligned}$$

In other words, the combined mass function is found by combining each LPMCS using Dempster’s rule and then combining the set of combined LPMCSes using Dubois and Prade’s rule.

Table 3 Combined mass functions from the set of mass functions M from Table 1

Example 5

(Continuing Example 4) Given a conflict threshold $\epsilon _{\mathsf {K}{}} = 0.4$, then the context-dependent combined mass function from M with respect to $\epsilon _{\mathsf {K}{}}$ is shown in Table 3. For comparison, the combined mass functions using only Dempster’s rule and only Dubois and Prade’s rule are also shown in Table 3.

It is evident from Example 5 that the context-dependent combination rule finds a balance between the two other combination rules: neither throwing away too much information (as is the case with Dempster’s rule), nor incorporating too much conflict such that it is difficult to make decisions (as is the case with Dubois and Prade’s rule).

3.3 Computational aspects

Algorithm 1 provides a method for executing context-dependent combination of a set of mass functions M, given a conflict threshold $\epsilon _{\mathsf {K}{}}$ and strict preference ordering $\succ _{P}$. On line 1, the set of LPMCSes is initialised. On line 2, a list of mass functions representing the combined quality and preference orderings can be constructed with respect to the non-specificity and strife values of each mass function in M and the preference ordering $\succ _{P}$. The first element in this list would then be selected as the initial reference mass function $\mathsf {m}_{r}$ as in Definition 10. Moreover, this list can be referred to again on line 11. Lines 5–8 describe how to compute an LPMCS with respect to the current reference mass function $\mathsf {m}_{r}$. Specifically, on line 5, $\mathsf {m}_{c}$ represents the closest and most preferred mass function to $\mathsf {m}_{r}$ as in Definition 13. It is not necessary to compute the full ordering $\succeq ^{\mathsf {m}_{r}}_{\mathsf {d}{}}$ on line 5; instead, we only require one iteration through M (in order of $\succ _{P}$) to find $\mathsf {m}_{c}$. This mass function is compared with $\mathsf {m}_{r}$ on line 6 which represents the condition for including a mass function in the current LPMCS as in Definition 14. On line 7, we combine the reference mass function with the closest and most preferred mass function, and this combined mass function becomes our new reference. Lines 9–12 describe the behaviour when a complete LPMCS has been found. In particular, the complete LPMCS (which has been combined using Dempster’s rule) is added to the set of previously found LPMCSes on line 10. Then, on line 11, we find the reference mass function for a new LPMCS by referring back to the combined quality and preference list constructed on line 2. Finally, when there are no remaining mass functions in M, the current reference $\mathsf {m}_{r}$ represents the final combined LPMCS. However, this LPMCS is not added to the set of LPMCSes $M'$, rather we just begin combining each combined LPMCS in $M'$ with $\mathsf {m}_{r}$ using Dubois and Prade’s rule as described on lines 13 and 14. Once this is complete, the mass function $\mathsf {m}_{r}$ represents the final context-dependent combined mass function as in Definition 16 and this is returned on line 15.

Proposition 1

The complexity of applying the context-dependent combination rule on a set of mass functions M is $\mathcal {O}{}(n^{2})$ such that $n = |M|$.

Proof

In order to select a reference mass function, we only need to compute n pairs of non-specificity and strife values. Thus, the complexity of selecting a reference mass function is $\mathcal {O}{}(n)$. After selecting a reference mass function, there can be at most $n - 1$ mass functions which have not been added to an LPMCS. In this case, selecting a closest and most preferred mass function requires the computation of $n - 1$ distance values. Thus, the complexity of selecting a closest and most preferred mass function is also $\mathcal {O}{}(n)$. In the worst case, where every LPMCS is a singleton, we need to select n reference mass functions of which there are $n - 1$ requiring the selection of a closest and most preferred mass function. Thus, the overall complexity is $\mathcal {O}{}(n^{2})$.

4 Handling sensor information in BDI

In this section we begin by introducing preliminaries on the AgentSpeak framework [29] for BDI agents. We then describe the necessary steps for handling uncertain sensor information in AgentSpeak. In Sect. 5, we will present a power grid SCADA scenario which demonstrates how sensor information can be modelled and combined using DS theory and then incorporated into a BDI agent defined in AgentSpeak.

4.1 AgentSpeak

AgentSpeak is a logic-based programming language related to a restricted form of first-order logic, combined with notions for events and actions. In practice, it shares many similarities with popular logic programming languages such as Prolog. The language itself consists of variables, constants, predicate symbols, action symbols, logical connectives and punctuation. Following logic programming convention, variables begin with uppercase letters, while constants, predicate symbols and action symbols begin with lowercase letters. As in first-order logic, these constructs can be understood as terms, i.e. a variable is a term, a constant is a term, and if p is an n-ary predicate symbol and $t_{1}, \ldots , t_{n}$ are terms, then $p(t_{1}, \ldots , t_{n})$ is a term. A term is said to be ground or instantiated if there are no variables or if each variable is bound to a constant by a unifier. We will use $\mathbf t$ to denote the terms $t_{1}, \ldots , t_{n}$. The supported logical connectives are $\lnot$ and $\wedge$ for negation and conjunction, respectively. Also, the punctuation in AgentSpeak includes !, ?, ;  and $\leftarrow$ and the meaning of each will be explained later. From [29], the syntax of the AgentSpeak language is defined as follows:

Definition 17

If b is a predicate symbol, then $b(\mathbf t )$ is a belief atom. If $b(\mathbf t )$ is a belief atom, then $b(\mathbf t )$ and $\lnot b(\mathbf t )$ are belief literals.

Definition 18

If g is a predicate symbol, then $!g(\mathbf t )$ and $?g(\mathbf t )$ are goals where $!g(\mathbf t )$ is an achievement goal and $?g(\mathbf t )$ is a test goal.

Definition 19

If $b(\mathbf t )$ is a belief atom and $!g(\mathbf t )$ and $?g(\mathbf t )$ are goals, then $+b(\mathbf t )$, $-b(\mathbf t )$, $+!g(\mathbf t )$, $-!g(\mathbf t )$, $+?g(\mathbf t )$ and $-?g(\mathbf t )$ are triggering events where $+$ and − denote addition and deletion events, respectively.

Definition 20

If a is an action symbol, then $a(\mathbf t )$ is an action.

Definition 21

If e is a triggering event, $l_{1}, \ldots , l_{m}$ are belief literals and $h_{1}, \ldots , h_{n}$ are goals or actions, then $e: l_{1} \wedge \ldots \wedge l_{m} \leftarrow h_{1}; \ldots ; h_{n}$ is a plan where $l_{1} \wedge \ldots \wedge l_{m}$ is the context and $h_{1}; \ldots ; h_{n}$ is the body such that ;  denotes sequencing.

An AgentSpeak agent $\mathbb {A}$ is a tuple $\langle Bb, Pl, A, E, I \rangle$ ³ with a belief base Bb, a plan library Pl, an action set A, an event set E and an intention set I. The belief base Bb is a set of belief atoms⁴ which describe the agent’s current beliefs about the world. The plan library Pl is a set of predefined plans used for reacting to new events. The action set A contains the set of primitive actions available to the agent. The event set E contains the set of events which the agent has yet to consider. Finally, the intention set I contains those plans which the agent has chosen to pursue where each intention is a stack of partially executed plans. Intuitively, when an agent reacts to a new event e, it selects those plans from the plan library which have e as their triggering event (called the relevant plans for e). A relevant plan is said to be applicable when the context of the plan evaluates to true with respect to the agent’s current belief base. For a given event e, there may be many applicable plans from which one is selected and either added to an existing intention or used to form a new intention. Intentions in the intention set are executed concurrently. Each intention is executed by performing the steps described in the body of each plan in the stack (e.g. executing primitive actions or generating new subgoals). Thus, the execution of an intention may change the environment and/or the agent’s beliefs. As such, if the execution of an intention results in the generation of new events (e.g. the addition of subgoals), then more plans may be added to the stack for execution. In Sect. 5, we will consider AgentSpeak programs in more detail, but for the rest of this section, we are primarily interested in how to derive belief atoms from sensors.

4.2 Deriving beliefs from uncertain sensor information

By their nature, heterogeneous sensors output different types of sensor information. While this presents some important practical challenges in terms of how to construct mass functions from original sensor information, any solutions will be unavoidably domain-specific. In this paper, we do not attempt to address this issue directly, but we can suggest some possibilities. For example, if a sensor returns numerical information in the form of an interval, then we can assign a mass of 1 to the set of discrete readings included in the interval. Similarly, if a sensor returns a reading with a certainty of 80 %, then we can assign a mass of 0.8 to the relevant focal set. So, without loss of generality, we assume that an appropriate mass function can be derived from any source. Moreover, we assume that each source has a reliability degree $1 - \alpha$ and that each mass function has been discounted with respect to the $\alpha$ value of the originating source. Thus, for the remainder of this section, we assume that each mass function is actually a discounted mass function $\mathsf {m}_{}^{\alpha }$ which can be treated as fully reliable. However, it is unlikely that all compatible sources (i.e. sources with information which is suitable for combination) will return strictly compatible mass functions (i.e. mass functions defined over the same frame). To address this issue, the notion of an evidential mapping was introduced in [23] as follows:

Definition 22

Let $\varOmega _{e}$ and $\varOmega _{h}$ be frames. Then, a function $\varGamma {}: \varOmega _{e} \times 2^{\varOmega _{h}} \rightarrow [0, 1]$ is called an evidential mapping from $\varOmega _{e}$ to $\varOmega _{h}$ if for each $\omega _{e} \in \varOmega _{e}$, $\varGamma {}(\omega _{e}, \emptyset ) = 0$ and $\sum _{H \subseteq \varOmega _{h}} \varGamma {}(\omega _{e}, H) = 1$.

In other words, for each $\omega _{e} \in \varOmega _{e}$, an evidential mapping defines a mass function over $\varOmega _{h}$ which describes how $\omega _{e}$ relates to $\varOmega _{h}$. In line with DS terminology, a set $H \subseteq \varOmega _{h}$ is called a projected focal element of $\omega _{e} \in \varOmega _{e}$ if $\varGamma {}(\omega _{e}, H) > 0$. Importantly, given a mass function over $\varOmega _{e}$, then an evidential mapping allows us to derive a new mass function over $\varOmega _{h}$ directly as follows [23]:

Definition 23

Let $\varOmega _{e}$ and $\varOmega _{h}$ be frames, $\mathsf {m}_{e}$ be a mass function over $\varOmega _{e}$ and $\varGamma {}$ be an evidential mapping from $\varOmega _{e}$ to $\varOmega _{h}$. Then, a mass function $\mathsf {m}_{h}$ over $\varOmega _{h}$ is called an evidence propagated mass function from $\mathsf {m}_{e}$ with respect to $\varGamma {}$ and is defined for each $H \subseteq \varOmega _{h}$ as:

$$\begin{aligned} \mathsf {m}_{h}(H) = \sum _{E \subseteq \varOmega _{e}} \mathsf {m}_{e}(E) \varGamma {}^{*}{}(E, H), \end{aligned}$$

where:

$$\begin{aligned} \varGamma {}^{*}{}(E, H) = \left\{ \begin{array}{ll} \sum _{\omega _{e} \in E} \frac{\varGamma {}(\omega _{e}, H)}{|E|}, &{}\quad \hbox {if}\quad H \ne \bigcup H_{E} \wedge \forall \omega _{e} \in E, \varGamma {}(\omega _{e}, H)>0, \\ 1 - \sum _{H' \in H_{E}} \varGamma {}^{*}{}(E, H'),&{} \quad \hbox {if}\quad H = \bigcup H_{E} \wedge \exists \omega _{e} \in E, \varGamma {}(\omega _{e}, H)=0, \\ 1 - \sum _{H' \in H_{E}} \varGamma {}^{*}{}(E, H') &{} \quad \hbox {if}\quad H = \bigcup H_{E} \wedge \forall \omega _{e} \in E, \varGamma {}(\omega _{e}, H)>0, \\ \quad + \sum _{\omega _{e} \in E} \frac{\varGamma {}(\omega _{e}, H)}{|E|}, &{} \\ 0, &{} \quad \hbox {otherwise,} \end{array} \right. \end{aligned}$$

such that $H_{E} = \{ H' \subseteq \varOmega _{h} \mid \omega _{e} \in E, \varGamma {}(\omega _{e}, H') > 0 \}$ and $\bigcup H_{E} = \{ \omega _{h} \in H' \mid H' \in H_{E} \}$.

The value $\varGamma {}^{*}{}(E, H)$ from Definition 23 actually represents a complete evidential mapping for E and H as defined in [23] such that $\varGamma {}$ is a basic evidential mapping function. In particular, the first condition defines the mass for E and H directly from $\varGamma {}$ if each $\omega _{e} \in E$ implies H to some degree, i.e. if H is a projected focal element of each $\omega _{e} \in E$. In this case, the actual mass for E is taken as the average mass from the basic mapping for all supporting elements in E. The second condition then recursively assigns the remaining mass that was not assigned by the first condition to the set of possible hypotheses implied by E, i.e. the union of all projected focal elements for all $\omega _{e} \in E$. The third condition says that when H is a projected focal element of each $\omega _{e} \in E$ and when $H = \bigcup H_{E}$, then we need to sum the results from the first two conditions. Finally, the fourth condition just assigns 0 to all other subsets. Note that it is not necessary to compute the complete evidential mapping function in full since we are only interested in focal elements of $\mathsf {m}_{e}$.

Table 4 Evidential mapping $\varGamma {}$ from $\varOmega _{e} = \{ e_{1}, e_{2}, e_{3} \}$ to $\varOmega _{h} = \{ h_{1}, \ldots , h_{4} \}$

Example 6

Given the evidential mapping from Table 4 and a mass function $\mathsf {m}_{e}$ over $\varOmega _{e}$ such that $\mathsf {m}_{e}(\{ e_{2} \}) = 0.7$ and $\mathsf {m}_{e}(\varOmega _{e}) = 0.3$, then a mass function $\mathsf {m}_{h}$ over $\varOmega _{h}$ is the evidence propagated mass function from $\mathsf {m}_{e}$ with respect to $\varGamma {}$ such that $\mathsf {m}_{h}(\{ h_{1}, h_{2} \}) = 0.49$, $\mathsf {m}_{h}(\varOmega _{h}) = 0.3$ and $\mathsf {m}_{h}(\{ h_{4} \}) = 0.21$.

In terms of integrating uncertain sensor information into AgentSpeak, evidence propagation provides two benefits. Firstly, it allows us to correlate relevant mass functions that may be defined over different frames such that we can derive compatible mass functions which are suitable for combination. Secondly, it allows us to map disparate sensor languages into a standard AgentSpeak language, i.e. where each frame is a set of AgentSpeak belief atoms. For the remainder of this section, we will assume that evidence propagation has been applied and that any mass functions which should be combined are already defined over the same frame. However, in terms of decision-making (i.e. the selection of applicable plans), classical AgentSpeak is not capable of modelling and reasoning with uncertain information. As such, it is necessary to reduce the uncertain information modelled by a mass function to a classical belief atom which can be modelled in the agent’s belief base. For this purpose, we propose the following:

Definition 24

Let $\mathsf {m}_{}$ be a mass function over $\varOmega _{}$ and $0.5 < \epsilon _{\mathsf {BetP}_{}} \le 1$ be a pignistic probability threshold. Then, $\mathsf {m}_{}$ entails the hypothesis $\omega _{} \in \varOmega _{}$, denoted $\mathsf {m}_{} \models _{\epsilon _{\mathsf {BetP}_{}}} \omega _{}$, if $\mathsf {BetP}_{\mathsf {m}_{}}(\omega _{}) \ge \epsilon _{\mathsf {BetP}_{}}$.

When a mass function is defined over a set of belief atoms, the threshold $\epsilon _{\mathsf {BetP}_{}}$ ensures that at most one belief atom is entailed by the mass function. However, this definition also means that it is possible for no belief atom to be entailed. In this situation, the interpretation is that we have insufficient reason to believe that any belief atom in the frame is true. Thus, if no belief atom is entailed by a mass function, then we are ignorant about the frame of this mass function. In AgentSpeak, we can reason about this ignorance using negation as failure. While this approach is a drastic (but necessary) step to modelling uncertain sensor information in classical AgentSpeak, an extension to AgentSpeak was proposed in [3] which allows us to model and reason about uncertain beliefs directly. Essentially, for each mass function $\mathsf {m}_{}$, the pignistic probability distibution $\mathsf {BetP}_{\mathsf {m}_{}}$ would be modelled as one of many epistemic states in the extended AgentSpeak agent’s belief base, now called a global uncertain belief set (GUB). Using an extended AgentSpeak language, we can then reason about uncertain information held in each epistemic state using qualitative plausibility operators (e.g. describing that some belief atom is more plausible than another). For simplicity, we will not present this work in detail, but instead refer the reader to [3] for the full definition of a GUB.

Obviously, there is a computational cost associated with combination. For this reason, we introduce the following conditions to describe when information has changed sufficiently to warrant combination and revision:

Definition 25

Let S be a set of sources, $\varOmega _{}$ be a frame, $\mathsf {m}_{s_{}, t}$ be a mass over $\varOmega _{}$ from source $s_{} \in S$ at time t, and $\epsilon _{\mathsf {d}{}}$ be a distance threshold. Then, the context-dependent combination rule is applied at time $t + 1$ to the set $\{ \mathsf {m}_{s_{}, t + 1} \mid s_{} \in S \}$ if there exists a source $s_{}' \in S$ such that $\mathsf {d}{}(\mathsf {m}_{s_{}', t}, \mathsf {m}_{s_{}', t + 1}) \ge \epsilon _{\mathsf {d}{}}$.

This definition says that the context-dependent combination rule should only be applied when the information obtained from any one source has changed sufficiently (formalised by the distance threshold $\epsilon _{\mathsf {d}{}}$). However, to ensure that smaller incremental changes are not overlooked, it is still necessary to combine and revise information at some specified intervals. Thus, this definition just provides a method to minimise redundant computation.

In summary, integration with an AgentSpeak agent can be handled by a sensor information preprocessor or intelligent sensor which can perform the following steps:

• (i) Discount each mass function with respect to the source reliability degree $1 - \alpha$.

• (ii) Apply evidence propagation using evidential mappings to derive compatible mass functions for combination which are defined over AgentSpeak belief atoms.

• (iii) Combine relevant mass functions by applying the context-dependent combination rule if any source has returned sufficiently dissimilar information from the information previously recorded for that source.

• (iv) Derive a belief atom from the combined mass function and revise the AgentSpeak agent’s belief base with this new belief atom.

Note that even if information for some source does not need to be combined with information for another, then steps (i), (ii) and (iv) can still be performed to reflect the reliability of the source and to derive suitable AgentSpeak belief atoms.

5 Scenario: power grid SCADA system

This scenario is inspired by a case study on an electric power grid SCADA system used to manage power generation, transmission and distribution. In the power grid, system frequency refers to the frequency of oscillations of alternating current (AC) transmitted from the power grid to the end-user. In the UK, the frequency standard is 50 Hz and suppliers are obligated to maintain the frequency within a deviation of $\pm 1\,\%$. If demand is greater than generation, then frequency will decrease, but if generation is greater than demand, then frequency will increase. Thus, maintaining the correct frequency level is a load-balancing problem between power demand and power generation. In this scenario, the power grid is managed by a BDI agent encoded in AgentSpeak with a set of belief atoms, a set of primitive actions and a predefined plan library. With regard to frequency, the agent may believe the current level is low, normal or high (represented by belief atoms $\mathtt{freq(l)}{}$, $\mathtt{freq(n)}{}$ and $\mathtt{freq(h)}{}$, respectively). Examples of AgentSpeak plans in the agent’s plan library include the following:

P1 :

+!run_combiner : freq(n) $\mathtt{<-}$ !run_inverter; distribute_power; ...

P2 :

+freq(l) : true $\mathtt{<-}$ !generate_alert; !stop_combiner; !run_windfarm; ...

The plan P1 describes the steps that should be taken if the agent obtains the goal !run_combiner and also believes that the current frequency level is normal. These steps involve a new sub-goal !run_inverter and a primitive action distribute_power. On the other hand, the plan P2 describes the steps that should be taken when the agent obtains the belief that the current frequency level is low. In this case, the steps involve new sub-goals !generate_alert, !stop_combiner and !run_windfarm with the aim of increasing power generation.

Obviously, determining an accurate view of the current frequency level is vital for ensuring that the correct level is maintained. In this scenario, there are many sources of information which the agent may consult to determine the current level. For simplicity, we will focus on two main types of sources relevant to frequency. The first is sensors which provide numerical measurements of frequency levels from the set $\varOmega _{e}^{s} = \{ 48.7, 48.8, \ldots , 51.3 \}$. The second is experts which provide general estimations of frequency levels from the set $\varOmega _{e}^{e} = \{ \text {normal}, \text {abnormal} \}$. Information from both types of sources may be effected by uncertainty. For example, the accuracy of sensors may vary due to design limitations or environmental factors, experts may lack confidence in their estimations, and sources may be treated as unreliable due to previously incorrect information. In Table 5, we define evidential mappings from $\varOmega _{e}^{s}$ and $\varOmega _{e}^{e}$ to the set of AgentSpeak belief atoms $\varOmega _{h} = \{ \mathtt{freq(l)}{}, \mathtt{freq(n)}{}, \mathtt{freq(h)}{} \}$. These mappings allow us to combine different types of information and to derive suitable belief atoms for revising the agent’s belief base. Essentially the sensor mapping defines a fuzzy distribution over the range of possible sensor values, while the expert mapping defines a probabilistic relation between the abnormal estimation and the belief atoms $\mathtt{freq(l)}{}$ and $\mathtt{freq(h)}{}$ (assigning equal probability to each).

Table 5 Evidential mappings from $\varOmega _{e}^{s}$ and $\varOmega _{e}^{e}$ to $\varOmega _{h}$

Table 6 Information obtained from sources

Table 6a represents an illustrative scenario in which a number of sensors and experts have provided information about the current frequency level. Some sensor values have a deviation (e.g. $\pm 0.1$ Hz), while experts have expressed a degree of confidence in their assessment (e.g. 90 % certain). For example, source $s_{2}$ is a sensor which has determined that the frequency is 51.2 Hz with a deviation $\pm 0.1$ Hz, whereas $s_{5}$ is an expert which has estimated that the frequency level is abnormal with 90 % certainty. Moreover, each source has a prior reliability rating $1 - \alpha$ based on historical data, age, design limitations and faults, etc. Table 6a shows that $s_{1}$ is the most reliable source, while $s_{10}$ is the least reliable. In Table 6b, we can see how the information provided in Table 6a is modelled as mass functions and how these correspond to discounted mass functions, given their respective $\alpha$ values. For example, source $s_{1}$ has determined that the frequency is 51.2 Hz. By modelling this sensor information as a mass function $\mathsf {m}_{1}$, we have that a mass of 1 is assigned to the singleton set {51.2}. Alternatively, source $s_{10}$ has estimated that the frequency level is abnormal with 75 % certainty. By modelling this expert information as a mass function $\mathsf {m}_{10}$, we have that a mass of 0.75 is assigned to the singleton set {abnormal}, while the remaining mass is assigned to the frame $\varOmega _{}$. Each mass function is then discounted with respect to the reliability of the original source. For example, the source $s_{1}$ has a reliability of 0.98 and so the mass function $\mathsf {m}_{1}$ is discounted using a discount factor $\alpha = 1 - 0.98 = 0.02$. Finally, Table 6c provides the evidence propagated mass functions over $\varOmega _{h}$ with respect to Table 5 representing the compatible mass functions from each source.

Table 7 Finding LPMCSes in $\{ \mathsf {m}_{1}^{h}, \ldots , \mathsf {m}_{10}^{h} \}$ when $\epsilon _{\mathsf {K}{}} = 0.3$

In this scenario, we are not interested in the information provided by individual sources; rather, we are only interested in reasoning about the information as a whole. To achieve this, we must first combine the set of evidence propagated mass functions from Table 6c. Table 7 demonstrates how to apply the context-dependent combination rule on this set of mass functions by computing LPMCSes using an arbitrarily chosen conflict threshold $\epsilon _{\mathsf {K}{}} = 0.3$. Firstly, Table 7a provides the quality of information heuristics used to find a reference mass function. In this case, we select $\mathsf {m}_{1}^{h}$ as the reference since it has the minimum non-specificity and strife values. This mass function is then used to form a new (partial) LPMCS. Secondly, Table 7b provides the distance values between $\mathsf {m}_{1}^{h}$ and all other mass functions. From these, we select $\mathsf {m}_{3}^{h}$ as the next mass function in the preferred sequence of combination since it has the minimum distance to $\mathsf {m}_{1}^{h}$. Thirdly, referring to Table 7c we can see that the conflict between $\mathsf {m}_{1}^{h}$ and $\mathsf {m}_{3}^{h}$ is under the threshold meaning that $\mathsf {m}_{3}^{h}$ is added to the LPMCS and $\mathsf {m}_{1}^{h} \oplus {} \mathsf {m}_{3}^{h}$ becomes the new reference mass function. This process continues until we reach $\mathsf {m}_{5}^{h}$ where the conflict between $\mathsf {m}_{1}^{h} \oplus {} \ldots \oplus {} \mathsf {m}_{7}^{h}$ and $\mathsf {m}_{5}^{h}$ is above the threshold. Thus, the set $\{ \mathsf {m}_{1}^{h}, \ldots , \mathsf {m}_{4}^{h}, \mathsf {m}_{6}^{h}, \ldots , \mathsf {m}_{9}^{h} \}$ is the first LPMCS with respect to $\epsilon _{\mathsf {K}{}}$ and a new reference must be selected from the set $\{ \mathsf {m}_{5}^{h}, \mathsf {m}_{10}^{h} \}$. Referring again to Table 7a, we find that $\mathsf {m}_{5}^{h}$ is the highest quality mass function and select this as our new reference. Since $\mathsf {m}_{10}^{h}$ is the only remaining mass function, we just need to measure the conflict between $\mathsf {m}_{5}^{h}$ and $\mathsf {m}_{10}^{h}$ where we find that the conflict is below the threshold. Thus, the set $\{ \mathsf {m}_{5}^{h}, \mathsf {m}_{10}^{h} \}$ is the second LPMCS and the complete set of LPMCSes is $\mathsf {L^{*}}(\{ \mathsf {m}_{1}^{h}, \ldots , \mathsf {m}_{10}^{h} \}, 0.3) = \{ \{ \mathsf {m}_{1}^{h}, \ldots , \mathsf {m}_{4}^{h}, \mathsf {m}_{6}^{h}, \ldots , \mathsf {m}_{9}^{h} \}, \{ \mathsf {m}_{5}^{h}, \mathsf {m}_{10}^{h} \} \}$.

Table 8 Combined results

The combined mass function after applying the context-dependent combination rule on the set of mass functions, using an arbitrary conflict threshold $\epsilon _{\mathsf {K}{}} = 0.3$, is provided in Table 8a. In addition, the results for the full range of conflict thresholds $\epsilon _{\mathsf {K}{}} = 0, 0.01, \ldots , 1$ are shown graphically in Fig. 1. For comparison, the combined mass functions after applying Dempster’s rule and Dubois and Prade’s rule in full are also provided. Table 8b then includes the results for applying the pignistic transformation on these combined mass functions. Regarding these results, it is apparent that Dempster’s rule arrives at a very strong conclusion with complete belief in the belief atom $\mathtt{freq(h)}{}$. On the other hand, Dubois and Prade’s rule arrives at almost complete ignorance over the set of possible belief atoms $\varOmega _{h}$. The result of the context-dependent rule is arguably more intuitive since it does not throw away differing opinions (as is the case with the former) or incorporate too much conflict (as is the case with the latter). For example, after applying the context-dependent rule we can conclude that $\mathtt{freq(l)}{}$ is more probable than $\mathtt{freq(n)}{}$. Conversely, this conclusion is not supported using Dempster’s rule, while the support is relatively insignificant using Dubois and Prade’s rule. Nonetheless, the final stage of this scenario is to attempt to derive a belief atom for revising the agent’s belief base. In this case, if we assume a pignistic probability threshold $\epsilon _{\mathsf {BetP}_{}} = 0.6$, then we can derive the belief atom $\mathtt{freq(h)}{}$. If $\mathtt{freq(h)}{}$ is added to the agent’s belief base, then any plans with this belief addition event as their triggering event will be selected as applicable plans. Thus, the agent can respond by reducing power generation in order to return to a normal frequency level.

Fig. 1

Effect of varying the conflict threshold on $\mathsf {m}_{}(A)$ and $\mathsf {BetP}_{\mathsf {m}_{}}(\omega _{})$. a Effect of conflict threshold on $\mathsf {m}_{}(A)$, b effect of conflict threshold on $\mathsf {BetP}_{\mathsf {m}_{}}(\omega _{})$

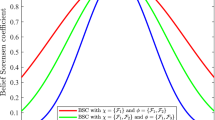
Figure 1 shows the effect of varying the conflict threshold and pignistic probability threshold. Figure 1a shows the mass values of focal elements after combining all relevant mass functions and for each conflict threshold $\epsilon _{\mathsf {K}{}} = 0, 0.01,\ldots , 1$. For example, when $\epsilon _{\mathsf {K}{}} = 0.1$, $\mathsf {m}_{}(\{ \mathtt{freq(h)}{}, \mathtt{freq(l)}{} \})=0.28$, $\mathsf {m}_{}(\{ \mathtt{freq(h)}{} \})=0.093$, $\mathsf {m}_{}(\varOmega _{})=0.627$. When $\epsilon _{\mathsf {K}{}} \le 0.18$, the context-dependent combination rule results in three LPMCSes $\{ \{ \mathsf {m}_{1}^{h}, \ldots , \mathsf {m}_{4}^{h}, \mathsf {m}_{6}^{h}, \ldots , \mathsf {m}_{9}^{h} \}$, $\{ \mathsf {m}_{5}^{h} \}$, $\{ \mathsf {m}_{10}^{h} \} \}$, where $\varOmega _{h}$ is assigned the highest combined mass value. In contrast, when a conflict threshold is in the interval [0.19, 0.38], the context-dependent combination rule results in two LPMCSes $\{\{ \mathsf {m}_{1}^{h}, \ldots , \mathsf {m}_{4}^{h}, \mathsf {m}_{6}^{h}, \ldots , \mathsf {m}_{9}^{h} \}, \{ \mathsf {m}_{5}^{h}, \mathsf {m}_{10}^{h} \} \}$. In this case, $\varOmega _{h}$ has the lowest combined mass value, while the other focal sets are assigned equal combined mass values. Furthermore, when $\epsilon _{\mathsf {K}{}} \ge 0.39$, the context-dependent combination rule results in one LPMCS, i.e. $\{ \{ \mathsf {m}_{1}^{h}, \ldots , \mathsf {m}_{10}^{h} \}\}$, where $\{ \mathtt{freq(h)}{} \}$ is assigned a combined mass value of 1. In this case, the context-dependent combination rule reduces to Dempster’s rule. Conversely, in this scenario, the context-dependent combination rule never reduces to Dubois and Prade’s rule since, even when $\epsilon _{\mathsf {K}{}} = 0$, we never have a set of singleton LPMCSes. Notably, as the conflict threshold increases, the mass value of $\{ \mathtt{freq(h)}{} \}$ increases, while the mass value of $\varOmega _{h}$ decreases. However, the mass value of $\{ \mathtt{freq(l)}{}, \mathtt{freq(h)}{} \}$ fluctuates (i.e. increasing first before decreasing). In particular, the mass value increases in the interval [0, 0.38], due to the mass value of $\varOmega _{h}$ being shifted to strict subsets. By comparing the results from Figure 1a, we can conclude in this scenario that a conflict threshold in the interval [0, 0.38] will offer a balance between both rules such that our rule does not reduce to one rule or the other. Figure 1b shows the corresponding pignistic probability distribution after applying the pignistic transformation on the combined mass function to demonstrate the effect of varying the conflict threshold on decision-making. For example, when $\epsilon _{\mathsf {K}{}} = 0.1$, $\mathsf {BetP}_{\mathsf {m}_{}}(\mathtt{freq(h)}{})=0.442$, $\mathsf {BetP}_{\mathsf {m}_{}}(\mathtt{freq(l)}{})=0.349$, $\mathsf {BetP}_{\mathsf {m}_{}}(\mathtt{freq(n)}{})=0.209$. As can be seen, when the conflict threshold increases, the probability assigned to $\mathtt{freq(h)}{}$ increases, while the probability of $\mathtt{freq(l)}{}$ and $\mathtt{freq(n)}{}$ decreases. By comparing the probability distributions in Figure 1b, it indicates $\mathtt{freq(h)}{}$ is the obvious conclusion for deriving a belief atom for decision-making. However, the choice of thresholds will affect whether a belief atom is actually derived. Specifically, if $\epsilon _{\mathsf {BetP}_{}} \le 0.7$ and $\epsilon _{\mathsf {BetP}_{}} \ge 0.2$, then $\mathtt{freq(h)}{}$ will be derived; otherwise, nothing will be derived. This demonstrates the benefit of our rule since relying on Dubois and Prade’s rule alone would not allow us to derive a belief atom, while Dempster’s rule loses potentially useful uncertain information.

6 Conclusion

In this paper we presented an approach to handling uncertain sensor information obtained from heterogeneous sources for aiding decision-making in BDI. Specifically, we adapted an existing context-dependent combination strategy from the setting of possibility theory to DS theory. As such, we proposed a new combination strategy which balances the benefits of Dempster’s rule for reaching meaningful conclusions for decision-making and of alternatives, such as Dubois and Prade’s rule, for handling conflict. We also proposed an approach to handle this sensor information in the AgentSpeak model of the BDI framework. In particular, we described the formulation of an intelligent sensor for AgentSpeak which applies evidence propagation, performs context-dependent combination and derives beliefs for revising the agent’s belief base. Finally, in Sect. 5 we demonstrated the applicability of our work in terms of a scenario related to a power grid SCADA system. An implementation of the work presented in the paper is available online.⁵