Abstract
The widespread availability of high spatial and temporal resolution public transit data is improving the measurement and analysis of public transit-based accessibility to crucial community resources such as jobs and health care. A common approach is leveraging transit route and schedule data published by transit agencies. However, this often results in accessibility overestimations due to endemic delays due to traffic and incidents in bus systems. Retrospective real-time accessibility measures calculated using real-time bus location data attempt to reduce overestimation by capturing the actual performance of the transit system. These measures also overestimate accessibility since they assume that riders had perfect information on systems operations as they occurred. In this paper, we introduce realizable real-time accessibility based on space–time prisms as a more conservative and realistic measure. We, moreover, define accessibility unreliability to measure overestimation of schedule-based and retrospective accessibility measures. Using high-resolution General Transit Feed Specification real-time data, we conduct a case study in the Central Ohio Transit Authority bus system in Columbus, Ohio, USA. Our results prove that realizable accessibility is the most conservative of the three accessibility measures. We also explore the spatial and temporal patterns in the unreliability of both traditional measures. These patterns are consistent with prior findings of the spatial and temporal patterns of bus delays and risk of missing transfers. Realizable accessibility is a more practical, conservative, and robust measure to guide transit planning.
Similar content being viewed by others
1 Introduction
Accessibility, or the ability to reach opportunities in an environment, is a fundamental concept in transportation science and human geography (Hansen 1959; Ingram 1971). As the focus of transportation planning shifts to a sustainable mobility paradigm, accessibility measures are becoming more crucial as a performance measure to guide policy, planning, and decision-making (Banister 2008). Advances in mobility and geospatial data technologies and science have enhanced the sophistication and practicality of accessibility measures to a point that they are transforming planning and policy (Handy 2020; Levinson & Wu 2020; Wu & Levinson 2020). This includes the space–time prism (STP): a core concept in time geography that models accessibility as the envelope of all possible paths with respect to time based on anchoring locations and times, maximum speeds for travel, and stationary activity times (Hägerstrand 1970). New mobility and geospatial data technologies have allowed researchers to greatly increase the analytical power of this basic time geographic concept (Miller 2017; Neutens et al. 2007).
O’Sullivan et al. (2000) pioneered the application of STPs to model public transit accessibility. Since that time, the availability of data on public transit networks and related supporting infrastructure such as sidewalks afforded the development of public transit network accessibility analysis based on high-resolution representation of transit and walking networks. However, this research traditionally still depended on assumptions of average schedule frequency and headways during peak and off-peak times (Tribby & Zandbergen 2012). This barrier has been shattered by the development of data standards for publishing high-resolution schedule and real-time vehicle location data public transit data via the General Transit Feed Specification (GTFS) developed by Google. GTFS allows developers to create navigation apps to support public transit users. It is also allowing researchers to analyze the accessibility generated by public transit systems at high levels of spatial and temporal resolution (Lee & Miller 2018; Wessel et al. 2017; Wessel & Farber 2019).
Transit systems are highly dynamic and time dependent due to variations in operating conditions, and actual performance can be different from the schedule (Park et al. 2020). There are several factors that contribute to these deviations from scheduled service: first, many bus systems operate within road networks that are shared with other vehicles. Conditions such as recurrent congestion and non-recurrent disruptions like construction and crashes can slow transit vehicles, leading to deviations from the scheduled service. Second, only travel time at designated timepoint benchmark stops is explicitly defined in the official timetables of many transit systems; travel time at non-timepoint stops is derived from interpolation, which may not be strictly followed in practice.
Wessel et al. (2017) and Wessel & Farber (2019) compared accessibility measures based on public transit schedule data with accessibility measures calculated retrospectively from real-time vehicle location data, finding substantial differences that call into question the use of schedule data alone for public transit accessibility analysis. However, while retrospective real-time accessibility measures recognize that actual operations can deviate from scheduled service, they assume users know a priori the actual arrival time of vehicles (Wessel & Farber 2019); this knowledge is only attainable after the event happens. This makes accessibility measures calculated retrospectively from real-time vehicle location data unrealistic in depicting the accessibility realized by the transit system and experienced by public transit users.
This paper provides a scalable time geography approach to measure the reliability of transit accessibility. We introduce the concept of realizable real-time accessibility based on the STP to address the overestimation of accessibility in traditional measures. Like retrospective real-time accessibility, the realizable real-time accessibility is also calculated based on actual bus locations data, but it acknowledges that users are not able to know the actual arrival times a priori and respond in real-time to on-time performance deviations in the network. We also introduce the concept of accessibility unreliability as a measure of the deviation of schedule accessibility or retrospective accessibility from realizable accessibility. This measure represents the difference between the expected potential path area (PPA)—i.e., the spatial footprint of the STP—and the actual or realized PPA based on realistic system performance given the same time budget and departure time. The aggregate version of this measure can also show the consistency and reliability of the transit service; this is vital for administrative and planning purposes. We use schedule and real-time vehicle location data to calculate and compare STPs based on schedule, retrospective, and realizable real-time accessibility assumptions. We illustrate these measures using GTFS data from the Central Ohio Transit Authority (COTA) bus system, a public transit agency in Columbus, Ohio, USA. The analyses focus on the spatial and temporal patterns in different levels from 2018 to 2019 across Columbus.
In the next section of the paper, we discuss the background of the space–time prism, transit accessibility, and the unreliability issue of accessibility measures. We then introduce the data source; the time-dependent routing algorithm; the concepts of scheduled, retrospective real-time, and realizable real-time STP; and accessibility unreliability in the methodology section. We finally discuss the findings of overall distinction, spatial, and temporal analyses in the results section.
2 Background
This section provides background for the concepts and measures of realizable real-time accessibility and accessibility unreliability. We discuss: (1) the evolution of the space–time prism; (2) the development of transit accessibility measurements; and (3) the unreliability of schedule-based accessibility measures.
2.1 The evolution of the space–time prism
The space–time prism (STP) is a well-established time geography method to measure physical accessibility afforded by transportation systems (Miller 1991; Wu & Miller 2001). Since its introduction by Hägerstrand (1970) as a concept, there has been progress in STP analytics based on improving capabilities of computer hardware and software, and the availability of data, allowing the STP to be operationalized and measured more realistically. Lenntorp (1976) provided the first operational implementation of the STP in his computer simulation of possible activity and travel schedules. Burns (1980) provided an analytical foundation for the STP in his formal analysis of the impacts of time, speed, and network changes on accessibility. The rising popularity of geographic information system (GIS) software inspired Miller (1991) to develop a generic GIS-based procedure to derive STPs within transportation networks. Refinements in capabilities for calculating shortest paths from and to arbitrary locations within networks allowed Miller (1999) to refine the STP within transportation networks. Increasing availability of dynamic network data allowed researchers to develop procedures for calculating STPs within networks with time-varying flows and travel times (Li et al. 2011; Wu & Miller 2001).
Improvements in location-aware technologies such as the global positioning system (GPS), automated vehicle location (AVL) devices, and mobile telephony have also allowed greater refinement and wider application of the STP. Abundant data help refine STP models and enhance the reliability of STP measures. For example, Chen et al. (2013) used floating-taxi traffic data to introduce travel time uncertainty into the calculation of the STP. Delafontaine et al. (2011) introduced a STP framework with emphasis on travel time uncertainty in non-network-constrained environments. Chen et al. (2016) address the scalability of STP to large-scale applications and data through an efficient spatiotemporal data model. Abundant data can also help extend the applicability of STP and time geographic models to wider domains. For example, Fang et al. (2012) utilized STP to identify crucial links from a large origin–destination trips dataset. Farber et al. (2015) used social interaction potential and the space–time prism to measure the spatial and temporal dynamics of social segregation. Li & Farber (2016) used social interaction potential to explore the role of the modifiable areal unit problem in time geographic accessibility measures. Widener et al. (2015) used the social interaction potential to measure and compare food access by automobile and public transit.
2.2 The evolution of transit accessibility measurement
Malekzadeh & Chung (2020) suggest there are two major trends for transit accessibility studies: (i) better capturing travelers’ behavior and (ii) developing more disaggregated transit accessibility measurements. Both trends exemplify how larger, more detailed, and more accessible datasets impact the formulation of transit accessibility models.
Due to its multimodal and nonlinear nature, early transit accessibility models usually adopt simple assumptions based on travel time estimations, which significantly reduces their computational burden (Malekzadeh & Chung 2020). For example, some early transit accessibility models consider the proximity to transit stops by only walking as the accessibility to a transit system (Hsiao et al. 1997; Zhao et al. 2003), which is a major simplification since they ignore the travel time in the transit system. As transit-related datasets become more detailed and accessible, models can better capture the travelers’ behavior, such as system-facilitated models—i.e., measuring users’ ability to reach other opportunities in the transit network (Tribby & Zandbergen 2012) and integral accessibility models—i.e., measuring overall access to a number of possible destinations (Farber et al. 2014; Owen & Levinson 2015). As mentioned in introduction of this paper, O’Sullivan et al. (2000) pioneered the application of STPs in the analysis of public transit accessibility. However, their analysis assumes travel through planar space outside the transit network. Tribby & Zandbergen (2012) improved transit accessibility by incorporating detailed representations of the sidewalk network for traveling to, from and between transit stops. However, their analysis assumes a static or steady-state transit headway for peak and off-peak hours, based on scheduled service frequency. More detailed and specific models powered by high-resolution and large-volume real-time data can provide a better understanding of transit accessibility.
Another trend in transit accessibility analysis is more disaggregated transit accessibility measurements. For example, while traditional studies mainly addressed accessibility at the regional level and stop level (O’Sullivan et al. 2000; Tribby & Zandbergen 2012), recent studies can assess trip-level or even person-level accessibility based on fine-grained standard data like General Transit Feed Specification (GTFS) and smart card data (Arbex & Cunha 2020; Batty 2013; Lee & Miller 2018). These data have well-defined structures for scheduled information, real-time bus location and time, or trip behavioral information; GTFS data are also often released publicly by transit authorities (Barbeau & Antrim 2013). Therefore, many recent studies use GTFS to derive STP at a larger scale without compromising the fine details of transit systems (Lee & Miller 2018; Tasic et al. 2014). Meanwhile, more powerful computational platforms are also making accessibility modeling significantly more detailed. For example, OpenTripPlanner uses a multimodal routing engine to provide refined results of accessibility at specific times and locations (Boisjoly & El-Geneidy 2017; Owen & Levinson 2015). Larger and more-detailed datasets, greater computational ability, and better visualization methods help to improve the fidelity and granularity of transit accessibility analysis.
2.3 Unreliability of schedule-based accessibility measures
As recent studies focus more on capturing users’ stochasticity, unreliability becomes the center of the discussion: in other words, how well can an accessibility measurement capture the actual experience of a user in the system? We define unreliability as an accessibility measurement’s deviation from a standard benchmark, which ideally should represent the accessibility delivered to or experienced by users. Due to the lack of accessible real-time data sources, most traditional accessibility measures are calculated based on transit schedules (Wessel & Farber 2019); therefore, many schedule-based accessibility measures can be unreliable due to two factors: uncertainty and accuracy.
Uncertainty refers to the stochastic variation in the accessibility measure, due to on-time performance and measurement error. Public transit systems are constantly changing, with early or late arrival times occurring because of unexpected external or internal factors, such as traffic, weather, vehicle conditions, or operator conditions. Hall (1983) was among the first to consider uncertainty when formulating and calculating accessibility. Similar to the development of STP, more studies are being dedicated to discussing the unreliability of accessibility measures with better datasets. For example, Kim & Song (2018) discuss an integrated measure of accessibility and reliability for transit systems; Zhang et al. (2018) introduce a time-dependent reliability modeling approach based on GPS trajectories to address traditional measures’ overestimation problem. More recently, a new R5 routing engine can simulate the uncertainties of travel time with static GTFS feeds (Conway et al. 2018; Pereira et al. 2021).
Another factor that can contribute to a schedule-based accessibility measure’s unreliability is accuracy. It can be defined as systematic deviations of an accessibility measure from the standard benchmark. Some papers discussed the topic with empirical evidence: Wessel et al. (2017) constructed a retrospective transit timetable from real-time automatic vehicle location data to better capture the dynamic nature of the transit system. The paper also provided a case study for the Toronto Transit system and pointed out that an accessibility measure based on retrospectively collected real-time vehicle locations data does have significant deviation from the schedule, and the pattern of the deviation does not seem random. Wessel & Farber (2019), moreover, explored the accuracy of schedule-based accessibility in Toronto, Jacksonville, Massachusetts Bay, and San Francisco. The paper concludes that schedule-based accessibility measures overestimate on average by five to 15 percent or more, and it may not be sufficient to use schedule data alone to evaluate transit accessibility for most transit systems.
Traditional schedule-based accessibility measures have both uncertainty and accuracy issues. In the following sections, we continue the discussion of schedule-based unreliability issues; we also expand the discussion to examine unreliability issues in retrospective accessibility measures.
3 Methodology
In this section, we introduce the definition of accessibility and unreliability. We first introduce the two main transit datasets on which our analysis is based. Then, we demonstrate a time-dependent Dijkstra algorithm to calculate the two versions of space–time prisms.
3.1 Data sources
We use General Transit Feed Specification (GTFS) data as the main data source for time geographic analyses in this paper. GTFS is a data standard that helps transit authorities to publish transit data and developers/researchers to consume the data (Google Developers 2020). GTFS includes two parts: GTFS static and GTFS real-time data, corresponding to scheduled service and real-time vehicle locations, respectively. Several relational database tables comprise the GTFS static data, specifying the transit system’s stops, trips, routes, arrival and departure time, and other schedule information (Google Developers 2020). The GTFS real-time data include two parts: trip update, which contains the expected arrival/departure time of each trip at each stop in the transit system, and vehicle position, which is similar to automatic vehicle location (AVL) data and shows the location of active vehicle in the system (Google 2021). Transit authorities broadcast GTFS real-time data at regular time intervals from 10 to 90 s to support navigation apps (Liu & Miller 2020a). We derived the actual arrival time of each trip at each stop from the latest trip update feeds.
We collected both GTFS static and real-time trip update data from the official application programming interface (API) of the Central Ohio Transit Authority (COTA) from February 2018 to March 2020 (Central Ohio Transit Authority 2021). We record the updated GTFS static data whenever there are any changes in the schedule data. This can include minor changes on a daily basis, three seasonal adjustments in January, May, and September, major planned route and schedule changes, such as COTA transit system redesign in May 2017 (Lee & Miller 2018; Schmitt 2018) and COVID-19-related schedule adjustments in 2020 (Liu et al. 2020). We collected real-time trip update feeds at the interval of 60 s; this is a common GTFS real-time update frequency for US transit systems (Liu & Miller 2020a). The total data volume exceeds one terabyte. Due to the large data size, we used a noSQL (unstructured) database technology, MongoDB, to maintain the database and support queries.
3.2 Time-dependent routing
We use the STP, a well-established time geography method, to measure accessibility in public transit systems (Miller 1991; Wu & Miller 2001). In practice, we first calculate the shortest travel time between the origin stop and all other stops in the system. We then derive the STP and its spatial footprint, the PPA, by finding the set of stops for which the travel time is no greater than a specified time budget.
It can be challenging to obtain accurate travel times in a transit network, even with a complete archive of retrospective arrival times. A major reason is because transit networks are discontinuous and time-dependent (Gendreau et al. 2015; Wang et al. 2019). Unlike private vehicle or pedestrian network, a user cannot move in the network until he or she boards a vehicle which arrives only at specific time points. Therefore, the network costs of transit can vary depending on the passenger’s arrival time at the originating stop of a transit system. This time-dependent variation also applies to other components of public transit travel times, including wait time and in-vehicle time.
There are two approaches to time-dependent routing: deterministic and stochastic (Gendreau et al. 2015). Stochastic models include a random factor to predict the time-varying travel times. They are useful at capturing the randomness caused by congestion, weather, crashes, and road maintenance (Gendreau et al. 2015); however, because we already empirically collected the actual arrival times at all the stops and aim for more precise travel time measures, we use a deterministic approach to address the time-dependent routing problem.
We use a Dijkstra algorithm with dynamic costs to solve the time-dependent routing problem. The Dijkstra algorithm is a classic and efficient algorithm to solve the shortest path routing problem (Golden 1976). It uses a greedy strategy to find the shortest path from the origin node to every other node (Xie et al. 2012), which significantly reduces the size of the subproblems and is very useful and efficient to calculate the STPs. However, the correctness of the Dijkstra algorithm is based on non-negative static costs that time-dependent transit networks do not satisfy. In particular, a vehicle with a later start time may result in an earlier arrival time than another vehicle if the first vehicle passes the second (Gendreau et al. 2015). Consequently, the results generated by Dijkstra algorithm with dynamic costs may not be the globally optimal solution. Therefore, many prior studies introduced no-passing or first-in-first-out (FIFO) rule to make the Dijkstra algorithm compatible with the time-dependent requirements (Ahn & Shin 1991; Ichoua et al. 2003). FIFO rule assumes a vehicle leaving an origin stop will never arrive later at the destination stop than another vehicle that departed later. FIFO rule is a prerequisite to use Dijkstra to calculate the routing problem in a transit system. Therefore, we tested if vehicles in the COTA system satisfy the FIFO rule by calculating whether each bus in the transit system can indeed pass subsequent buses in the same route. The average proportion of no-passing buses is 95%; therefore, we conclude that there are very few passing occurrences in the COTA system, and the FIFO rule generally applies to the system.
3.3 Three space–time prisms
After calculating the time-dependent shortest travel time between any stops in the system based on the scheduled and retrospective GTFS data, we derive an implicit STP by calculating the number of accessible bus stops. We use a decision variable \(\delta_{ij\tau }^{\phi }\) to represent whether a user starting from stop \(i\) at time point \(t\) can arrive at another stop \(j\) within the time budget \(\tau\):
where \(t_{ij}^{\phi }\) is the shortest travel time between stops \(i\) and \(j\) starting from a time point \(\phi\). Therefore, the number of accessible stops with the time budget \(\tau\) can be written as:
where \(s_{i\tau }^{\phi }\) represents the number of accessible bus stops (or an implicit PPA of the STP) from stop \(i\) at the time point \(t\) with the time budget \(\tau\) and \(S\) is the set of all stops. We can then introduce the definition of the STP:
where \(S_{i}^{\phi }\) represents the implicit STP from stop \(i\) at a time point \(\phi\), while \({\text{T}}\) is the set of all time budgets.
We produce three versions of the bus stop-based implicit STPs based on the shortest travel times, namely scheduled, retrospective real-time, and realizable real-time STPs.
3.3.1 Scheduled STP
Scheduled STPs are calculated based on the scheduled time from the GTFS static dataset. It represents the expected accessibility that a passenger can achieve if the transit system operates perfectly according to the schedule. However, the actual travel time and accessibility may vary due to on-time performance deviations, and schedule is not an unbiased representation of a transit system’s actual performance (Park et al. 2020); therefore, the scheduled STP is typically an overestimate of the actual accessibility experienced by a passenger.
3.3.2 Retrospective real-time STP
As we can access all the historical arrival times from the GTFS real-time archive, we can calculate a retrospective version of the STP using the same algorithm described above by changing all the scheduled arrival times to corresponding retrospective real-time arrival times (Wessel et al. 2017; Wessel & Farber 2019). Although this allows for deviation from the schedule STP, it is still idealistic. When planning trips, the user cannot know a priori the actual arrival time of each bus (Wessel & Farber 2019). Although it can be a useful reference for transit agencies and users, the retrospective real-time STP, or more generally retrospective real-time accessibility, cannot be realized by users. It overestimates users’ accessibility because it assumes users have omniscient knowledge of the transit system, even events that happen in the future. There are some unnatural and infeasible results caused by this overestimation: in the retrospective model, a user can decide to take a very different combination of trips and routes that will not be possible without predicting the future.
For example, Fig. 1 shows a real-world routing example based on COTA data that illustrates the overestimation potential for retrospective accessibility to overestimate caused by a preemptive transfer when the receiving bus that the user will transfer to is delayed (Liu & Miller 2020b). The map shows two retrospective- and schedule-based routes; the retrospective route saves one transfer and much time compared to the scheduled scenario by taking a different bus at the circled stop. This was only possible for the retrospective scenario because the incoming bus in the alternative second leg (route 101, colored pink with origin stop circled) was delayed by four minutes relative to the schedule. However, unless the transit user can predict the future or have perfect real-time information feeds, it is almost impossible to foresee this transfer is possible.
An example of overestimation in retrospective route (red, with two legs) compared to scheduled route (blue, with three legs). A delayed bus on the retrospective route’s second leg (pink, origin stop circled) makes the transfer feasible, which is impossible in the scheduled timetable and very hard for normal users to anticipate
We can, moreover, deconstruct scheduled and retrospective real-time accessibility from a perspective of a user’s decision-making: these two accessibility systems do not separate the decision-making and the decision implementation process. For a user, the decision-making process typically happens before the implementation process since people plan their trips before taking the transit, and the implementation result can be different from what they plan. However, both schedule and retrospective real-time accessibility models assume the two processes are happening simultaneously: the users are assumed to always realize the expected trip plan and never miss a bus. Such an assumption is unrealistic because users are likely to miss a bus and suffer additional time penalty in reality, especially during transfers when users have no control over the buses (Liu & Miller 2020b; Park et al. 2020).
3.3.3 Realizable real-time STP
Because of the unrealizable nature of both schedule and retrospective real-time accessibility models, we therefore define realizable real-time STP, or more generally realizable real-time accessibility, based on realizable real-time shortest travel time between any stops. We calculate realizable real-time shortest travel time in two steps to better represent transit users’ actual decision-making process: planning and implementation.
The first step is planning. We calculate a hypothetical user’s trip plan from the scheduled timetable, including all the shortest travel time and the corresponding route choice assuming buses follow the schedule. We assume that users do not have access to real-time information (RTI) about public transit since we want to define realizable real-time accessibility as a conservative estimate of experienced accessibility. In addition, from a social equity perspective, RTI may not be accessible for everyone since smartphone and broadband Internet access are not universal (Mohadisdudis & Ali 2014; Tsetsi & Rains 2017).
The second step is implementation. The results of the planning step show how users or their trip planning app expect their trips will be, but the actual outcome can vary depending on the system’s actual on-time performance. Therefore, we revisit the same route choice plan from the planning step; we find the actual travel time between each arc and actual arrival time at each node on the planned route from the real-time transit data. This means the trajectories of scheduled and realizable real-time STP are the same, but they can have different travel times. For example, the trajectory is {A, B, C} in the trip plan between A and C, where A, B, C represent a sequence of stops. The user is scheduled to take bus 1 from stop A to B, then transfer at stop B to another bus 2, and finally arrive at stop C. However, because bus 1 is delayed, the user arrives late at the transfer stop B and misses the scheduled transfer bus 2. We then find the next bus from stop B to C and record the new arrival time at stop C and travel time between stops A and C. Note that the user will not follow alternative routes, since users plan their route fully based on the schedule and the freedom of switching routes during the trip is limited.
There are several factors that contribute to differences between the retrospective and realizable real-time STPs: (i) unlike the retrospective accessibility, a user does not have to experience the trip itself to make the decision about the trip, and it is calculated from information that can be obtained before the trip happens. Therefore, it is realizable; (ii) delayed or early arrival at the origin stop and transfer stops can result in substantial delay times for longer trips that involve multiple transfers; (iii) routes calculated retrospectively can exploit shortcuts that result in reduced travel times compared to the scheduled routes as shown in Fig. 1; however, real-world users cannot anticipate these shortcuts.
From the perspective of information veracity, we can consider retrospective accessibility as the measure that requires perfect RTI input for user decision-making, which can fully foretell the future states of the network. Conversely, we can consider realizable accessibility as the measure with no RTI input, which can not anticipate future states of the network. Therefore, we view the retrospective and realizable STP as the upper bound and lower bound of accessibility, respectively. Other accessibility measures with different RTI-based predicting schemes or routing algorithms should produce STPs that fall between the two benchmarks. For the same reason, although we use realizable real-time STP as a relaxed benchmark in this study, we do not claim the realizable measure can fully reflect all transit users’ behavior and can be a universally authoritative benchmark for all purposes. Many other routing algorithms adopt different assumptions and conditions, which almost guarantee their results will be different (further discussed in Sect. 4.2).
Figure 2 illustrates six possible relationships among the three STPs. The realizable accessibility should always be the smallest of the three, while the retrospective accessibility can be equal to, larger than, or smaller than the scheduled accessibility depending on the network geometry and on-time performance.
3.4 Accessibility unreliability
We define accessibility unreliability as the difference between expected (scheduled STP and retrospective real-time STP) and the delivered accessibility measures (realizable real-time STP). Based on the STP definition provided in Eq. (3), we define accessibility unreliability as:
where \(S_{i}^{\phi }\) is the expected STP (schedule or retrospective) starting from a time point \(\phi\), \(R_{i}^{\phi }\) is the realizable STP, \(s_{i\tau }^{\phi }\) is the expected number of accessible stops, and \(r_{i\tau }^{\phi }\) is the realizable number of accessible stops. We calculate two versions of accessibility unreliability: scheduled STP’s unreliability and retrospective real-time STP’s unreliability. Scheduled STP is the promise that the transit authorities make to users, while the realizable STP is the actual experience the transit system delivers. The difference between the two represents the part of accessibility the transit system loses during operation compared with the schedule.
4 Analysis
In this section, we apply the methods above to empirical schedule and real-time data for the transit network in Columbus, Ohio. We first discuss the general differences between the scheduled, retrospective, and realizable STPs. We then show the spatial pattern of accessibility unreliability for different time budgets. Finally, we analyze the temporal pattern of accessibility unreliability in multiple dimensions.
4.1 Overall differences between three STPs
We first illustrate a specific scenario to demonstrate differences among the three STPs. Figure 3 shows an example of the PPAs corresponding to scheduled, retrospective, and realizable STPs with different time budgets from a bus stop in downtown Columbus at 8:00am on 4 September 2019. We can see that the schedule and retrospective PPAs resemble each other spatially, while the realizable STP is more circumscribed. Figure 3 (lower right quadrant) overlays the three STPs’ PPAs for a time budget of 30 min (also highlighted in other three maps in Fig. 3) at the same origin stop and the same time. This illustrates that schedule and retrospective accessibility may be different from each other in terms of their spatial footprint, but they are nevertheless a generous delimitation of accessibility compared to the more conservative realizable STP.
Examples of scheduled (top left), retrospective (top right), and realizable space-time-prisms (STPs) (bottom left) from a bus stop in the central downtown Columbus (North High Street & West Broad Street) at 8:00am, Sep 4, 2019, and overlaying potential path areas (PPAs) (highlighted) for the time budget of 30 min from the three STPs (bottom right)
Figure 4 shows the global average trend of the three measures. The plot shows the number of accessible stops as a function of the time budget. The plot clearly shows how the realizable measure is consistently smaller and a more conservative estimate of accessibility than the other two. Another notable observation is that the retrospective and schedule measures are similar, and the retrospective measure is sometimes greater and sometimes smaller than the schedule measure. This phenomenon illustrates that if a user is given perfect real-time information in a way that they can fully predict the future, the user can achieve comparable accessibility to that promised by the schedule and can even exceed it in some cases despite the existence of system delay. However, it is impossible to get perfect predictive real-time information in practice. The similarity of scheduled and retrospective measures may seem counterintuitive based on the dissimilarity of the two measures in Fig. 3; however, it should be noted that (1) Fig. 4 represents the average of the STPs for all stops while Fig. 3 shows the STP for only one stop, and (2) the aggregated numbers of accessible stops for the scheduled and retrospective are still indeed similar, despite dissimilarity of their shapes.
4.2 Spatial pattern of accessibility unreliability
We present results from analyzing the unreliability of schedule-based accessibility, using the realizable accessibility measure as a benchmark (Eq. (4)). Figure 5 shows four maps of schedule-based implicit STP’s unreliability with respect to the realizable measure for each stop for time budgets of 15, 30, 60, 90 min for the last four months in 2019. Note that the map does not visualize a single STP; instead, the map summarizes more than 3000 STPs to their corresponding anchor (i.e., origin bus stop), showing the unreliability of each STP originating from each stop. The percentage can be interpreted as the scheduled-based measure’s deviation from the realizable measure (see Eq. (4)), therefore representing the inaccuracy or overestimation of the scheduled-based measure. For example, 0% means no overestimation at all and the scheduled-based measure is the same as the realizable measure, while 100% means the scheduled-based measure is twice as much as the realizable measure.
We can see from the maps that the spatial pattern of accessibility unreliability is highly dependent on the time budget: for smaller budget of 15 min, unreliability concentrates on the city center; for bigger and more practical time budgets for longer trips of 30–60 min, unreliability gradually spreads to a larger area until it affects almost all stops in the system. For relatively large time budgets, unreliability of schedule-based accessibility starts to decrease from the center and becomes more concentrated in the periphery. We call this phenomenon saturation. As the PPA expands to include the whole system with larger time budgets, the scheduled PPA component in Eq. (4) will not be larger since the system has finite number of bus stops and it reaches a maximum value; however, the realizable PPA item will continue to rise, making the unreliability index smaller. Similar phenomena have been observed in prior studies (Wessel & Farber 2019).
Figure 6 depicts the average scheduled-based unreliability as a function of time budget for four classes of stations based on their distance to the city center (downtown core, and inner, middle and outer rings) and also the global average. The saturation process is evident; all curves first increase and reach a peak, then decrease as the time budget becomes large enough for schedule-based accessibility to include the entire network. However, depending on the geographic location of the stop, the time budget for peak unreliability will be different: the time budget where the peak occurs is directly correlated with the distance of the stops from the city center. This supports the pattern observed in Fig. 5 in which the high unreliability cluster migrates outward from the city center as time budget increases. We speculate that this phenomenon may be due to the star-shaped route alignment and transfer-focus planning strategy of the COTA bus system, since most unreliability comes from time penalty of missing a transfer (Liu & Miller 2020b, a). Moreover, as longer trips require more than one transfer, the total transfer time penalty will be larger due to a chain reaction effect.
It is noteworthy that our conclusions in the two sections above are seemingly different from the findings in Wessel et al. (2017) and Wessel & Farber (2019) despite using a similar cumulative opportunities approach to measure accessibility. There are several explanations for this contradiction: (1) the realizable accessibility measure is essentially a different measure from the retrospective accessibility used in those studies; (2) we use a different routing algorithm; (3) Wessel et al. (2017) observed that their retrospective measure was similar to schedule-based accessibility on average, which is consistent with our findings; (4) Wessel & Farber (2019) only select one specific long time budget (cumulative parameter) for geographic visualizations, while we present results with multiple time budgets. In fact, the unreliability pattern for the 90-min time budget in Fig. 5 is very consistent with prior findings (Wessel & Farber 2019), which suggests the existence of saturation in those systems; (5) The COTA system is a very geographically large and sparse bus system, and the peak unreliability occurs at a time budget of around 45 min as shown in Fig. 6. In other cities such as Toronto and San Francisco, peak unreliability occurs at a time budget of less than 30 min (Wessel & Farber 2019). This means that it takes users in Columbus much longer to travel to the edge of the system, and the unreliability requires a longer time budget to reach saturation.
4.3 Temporal patterns
We now turn to temporal patterns in schedule-based unreliability. We conducted temporal analysis on several dimensions in terms of the start time: daily, days of week, and hours.
4.3.1 Daily
Figure 7 shows the daily pattern of the normalized accessibility unreliability from 2018 to 2019. Because larger time budgets have less volatile patterns due to saturation, we only include the results for time budgets of five to 60 min. Time budgets larger than 15 min show generally similar and higher-variance patterns, while smaller time budgets have patterns exhibiting lower variance. We observe similar patterns in the spatial analysis (e.g., global average trend in Fig. 6) and other temporal analyses (e.g., hourly pattern). We can observe two spikes among different months: February and September to October. We speculate this may be linked to the seasonal schedule adjustments in January, May, and September every year, as operators need time to adjust to the new schedule leading to higher unreliability.
4.3.2 Days of the week
Figure 8 shows the average normalized schedule-based accessibility unreliability for each day of the week for the week of Sep 4, 2019, at 8am for time budgets ranging from five to 60 min. We selected this week because it is during the most recent four months in the analysis period and has a typical level of unreliability daily analysis in Fig. 7. The pattern shows that Wednesday, Friday, and Tuesday have the highest unreliability, while Monday, Saturday, and Sunday have the lowest unreliability. This pattern is consistent with prior findings about delay (Park et al. 2020) and risk of missing transfers (Liu & Miller 2020b) in the COTA bus system, which shows the inherent connections of accessibility unreliability to delay and transfer time penalty.
4.3.3 Hourly
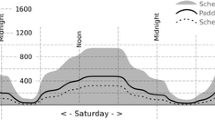
Figure 9 presents the hourly pattern for schedule-based accessibility—i.e., the unreliability on the hour from 6:00 to 23:00 on Sep 4, 2019. We chose the day as a typical day for the same rationale described previously: the daily analysis shows that unreliability on this day is neither too high nor too low. The unreliability varies little throughout the day. The highest unreliability generally occurs during the morning rush hour (8:00) and the afternoon rush hour (18:00), which is also consistent with the hourly pattern of delay (Park et al. 2020) and risk of missing transfers (Liu & Miller 2020b). The hourly variation becomes less obvious for very small time budgets (such as 5 min), which is also consistent with the analysis above.
5 Conclusion
Measuring transit user’s accessibility is a crucial part of public transit research and a prerequisite of transit planning and policy making. Among numerous accessibility measures, the space–time prism (STP) is an especially effective method for measuring the physical accessible area afforded by the system for transit users; as more real-time data become available, the size and fidelity of the analysis can increase correspondingly. However, traditional measures still largely rely on schedule data, which cannot reflect the variation in the transit system’s on-time performance (Wessel et al. 2017; Wessel & Farber 2019). Some prior studies used retrospective real-time methods to calculate accessibility using real-time data; however, these measures assume transit users know future arrival times a priori (Wessel & Farber 2019) and never miss a bus, thus overestimating the ability of users to obtain information and reach destinations. This paper introduces a new time geography approach—realizable real-time space–time prism—to address the limitations of schedule-based and retrospective real-time measures and incorporate transit users’ capabilities in the calculation of accessibility. The realizable STP is novel in that it is a two-step method that accounts for both the decision-making and implementation processes of a user. We, moreover, introduce accessibility unreliability as the normalized difference between schedule-based or retrospective-based measure and the realizable measure. Thus, unreliability quantifies degree to which traditional measures overestimate accessibility. Put another way, unreliability quantifies the difference between a transit system’s expected performance and its realized performance in terms of accessibility.
This paper provides findings that can make accessibility more practical for transit users, planners, and authorities. We use high-resolution real-time General Transit Feed Specification (GTFS) data and a time-dependent routing algorithm to implement the proposed methods for the Central Ohio Transit Authority (COTA) bus system in Columbus, Ohio, USA. Our analyses show that the potential path area of realizable accessibility is always the smallest compared to the other two measures and cannot cover all the COTA system even given a large (two hour) time budget. Therefore, the realizable STP is a different, more conservative measure compared to its scheduled and retrospective counterparts. We also find the global average performance of scheduled and retrospective accessibility are very similar. We then explore the spatial pattern of schedule-based accessibility unreliability and its relationship with time budget. As a function of time budget, high unreliability tends to spread from the city center to the suburban fringe as time budget increases, but is followed by a pattern of low unreliability spreading from the center as time budget continues to increase. This is due to a saturation effect coinciding with very large time budgets that occurs when schedule- or retrospective-based measures reach all the stops possible in a finite system. Our temporal analyses demonstrate that unreliability for schedule-based accessibility is higher in February and September, morning and afternoon rush hours, and the middle of the week. This is consistent with prior findings related to bus delays (Park et al. 2020) and the risk of missing transfers (Liu & Miller 2020b), indicating the inherent connections between these phenomena and unreliability.
The realizable STP can be a more user-centric and conservative measure for future transit planning and operation, and its pattern shows the asymmetric reality of transit planning: many transit systems set a very high standard for transit users and operators (e.g., trips involving two or three transfers with very high uncertainties); however, this expectation cannot be delivered to transit users by operators (e.g., missing buses and wait for the next bus for hours). Meanwhile, if schedule data are used as the sole data source for planning outcome measurement, the unreliability issues may never be addressed during the planning process due to lack of awareness. As transit authorities aim to enhance accessibility from the system’s perspective, it is equally important to consider this from a user’s perspective, i.e., whether a user can complete trips in the real world. This requires greater use of real-time analysis and big data with larger volume and faster velocity during the transit planning process in the future. If planning continues to be based on schedule alone, it is imperative for authorities and planners to consider the inherent unreliability of scheduled and retrospective measures and plan more conservatively.
There are several topics that remain unexplored in this paper. First, our analysis only allows for following the schedule as a user’s trip planning strategy, which cannot be universally applied to every transit user. As real-time information (RTI) becomes more accessible, more advanced real-time prediction algorithms can significantly enhance the experience of a user. Rather than attempting to account for the continuum of possible RTI integration, we provide the retrospective measure as the upper bound (perfect RTI) and the realizable measure as the lower bound (no RTI) for use as benchmarks. Second, despite incorporating users’ cognitive factors in the calculation, the paper’s scope is still within the physical accessibility afforded by the system and there are no behavioral data to, moreover, reaffirm the findings, such as how the measured unreliability impacts actual user’s transit experience or overall ridership. Future studies can survey transit users’ perceived accessibility and compare the results with the three introduced measures to investigate the impact of unreliability on the demand side. Third, this paper is based on a rigorous, time-dependent Dijkstra routing algorithm, and results based on this algorithm may differ from other mainstream routing algorithms (e.g., Open Trip Planner) which likely use heuristics for scalability. However, although each algorithm can have its own specific implementation, it is indeed a universal risk of retrospective-based algorithms to make the overestimation mistakes discussed in this paper. Last, the empirical results derived from the COTA system may not be able to be applied to other systems; we hope future studies can conduct similar analysis on other transit systems and explore the relationship between unreliability and different aspects of system network topology, such as route alignment, stop locations, and headways.
References
Ahn B-H, Shin J-Y (1991) Vehicle-routeing with time windows and time-varying congestion. J Oper Res Soc 42(5):393–400
Arbex R, Cunha CB (2020) Estimating the influence of crowding and travel time variability on accessibility to jobs in a large public transport network using smart card big data. J Transp Geogr 85:102671
Banister D (2008) The sustainable mobility paradigm. Transp Policy 15(2):73–80
Barbeau SJ, Antrim A (2013) The many uses of GTFS data–opening the door to transit and multimodal applications. In: ITS America 2013. Nashville, Tennessee: Intelligent Transportation Society of America. http://prezi.com/-69luw8sfabp/the-many-uses-of-gtfs-data-its-america-april-2013/ Accessed
Batty M (2013) Big data, smart cities and city planning. Dialog Human Geogr 3(3):274–279
Boisjoly G, El-Geneidy AM (2017) How to get there? a critical assessment of accessibility objectives and indicators in metropolitan transportation plans. Transp Policy 55:38–50
Burns LD (1980) Transportation, temporal, and spatial components of accessibility
Central Ohio Transit Authority (2021) Data. https://www.cota.com/data/ Accessed 27 Jun 2021
Chen BY, Li Q, Wang D, Shaw S-L, Lam WHK, Yuan H, Fang Z (2013) Reliable space–time prisms under travel time uncertainty. Ann Assoc Am Geogr 103(6):1502–1521
Chen BY, Yuan H, Li Q, Shaw S-L, Lam WHK, Chen X (2016) Spatiotemporal data model for network time geographic analysis in the era of big data. Int J Geogr Inf Sci 30(6):1041–1071
Conway MW, Byrd A, van Eggermond M (2018) Accounting for uncertainty and variation in accessibility metrics for public transport sketch planning. J Transp Land Use 11(1):541–558
Delafontaine M, Neutens T, Van de Weghe N (2011) Modelling potential movement in constrained travel environments using rough space–time prisms. Int J Geogr Inf Sci 25(9):1389–1411
Google Developers (2020) GTFS static overview | static transit | google developers. https://developers.google.com/transit/gtfs/ Accessed 26 May 2021
Fang Z, Shaw S-L, Tu W, Li Q, Li Y (2012) Spatiotemporal analysis of critical transportation links based on time geographic concepts: a case study of critical bridges in Wuhan, China. J Transp Geogr 23:44–59
Farber S, Bartholomew K, Li X, Páez A, Habib KMN (2014) Assessing social equity in distance based transit fares using a model of travel behavior. Transp Res Part a: Policy Pract 67:291–303
Farber S, O’Kelly M, Miller HJ, Neutens T (2015) Measuring segregation using patterns of daily travel behavior: a social interaction based model of exposure. J Transp Geogr 49:26–38
Gendreau M, Ghiani G, Guerriero E (2015) Time-dependent routing problems: a review. Comput Oper Res 64:189–197
Golden B (1976) Shortest-path algorithms: a comparison. Oper Res 24(6):1164–1168
Google (2021) GTFS realtime overview. https://developers.google.com/transit/gtfs-realtime Accessed 27 Jun 2021
Hägerstrand T (1970) What about people in regional science. Pap Reg Sci Assoc 24:6–21
Hall RW (1983) Travel outcome and performance: the effect of uncertainty on accessibility. Transp Res Part b: Methodol 17(4):275–290
Handy S (2020) Is accessibility an idea whose time has finally come? Transp Res Part d: Transp Environ 83:102319
Hansen WG (1959) How accessibility shapes land use. J Am Inst Plann 25(2):73–76
Hsiao S, Lu J, Sterling J, Weatherford M (1997) Use of geographic information system for analysis of transit pedestrian access. Transp Res Rec 1604(1):50–59
Ichoua S, Gendreau M, Potvin J-Y (2003) Vehicle dispatching with time-dependent travel times. Eur J Oper Res 144(2):379–396
Ingram DR (1971) The concept of accessibility: a search for an operational form. Reg Stud 5(2):101–107
Kim H, Song Y (2018) An integrated measure of accessibility and reliability of mass transit systems. Transportation 45(4):1075–1100
Lee J, Miller HJ (2018) Measuring the impacts of new public transit services on space-time accessibility: an analysis of transit system redesign and new bus rapid transit in Columbus, Ohio, USA. Appl Geogr 93:47–63. https://doi.org/10.1016/j.apgeog.2018.02.012
Lenntorp B (1976) Paths in space-time environments: a time-geographic sudy of movement possibilities of individuals. Lund Stud Geogr B 44:150p
Levinson D, Wu H (2020) Towards a general theory of access. J Transp Land Use 13(1):129–158
Li X, Farber S (2016) Spatial representation in the social interaction potential metric: an analysis of scale and parameter sensitivity. J Geogr Syst 18(4):331–357
Li Q, Zhang T, Wang H, Zeng Z (2011) Dynamic accessibility mapping using floating car data: a network-constrained density estimation approach. J Transp Geogr 19(3):379–393
Liu L, Miller HJ (2020a) Does real-time transit information reduce waiting time? an empirical analysis. Transp Res Part a: Policy Pract 141:167–179
Liu L, Miller HJ (2020b) Measuring risk of missing transfers in public transit systems using high-resolution schedule and real-time bus location data. Urb Stud. https://doi.org/10.1177/0042098020919323
Liu L, Miller HJ, Scheff J (2020) The impacts of COVID-19 pandemic on public transit demand in the United States. PLoS ONE 15(11):e0242476. https://doi.org/10.1371/journal.pone.0242476
Malekzadeh A, Chung E (2020) A review of transit accessibility models: challenges in developing transit accessibility models. Int J Sustain Transp 14(10):733–748
Miller HJ (1991) Modelling accessibility using space-time prism concepts within geographical information systems. Int J Geogr Inf Syst 5(3):287–301
Miller HJ (1999) Measuring space-time accessibility benefits within transportation networks: basic theory and computational procedures. Geogr Anal 31(1):187–212
Miller HJ (2017) Time geography and space-time prism. In: International encyclopedia of geography: people, the earth, environment and technology, (pp 1–19)
Mohadisdudis HM, Ali NM (2014) A study of smartphone usage and barriers among the elderly. In: 2014 3rd International conference on user science and engineering (i-USEr) IEEE, pp 109–114
Neutens T, Witlox F, Demaeyer P (2007) Individual accessibility and travel possibilities: a literature review on time geography. Eur J Transp Infrastruct Res, 7(4)
O’Sullivan D, Morrison A, Shearer J (2000) Using desktop GIS for the investigation of accessibility by public transport: an isochrone approach. Int J Geogr Inf Sci 14(1):85–104
Owen A, Levinson DM (2015) Modeling the commute mode share of transit using continuous accessibility to jobs. Transp Res Part a: Policy Pract 74:110–122
Park Y, Mount J, Liu L, Xiao N, Miller HJ (2020) Assessing public transit performance using real-time data: spatiotemporal patterns of bus operation delays in Columbus, Ohio, USA. Int J Geogr Inf Sci 34(2):367–392. https://doi.org/10.1080/13658816.2019.1608997
Pereira RHM, Saraiva M, Herszenhut D, Braga CKV, Conway MW (2021) r5r: rapid realistic routing on multimodal transport networks with r 5 in r. Findings. https://doi.org/10.32866/001c.21262
Ryan J, Pereira RHM (2021) What are we missing when we measure accessibility? comparing calculated and self-reported accounts among older people. J Transp Geogr 93:103086
Schmitt A (2018) The Columbus bus network redesign boosted ridership. https://usa.streetsblog.org/2018/08/14/the-columbus-bus-network-redesign-boosted-ridership/ Accessed 29 Jun 2021
Tasic I, Zhou X, Zlatkovic M (2014) Use of spatiotemporal constraints to quantify transit accessibility: case study of potential transit-oriented development in West Valley City Utah. Transp Res Rec 2417(1):130–138
Tribby CP, Zandbergen PA (2012) High-resolution spatio-temporal modeling of public transit accessibility. Appl Geogr 34:345–355
Tsetsi E, Rains SA (2017) Smartphone Internet access and use: extending the digital divide and usage gap. Mob Med Commun 5(3):239–255
Wang Y, Yuan Y, Ma Y, Wang G (2019) Time-dependent graphs: definitions, applications, and algorithms. Data Sci Eng 4(4):352–366
Wessel N, Farber S (2019) On the accuracy of schedule-based GTFS for measuring accessibility. J Transp Land Use 12(1):475–500
Wessel N, Allen J, Farber S (2017) Constructing a routable retrospective transit timetable from a real-time vehicle location feed and GTFS. J Transp Geogr 62:92–97
Widener MJ, Farber S, Neutens T, Horner M (2015) Spatiotemporal accessibility to supermarkets using public transit: an interaction potential approach in Cincinnati, Ohio. J Transp Geogr 42:72–83
Wu H, Levinson D (2020) Unifying access. Transp Res Part d: Transp Environ 83:102355
Wu Y-H, Miller HJ (2001) Computational tools for measuring space-time accessibility within dynamic flow transportation networks. J Transp Stat 4(2/3):1–14
Xie D, Zhu H, Yan L, Yuan S, Zhang J (2012) An improved Dijkstra algorithm in GIS application. In: World automation congress 2012 IEEE, pp 167–169
Zhang T, Dong S, Zeng Z, Li J (2018) Quantifying multi-modal public transit accessibility for large metropolitan areas: a time-dependent reliability modeling approach. Int J Geogr Inf Sci 32(8):1649–1676
Zhao F, Chow L-F, Li M-T, Ubaka I, Gan A (2003) Forecasting transit walk accessibility: regression model alternative to buffer method. Transp Res Rec 1835(1):34–41
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
All scripts used in the paper can be found in this GitHub repository: https://github.com/luyuliu/Realizable-Accessibility.
Rights and permissions
About this article
Cite this article
Liu, L., Porr, A. & Miller, H.J. Realizable accessibility: evaluating the reliability of public transit accessibility using high-resolution real-time data. J Geogr Syst 25, 429–451 (2023). https://doi.org/10.1007/s10109-022-00382-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10109-022-00382-w
Keywords
- Accessibility unreliability
- GTFS
- Space–time prism
- Schedule-based accessibility
- Retrospective real-time accessibility
- Realizable real-time accessibility