Skip to main content

Advertisement

SpringerLink
Log in

Lagrange multipliers, (exact) regularization and error bounds for monotone variational inequalities

  • Full Length Paper
  • Series A
  • Published:
Mathematical Programming Submit manuscript

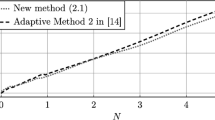
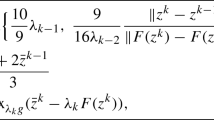Abstract

We examine two central regularization strategies for monotone variational inequalities, the first a direct regularization of the operative monotone mapping, and the second via regularization of the associated dual gap function. A key link in the relationship between the solution sets to these various regularized problems is the idea of exact regularization, which, in turn, is fundamentally associated with the existence of Lagrange multipliers for the regularized variational inequality. A regularization is said to be exact if a solution to the regularized problem is a solution to the unregularized problem for all parameters beyond a certain value. The Lagrange multipliers corresponding to a particular regularization of a variational inequality, on the other hand, are defined via the dual gap function. Our analysis suggests various conceptual, iteratively regularized numerical schemes, for which we provide error bounds, and hence stopping criteria, under the additional assumption that the solution set to the unregularized problem is what we call weakly sharp of order greater than one.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Auslender, A.: Resolution numerique d’inegalities variationanelles. Acad. Sci. Paris. Ser. A-B 276, 1063–1066 (1973)

    MATH  MathSciNet  Google Scholar 

  2. Aussel, D., Dutta, J.: On gap functions for multivalued Stampacchia variational Inequalities. J. Optim. Theory Appl. 149(3), 513–527 (2011)

    Article  MATH  MathSciNet  Google Scholar 

  3. Bank, B., Guddat, J., Klatte, D., Kummer, B., Tammer, K.: Non-linear Parametric Optimization. Birkhuser Verlag, Basel (1983)

    MATH  Google Scholar 

  4. Burke, J.V., Ferris, M.C.: Weak sharp minima in mathematical programming. SIAM J. Control. Optim. 31, 1340–1359 (1993)

    Article  MATH  MathSciNet  Google Scholar 

  5. Clarke, F.H.: Optimization and Nonsmooth Analysis. Wiley, New York (1983)

    MATH  Google Scholar 

  6. Dutta, J.: Gap functons and errorbounds for variational and generalized variational inequalities. Vietnam J. Math. 40, 231–253 (2012)

    MathSciNet  Google Scholar 

  7. Facchinei, F., Pang, J.S., Lampariello, L.: VI-constrained hemivariational inequalities: distributed algorithms and power control in ad-hoc networks. Math. Program. A 145(1–2), 59–96 (2014)

    Article  MATH  MathSciNet  Google Scholar 

  8. Facchinei, F., Kanzow, C.: Beyond monotonicity in regularization methods for nonlinear complimentarity problems. SIAM J. Control. Optim. 37(4), 1150–1162 (1999)

    Article  MATH  Google Scholar 

  9. Facchinei, F., Pang, J.S.: Finite-Dimensional Variational Inequalities and Complementarity Problems, Volume I and II. Springer, New York (2003)

    MATH  Google Scholar 

  10. Friedlander, M.P., Tseng, P.: Exact regularization of convex programs. SIAM J. Optim. 18, 1326–1350 (2007)

    Article  MATH  MathSciNet  Google Scholar 

  11. Fukushima, M.: Equivalent differentiable optimization problems and descent methods for asymmetric variational inequality problems. Math. Prog. A 53(1), 99–110 (1992)

    Article  MATH  MathSciNet  Google Scholar 

  12. Li, G., Ng, K.F.: Error bounds of generalized D-gap functions for nonsmooth and nonmonotone variational inequality problems. SIAM J. Optim 20(No. 2), 667–690 (1998)

    Article  MATH  MathSciNet  Google Scholar 

  13. Marcotte, P., Zhu, D.: Weak sharp solutions of variational inequalities. SIAM J. Optim 9(No. 1), 179–189 (1998)

    Article  MATH  MathSciNet  Google Scholar 

  14. Peng, J.M.: Equivalence of variational inequality problems to unconstrained minimization. Math. Program. A 78, 347–355 (1997)

    MATH  MathSciNet  Google Scholar 

  15. Rockafellar, R.T.: Convex Analysis. Princeton University Press, Princeton, NJ (2005)

    MATH  Google Scholar 

  16. Rockafellar, R.T., Wets, R.J.-B.: Variational Analysis, 3rd edn. Springer, Berlin (2009)

    MATH  Google Scholar 

  17. Yamashita, N., Taji, K., Fukushima, M.: Unconstrained optimization reformulations of variational inequality problems. J. Optim. Theory Appl. 92, 439–456 (1997)

    Article  MATH  MathSciNet  Google Scholar 

Download references

Acknowledgments

The research of CC and DRL was supported by the Deutsche Forschungsgemeinschaft/German Research Foundation Grant SFB755-A4 and SFB755-C2.

Author information

Authors and Affiliations

  1. Institut für Numerische und Angewandte Mathematik, Universität Göttingen, 37083, Göttingen, Germany

    C. Charitha

  2. Economics Group, Department of Humanities and Social Sciences, Indian Institute of Technology Kanpur, Kanpur, 208016, India

    Joydeep Dutta

  3. Institut für Numerische und Angewandte Mathematik, Universität Göttingen, 37083, Göttingen, Germany

    D. Russell Luke

Authors
  1. C. Charitha
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Joydeep Dutta
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. D. Russell Luke
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to D. Russell Luke.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Charitha, C., Dutta, J. & Luke, D.R. Lagrange multipliers, (exact) regularization and error bounds for monotone variational inequalities. Math. Program. 161, 519–549 (2017). https://doi.org/10.1007/s10107-016-1022-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10107-016-1022-6

Keywords

Mathematics Subject Classification

Search

Navigation