Abstract.
The maximum integer skew-symmetric flow problem (MSFP) generalizes both the maximum flow and maximum matching problems. It was introduced by Tutte [28] in terms of self-conjugate flows in antisymmetrical digraphs. He showed that for these objects there are natural analogs of classical theoretical results on usual network flows, such as the flow decomposition, augmenting path, and max-flow min-cut theorems. We give unified and shorter proofs for those theoretical results. We then extend to MSFP the shortest augmenting path method of Edmonds and Karp [7] and the blocking flow method of Dinits [4], obtaining algorithms with similar time bounds in general case. Moreover, in the cases of unit arc capacities and unit “node capacities” our blocking skew-symmetric flow algorithm has time bounds similar to those established in [8, 21] for Dinits’ algorithm. In particular, this implies an algorithm for finding a maximum matching in a nonbipartite graph in  time, which matches the time bound for the algorithm of Micali and Vazirani [25]. Finally, extending a clique compression technique of Feder and Motwani [9] to particular skew-symmetric graphs, we speed up the implied maximum matching algorithm to run in
time, which matches the time bound for the algorithm of Micali and Vazirani [25]. Finally, extending a clique compression technique of Feder and Motwani [9] to particular skew-symmetric graphs, we speed up the implied maximum matching algorithm to run in  time, improving the best known bound for dense nonbipartite graphs. Also other theoretical and algorithmic results on skew-symmetric flows and their applications are presented.
time, improving the best known bound for dense nonbipartite graphs. Also other theoretical and algorithmic results on skew-symmetric flows and their applications are presented.
Similar content being viewed by others
References
Anstee, R.P.: An algorithmic proof of Tuttes’ f-factor theorem. J. of Algorithms 6, 112–131 (1985)
Anstee, R.P.: A polynomial algorithm for b-matchings: An alternative approach. Information Proc. Letters 24, 153–157 (1987)
Blum, N.: A new approach to maximum matching in general graphs. In Automata, Languages and Programming [Lecture Notes in Comput. Sci. 443] (Springer, Berlin, 1990), pp. 586–597
Dinic, E. A.: Algorithm for solution of a problem of maximum flow in networks with power estimation. Soviet Math. Dokl. 11, 1277–1280 (1970)
Edmonds, J.: Paths, trees and flowers. Canadian J. Math. 17, 449–467 (1965)
Edmonds, J., Johnson, E. L.: Matching: a well-solved class of integer linear programs. In R. Guy, H. Haneni, and J. Schönheim, eds, Combinatorial Structures and Their Applications, Gordon and Breach, NY, 1970, pp. 89–92
Edmonds, J., Karp, R. M.: Theoretical improvements in algorithmic efficiency for network flow problems. J. Assoc. Comput. Mach. 19, 248–264 (1972)
Even, S., Tarjan, R. E.: Network flow and testing graph connectivity. SIAM J. Comput. 4, 507–518 (1975)
Feder, T., Motwani, R.: Clique partitions, graph compression and speeding-up algorithms. In Proc. 23rd Annual ACM Symp. on Theory of Computing, 1991, pp. 123–133
Ford, L. R., Fulkerson, D. R.: Flows in Networks. Princeton Univ. Press, Princeton, NJ, 1962
Fremuth-Paeger, C., Jungnickel, D.: Balanced network flows. Parts I–III. Networks 33, 1–56 (1999)
Gabow, H. N.: An efficient reduction technique for degree-constrained subgraph and bidirected network flow problems. Proc. of STOC 15, 448–456 (1983)
Gabow, H. N., Tarjan, R. E.: A linear-time algorithm for a special case of disjoint set union. J. Comp. and Syst. Sci. 30, 209–221 (1985)
Gabow, H. N., Tarjan, R. E.: Faster scaling algorithms for general graph-matching problems. J. ACM 38, 815–853 (1991)
Goldberg, A. V., Karzanov, A. V.: Maximum skew-symmetric flows. In P. Spirakis, ed., Algorithms – ESA ‘95 (Proc. 3rd European Symp. on Algorithms). Lecture Notes in Computer Sci. 979, 155–170 (1995)
Goldberg, A. V., Karzanov, A. V.: Path problems in skew-symmetric graphs. Combinatorica 16, 129–174 (1996)
Goldberg, A. V., Karzanov, A. V.: Maximum skew-symmetric flows and their applications to b-matchings. Preprint 99-043, SFB 343, Bielefeld Universität, Bielefeld, April 1999, 25 pp
Hopcroft, J. E., Karp, R. M.: An n5/2 algorithm for maximum matching in bipartite graphs. SIAM J. Comput. 2, 225–231 (1973)
Karzanov, A. V.: Èkonomnyi algoritm nakhozhdeniya bikomponent grafa [Russian; An efficient algorithm for finding the bicomponents of a graph]. In Trudy Tret’ei Zimnei Shkoly po Matematicheskomu Programmirovaniyu i Smezhnym Voprosam [Proc. of 3rd Winter School on Mathematical Programming and Related Topics], issue 2. Moscow Engineering and Construction Inst. Press, Moscow, 1970, pp. 343–347
Karzanov, A.V.: Tochnaya otsenka algoritma nakhozhdeniya maksimal’nogo potoka, primenennogo k zadache ‘‘o predstavitelyakh’’ [Russian; An exact estimate of an algorithm for finding a maximum flow, applied to the problem ‘‘of representatives’’]. In Voprosy Kibernetiki [Problems of Cybernetics], volume~3. Sovetskoe Radio, Moscow, 1973, pp. 66–70
Karzanov, A.V.: O nakhozhdenii maksimal’nogo potoka v setyakh spetsial’nogo vida i nekotorykh prilozheniyakh [Russian; On finding maximum flows in networks with special structure and some applications]. In Matematicheskie Voprosy Upravleniya Proizvodstvom [Mathematical Problems for Production Control], volume~5. Moscow State University Press, Moscow, 1973, pp. 81–94
Kocay, W., Stone, D.: Balanced network flows. Bulletin of the ICA 7, 17–32 (1993)
Lawler, E. L.: Combinatorial Optimization: Networks and Matroids. Holt, Reinhart, and Winston, New York, NY., 1976
Lovász, L., Plummer, M. D.: Matching Theory. Akadémiai Kiadó, Budapest, 1986
Micali, S., Vazirani, V.V.: An
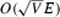 algorithm for finding maximum matching in general graphs. Proc. of the 21st Annual IEEE Symposium in Foundation of Computer Science, 1980, pp. 71–109
algorithm for finding maximum matching in general graphs. Proc. of the 21st Annual IEEE Symposium in Foundation of Computer Science, 1980, pp. 71–109Schrijver, A.: Combinatorial Optimization. Polyhedra and Efficiency, Volume~A. (Algorithms and Combinatorics 24), Springer, Berlin and etc., 2003
Tarjan, R.: Depth-first search and linear graph algorithms. SIAM J. Comput. 1, 146–160 (1972)
Tutte, W.T.: Antisymmetrical digraphs. Canadian J. Math. 19, 1101–1117 (1967)
Vazirani, V.V.: A theory of alternating paths and blossoms for proving correctness of the
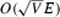 general graph maximum matching algorithm. In: R. Kannan and W.R. Cunningham, eds., Integer Programming and Combinatorial Optimization (Proc. 1st IPCO Conference), University of Waterloo Press, Waterloo, Ontario, 1990, pp. 509–535
general graph maximum matching algorithm. In: R. Kannan and W.R. Cunningham, eds., Integer Programming and Combinatorial Optimization (Proc. 1st IPCO Conference), University of Waterloo Press, Waterloo, Ontario, 1990, pp. 509–535
Author information
Authors and Affiliations
Corresponding author
Additional information
Mathematics Subject Classification (1991): 90C27, 90B10, 90C10, 05C85
Rights and permissions
About this article
Cite this article
Goldberg, A., Karzanov, A. Maximum skew-symmetric flows and matchings. Math. Program., Ser. A 100, 537–568 (2004). https://doi.org/10.1007/s10107-004-0505-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10107-004-0505-z





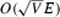 algorithm for finding maximum matching in general graphs. Proc. of the 21st Annual IEEE Symposium in Foundation of Computer Science, 1980, pp. 71–109
algorithm for finding maximum matching in general graphs. Proc. of the 21st Annual IEEE Symposium in Foundation of Computer Science, 1980, pp. 71–109