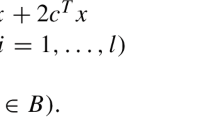Abstract.
Let  where
where  and
and  i is an n×n positive semidefinite matrix. We prove that the volumetric and combined volumetric-logarithmic barriers for
i is an n×n positive semidefinite matrix. We prove that the volumetric and combined volumetric-logarithmic barriers for  are
are  and
and  self-concordant, respectively. Our analysis uses the semidefinite programming (SDP) representation for the convex quadratic constraints defining
self-concordant, respectively. Our analysis uses the semidefinite programming (SDP) representation for the convex quadratic constraints defining  , and our earlier results on the volumetric barrier for SDP. The self-concordance results actually hold for a class of SDP problems more general than those corresponding to the SDP representation of
, and our earlier results on the volumetric barrier for SDP. The self-concordance results actually hold for a class of SDP problems more general than those corresponding to the SDP representation of  .
.
Similar content being viewed by others
References
Alizadeh, F.: Interior point methods in semidefinite programming with applications to combinatorial optimization. SIAM J. Optim. 5, 13–51 (1995)
Anstreicher, K.M.: Large step volumetric potential reduction algorithms for linear programming. Ann. Oper. Res. 62, 521–538 (1996)
Anstreicher, K.M.: Volumetric path following algorithms for linear programming. Math. Program. 76, 245–263 (1997)
Anstreicher, K.M.: On Vaidya’s volumetric cutting plane method for convex programming. Math. Oper. Res. 22, 63–89 (1997)
Anstreicher, K.M.: The volumetric barrier for semidefinite programming. Math. Oper. Res. 25, 365–380 (2000)
Güler, O., Tunçel, L.: Characterization of the barrier parameter of homogeneous convex cones. Math. Program. 81, 55–76 (1998)
Horn, R.A., Johnson, C.R.: Matrix Analysis. Cambridge University Press, Cambridge, 1985
Nesterov, N., Nemirovskii, A.: Interior-Point Polynomial Algorithms in Convex Programming. SIAM, Philadelphia, 1994
Vaidya, P.M.: A new algorithm for minimizing convex functions over convex sets. Math. Program. 73, 291–341 (1996)
Vaidya, P.M., Atkinson, D.S.: A technique for bounding the number of iterations in path following algorithms. In: Complexity in Numerical Optimization, Pardalos, P.M., (ed.), World Scientific, Singapore, 1993, pp. 462–489
Vandenberghe, L., Boyd, S.: Semidefinite programming. SIAM Rev. 38, 49–95 (1996)
Author information
Authors and Affiliations
Corresponding author
Additional information
Mathematics Subject Classification (1991):90C25, 90C30
Rights and permissions
About this article
Cite this article
Anstreicher, K. The volumetric barrier for convex quadratic constraints. Math. Program., Ser. A 100, 613–662 (2004). https://doi.org/10.1007/s10107-003-0513-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10107-003-0513-4