Abstract
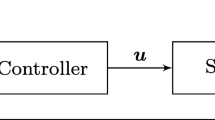
Decentralized scheduling with dispatching rules is applied in many fields of logistics and production, especially in highly complex and dynamic scenarios, such as semiconductor manufacturing. Many dispatching rules are proposed in the literature, which perform well on specific scenarios. No rule is known, however, consistently outperforming all other rules. One approach to meet this challenge and improve scheduling performance is to select and switch dispatching rules depending on current system conditions. For this task machine learning techniques (e.g., Artificial Neural Networks) are frequently used. In this paper we investigate the use of a machine learning technique not applied to this task before: Gaussian process regression. Our analysis shows that Gaussian processes predict dispatching rule performance better than Neural Networks in most settings. Additionally, already a single Gaussian Process model can easily provide a measure of prediction quality. This is in contrast to many other machine learning techniques. We show how to use this measure to dynamically add additional training data and incrementally improve the model where necessary. Results therefore suggest, Gaussian processes are a very promising technique, which can lead to better scheduling performance (e.g., reduced mean tardiness) compared to other techniques.





Similar content being viewed by others
References
Alpaydin E (2004) Introduction to machine learning (adaptive computation and machine learning series), vol 14. The MIT Press, Cambridge
Becker T, Windt K (2011) A comparative view on existing autonomous control approaches: observations from a simulation study. In: Hülsmann M, Scholz-Reiter B, Windt K (eds) Autonomous cooperation and control in logistics. Springer Berlin Heidelberg, pp 275–289
Blackstone JH, Phillips DT, Hogg GL (1982) A state-of-the-art survey of dispatching rules for manufacturing job shop operations. Int J Prod Res 20(1):27–45
Conway RW (1965) Priority dispatching and job lateness in a job shop. J Ind Eng 16:228–237
Dashkovskiy S, Karimi HR, Kosmykov M (2012) A Lyapunov-Razumikhin approach for stability analysis of logistics networks with time-delays. Int J Syst Sci 43(5):845–853
El-Bouri A, Shah P (2006) A neural network for dispatching rule selection in a job shop. Int J Adv Manuf Technol 31(3–4):342–349
Guneri AF, Gumus AT (2008) Artificial neural networks for finite capacity scheduling: a comparative study. Int J Ind Eng 15(4):349–359
Hall M, Frank E, Holmes G, Pfahringer B, Reutemann P, Witten H (2009) The weka data mining software: an update. SIGKDD Explor Newsl 11(1):10–18
Hvalica D (2012) Solving job shop problems in the context of hypergraphs. Central Eur J Oper Res 21(1): 1–14. doi:10.1007/s10100-012-0268-1
Haupt R (1989) A survey of priority rule-based scheduling. Oper Res Spektrum 11(1):3–16
Heger J, Hildebrandt T, Scholz-Reiter B (2013) Switching dispatching rules with Gaussian processes. In: Windt K (ed) Lecture notes in production engineering: Robust manufacturing control. Springer, Berlin
Hentsch K, Köchel P (2011) Job scheduling with forbidden setups and two objectives using genetic algorithms and penalties. Central Eur J Oper Res 19:285–298
Hildebrandt T, Heger J, Scholz-Reiter B (2010) Towards improved dispatching rules for complex shop floor scenarios: a genetic programming approach. In: Proceedings of the 12th annual conference on genetic and evolutionary computation, Portland, USA, pp 257–264
Holthaus O, Rajendran C (1997) Efficient dispatching rules for scheduling in a job shop. Int J Prod Econ 48(1):87–105
Holthaus O, Rajendran C (2000) Efficient jobshop dispatching rules: further developments. Prod Plan Control 11(2):171–178
Huffman BJ (2001) An object-oriented version of SIMLIB (a simple simulation package). INFORMS Trans Educ 2(1):1–15
Karimi HR, Duffie NA, Dashkovskiy S (2010) Local capacity H\_infinity control for production networks of autonomous work systems with time-varying delays. IEEE Trans Autom Sci Eng 7(4):849–857
Kotsiantis SB (2007) Supervised machine learning: a review of classification techniques. Informatica 31:249–268
Law AM (2007) Simulation modeling and analysis, 4th edn. McGraw-Hill, Boston
MacKay DJC (1998) Introduction to Gaussian processes. In: Bishop CM (ed) Neural networks and machine learning, NATO ASI series, vol 168. Springer, Berlin, pp 133–165
Mouelhi-Chibani W, Pierreval H (2010) Training a neural network to select dispatching rules in real time. Comput Ind Eng 58(2):249–256. Scheduling in Healthcare and Industrial Systems
Neal RM (1996) Bayesian learning for neural networks (Lecture Notes in Statistics), 1st edn. Springer, Berlin
O’Hagan A (1978) Curve fitting and optimal design. J R Stat Soc 40(1):1–42
Paciorek CJ, Schervish MJ (2004) Nonstationary covariance functions for gaussian process regression. In: Proceedings of the conference on neural information processing systems (NIPS). MIT Press
Panwalkar SS, Iskander W (1977) A survey of scheduling rules. Oper Res 25(1):45–61
Plagemann C, Kersting K, Burgard W (2008) Nonstationary Gaussian process regression using point estimates of local smoothness. In: Daelemans W, Goethals B, Morik K (eds) Machine learning and knowledge discovery in databases, vol 5212. Springer Berlin Heidelberg, pp 204–219
Priore P, de la Fuente D, Gomez A, Puente J (2001) A review of machine learning in dynamic scheduling of flexible manufacturing systems. AI EDAM 15(03):251–263
Rajendran C, Holthaus O (1999) A comparative study of dispatching rules in dynamic flowshops and jobshops. Eur J Oper Res 116(1):156–170
Rasmussen CE, Williams CKI (2006) Gaussian processes for machine learning (adaptive computation and machine learning). The MIT Press, Cambridge
Rasmussen CE (1996) Evaluation of Gaussian processes and other methods for non-linear regression. PhD thesis, Department of Computer Science, University of Toronto
Sun YL, Yih Y (1996) An intelligent controller for manufacturing cells. Int J Prod Res 34(8):2353–2373
Wilbrecht JK, Prescott WB (1969) The influence of setup time on job shop performance. Manag Sci 16(4):274–280
Williams C (2006) Gaussian processes for machine learning—software examples. http://www.gaussianprocess.org/gpml/code/matlab/doc/
Williams CKI, Rasmussen CE (1996) Gaussian processes for regression. Adv Neural Inf Process Syst 8:514–520
Wu S-YD, Wysk RA (1989) An application of discrete-event simulation to on-line control and scheduling in flexible manufacturing. Int J Prod Res 27(9):1603–1623
Acknowledgments
The authors are grateful to the generous support by the German Research Foundation (DFG) under grant SCHO 540/17-2.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Heger, J., Hildebrandt, T. & Scholz-Reiter, B. Dispatching rule selection with Gaussian processes. Cent Eur J Oper Res 23, 235–249 (2015). https://doi.org/10.1007/s10100-013-0322-7
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10100-013-0322-7