A new stable numerical method for Mellin integral equations in weighted spaces with uniform norm

Abstract

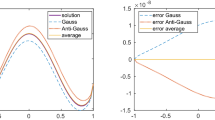
In this paper a new modified Nyström method is proposed to solve linear integral equations of the second kind with fixed singularities of Mellin convolution type. It is based on the Gauss–Radau quadrature formula with a suitable Jacobi weight. The stability and convergence of the method is proved in weighted spaces with uniform norm. Moreover, an error estimate of the numerical solution is given under certain assumptions on the Mellin kernel. The efficiency of the method is shown through some examples. The numerical results also confirm that the error estimate is sharp.

Appendix

In this section we will give some estimates for the quadrature error of the Gauss–Radau formula with respect to a Jacobi weight $v^{\alpha ,\beta }(x)$, $\alpha ,\beta >-1$,

$$\begin{aligned} \int _0^1 F(x)v^{\alpha ,\beta }(x)dx=\sum _{i=1}^n\lambda _{n,i}F(x_{n,i})+e_n(F). \end{aligned}$$

(41)

Now, we recall some useful notation and definitions.

For a function $F \in C$, by $E_n(F)_{\infty }$ we denote the error of best polynomial approximation

$$\begin{aligned} E_n(F)_{\infty }=\inf _{P_n \in \mathbb {P}_n}\Vert F-P_n\Vert _{\infty }, \end{aligned}$$

where $\mathbb {P}_n$ is the set of all algebraic polynomials on [0, 1] of degree at most n.

Taking into account that the algebraic degree of exactness of the formula (41) is $2n-2$, by classical arguments (see, for instance, [12, Theorem 5.1.6]) it can be proved the following

Theorem 8

For any $F \in C$, the estimate

$$\begin{aligned} |e_n(F)| \le 2 \left( \int _0^1 v^{\alpha ,\beta }(x)\,dx\right) E_{2n-2}(F)_{\infty } \end{aligned}$$

(42)

holds true.

For a general weight function w(x) on [0, 1] and $1\le p<+\infty$, we denote by $L^p_{w}$, the weighted space of all real-valued measurable functions F on [0, 1] such that

$$\begin{aligned} \Vert F\Vert _{L^p_{w}}=\Vert w F\Vert _p=\left( \int _{0}^1 |w(x) F(x)|^pdx\right) ^\frac{1}{p}<+\infty . \end{aligned}$$

Moreover, we consider the following weighted Sobolev type subspaces of $L^p_{w}$

$$\begin{aligned} W_r^p(w)=\left\{ F \in L^p_{w} : \ F^{(r-1)}\in AC(0,1), \ \Vert w F^{(r)}\varphi ^r\Vert _p<+\infty \right\} , \end{aligned}$$

where r is a positive integer, $\varphi (x)=\sqrt{x(1-x)}$ and AC(0, 1) denotes the collection of all functions which are absolutely continuous on every closed subset of (0, 1), endowed with the norm

$$\begin{aligned} \Vert F\Vert _{W_r^p(w)}=\Vert w F\Vert _p+\Vert w F^{(r)}\varphi ^r\Vert _p. \end{aligned}$$

Let us denote by

$$\begin{aligned} E_n(F)_{w,p}=\inf _{P\in \mathbb {P}_n}\Vert w (F-P)\Vert _p \end{aligned}$$

the error of weighted best approximation of the function $F\in L^p_{w}$ by means of polynomials of degree at most n. For functions F belonging to $W_r^p(w)$, the following Favard inequality

$$\begin{aligned} E_n(F)_{w,p}\le \frac{{{\mathcal {C}}}}{n}E_{n-1}(F')_{\varphi w,p}, \end{aligned}$$

(43)

holds true for a constant ${{\mathcal {C}}}\ne {{\mathcal {C}}}(n,F)$ (see, for example, [12, (2.5.22), p. 172]). Iterating this inequality, one gets the estimate

$$\begin{aligned} E_n(F)_{w,p}\le \frac{{{\mathcal {C}}}}{n^r} E_{n-r}(F^{(r)})_{\varphi ^r w,p}. \end{aligned}$$

We need the following auxiliary result.

Lemma 3

The knots and weights of the quadrature formula (41) satisfy the following conditions

$$\begin{aligned} \lambda _{n,i} \sim \left\{ \begin{array}{ll} \displaystyle \varDelta x_{n,i} \, v^{\alpha ,\beta }(x_{n,i}), &{} \quad i=2,\ldots ,n-1 \\ \displaystyle \varDelta x_{n,i-1} \, v^{\alpha ,\beta }(x_{n,i}), &{} \quad i=n \end{array} \right. \end{aligned}$$

and

$$\begin{aligned} \lambda _{n,1} \displaystyle \le {{\mathcal {C}}}\, \varDelta x_{n,1}v^{\alpha ,\beta }(x_{n,2}), \end{aligned}$$

(44)

where $\varDelta x_{n,i}=x_{n,i+1}-x_{n,i}$, $i=1,\ldots ,n-1$ and ${{\mathcal {C}}}\ne {{\mathcal {C}}}(n)$.

Proof

We recall that the nodes of the quadrature rule (41) are $x_{n,1}=0$ and $x_{n,2},\ldots ,x_{n,n}$ the zeros of the Jacobi polynomial

$$\begin{aligned} p_{n-1}^{\alpha ,\beta +1}(x)=\gamma _{n-1}^{\alpha ,\beta +1}x^{n-1}+\mathrm {lower \, degree \, terms}, \quad \gamma _{n-1}^{\alpha ,\beta +1}>0, \end{aligned}$$

orthonormal with respect to the weight $v^{\alpha ,\beta +1}(x)=(1-x)^{\alpha }x^{\beta +1}$ on the interval [0, 1]. Denoting by $l_{n,i}(x)$, $i=1,\ldots ,n$, the fundamental Lagrange polynomials based on the system of knots $\{x_{n,1},\ldots ,x_{n,n} \}$, for the coefficients of the quadrature formula (41) we can write

$$\begin{aligned} \lambda _{n,i}=\int _0^1 l_{n,i}(x)v^{\alpha ,\beta }(x)dx, \qquad i=1,\ldots ,n. \end{aligned}$$

Taking into account that

$$\begin{aligned} l_{n,i}(x)=\left\{ \begin{array}{ll}\displaystyle \frac{p_{n-1}^{\alpha ,\beta +1}(x)}{p_{n-1}^{\alpha ,\beta +1}(x_{n,1})}, &{} \quad i=1 \\ \displaystyle \frac{xp_{n-1}^{\alpha ,\beta +1}(x)}{x_{n,i}(x-x_{n,i})(p_{n-1}^{\alpha ,\beta +1})'(x_{n,i})}, &{} \quad i=2,\ldots ,n, \end{array} \right. \end{aligned}$$

we have

$$\begin{aligned} \lambda _{n,1}=\int _0^1 \frac{p_{n-1}^{\alpha ,\beta +1}(x)}{p_{n-1}^{\alpha ,\beta +1}(x_{n,1})}v^{\alpha ,\beta }(x) dx = \int _0^1 \left[ \frac{p_{n-1}^{\alpha ,\beta +1}(x)}{p_{n-1}^{\alpha ,\beta +1}(x_{n,1})}\right] ^2v^{\alpha ,\beta }(x) dx \end{aligned}$$

(45)

and

$$\begin{aligned} \lambda _{n,i}=\frac{1}{x_{n,i}}\int _0^1 \frac{p_{n-1}^{\alpha ,\beta +1}(x)}{(x-x_{n,i})(p_{n-1}^{\alpha ,\beta +1})'(x_{n,i})}v^{\alpha ,\beta +1}(x)dx, \qquad i=2,\ldots ,n. \end{aligned}$$

Then, for $i=2,\ldots ,n-1$, one has that (see [16])

$$\begin{aligned} \lambda _{n,i} \sim \frac{1}{x_{n,i}}\frac{\sqrt{1-x^2}}{n} v^{\alpha ,\beta +1}(x), \qquad x_{n,i} \le x \le x_{n,i+1} \end{aligned}$$

from which, since

$$\begin{aligned} x_{n,i} \sim x \sim x_{n,i+1}, \quad \mathrm {and} \quad 1+x_{n,i} \sim 1 + x \sim 1 + x_{n,i+1}, \qquad x_{n,i} \le x \le x_{n,i+1} \end{aligned}$$

(46)

and

$$\begin{aligned} \varDelta x_{n,i}=x_{n,i+1}-x_{n,i} \sim \frac{\sqrt{1-x^2}}{n}, \qquad x_{n,i} \le x \le x_{n,i+1} \end{aligned}$$

(47)

(see, for instance, [12]), we have

$$\begin{aligned} \lambda _{n,i} \sim \left\{ \begin{array}{ll} \displaystyle \frac{1}{x_{n,i}}\frac{\sqrt{1-x_{n,i}^2}}{n} v^{\alpha ,\beta +1}(x_{n,i}) \sim \varDelta x_{n,i} v^{\alpha ,\beta }(x_{n,i}) &{} \quad i=2,\ldots ,n-1 \\ \displaystyle \frac{1}{x_{n,i}}\frac{\sqrt{1-x_{n,i-1}^2}}{n} v^{\alpha ,\beta +1}(x_{n,i})\sim \varDelta x_{n,i-1}v^{\alpha ,\beta }(x_{n,i}) &{} \quad i=n.\end{array} \right. \end{aligned}$$

It remains to prove (44). To this end, starting from (45), we rewrite the coefficient $\lambda _{n,1}$ as

$$\begin{aligned} \lambda _{n,1}=\left[ \frac{\left( p_{n-1}^{\alpha ,\beta +1}\right) '(x_{n,2})}{p_{n-1}^{\alpha ,\beta +1}(x_{n,1})}\right] ^2 \int _0^1 \frac{\left[ p_{n-1}^{\alpha ,\beta +1}(x)\right] ^2}{\left[ (x-x_{n,2}) \left( p_{n-1}^{\alpha ,\beta +1}\right) '(x_{n,2})\right] ^2}\frac{(x-x_{n,2})^2}{x}v^{\alpha ,\beta +1}(x)dx. \end{aligned}$$

(48)

In what follows we will denote by $x_{n-1,i}^{\alpha ,\beta +1}$ and $\lambda _{n-1,i}^{\alpha ,\beta +1}$, $i=1,\ldots ,n-1$, the nodes and coefficients of the $(n-1)$–point Gaussian quadrature formula on [0, 1] w.r.t. the weight $v^{\alpha ,\beta +1}(x)$. According to this notation, it is $x_{n,2}=x_{n-1,1}^{\alpha ,\beta +1}$.

From (48), being $\frac{(x-x_{n,2})^2}{x} \le {{\mathcal {C}}}$ (also in virtue of (46)), we can deduce that (see, for instance, [17, p. 170])

$$\begin{aligned} \lambda _{n,1} &\le {{\mathcal {C}}}\;\left[ \frac{\left( p_{n-1}^{\alpha ,\beta +1}\right) '(x_{n-1,1}^{\alpha ,\beta +1})}{p_{n-1}^{\alpha ,\beta +1}(0)}\right] ^2 \lambda _{n-1,1}^{\alpha ,\beta +1}\\ &=\, \frac{{{\mathcal {C}}}}{\left[ p_{n-1}^{\alpha ,\beta +1}(0)\right] ^2}\left( \frac{\gamma _{n-1}^{\alpha ,\beta +1}}{\gamma _{n-2}^{\alpha ,\beta +1}}\right) ^2 \frac{1}{\lambda _{n-1,1}^{\alpha ,\beta +1}\left[ p_{n-2}^{\alpha ,\beta +1}(x_{n-1,1}^{\alpha ,\beta +1}) \right] ^2}. \end{aligned}$$

Now, since (see [19, (12.7.2), p. 309], [17, Theorem 9.33 p. 171], [18, (14) and (18), p. 673-674], [12, (4.2.30), p. 255])

$$\begin{aligned} \frac{\gamma _{n-1}^{\alpha ,\beta +1}}{\gamma _{n-2}^{\alpha ,\beta +1}} \sim 1, \quad \left| p_{n-1}^{\alpha ,\beta +1}(0)\right| \sim n^{\beta +\frac{3}{2}}, \quad \lambda _{n-1,1}^{\alpha ,\beta +1} \sim \frac{1}{n^{2\beta +4}}, \quad \left| p_{n-2}^{\alpha ,\beta +1}(x_{n-1,1}^{\alpha ,\beta +1})\right| \sim n^{\beta +\frac{3}{2}} \end{aligned}$$

we get

$$\begin{aligned} \lambda _{n,1} \le {{\mathcal {C}}}\frac{1}{n^{2\beta +2}}. \end{aligned}$$

(49)

On the other hand, it can be easily seen that

$$\begin{aligned} \varDelta x_{n,1}v^{\alpha ,\beta }(x_{n,2}) \sim \frac{1}{n^{2\beta +2}}, \end{aligned}$$

(50)

hence, combining (49) with (50) we get (44) and the proof is complete. $\square$

Theorem 9

Let$F \in W_r^1(v^{\alpha ,\beta })$, $r\ge 1$. Then

$$\begin{aligned} |e_n(F)| \le \frac{{{\mathcal {C}}}}{n^r}E_{2n-2-r}(F^{(r)})_{\varphi ^r v^{\alpha ,\beta },1} \end{aligned}$$

(51)

where ${{\mathcal {C}}}\ne {{\mathcal {C}}}(n,F)$.

Proof

We first prove (51) when $r=1$. To this aim, we start showing the following inequality

$$\begin{aligned} \sum _{i=1}^n\lambda _{n,i}|F(x_{n,i})| \le {{\mathcal {C}}}\Vert Fv^{\alpha ,\beta }\Vert _1+\frac{{{\mathcal {C}}}}{n}\int _0^1|F'(x)|\varphi (x)v^{\alpha ,\beta }(x)dx. \end{aligned}$$

(52)

In virtue of Lemma 3 we can write

$$\begin{aligned} \sum _{i=1}^n\lambda _{n,i}|F(x_{n,i})| &\le {} {{\mathcal {C}}}\left[ \varDelta x_{n,1}v^{\alpha ,\beta }(x_{n,2})|F(x_{n,1})|+\sum _{i=2}^{n-1}\varDelta x_{n,i}v^{\alpha ,\beta }(x_{n,i})|F(x_{n,i})| \right. \\&+\, \left. \varDelta x_{n,n-1} \, v^{\alpha ,\beta }(x_{n,n})|F(x_{n,n})|\right] \end{aligned}$$

from which, using the inequality

$$\begin{aligned} \left. \begin{array}{l} (b-a)|F(a)|\\ (b-a)|F(b)|\end{array}\right\} \le \int _a^b |F(x)|dx+(b-a)\int _a^b |F'(x)|dx, \end{aligned}$$

we get

$$\begin{aligned} \sum _{i=1}^n\lambda _{n,i}|F(x_{n,i})| &\le {{\mathcal {C}}} \left[ v^{\alpha ,\beta }(x_{n,2})\int _{x_{n,1}}^{x_{n,2}}|F(x)|dx+v^{\alpha ,\beta }(x_{n,2})\varDelta x_{n,1} \int _{x_{n,1}}^{x_{n,2}}|F'(x)|dx\right. \\&+ \left. \sum _{i=2}^{n-1}\left( v^{\alpha ,\beta }(x_{n,i})\int _{x_{n,i}}^{x_{n,i+1}}|F(x)|dx+v^{\alpha ,\beta }(x_{n,i})\varDelta x_{n,i} \int _{x_{n,i}}^{x_{n,i+1}}|F'(x)|dx \right) \right. \\&+ \left. v^{\alpha ,\beta }(x_{n,n})\int _{x_{n,n-1}}^{x_{n,n}}|F(x)|dx+v^{\alpha ,\beta }(x_{n,n})\varDelta x_{n,n-1} \int _{x_{n,n-1}}^{x_{n,n}}|F'(x)|dx\right] . \end{aligned}$$

Now, taking into account (46) and (47), we obtain

$$\begin{aligned} \sum _{i=1}^n\lambda _{n,i}|F(x_{n,i})| &\le {{\mathcal {C}}}\left[ \int _{x_{n,1}}^{x_{n,n}}|F(x)|v^{\alpha ,\beta }(x)dx + \frac{1}{n}\int _{x_{n,1}}^{x_{n,n}}|F'(x)|\varphi (x)v^{\alpha ,\beta }(x)dx\right] \\&\le {{\mathcal {C}}}\left[ \int _{0}^{1}|F(x)|v^{\alpha ,\beta }(x)dx+ \frac{1}{n}\int _{0}^{1}|F'(x)|\varphi (x)v^{\alpha ,\beta }(x)dx\right] \end{aligned}$$

i.e. (52). From (52), being the algebraic degree of the exactness of the formula (41) equal to $2n-2$, for each polynomial $P \in \mathbb {P}_{2n-2}$ we can write

$$\begin{aligned} |e_n(F)| &= \left| \int _0^1[F(x)-P(x)]v^{\alpha ,\beta }(x)dx+\sum _{i=1}^n\lambda _{n,i}[F(x_{n,i})-P(x_{n,i})]\right| \\ &\le \Vert v^{\alpha ,\beta }(F-P)\Vert _1+\sum _{i=1}^n\lambda _{n,i}|F(x_{n,i})-P(x_{n,i})| \\ & \le {{\mathcal {C}}}\Vert v^{\alpha ,\beta }(F-P)\Vert _1+ \frac{{{\mathcal {C}}}}{n}\Vert v^{\alpha ,\beta }(F-P)'\varphi \Vert _1. \end{aligned}$$

Then, since (see, for instance, [12, 14])

$$\begin{aligned} \Vert v^{\alpha ,\beta }(F-P)'\varphi \Vert _1 \le {{\mathcal {C}}}(2n-1) \Vert v^{\alpha ,\beta }(F-P)\Vert _1 + {{\mathcal {C}}}_1 E_{2n-3}(F')_{\varphi v^{\alpha ,\beta },1}, \end{aligned}$$

we have

$$\begin{aligned} |e_n(F)| \le {{\mathcal {C}}}\Vert v^{\alpha ,\beta }(F-P)\Vert _1+ \frac{{{\mathcal {C}}}_1}{n}E_{2n-3}(F')_{\varphi v^{\alpha ,\beta },1}. \end{aligned}$$

Now, taking the infimum over $P \in \mathbb {P}_{2n-2}$ and using the Favard inequality (43),

$$\begin{aligned} |e_n(F)| &\le {{\mathcal {C}}}E_{2n-2}(F)_{v^{\alpha ,\beta },1}+\frac{{{\mathcal {C}}}_1}{n}E_{2n-3}(F')_{\varphi v^{\alpha ,\beta },1} \\&\le \frac{{{\mathcal {C}}}}{n} E_{2n-3}(F')_{\varphi v^{\alpha ,\beta },1}. \end{aligned}$$

Iterating the Favarde inequality, we get the estimate (51). $\square$