An extended Hamiltonian QR algorithm

Abstract

An extended QR algorithm specifically tailored for Hamiltonian matrices is presented. The algorithm generalizes the customary Hamiltonian QR algorithm with additional freedom in choosing between various possible extended Hamiltonian Hessenberg forms. We introduced in Ferranti et al. (Calcolo, 2015. doi:10.1007/s10092-016-0192-1) an algorithm to transform certain Hamiltonian matrices to such forms. Whereas the convergence of the classical QR algorithm is related to classical Krylov subspaces, convergence in the extended case links to extended Krylov subspaces, resulting in a greater flexibility, and possible enhanced convergence behavior. Details on the implementation, covering the bidirectional chasing and the bulge exchange based on rotations are presented. The numerical experiments reveal that the convergence depends on the selected extended forms and illustrate the validity of the approach.

1 Introduction

A Hamiltonian matrix $\widehat{H}\in \mathbb {C}^{2n\times 2n}$ is a $2\times 2$ block matrix defined as follows

$$\begin{aligned} \widehat{H} = \begin{bmatrix} \widehat{A}&\quad \widehat{G} \\ \widehat{F}&\quad -\widehat{A}^{H} \end{bmatrix}, \end{aligned}$$

(1.1)

with $\widehat{A},\widehat{F},\widehat{G}\in \mathbb {C}^{n\times n}$, and $\widehat{F}=\widehat{F}^{H}$, $\widehat{G}=\widehat{G}^{H}.$ Hamiltonian matrices are related to the numerical solution of algebraic Riccati equations [8] and can be used in several applications, e.g., in control theory [22, 26].

The Hamiltonian structure has its impact on the spectrum, which is symmetric with respect to the imaginary axis. Classical dense eigenvalue solvers simply ignore this structure, but algorithms designed specifically for Hamiltonian matrices exploit this structure to gain in accuracy and speed [5, 12]. E.g., the Hamiltonian QR algorithm exploits this structure; unfortunately, designing such an algorithm is far from being trivial and so far, only the $\hbox {rank }\widehat{F}=1$ case has been satisfactorily solved [12]. Another fruitful approach is based on forming a URV factorization of $\widehat{H}$ [7, 14, 27, 37].

We will focus on QR type algorithms. The QR algorithm has two main steps: there is a preprocessing step, in which the matrix is transformed to an upper Hessenberg matrix by unitary similarity transformations; and there is the actual processing step, in which the eigenvalues of the latter matrix are retrieved by an iterative process, the QR iteration, preserving the Hessenberg form.

It has been shown recently by Vandebril and Watkins [30, 31] that it is possible to design an effective QR algorithm, based on a condensed form different from the Hessenberg one, e.g., for Hessenberg-like, or CMV matrices. These new QR algorithms are called extended QR algorithms and they work on all matrices admitting a QR factorization whose unitary factor Q can be written as a product of $n-1$ Givens rotations. A more detailed introduction to extended QR algorithms is given in Sect. 1.4.

The QR algorithm [17, 18, 39] computes the spectrum of a Hamiltonian matrix $\widehat{H}$ in a backward stable manner. This means that the computed eigenvalues will be the exact eigenvalues of a nearby (not necessarily Hamiltonian) matrix $\widetilde{H}$, but the symmetry with respect to the imaginary axis may be lost. Byers’s Hamiltonian QR algorithm [12] is a structured variant of the QR algorithm preserving the Hamiltonian structure at each step of the algorithm and thus the symmetry of the spectrum. This results in a structured backward stable algorithm [29]: the computed eigenvalues will be the exact eigenvalues of a nearby Hamiltonian matrix. The benefits of an algorithm preserving the Hamiltonian structure and the effect on the condition numbers of eigenvalues and invariant spaces are discussed in [5, Sect. 3.2]. Moreover, the Hamiltonian QR algorithm roughly halves the required storage and the number of required floating point operations [12].

Our contribution is a generalization of the Hamiltonian QR algorithm to an extended Hamiltonian QR algorithm for Hamiltonian matrices having $\hbox {rank }\widehat{F}=1$. The first step of the algorithm: the reduction to a suitable condensed form, the extended Hamiltonian Hessenberg form, has been described in [15, 16]. The second step, that is the QR iteration preserving the condensed form, is described in this paper.

The paper is organized as follows. In the remainder of this section we will briefly review the (K)-Hamiltonian structure, unitary core transformations, and the extended QR algorithm. In Sect. 2 we will present the extended (K)-Hamiltonian QR iteration, followed by a section on implementation details. In Sect. 3 we present numerical experiments to investigate the accuracy and effect of the various extended forms on the convergence speed. The paper concludes with Sect. 4.

In the rest of the paper we denote the identity matrix of size n by $I_{n}$ and the flip matrix of size n by

We will write I and $\Phi$, when the size is clear from the context, and we will denote by $e_{j}$ the j-th column of the identity matrix. We recall that a matrix is said to be per-Hermitian if $\Phi A$ is Hermitian [11].

The matrix $M^{H}$ is the Hermitian conjugate of M, while with $M(i:j,k:\ell )$, with $i<j$ and $k<\ell$, we address the submatrix with row indices $\{i,i+1,\cdots , j\}$ and column indices $\{k,k+1,\cdots ,\ell \}$ following Matlab notation.

1.1 K-Hamiltonian structure

To ease the description of the algorithm we will use K-Hamiltonian matrices, instead of Hamiltonian ones. A matrix $H\in \mathbb {C}^{2n\times 2n}$ is said to be K-Hamiltonian if $\widehat{H}=KHK$ is a Hamiltonian matrix, with

$$\begin{aligned} K =\begin{bmatrix} I_{n}&\quad 0\\0&\quad \Phi _{n} \end{bmatrix}. \end{aligned}$$

(1.2)

The K-Hamiltonian structure is a permutation of the Hamiltonian structure, which allows us to simplify the algorithm and link it back in an easy manner to the classical QR and extended QR algorithms [31, 38]. The definition of K-Hamiltonian matrices leads to the following proposition.

Proposition 1.1

Let $H\in \mathbb {C}^{2n\times 2n}$ be a K-Hamiltonian matrix. Then H admits the following block structure

$$\begin{aligned} H =\begin{bmatrix} A&G \\ F&-\Phi A^{H}\Phi \end{bmatrix}, \end{aligned}$$

with $G\Phi$ and $\Phi F$ Hermitian and $A,F,G\in \mathbb {C}^{n\times n}$.

Proof

From the definition we have that $\widehat{H} = KHK$ is a Hamiltonian matrix, and thus

$$\begin{aligned} \widehat{H} = KHK = \begin{bmatrix} I&\quad 0\\0&\quad \Phi \end{bmatrix}\begin{bmatrix} A&\quad G \\ F&\quad -\Phi A^{H}\Phi \end{bmatrix}\begin{bmatrix} I&\quad 0\\ 0&\quad \Phi \end{bmatrix} = \begin{bmatrix} A&\quad G\Phi \\ \Phi F&\quad -A^{H} \end{bmatrix}. \end{aligned}$$

It follows that F and G are per-Hermitian, i.e., $G\Phi =(G\Phi )^{H}= \Phi G^{H}$. $\square$

A K-Hamiltonian matrix H with A of upper Hessenberg form and $F = \alpha e_{1}e_{n}^{T}$ is named a K-Hamiltonian upper Hessenberg matrix, which pictorially looks like

A practical advantage of the K-Hamiltonian structure, over the Hamiltonian one, is that every K-Hamiltonian upper Hessenberg matrix is also of upper Hessenberg form.

Following the definition of the K-Hamiltonian matrix above, we call the matrix $S\in \mathbb {C}^{2n\times 2n}$ K-symplectic if KSK is symplectic, where $\widehat{S}\in \mathbb {C}^{2n\times 2n}$ is symplectic if $\widehat{S}^{H} \left[ {\begin{matrix}0&II&0\end{matrix}}\right] \widehat{S} = \left[ {\begin{matrix}0&II&0\end{matrix}}\right]$. K-symplectic matrices are useful in the design of structure preserving algorithms as we see in the next results.

Lemma 1.2

(see [28]) Let $H,S\in \mathbb {C}^{2n\times 2n}$ be a K-Hamiltonian and a K-symplectic matrix respectively, then $SHS^{-1}$ is K-Hamiltonian.

Every K-Hamiltonian matrix with $\hbox {rank } F=1$ can be transformed into a K-Hamiltonian upper Hessenberg matrix by unitary K-symplectic similarity transformations [1]. We can give a simple characterization of unitary K-symplectic matrices which will be useful in the following.

Theorem 1.3

A unitary matrix $S\in \mathbb {C}^{2n\times 2n}$ is K-symplectic if and only if it can be written as

$$\begin{aligned} S=\begin{bmatrix} U_{1}&U_{2}\Phi \\ -\Phi U_{2}&\Phi U_{1}\Phi \end{bmatrix} \end{aligned}$$

for matrices $U_{1},U_{2}\in \mathbb {C}^{n\times n}$. In particular, if S has a block diagonal structure

$$\begin{aligned} S=\begin{bmatrix} I_{n-1}\\&Q\\&I_{n-1} \end{bmatrix}, \end{aligned}$$

with $Q\in \mathbb {C}^{2\times 2}$, then

$$\begin{aligned} Q=e^{i\psi }\begin{bmatrix} \cos \theta&-\sin \theta \\ \sin \theta&\cos \theta \end{bmatrix}, \end{aligned}$$

for some $\psi ,\theta \in [0,2\pi )$.

Proof

It is well-known that a unitary symplectic matrix T has the form for $U_{1},U_{2}\in \mathbb {C}^{n\times n}$; see, for instance, [8, Thm. 1.16]. Observing that KSK is unitary and symplectic we get the result. $\square$

As a consequence of Theorem 1.3, real rotations involving rows n and $n+1$ are K-symplectic. A special case of K-symplectic matrices are block diagonal K-symplectic matrices, which have the form

$$\begin{aligned} S=\begin{bmatrix} S_{11}&0\\0&S_{22} \end{bmatrix},\quad \text{ with } \quad S_{22}^{H}=\Phi S_{11}^{-1}\Phi . \end{aligned}$$

If, additionally, S is unitary, then $S_{22}=\Phi S_{11}\Phi$ and both, $S_{11}$ and $S_{22}$, are unitary.

1.2 Unitary core transformation

In this section and in the following we define unitary core transformations and their K-symplectic generalizations. Then, we will briefly review the most important operations with these transformations.

We call any matrix $Q_i\in \mathbb {C}^{n\times n}$, for $i\in \{1,\ldots ,n-1\}$, coinciding with the identity matrix except for the $2\times 2$ submatrix $Q_i(i:i+1,i:i+1)$ a core transformation. The index i describes the position of the active part $Q_i(i:i+1,i:i+1)$. A unitary core transformation is said to be nontrivial if it is not diagonal.

A special subset of unitary core transformations are the rotations acting on two consecutive coordinates, with active part $\left[ {\begin{matrix} c&{} -\overline{ s}\\ {s} &{} \overline{c}\end{matrix}}\right]$, where $\left|c\right|^{2}+\left|s\right|^{2}=1$. We will use frequently to depict a core transformation, where the tiny arrows pinpoint the position of the active part, as illustrated in the next example. In the remainder of the text we assume all core transformations to be rotations.

Example 1.4

The QR decomposition of an upper Hessenberg matrix $A\in \mathbb {C}^{n\times n}$ can be written as

$$\begin{aligned} A = QR = Q_{1}Q_{2}\cdots Q_{n-1} R, \end{aligned}$$

where the matrices $Q_{i}$ are rotations. Pictorially, by using the bracket notation, the QR decomposition is depicted as ($n=9$)

The unitary factor Q of the QR factorization of an Hessenberg matrix, as shown in Example 1.4, can be written as a product of rotations, each of which acts on two consecutive rows. The order in which rotations appear is $(1,\ldots ,n-1)$.

Definition 1.5

An extended Hessenberg matrix is a matrix that admits a QR where the unitary factor Q can be factored into $n-1$ core transformations $Q=Q_{\sigma (1)}\cdots Q_{\sigma (n-1)}$ for a specific permutation $\sigma$.

If all the matrices $Q_1,\ldots ,Q_{n-1}$ are nontrivial, then the extended Hessenberg matrix is said to be irreducible. The permutation associated with an extended Hessenberg matrix is not always unique as $Q_iQ_j=Q_jQ_i$ as soon as $|i-j|>1$, for instance, observe that $Q_1Q_3Q_2=Q_3Q_1Q_2$. In order to get uniqueness results, the mutual position of the rotations in the Q factor of an extended Hessenberg matrix is described by a pattern, given by a position vector $p\in \{\ell ,r\}^{n-2}$ defined as follows:

$$\begin{aligned} p_{i}= {\left\{ \begin{array}{ll} \ell , &{} \text {if } Q_{i} \text { is on the left of } Q_{i+1}, \\ r, &{} \text {if } Q_{i} \text { is on the right of } Q_{i+1}. \end{array}\right. } \end{aligned}$$

The pattern associated with the Q factor of an irreducible extended Hessenberg matrix is uniquely defined [15, Cor. 4]; in case of an irreducible matrix the eigenvalue problem splits into smaller subproblems. So, without loss of generality, we can assume irreducibility before running QR steps.

Two factorizations in rotations share the same pattern if they can be ordered so that the graphical representation by brackets exhibits the same pattern. Note that this definition does not imply equality of the rotations but only their position in the factorization of Q.

The rotations in the QR factorization of an upper Hessenberg matrix are ordered according to $p=(\ell ,\cdots ,\ell )$. An inverse Hessenberg matrix corresponds to $p=(r,\cdots ,r)$, the position vector of a unitary CMV matrix¹ equals $p=(\ell , r, \ell , r , \cdots )$. The following pictorial representations show these matrices and an arbitrary unstructured position vector.

As rotations acting on disjoint rows commute, there is no ambiguity in putting rotations on top or below each other as in the CMV or arbitrary case presented above.

As proved in [30], extended Hessenberg matrices can be used as a condensed form for a QR type algorithm: the so-called extended QR algorithm, requiring also $\mathcal {O}(n^{2})$ storage and $\mathcal {O}(n^{3})$ flops [30]. The name extended refers to the convergence behavior of the extended QR algorithm which is governed by extended Krylov subspaces [23, 31].

1.3 Unitary K-symplectic core transformations

K-symplectic matrices preserve the K-Hamiltonian structure; as we focus on QR type algorithms we need unitary K-symplectic matrices. We consider K-symplectic core transformations of two types: $Q^{S}_{i}=Q_{i}Q_{2n-i}$ for $i<n$, with active parts fulfilling $Q_{i}(i:i+1,i:i+1)=\Phi Q_{2n-i}(2n-i:2n-i+1,2n-i:2n-i+1)\Phi$; and $Q^S_{n}=Q_{n}$, where the active part $Q_{n}(n:n+1,n:n+1)=e^{i\psi }\left[ {\begin{matrix}c &{} -s\\ s &{} c\end{matrix}}\right]$, with $\psi ,c,s\in \mathbb {R}$. In particular $Q_{n}(n:n+1,n:n+1)$ could be a real rotation.

Since K-symplectic rotations have a simple structure we have decided to restrict the rest of the paper to rotations only. In order to design the extended QR algorithm, we need some ways to manipulate rotations: we use the fusion (to fuse), the turnover (to turn over), and the transfer through an upper triangular (to transfer through) operations.

The product of two rotations acting on the same rows of a matrix is a new rotation, This operation is called fusion and is depicted as . As a result, also the product of two (K-)symplectic rotations acting on the same rows is a (K-)symplectic rotation and a fusion can be applied.

If $U_{k+1}$ and $W_{k+1}$ are two rotations acting on rows $k+1$ and $k+2$ of a matrix, and $V_{k}$ is a rotation acting on rows k and $k+1$, then three rotations $\widetilde{U}_{k},\widetilde{V}_{k+1}$, and $\widetilde{W}_{k}$ exist, such that $\widetilde{U}_{k}$ and $\widetilde{W}_{k}$ act on rows k and $k+1$, $\widetilde{V}_{k+1}$ acts on rows $k+1$ and $k+2$, and $U_{k+1}V_{k}W_{k+1}=\widetilde{U}_{k}\widetilde{V}_{k+1}\widetilde{W}_{k}$. The result is graphically depicted as

We call this operation a turnover. Indeed, switching from the one factorization to the other we turn over the shape of the rotations. Again, we can generalize this to (K-)symplectic rotations with $i\ne n$, where two turnovers, one in the lower and one in the upper half are executed simultaneously.

If we apply a rotation from the left to a nonsingular upper triangular matrix, then an unwanted non-zero entry in the lower triangular part is created. This non-zero entry can be removed by pulling out a rotation from the right. Graphically this process can be depicted as

where the second and third row and column are altered in the process. This operation will be used in both directions; from left to right and from right to left and is the transfer through an upper triangular operation. This operation extends naturally to (K-)symplectic rotations.

1.4 Extended QR algorithms

In this subsection the extended QR algorithm is presented (for more info see [30, 31]). For simplicity we restrict ourselves to explain the complex single shift case.

1.4.1 Chasing misfits instead of bulges

The extended QR algorithm uses, as a condensed form, extended Hessenberg matrices, written as a product of rotations and an upper triangular matrix as described in Sect. 1.2.

Before describing the general case, we consider the case in which the condensed matrix is of Hessenberg form. In this case, one step of the extended QR algorithm is identical to one step of the customary QR algorithm. However, in the latter case we operate on the Hessenberg matrix, whereas in the first case on its QR factorization. Operating on the Hessenberg matrix leads to the usual “chase the bulge” procedure, acting on the factored form is a “chase the misfit” procedure. In the upcoming figures, the bulge chase is depicted on the right, the misfit-chasing is shown on the left.

The iteration starts by picking a shift $\mu$ (typically an eigenvalue of the trailing $2\times 2$ submatrix [40]), and by computing a rotation $B_{1}$ that fulfills

$$\begin{aligned} B_{1}^{H}\left( Q_{1} \begin{bmatrix} r_{11} \\ 0\\ \vdots \\ 0 \end{bmatrix} - \begin{bmatrix} \mu \\ 0\\ \vdots \\ 0 \end{bmatrix}\right) = B_{1}^{H} \begin{bmatrix} a_{11} - \mu \\ a_{21}\\ 0\\ \vdots \\ 0 \end{bmatrix} = \begin{bmatrix} \times \\ 0\\ 0 \\ \vdots \\ 0 \end{bmatrix}. \end{aligned}$$

Next, the similarity transformation $B_{1}^{H}QRB_{1}=B_{1}^{H}AB_{1}$ is executed. Pictorially, for $n=4$ we have

In the classical Hessenberg case the matrix multiplication is performed explicitly and a bulge, shown in the right-hand side of (1.3) is created. On the left-hand side, we retain a factored form. The rotation $B_{1}^{H}$ is therefore fused with $Q_{1}$, and we transfer the rotation $B_{1}$ on the right through the upper triangular matrix. We notice a remaining redundant rotation, that is the misfit, and it will be chased off the matrix.

Pictorially, we end up with

(1.3)

Next we will try to chase the bulge on the right-hand side and the misfit on the left-hand side. To do so, we first perform a turnover on the left and on the right we annihilate the bulge by pulling out a rotation.

The leftmost rotations on both sides are essentially identical and can be brought simultaneously to the other side by a single similarity transformation. New rotations emerge on the right of both matrices. Next, we transfer the rotation through the upper triangular matrix (left-hand side) or apply it to the upper Hessenberg matrix (right-hand side). Pictorially, we have

Clearly the bulge and the misfit have moved down. We continue now this procedure until the bulge and misfit slide off the bottom of the matrix.

An identical procedure as before, a turnover on the left and pulling out a rotation on the right, leads to

A last chase, a similarity transformation, a transfer through upper triangular, and a fusion, restore the upper Hessenberg form on the left. Also on the right after the similarity and multiplying out the factors we get a new Hessenberg matrix. This completes one step of the (extended) QR algorithm with implicit shift.

Overall, every step of the QR-like algorithm proceeds as follows: create a perturbation (bulge or misfit), chase the perturbation to the bottom of the matrix, and finally push it off the matrix. Iterating this process will make the matrix closer and closer to a reducible form allowing to subdivide (deflate) the problem in smaller subproblems. Deflations are signaled by tiny subdiagonal elements in the Hessenberg case and rotations close to the identity in the factored form. From now on we focus only on the factored form.

1.4.2 Extended QR iteration

The extended QR algorithm works essentially in the same way as the misfit chasing presented in Sect. 1.4.1 but with an arbitrary extended Hessenberg matrix as condensed form. We execute an initial similarity transformation creating an auxiliary rotation called the misfit, we chase the misfit, and finally get rid of it by a fusion. More in detail we get the following.

First we generate the misfit. Compute

$$\begin{aligned} x&=(A-\mu I)e_{1}= Q_{1} \begin{bmatrix} r_{11} \\ 0 \end{bmatrix} - \begin{bmatrix} \mu \\ 0 \end{bmatrix},&\text {if}\quad p_{1}=\ell , \quad \text {or}\nonumber \\ x&=(I-\mu A^{-1})e_{1} = e_{1} - \mu R^{-1} Q_{1}^{H}e_{1},&\text {if}\quad p_{1}=r. \end{aligned}$$

(1.4)

Notice that in both cases only $Q_{1}$ and few entries of R are required. Once x has been obtained we compute the rotation $B_{1}^{H}$ with $B_{1}^{H}x = \Vert x\Vert e_1.$ After applying the similarity transformation determined by $B_{1}$ and transferred the matrix $B_1$ appearing on the left through the upper triangular matrix, we arrive at the following factorization: $B_1^HQ_{\sigma (1)} \cdots Q_{\sigma (n-1)}\widetilde{B}_1\widetilde{R}$. One between $B_1^H$ and $\widetilde{B}_1$ can be fused and the other one becomes the misfit. More precisely, if $p_1=\ell$, then $B_1^H$ will be fused with $Q_1$ and the misfit will be $\widetilde{B}_1$, while if $p_1=r$, then $Q_1$ will be fused with $\widetilde{B}_1$ and the misfit will be $B_1$.

So far, we have only seen how to chase misfits on descending sequences of rotations (associated with Hessenberg matrices). Suppose for now that we have executed already one chasing step and we have arrived in a situation where the misfit operates on rows two and three and is positioned to the left of the factored matrix. A step of the flow to push the misfit further down is depicted as

where the arrows describe the path the misfit follows.

In the beginning we have the factorization , where is the misfit, $Q_i$ are rotations and R is upper triangular. The matrix acts on rows 2 and 3 and thus commutes with $Q_5$ and $Q_4$ and we can write . The arrow labeled with 1 corresponds to a turnover, where the product is transformed into the product of three new rotations and we get the new factorization ; where we have used the fact that and $Q_1$ commute. The arrow labeled with 2 depicts a transfer through operation on which leads to the new factorization . Finally, the arrow labeled with 3 corresponds to a similarity with , which leads to the new factorization , and the misfit has been shifted down one row.

We know now how to chase rotations in case of a complete descending or a complete ascending sequence. It remains to describe what happens at a bend, i.e., a transition from $\ell$ to r or from r to $\ell$ in the position vector. We will see that in this case the misfit will get stuck and cannot be chased any further to the bottom; on the other hand, however, there is another rotation acting on the same rows which can be chased and therefore will take over the role as misfit.

A bend from descending ($\ell$) to ascending (r) and the associated chasing step can be depicted as

The role of the misfit $B_2$ is overtaken by $Q_{2}$. The arrow labeled with 1 corresponds to a turnover, the one labeled with 2 to a transfer through operation and the one labeled with 4 to a similarity. After these operations we see indeed that the misfit has moved down a row. Moreover, we can also see, when comparing the pattern before and after the chasing step, that the bend has moved up one position; originally it was acting on rows 3 and 4, now on rows 2 and 3.

A bend in the other direction can be done analogously. Pictorially, we get:

Where again we have a turnover (arrow 1), a similarity (arrow 2), followed by a transfer through operation (arrow 3). Also here, clearly the bend has moved up. In fact after all chasing steps the entire pattern will have moved up a row; so the first rotation of the sequence drops off, and at the very end we will have to add a new one as we shall see.

After having completed all chasing steps the misfit has reached the bottom two rows and we have arrived pictorially at:

Now we can make a choice and remove either of the two rotations acting on the last two rows. A similarity, pass through, and fusion are sufficient to remove the left one; a pass through, similarity, and fusion allow us to remove the right one. So we can choose which rotation to retain and which to dispose off. This flexibility, as a result of the upward movement of the pattern, allows us in fact to change the pattern’s tail each QR step. We will see that in the extended Hamiltonian QR algorithm this flexibility is much more limited.

The important difference between the QR algorithm and the extended QR algorithm is the convergence behavior: the classical QR algorithm links to Krylov subspaces [39], the extended QR algorithm links to extended Krylov subspaces [31]. As a result, the convergence speed differs and a cleverly chosen combination of shifts and position vectors can accelerate convergence [30]. We will illustrate this in the numerical experiments.

2 Extended K-Hamiltonian QR iteration

A (K-)Hamiltonian QR algorithm is described in [12]. The main trick is to execute QR steps with shifts $\mu$ simultaneously with RQ steps having shifts $-\overline{\mu }$. Implicitly, this means that one chases a bulge from top to bottom (QR step) and simultaneously a bulge from the bottom to the top (RQ step). In the middle the bulges meet and swap place (bulge exchange) so that they can continue their upward and downward chase. This bidirectional chase has been described for multiple shifts and general matrices in [32, 35]. In our case we will restrict ourselves to the complex single shift case with shifts $\mu$ and $-\overline{\mu }$ and for simplicity we operate on K-Hamiltonian matrices.

In the extended K-Hamiltonian QR algorithm we have to take into account, that in order to preserve the structure, we will only execute unitary K-symplectic transformations and moreover we chase misfits instead of bulges. The algorithm proceeds as follows. First we initialize the procedure by generating two misfits. The chasing is almost identical to the procedure described in Sect. 1.4.2, except that now we chase one misfit down and another one up at the same time, by executing unitary symplectic transformations. The chasing procedure stops as soon as the misfits reach the middle and interfere with each other. To continue, we exchange them and after that we chase them towards the top and bottom of the matrix. This completes one step of the implicit extended K-Hamiltonian QR algorithm.

We point out that the structure of the extended Hessenberg matrices which are moreover K-Hamiltonian allows one to factor them in a symmetric form.²

Definition 2.1

(see [15]) An extended K-Hamiltonian Hessenberg matrix

$$\begin{aligned} H&=\begin{bmatrix} A&G \\ F&-\Phi A^{H}\Phi \end{bmatrix} \end{aligned}$$

can be written as (descending type)

$$\begin{aligned} H&=\begin{bmatrix} Q&0 \\ 0&I \end{bmatrix} \begin{bmatrix} \widetilde{R}&\widetilde{G} \\ \widetilde{F}&-\Phi \widetilde{R}^{H}\Phi \end{bmatrix} \begin{bmatrix} I&0 \\ 0&\Phi Q^{H}\Phi \end{bmatrix}, \end{aligned}$$

(2.1)

with

$$\begin{aligned} \begin{bmatrix} Q&0 \\ 0&I \end{bmatrix}&= Q_{\sigma (1)}Q_{\sigma (2)}\cdots Q_{\sigma (n-1)} \qquad \text {and} \qquad \widetilde{F}=f e_{1}e_{n}^{T}. \end{aligned}$$

An extended K-Hamiltonian Hessenberg matrix is thus completely defined by the sequence $Q_{1},\cdots ,Q_{n-1}$, $\sigma$, f, the upper triangular matrix R, and the upper left triangular part of $\widetilde{G}$, since $\widetilde{G}$ is per-Hermitian.

In Sect. 2.1 we show how to initialize the chasing; Sect. 2.2 describes the chase of the misfits until they meet each other; Sect. 2.3 presents a way to swap the misfits; and finally, in Sect. 2.4 we describe how to continue the chasing until the misfits slide off the matrix.

2.1 Misfit generation

First of all, we have to pick a shift. For the misfit chased from the top to the bottom, the Wilkinson shift is defined by the eigenvalue of the block $H(2n-1:2n,2n-1:2n)$ closest to H(2n : 2n). To retain the K-Hamiltonian structure we have to take $-\overline{\mu }$ as shift for the upward chase.

The rotation $B_1$ to initialize the procedure is the same as the one described in Sect. 1.4.1. The rotation for the upward chase is $\Phi B_1^H \Phi$, which is thus implicitly known. We apply the K-symplectic similarity transformation defined by $B_{1}$ to H, factored as in (2.1), and we get

$$\begin{aligned} \begin{bmatrix} B_{1}^{H}&0\\ 0&\Phi B_{1}^{H}\Phi \end{bmatrix} \begin{bmatrix} Q&0 \\ 0&I \end{bmatrix} \begin{bmatrix} R&G\\ F&-\Phi R^{H}\Phi \end{bmatrix} \begin{bmatrix} I&0 \\ 0&\Phi Q^H \Phi \end{bmatrix} \begin{bmatrix} B_{1}&0 \\ 0&\Phi B_{1}\Phi \end{bmatrix}. \end{aligned}$$

(2.2)

First, we need a fusion to remove already two rotations. Assume here that $p_1=\ell$, thus, we can fuse the top-left $B_1^H$ with $Q_1$, and as a consequence the bottom-right $\Phi B_1 \Phi$ with $\Phi Q_1^H \Phi$. Second, we will pass the top right $B_1$ through R to move it close enough to the sequence of rotations so that the chasing can start; of course a similar action takes place in the lower half where $\Phi B_1^H \Phi$ is passed through $-\Phi R^H\Phi$. We arrive at the following situation

$$\begin{aligned} \begin{bmatrix} \widetilde{Q}&0 \\ 0&I \end{bmatrix} \begin{bmatrix}\widetilde{B}_{1}&0\\ 0&I \end{bmatrix} \begin{bmatrix} \widetilde{R}&\widetilde{G}\\ F&-\Phi \widetilde{R}^{H}\Phi \end{bmatrix} \begin{bmatrix} I&0\\ 0&\Phi \widetilde{B}_{1}\Phi \end{bmatrix} \begin{bmatrix} I&0 \\ 0&\Phi \widetilde{Q}^H \Phi \end{bmatrix} , \end{aligned}$$

(2.3)

with

$$\begin{aligned} \begin{bmatrix} \widetilde{Q}&0 \\ 0&I \end{bmatrix}&= \widetilde{Q}_{\sigma (1)} \cdots Q_{\sigma (n-1)} \end{aligned}$$

(2.4)

$$\begin{aligned} \begin{bmatrix} I&0\\ 0&\Phi \widetilde{Q}^H \Phi \end{bmatrix}&= \Phi Q_{\sigma (n-1)}^{H} \Phi \cdots \Phi \widetilde{Q}_{\sigma (1)}^{H}\Phi . \end{aligned}$$

(2.5)

The matrices with a tilde have been changed during the procedure.

When $p_1=r$, the matrix $B_1^H$ cannot be fused with $Q_1$, but we can fuse $Q_1$ with $\widetilde{B_1}$ (for $n>2$).

2.2 Misfit chasing (before the exchange)

The two misfits that have been generated are chased in opposite directions. The misfit on the top has to be brought to the complete bottom of the matrix; whereas the misfit at the bottom has to move all the way up to the top. Unfortunately, we cannot do this at once as in Sect. 1.4.2. When the two misfits meet each other during their downward and upward move, they block each others way. Therefore we chase the misfit on the left of the upper triangular matrix down until half of the matrix, i.e., until it acts on rows $n-1$ and n. The other misfit is chased upwards until it reaches rows $n+1$ and $n+2$. After that the two misfits interfere with each other and they need to be exchanged. Of course, because of the execution of unitary K-symplectic transformations, preserving the K-Hamiltonian structure, the upward and downward chase are executed simultaneously. In the practical implementation we will operate on R only and update G appropriately.

2.3 Misfit exchange

We have chased the two misfits simultaneously to the middle of the matrix. Since the misfits are blocking each other, further chasing is not possible and, in order to continue the procedure, the misfits must be exchanged.

In [35] Watkins shows that in the implicit QR step, the bulge contains the shift information (as an eigenvalue of a suitable pencil constructed from the bulge) and explains how to exchange two bulges which meet after a chase from opposite directions. The exchange is made preserving the shift information and allowing their further chase until the QR step is concluded.

A similar argument could be used to show that misfits carry the shift information in the implicit step of the extended QR algorithm. Each misfit contains its shift information, that means, the misfit coming from the top should contain $\mu$ and the one coming from the bottom $-\overline{\mu }$. The misfit exchange will swap the shift information contained in the two misfits so that chasing can be continued.

Directly after the chasing and before the misfit exchange we are in the following situation

We remark that this is a generic situation, independent of the value of the last entry of the position vector. Of course this value stipulates that the misfit arrives from the left or from the right to the sequence $Q_{\sigma (1)}\cdots Q_{\sigma (n)}$, but regardless of whether the misfit is positioned left or right, the situation looks like this. Moreover, the bulge exchange does not need to know which one was the misfit.

After a K-symplectic similarity transformation that brings the outermost two rotations to the other side (note that none of the rotations is blocked by other rotations), we end up with

There are only four rotations acting in the bulge exchange, let us therefore focus on the essential block, the $4 \times 4$ one in the middle:

(2.6)

The symmetry imposed by the K-Hamiltonian structure implies that the top-left rotation $C_{n-1}^H$ is related to the bottom-right rotation $\Phi C_{n-1} \Phi$; a similar connection holds for the top-right and bottom-left rotation.

To perform the misfit exchange we form the dense matrix X, so that we are exactly in the same situation as the one arising in the bulge exchange described in [35] and we can apply the argument there.

When the two bulges correspond to one shift each, the shift exchange consists of executing a single unitary K-symplectic similarity transformation acting on rows and columns n and $n+1$, such that we end up with a factorization similar to (2.6) with the important difference that the shift information is exchanged.

Because of its K-Hamiltonian structure $x_{43} = -\overline{x}_{21}$ and $x_{33}=-\overline{x}_{22}$. Note also that the submatrix X(3 : 4, 1 : 2) must be of rank 1. Thus, the K-symplectic unitary transformation acting on rows n and $n+1$, we are looking for, must preserve the rank of that submatrix. We will show that such a similarity transformation is essentially unique, when nontrivial, and thus it performs the misfit exchange.

A K-symplectic similarity transformation operating on the middle rows of X, is a real rotation and hence form

$$\begin{aligned} Y=S_{n}^{H}X S_{n}&= \begin{bmatrix} 1&&\\&c&s&\\&-s&c&\\&&1\\ \end{bmatrix} \begin{bmatrix} x_{11}&x_{12}&x_{13}&x_{14}\\ x_{21}&x_{22}&x_{23}&x_{24}\\ x_{31}&x_{32}&x_{33}&x_{34}\\ x_{41}&x_{42}&x_{43}&x_{44}\\ \end{bmatrix} \begin{bmatrix} 1&&\\&c&-s&\\&s&c&\\&&1\\ \end{bmatrix}\\&= \begin{bmatrix} x_{11}&\quad c x_{12} + s x_{13}&\quad \cdots \\ c x_{21} + s x_{31}&\quad c^{2} x_{22} + cs x_{32} + cs x_{23} + s^{2} x_{33}&\quad \cdots \\ c x_{31} - s x_{21}&\quad c^{2} x_{32}-cs x_{22} +cs x_{33} - s^{2} x_{23}&\quad \cdots \\ x_{41}&\quad c x_{42} + s x_{43}&\quad \cdots \\ \end{bmatrix}, \end{aligned}$$

with $c,s\in \mathbb {R}$. As we desire Y to be of the same form as (2.6), we impose that the submatrix

$$\begin{aligned} \begin{bmatrix} c x_{31} - s x_{21}&\quad c^{2} x_{32}-sc x_{22} +cs x_{33} - s^{2} x_{23} \\ x_{41}&\quad c x_{42} + s x_{43} \\ \end{bmatrix} \end{aligned}$$

(2.7)

has to be of rank 1.

It is easy to show that there are only two possible solutions to this problem, of which one is trivial and hence does not exchange the shift information, while the other one does. We have the trivial solution with $s=0$ and $\left|c\right|=1$, but of course nothing happens and the shifts would not be exchanged. To find the other solution we use the rank 1 structure of (2.7). We have that (2.7) is of rank 1 if and only if

$$\begin{aligned} (c x_{31} - s x_{21})(c x_{42} + s x_{43})&= x_{41}\left( c^{2} x_{32}-sc x_{22} +cs x_{33} - s^{2} x_{23}\right) . \end{aligned}$$

The matrix $\left[ {\begin{matrix} x_{31}&{}x_{32}\\ x_{41}&{}x_{42} \end{matrix}}\right]$ is of rank 1, hence $x_{41}x_{32}=x_{31}x_{42}$. Since $s \ne 0$, the equation above can be rewritten as

$$\begin{aligned} c (- x_{21} x_{42} + x_{31}x_{43} +x_{22}x_{41}-x_{33}x_{41})+ s (- x_{21}x_{43} + x_{23}x_{41}) = 0. \end{aligned}$$

With $x_{43} = -\overline{x}_{21}$, $x_{33}=-\overline{x}_{22}$, and $x_{31}=\overline{x}_{42}$ we obtain

$$\begin{aligned} S_{n} \begin{bmatrix} -x_{41}x_{23} - x_{21}\overline{x}_{21}\\ -x_{21}\overline{x}_{31} - \overline{x}_{21}x_{31} + (x_{22}+\overline{x}_{22})x_{41} \end{bmatrix} = \begin{bmatrix} \times \\ 0 \end{bmatrix}, \end{aligned}$$

(2.8)

which defines $S_{n}$. Since $x_{41},x_{23}\in \mathbb {R}$, the rotation $S_{n}$ is real and thus is a K-symplectic rotation. As the rotation $S_n$ clearly differs from the trivial solution, we know that the shift information must have been exchanged. In the numerical experiments (Sect. 3.2) we will compute the shift information in a bulge and examine how accurately the shift information is exchanged.

To summarize: for the misfit exchange one first has to form X; then one has to compute $S_{n}$ by (2.8) followed by the similarity transformation $M\rightarrow S_{n}^{H}MS_{2}$. Finally, the matrix resulting from the similarity must be factored again like in (2.6) providing the new misfits and updated rotation $Q_{\sigma (n-1)}$.

2.4 Misfit chasing (after the exchange) and final step

The misfit that originally started at the top, carrying the information of the shift $\mu$ is now acting on rows $n+1$ and $n+2$. It is not blocked anymore by the other misfit, and we continue the classical chasing procedure until it reaches the bottom of the matrix and can get fused into the sequence of rotations of the factorization of the K-Hamiltonian Hessenberg matrix. Of course, because of the execution of unitary K-symplectic similarities, the other misfit carrying the information of the shift $-\overline{\mu }$ moves upward until it disappears as well.

There is one more interesting remark related to the final pattern, after the entire chasing, that needs to be made. In the first part of the chasing, before the exchange, we see that the misfit starting at top, has pushed the entire pattern at the upper half up one position. The misfit that started at the bottom pushed the lower half of the pattern down one position. As a consequence the top rotation of the pattern, and the bottom rotation are gone. Continuing the chase after the exchange, the misfit carrying the information of $\mu$ proceeds its way to the bottom and pushes the pattern back up a position. On the other side, the opposite happens, the misfit linked to $-\overline{\mu }$ pushes the pattern back down. Finally at the very end of the chasing step, we have some flexibility in executing the fusion on the left or on the right of the pattern of rotations. As a result we see that the pattern of the rotations in the factorization of the K-Hamiltonian Hessenberg is forced to be identical to the original pattern, except only for the last (and first) rotation, which we could have put either to the left or to the right of the preceding (following) rotations.

2.5 Deflation

An extended K-Hamiltonian Hessenberg matrix is factorized as a product of rotations and a quasi-upper triangular K-Hamiltonian matrix (2.1) where R is upper triangular and $F=fe_{1}e_{n}^{T}$. In extended QR algorithms deflations are signaled by almost diagonal rotations [25]. Additionally, there is the rare but very valuable deflation when $\parallel \!F\!\parallel =\left|f\right|$ becomes small. For this entry, we perform a test of the form $\parallel \!F\!\parallel <\varepsilon (\left|h_{n,n}\right| + \left|h_{n+1,n+1}\right|)$ following [21, Section 1.3.4]. In the K-Hamiltonian we use $\varepsilon (\left|h_{n,n}\right| + \left|h_{n+1,n+1}\right|) = 2 \varepsilon \left|h_{n,n}\right|$ to simplify this criterion to $\parallel \!F\!\parallel <2\varepsilon \left|h_{n,n}\right|$.

When $\left|f\right|$ becomes tiny enough we can split the eigenvalue problem in two parts, since we can decouple the K-Hamiltonian matrix into its upper and lower half. The deflation is valuable since it only remains to compute the eigenvalues of the upper part. We get the eigenvalues of the lower part for free because an eigenvalue $\lambda$ of the top part implies that $-\bar{\lambda }$ is an eigenvalue of the lower part. To compute the eigenvalues of the upper part we do not need to use the K-Hamiltonian QR algorithm anymore, we can just run the extended QR algorithm.

With each regular deflation the matrix splits into three submatrices whose eigenvalues we can compute separately. A deflation in the top part also implies a deflation in the bottom part, hence we have a submatrix before the deflation, a submatrix between the two deflations, and a trailing submatrix following the last deflation. The eigenvalues of the top part can be computed again via the extended QR algorithm. The middle matrix is still of K-Hamiltonian form and we run the K-Hamiltonian QR algorithm. We do not compute the eigenvalues $-\bar{\lambda }$ of the trailing submatrix, as they are for free once the eigenvalues $\lambda$ of the top block are available.

3 Numerical experiments

We have tested our Matlab implementation of the extended Hamiltonian QR algorithm on a compute server with two Intel Xeon E5-2697v3 CPUs running at 2.60 GHz with Matlab version 9.1.0.441655 (R2016b). We tested the accuracy of the bulge exchange in Sect. 3.2; the number of iterations per eigenvalue and the accuracy of the extended QR algorithm in Sect. 3.3; and the performance for different position vectors in Sect. 3.4. We have further tested the code with two examples from the CAREX package [6] in Sect. 3.5. Before discussing the numerical experiments, we will describe some details of the implementation.

3.1 Implementation details

We have implemented the single shift extended Hamiltonian QR algorithm in Matlab. Many subroutines, e.g., fusion and turnover, of the Matlab implementation are based on those of eiscor [2]. Our implementation is available from https://people.cs.kuleuven.be/raf.vandebril/.

We store the factored extended K-Hamiltonian Hessenberg matrix

$$\begin{aligned} H&= \begin{bmatrix} Q&\quad 0 \\ 0&\quad I \end{bmatrix} \begin{bmatrix} R&\quad G \\F&\quad -\Phi R^{H}\Phi \end{bmatrix} \begin{bmatrix} I&\quad 0 \\ 0&\quad \Phi Q^{H}\Phi \end{bmatrix}, \end{aligned}$$

with $Q= Q_{\sigma (1)}Q_{\sigma (2)}\cdots Q_{\sigma (n-1)}$, and $\sigma$ according to the position vector p. We keep only $f_{1n},G,R,p$, and the rotations in Q. For R and G we store the full square matrix. The storage could be optimized for G and R by exploiting the per-Hermitian and the upper triangular structure, respectively.

For the implementation we use rotations $\left[ {\begin{matrix} c &{} -s\\ s &{} \overline{c} \end{matrix}}\right]$ with real sine, $s\in \mathbb {R}$, and $\left|c\right|^{2}+s^{2}=1$, thus, for each rotation we store only three real values. Furthermore, rotations with real sines are advantageous, since a turnover of three rotations with real sines results again in three rotations with real sines. The result of a fusion of two rotations with real sines, however, is a rotation with a possible complex sine. By multiplying the rotation by a diagonal matrix the rotation can be transformed back into a rotation with real sine. The diagonal matrix can be passed through other rotations and merged into the upper triangular matrix R.

Additionally, one may choose to do two preparation steps. Eigenvalues should be deflated if the structure allows it, so that the resulting extended K-Hamiltonian Hessenberg matrix is irreducible. Further, the accuracy of the computations typically benefits from balancing the matrix (see also [36]). These steps have been investigated in [3] for dense matrices and in [4] for sparse matrices.

3.2 Misfit exchange

In extended QR algorithms the shift information is encoded in the misfit. In floating point arithmetic this shift information is perturbed during the misfit chasing: the shifts get blurred. In some cases, e.g., in multishift implementations, the effect of shift blurring is so extreme that no useful shift information reaches the bottom of the matrix and the convergence stalls (see [34]).

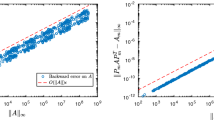
In the extended K-Hamiltonian QR algorithm we have an additional possible source of perturbations: the misfit exchange. To examine this we have generated random extended K-Hamiltonian Hessenberg matrices of dimension $200\times 200$ ($n=100$), with a random position vector, complex random G and R, and random rotations $Q_i$ with real sines. We set $G=G_r+G_r^H$, where $G_r$ is a random complex matrix, generated with Matlab’s randn function. The matrix R is taken from the QR-decomposition of a randomly generated matrix.³ The tests have been executed for various sizes of f and we also tested it for a tiny $r_{100,100}$. Table 1 depicts the absolute distance between the actual shift and the shift retrieved from the misfit at four occasions: immediately after the misfit is generated, before the exchange, after the exchange, and at the end of the chasing procedure.

We can deduce from Table 1 that the perturbation created by exchanging the misfits is not particularly larger than the perturbations introduced during the chasing. Moreover, considering tiny f and $r_{100,100}$ appears not significant for the accuracy of the shift.

Table 1 Perturbation of the shift during misfit chasing and misfit exchange, for different choices of $f:=f_{1n}$ and $r_{100,100}$

3.3 Iterations per eigenvalue and accuracy

In this section we examine the average number of iterations and the accuracy of the Hamiltonian QR algorithm. The matrices have been generated as in Sect. 3.2 and we have tested the algorithm for $n=25, 50, 100$, and 200. For each n we have generated 250 extended K-Hamiltonian Hessenberg matrices. The pattern of the rotations in the extended Hamiltonian Hessenberg matrix has been generated randomly. Since every QR step chases two misfits, the number of chases is twice the number of iterations. Dividing the number of chases by the matrix size 2n we get an average of the number of misfit chases that are required for each eigenvalue; this value equals the number of iterations divided by n. Table 2 shows that the average number of iterations is approximately 4.6 for these examples. The table further shows the relative backward error based on the computed K-Hamiltonian Schur decomposition $V^{H}TV$, where T is a K-Hamiltonian upper triangular matrix and V the accumulation of the performed K-symplectic similarity transformations, namely

$$\begin{aligned} \text {Relative backward error}\ =\frac{\parallel \!H - V^{H}TV\!\parallel _{2}}{\parallel \!H\!\parallel _{2}}. \end{aligned}$$

3.4 The effect of different position vectors

Different position vectors can influence the convergence behavior of the extended QR algorithm [30]. We test this fact here for the extended K-Hamiltonian QR algorithm and execute similar experiments as in [30].

Table 2 Average number of iterations per eigenvalue for a random Hamiltonian matrix of size 2n

We generate a K-Hamiltonian Hessenberg matrix with $\hbox {rank }F=1$ and prescribed eigenvalues $1+k/n$ and $-1-k/n$ for $k=1,\ldots ,n$. To do so, we use an inverse eigenvalue problem based on rotation chasing described in [24] that we have adapted to the K-Hamiltonian setting. We arrange the eigenvalues on the diagonal obeying the K-Hamiltonian structure, then apply a real rotation to the rows n and $n+1$ to bring F to rank 1. Finally, we apply the inverse eigenvalue code based on [24]. The result is a K-Hamiltonian Hessenberg matrix. Now we apply a random unitary K-symplectic matrix, $\left[ {\begin{matrix} Q &{} 0 \\ 0 &{}\Phi Q\Phi \end{matrix}}\right]$, to H and reduce the resulting matrix back to extended K-Hamiltonian Hessenberg form [15]. Thus, we have generated an extended K-Hamiltonian Hessenberg matrix with eigenvalues close to a desired distribution. Unfortunately the inverse eigenvalue problem perturbs the eigenvalues by about $10^{-12}$. Hence, we use the relative backward error of the Schur decomposition as accuracy measure and not a forward error such as the distance to the given eigenvalues.

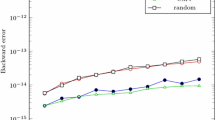
In Fig. 1 the relative backward error (solid line) and the number of iterations divided by n (dashed line) are plotted. We observe that the shape does not influence the relative backward error of the Schur decomposition. However, the Hessenberg and the inverse Hessenberg shape require significant less iterations than the CMV and the random shape. The inverse Hessenberg shape is slightly below 3 iterations per eigenvalue. Next, we have tested the extended Hamiltonian QR algorithm for the eigenvalue distributions $\pm k/n$, for $k=1,\ldots ,n$, see Fig. 2, and $\pm n/k$, for $k=1,\ldots ,n$, see Fig. 3: the results are very similar.

We find it surprising that the inverse Hessenberg shape always requires the least number of iterations. This is not in accordance with the observation for extended QR algorithms on general matrices: in [30] the inverse Hessenberg pattern performed worse than the standard Hessenberg pattern when the eigenvalues were distributed as in Fig. 3. A better understanding of how a particular chosen shape influences the convergences behavior in the K-Hamiltonian setting deserves further investigations.

Fig. 1

Relative backward error (left scale, solid line) and number of iterations (right scale, dashed line) for different shapes for eigenvalues ($1+k/n$ and $-1-k/n$ for $k=1,\ldots ,n$)

Fig. 2

Relative backward error (left scale, solid line) and number of iterations (right scale, dashed line) for different shapes for eigenvalues ($\pm k/n$, for $k=1,\ldots ,n$)

Fig. 3

Relative backward error (left scale, solid line) and number of iterations (right scale, dashed line) for different shapes for eigenvalues ( $\pm n/k$, for $k=1,\ldots ,n$)

Table 3 Number of iterations per eigenvalue (# it./n), relative backward error for the reduction to extended Hamiltonian Hessenberg form ($\rho _{\text {red}}$) and for the computation of the Hamiltonian Schur form ($\rho _{\text {QR}}$) for CAREX examples 14 and 18 and different patterns

3.5 CAREX

We test the reduction to extended Hamiltonian Hessenberg form and the computation of the Hamiltonian Schur form for two examples, Example 14 and Example 18, from the benchmark collection CAREX for continuous algebraic Riccati equations [6]. The other examples are either very small ($n=2$), have $\hbox {rank }F>1$, or are already almost in Hamiltonian Schur form. The examples from CAREX are parameter dependent; we used the standard parameter setting.

The results are shown in Table 3, there $\rho _{\text {red}}$ is the relative backward error for the reduction to extended Hamiltonian Hessenberg form and $\rho _{\text {QR}}$ the relative backward error of the Hamiltonian Schur form computed by the extended Hamiltonian QR algorithm. If we compare the different shapes, then we see the same picture as in the tests above: the inverse Hessenberg shape needs the least iterations followed by the Hessenberg shape for Example 18. Example 14 is arguably too small to draw conclusions from the iterations per eigenvalue.

4 Conclusions and future work

We have presented a new structure preserving algorithm for computing the Hamiltonian Schur form of an extended Hamiltonian Hessenberg matrix. The numerical experiments performed so far have confirmed the validity of our approach.

The numerical experiments are based on a simple single shift implementation. We are convinced that including well-known features, such as, aggressive early deflation [9, 25], multishift or multibulge steps with blocking [10, 19, 31], and changing to a higher order programming language, such as Fortran, would significantly improve the speed of the algorithm. For real Hamiltonian matrices it is also relevant to perform the QR iterations in real arithmetic to preserve the eigenvalue symmetry with respect to the real axis. This requires a double shift version of the algorithm which is more complicated than the single shift case and could be a subject of future research.