A flow mechanism for layering in a heterogeneous porous medium

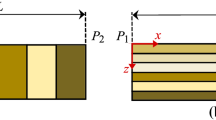
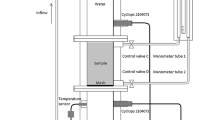
Abstract

The flow of a particle fluid mixture through a heterogeneous permeable material is studied with a view to obtaining characteristic fingerprints for the structures that such flows may exhibit. This flow has a variable density and behaves as a compressible fluid, with the compressibility derived from the variations of the local field variables. Both pressure-sensitive or speed-fluctuation-dependent rheologies are studied in the steady state and a speed-fluctuation-dependent material is studied in a time-dependent analysis. The salient findings are that for a pressure-sensitive material structures normal to the mean flow direction are obtained. For the speed-fluctuation-dependent rheology, the pressure structures are normal to the mean flow, whereas the density structures are aligned with the flow (fingering).

Appendix

Mathematical analysis of time-dependent flow equations

The basic equation is Eq. (20) as shown below.

$$ G\frac{{\partial k^{ + } {\left( x \right)}}} {{\partial x_{1} }} + \bar{k}\nabla ^{2} p^{ + } {\left( {x,t} \right)} = - B\frac{{\bar{v}}} {{\bar{\rho }}}{\left[ {G\frac{{\partial k^{ + } {\left( x \right)}}} {{\partial x_{1} }} + \bar{k}\frac{{\partial ^{2} p^{ + } {\left( {x,t} \right)}}} {{\partial x^{2}_{1} }}} \right]} - B\frac{{\bar{k}}} {{\bar{\rho }}}\frac{{\partial ^{2} p^{ + } {\left( {x,t} \right)}}} {{\partial x_{1} \partial t}} $$

This equation contains both time-dependent and time-independent terms. The solution for p ⁺(x,t), therefore, also includes time-dependent and time-independent parts. The latter are of most interest here. They are easily identified and the resulting equation for the explicitly time-dependent reads.

$$ \bar{\rho }\nabla ^{2} p^{ + } {\left( {x,t} \right)} + B\bar{v}\frac{{\partial ^{2} p^{ + } {\left( {x,t} \right)}}} {{\partial x^{2}_{1} }} + B\frac{{\partial ^{2} p^{ + } {\left( {x,t} \right)}}} {{\partial x_{1} \partial t}} = 0 $$

(A1)

This equation is essentially linear and contains the averaged material properties and velocity only. It may be analysed by means of a spatial Fourier transform and a temporal Laplace transform. The latter transform is denoted by a ^~ and the Laplace frequency is called s.

$$ B\frac{\partial } {{\partial x_{1} }}{\left( {s\tilde{p}{\left( x \right)} - p^{ + } (x,0)} \right)} + {\left( {B\bar{v} + 1} \right)}\frac{{\partial ^{2} \tilde{p}(x)}} {{\partial x^{2}_{1} }} + \bar{\rho }\frac{{\partial ^{2} \tilde{p}(x)}} {{\partial x^{2}_{2} }} = 0 $$

(A2)

The Fourier transform with wave vector λ is denoted by a ^. Its definition and inverse are given here by Eqs. (10) and (11).

Equation (A2) in the Fourier domain takes the form

$$ i\lambda _{1} B{\left[ {s\hat{\tilde{p}}{\left( \lambda \right)} - \hat{p}{\left( {\lambda ,0} \right)}} \right]} - \lambda ^{2}_{1} {\left( {B\bar{v} + 1} \right)}\hat{\tilde{p}}(\lambda ) - \lambda ^{2}_{2} \bar{\rho }\hat{\tilde{p}}(\lambda ) = 0 $$

(A3)

This algebraic equation is readily solved for $\hat{\tilde{p}}$ to yield

$$ \hat{\tilde{p}}{\left( {\lambda ,s} \right)} = - \frac{{i\lambda _{1} B\hat{p}{\left( {\lambda ,0} \right)}}} {{\lambda ^{2}_{1} {\left( {B\bar{v} + 1} \right)} + \lambda ^{2}_{2} \bar{\rho } - i\lambda _{1} Bs}} $$

(A4)

The pressure pulse is introduced at t=0 and its form is such that it is localised and has a convenient mathematical form, in order to preserve as much analyticity as possible.

Doing the inverse Laplace transform leaves

$$ \hat{p}{\left( {\lambda ,t} \right)} = \hat{p}{\left( {\lambda ,0} \right)}{\left[ { - i\sin (at) + \cos (at)} \right]} $$

(A5)

where $a = \lambda _{1} {\left( {B\bar{v} + 1} \right)}/B + \lambda ^{2}_{2} \bar{\rho }/{\left( {\lambda _{1} B} \right)}$.

The inverse Fourier transform is now carried out. It is convenient to work with positive integration variables only; straightforward algebra yields

$$ \begin{aligned} p{\left( {x,t} \right)} = \frac{2} {{{\left( {2\pi } \right)}^{2} }}{\int\limits_0^\infty {d\lambda _{1} {\int\limits_0^\infty {d\lambda _{2} \hat{p}{\left( {\lambda ,0} \right)}\left[ {\cos {\left( {\lambda _{1} x + \lambda _{2} y - \frac{{B\bar{v} + 1}} {B}\lambda _{1} t - \frac{{\bar{\rho }\lambda ^{2}_{2} t}} {{B\lambda _{1} }}} \right)}} \right.} }} } + & \\ \left. { + \cos {\left( {\lambda _{1} x - \lambda _{2} y - \frac{{B\bar{v} + 1}} {B}\lambda _{1} t - \frac{{\bar{\rho }\lambda ^{2}_{2} t}} {{B\lambda _{1} }}} \right)}} \right]. & \\ \end{aligned} $$

(A6)

The function $\hat{p}{\left( {\lambda ,0} \right)}$ is specified. A convenient form is $\hat{p}{\left( {\lambda ,0} \right)} = P_{0} e^{{ - \lambda \mu }}$. The parameter μ has the dimension of a length and indicates the spatial extent of the initial disturbance. This corresponds to a representation in the spatial domain of the form

$$ \begin{aligned} p^{ + } {\left( {x,0} \right)} = \frac{{P_{0} }} {{{\left( {2\pi } \right)}^{2} }}{\int\limits_0^{2\pi } {d\phi {\int\limits_0^\infty {d\lambda \lambda e^{{ - \lambda \mu }} e^{{i\lambda {\left( {x_{1} \cos \phi + x_{2} \sin \phi } \right)}}} } }} } = & \\ \frac{{P_{0} }} {{2\pi }}{\int\limits_0^\infty {d\lambda \lambda e^{{ - \lambda \mu }} J_{0} {\left( {\lambda r} \right)}} } = \frac{{P_{0} }} {{2\pi }}\frac{1} {{{\sqrt {r^{2} + \mu ^{2} } }}}. & \\ \end{aligned} $$

(A7)

The integration over λ₂ in Eq. (A6) is scaled by introducing a change in variable λ₂=λ₁0. Equation (A6) then takes the form

$$ \begin{aligned} p{\left( {x,t} \right)} = \frac{{2P_{0} }} {{{\left( {2\pi } \right)}^{2} }}{\int\limits_0^\infty {d\lambda _{1} {\int\limits_0^\infty {d\theta \lambda _{1} e^{{ - \lambda _{1} \mu {\sqrt {1 + \theta ^{2} } }}} \left[ {\cos {\left( {\lambda _{1} x + \theta \lambda _{1} y - \frac{{B\bar{v} + 1}} {B}\lambda _{1} t - \frac{{\bar{\rho }t}} {B}\lambda _{1} \theta ^{2} } \right)}} \right.} }} } + & \\ \left. { + \cos {\left( {\lambda _{1} x - \theta \lambda _{1} y - \frac{{B\bar{v} + 1}} {B}\lambda _{1} t - \frac{{\bar{\rho }t}} {B}\lambda _{1} \theta ^{2} } \right)}} \right]. & \\ \end{aligned} $$

(A8)

The integral over λ₁ is elementary. The result is

$$ p{\left( {x,t} \right)} = - \frac{{2P_{0} }} {{{\left( {2\pi } \right)}^{2} }}{\int\limits_0^\infty {d\theta {\left[ {\frac{{S^{2}_{1} - \mu ^{2} {\left( {\theta ^{2} + 1} \right)}}} {{{\left( {S^{2}_{1} - \mu ^{2} {\left( {\theta ^{2} + 1} \right)}^{2} } \right)}^{2} }} + \frac{{S^{2}_{2} - \mu ^{2} {\left( {\theta ^{2} + 1} \right)}}} {{{\left( {S^{2}_{2} - \mu ^{2} {\left( {\theta ^{2} + 1} \right)}^{2} } \right)}^{2} }}} \right]}} } $$

(A9)

where $S_{{1,2}} = x_{1} \pm \theta x_{2} - \frac{{B\bar{v} + 1}} {B}t - \frac{{\bar{\rho }t}} {B}\theta ^{2}$.

Despite its apparent simple form, the integral over θ cannot be done analytically, except for t=0; it is easily done numerically however.