Abstract
In the era of the metaverse, self-avatars are gaining popularity, as they can enhance presence and provide embodiment when a user is immersed in Virtual Reality. They are also very important in collaborative Virtual Reality to improve communication through gestures. Whether we are using a complex motion capture solution or a few trackers with inverse kinematics (IK), it is essential to have a good match in size between the avatar and the user, as otherwise mismatches in self-avatar posture could be noticeable for the user. To achieve such a correct match in dimensions, a manual process is often required, with the need for a second person to take measurements of body limbs and introduce them into the system. This process can be time-consuming, and prone to errors. In this paper, we propose an automatic measuring method that simply requires the user to do a small set of exercises while wearing a Head-Mounted Display (HMD), two hand controllers, and three trackers. Our work provides an affordable and quick method to automatically extract user measurements and adjust the virtual humanoid skeleton to the exact dimensions. Our results show that our method can reduce the misalignment produced by the IK system when compared to other solutions that simply apply a uniform scaling to an avatar based on the height of the HMD, and make assumptions about the locations of joints with respect to the trackers.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Head-Mounted Displays (HMD) offer an immersive experience that can greatly enhance presence in a virtual environment. The main problem when experiencing a virtual environment through this technology is that users cannot see their own bodies when they look down or try to interact with the environment. This creates the strange feeling of being a floating head without a body, which, in addition to being disturbing, can introduce other undesirable effects, such as increased motion sickness, or lack of correct perception of distances and sizes.
For a long time, this issue has been mostly ignored in applications such as video games, architecture visualization, education, and training. One of the reasons is that having a realistic-looking body following the user’s movement requires very costly equipment, such as full-body scanners and high-end motion capture systems.
As HMDs are becoming more affordable and more users have access to this technology, it is necessary to explore solutions to introduce low-cost self-avatars into any virtual environment. Currently, there are many tools that can be used to rapidly create avatars such as MakeHumanFootnote 1 and CharacterGenerator.Footnote 2 They produce humanoid meshes, each with a biped skeleton and a rig, ready to be animated in any engine.
In order to have an avatar that accurately follows the user’s movements, it is necessary to track the user and apply real-time inverse kinematics (IK) to animate the avatar in the virtual environment. There are current solutions for real-time IK that can be used in a game engine. The problem, however, is that an IK solver will not provide accurate movement unless the avatar proportions correspond to those of the user. In case of a dimension mismatch, there will be visible discrepancies such as the avatar’s knees being bent while the user is standing upright, or the controllers appearing to fly away from the avatar’s hand (see Fig. 1). This lack of adjustment is especially problematic when having a self-avatar because humans are very aware of their own body position; any mismatch with the avatar can be easily noticeable. For this reason, most high-quality mocap systems, such as Xsens, and several IK solutions for game engines, require the user to manually measure the length of their limbs and enter the information into the system in order to adjust the self-avatar skeleton correctly.
In this paper, we present a method to fit an avatar to the dimensions of a user rapidly. We use the HTC VIVE Head-Mounted Display (HMD), with two VIVE wand controllers (one for each hand), and three additional VIVE trackers, attached with straps to the user’s waist and feet. The user needs to follow a simple sequence of movements to capture the exact location of relevant joints and lengths of limbs. Once the avatar has been adjusted, we can animate it in real time using only those six trackers. The main advantage of this system is that the user can easily and quickly set up the avatar adjustment without any external assistance, using low-cost technology.
The contribution of this paper consists of a low-cost and easy-to-setup system that could be incorporated into any VR application where self-avatars are needed, without needing external assistance. Our results show that our method can quantitatively reduce the misalignment produced by the IK solution when compared to an avatar with a uniform scaling based on the user height. Participants experience higher embodiment and were less aware of pose artifacts when using our fitted avatar instead of a uniform scaling, but only when the initial avatar proportions differed from the user’s proportions.
2 Related work
2.1 Motion capture
High-end solutions for mocap include camera-based systems such as Vicon, or inertial-based systems such as Xsens. There are also lower-cost solutions based on RGB cameras (Mehta et al. 2020; Shi et al. 2020), or depth cameras (Wei and Zhang 2012). However, the use of external cameras requires the user to stay within the field of view of the cameras, which can be challenging when the user is immersed in a Head-Mounted Display. Most HMDs nowadays provide at least two controllers to interact with the virtual world. These devices provide the position and orientation of the head and hands of the user, which can be used to animate the upper body of an avatar. In the case of HTC VIVE, Zeng et al. (2022) include a few additional trackers, which, combined with an IK solver, can provide full self-avatar movement. They uniformly adjust the avatar’s size in accordance with the user’s height, and thus assume that the avatar always has the same ratios between bone lengths as the user. Therefore, their solution does not consider having a variety of body proportions as in our work. We refer to the survey by Aristidou et al. (2018) for an extensive survey on IK solutions.
There are currently several options to carry out IK using a few HTC VIVE trackers. Unity’s built-in IK solves each limb individually using four end-effectors (feet and hands), so two controllers and two HTC trackers can be used to animate the self-avatar, while the HMD orientation is applied to the avatar head. Unfortunately, this solution is very limited, as it simplifies the IK solution to each limb, and will not adjust the back of the avatar to lean toward the tracker if it becomes out of reach. Also, since there is no end-effector for the avatar’s head, if the person bends forward, the avatar will simply rotate its head accordingly, but will not modify its back joins. FinalIKFootnote 3 computes joint rotations for all body parts to minimize the distance between the end-effectors and the HTC trackers, and includes an IK handler for the head which provides torso rotations and bending. However, it is not easy to assign trackers to end-effectors, and the fixed offsets applied between them result in incorrect alignments with the user, thus leading to large errors in body rotations and the overall positioning of the skeleton.
2.2 Character generation
There are currently many tools to generate avatars, such as MakeHuman or Autodesk Character Generator. These tools allow the user to tune different parameters to generate avatars of different heights, sizes, and proportions. However, once an avatar has been built and imported to a game engine, it cannot be changed any further, and thus it is not possible to adjust its dimensions to those of the real user.
High-quality characters that perfectly match a user’s size and appearance, can be created with expensive 3D scanners (Thaler et al. 2018), which are not accessible to the general public. And even if the external dimensions of the avatar are a perfect match, it is still impossible to have good correspondence with the inner skeleton, because this information cannot be captured with such technology.
The Virtual Caliper (Pujades et al. 2019) presented an easy-to-use framework to rapidly generate avatars that fit the shape of the user. They use the HTC VIVE wand controllers to take measurements of the user, and then they verify that they are linearly related to 3D body shapes from the SMPL body model (Loper et al. 2015). But even if the size of the avatar is correct in terms of the width of arms, legs, torso, etc., it does not guarantee that the positions of the avatar’s joints match those of the user, and this has a direct impact on achieving realistic positioning of limbs during motion. The most noticeable one is typically the shoulder location since it affects both the distance that our hand can reach, and how the arm bends.
Regardless of the technology used to generate the avatars, the problem of finding a good adjustment between the trackers and the avatar skeleton remains. A wrong mismatch may not be crucial when avatars are being used as characters that we interact with in Virtual Reality (VR), but in the case of self-avatars, even the smallest misalignment turns into an incorrect body position for the avatar that our proprioceptive system can detect.
2.3 Embodiment
Having a self-avatar in VR can induce a sense of embodiment that makes the user feel as if the virtual avatar was their own body. Embodiment requires correct tracking of the participant to animate the virtual avatar (Slater et al. 1995), and synchronized movements (Gonzalez-Francoand Lanier 2017).
Kilteni et al. (2012) described the sense of embodiment (SoE) as the extent a participant feels the virtual body is their own. They propose to divide the SoE into three subcomponents that can be measured through questionnaires: sense of self-location (being inside a virtual body), sense of agency (being in control of the virtual body movements), and sense of ownership (appearance of the virtual body representing the user).
Several aspects need to be taken into account to achieve embodiment, such as appearance, visuotactile stimuli, point of view, and virtual body movements. Maselli and Slater (2013) showed that first-person perspective over a virtual body is essential for evoking the illusion of body ownership, even without visuotactile or sensorimotor cues.
Embodiment has been proven to be essential to enhance user experience (UX) and has implications for the way the user perceives the virtual environment and experiences presence. For example, Mohler et al. (2010) showed that having a self-avatar can improve distance judgment when observing a virtual environment with an HMD. This is crucial for VR applications in architecture, where the user needs to have a reliable representation of the space. In a later experiment, which portrayed Lenin giving a speech to Red Army recruits in Moscow, Slater et al. (2018) showed that presence was greatest when a participant was embodied as Lenin or as part of the audience rather than observing the same scene from a third-person point of view. Unlike Freud’s experiment by Osimo et al. (2015), in which the whole body was tracked, when embodied as Lenin, only the head was tracked in real time. The movements of the virtual hands were prerecorded and participants noticed a lack of synchronization. Though they got a lower result in ownership, the SoE scores were still high. An interesting observation from this study is that when the participants noted the lack of synchrony with the hands, they attempted to match their movements to the Lenin virtual body.
Gonzalez-Franco et al. (2020) also examined the participants’ behavior when observing asynchronous visual feedback. If there is a drift between the self-avatar and the physical body, the participants tend to fill the gap and reduce the offset. The authors call this the self-avatar follower effect and emerge from the brain’s need to solve sensory conflicts. The higher the sense of ownership, the higher the need to reduce the offset.
Recently there has been an increasing interest in using collaborative virtual environments as a working platform for different fields. In these types of applications, two or more participants share a virtual environment to perform a certain task (Frost and Warren 2000; Andujar et al. 2018). These applications can greatly benefit from having virtual avatars to enhance nonverbal communication.
Ponton et al. (2022) presented a framework to compute exact offsets between six trackers located on the user body and the joints of its avatar. They observed that computing exact offsets, as opposed to default fixed ones, would improve the self-avatar movements leading to higher SoE. However, their avatars were simply adjusted in height to the user by applying a uniform scaling, which could not solve problems regarding the correct positioning of end-effectors (for example the hands) when animating the self-avatars.
When having a small number of trackers, it is challenging to provide full-body animation, and thus it is common to visualize only a part of the body (e.g., head and hands or upper body). The type of avatar visualization preferred by the user may depend on the type of task (Pastel et al. 2020) and also on the quality of the animations provided by the tracking system (Yun et al. 2023). In our work we developed a method to enhance the animation of full-body avatars to be used in immersive VR regardless of task requirements.
3 Avatar fitting framework
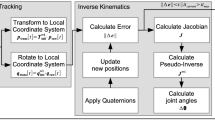
Our framework provides a pipeline to create fitted avatars to the specific dimensions of the user. To achieve this, the user needs three HTC trackers attached to the feet and back, an HMD, and a controller in each hand (see Fig. 2 left). Note that we locate the feet trackers on the user’s feet as opposed to the ankle, since this allows us to have full control of the feet orientation to simulate, for example, walking on tiptoes. The user can see the virtual representation of those devices in the virtual world with a reflection in a virtual mirror (see Fig. 2 right). Next, the user follows a short sequence of exercises to automatically extract the location and dimensions of their joints and limbs (this set of exercises is explained in Sects. 3.2.1 and 3.2.2 and it takes around 60 s for the user to complete.). Once the avatar has been adjusted to the user’s dimensions, the final step consists of walking inside a virtual body that matches the user’s dimensions, making a T-pose inside the avatar and pressing a trigger to compute the exact offset between trackers and joints (Ponton et al. 2022). Figure 3 shows the steps required to set up the avatar with the correct user skeleton dimensions.
Framework setup. After choosing an avatar, the user stands on a T-pose to automatically identify the trackers and extract some measurements (Step 1). Next, the user follows a short sequence of exercises to automatically extract the location and dimensions of the user’s joints and limbs (Step 2). Then the avatar skeleton is resized to match the user dimensions (Step 3). Finally, the user has to place himself inside the visualized avatar in order to compute the exact offsets between the avatar joints and the user trackers (Step 4)
For the rest of the paper we will use the following notation:
-
\(\textbf{p}(T_i)\): position of the tracking device T for body part i.
-
\(\textbf{p}(J_i)\): position of the joint J for body part i.
-
\(\textbf{h}(T_i)\): height of the tracking device T for body part i.
-
\(\textbf{h}(J_i)\): height of the joint J for body part i.
3.1 Step 1: Automatic tracker identification
The first step consists of identifying and assigning each tracker to a body part. To determine where each device is placed on the user’s body, we ask the user to stand on a T-pose, facing a virtual mirror. From the position of the six trackers, we compute a plane using a least square error fitting approach. The HMD forward vector and the vertical axis of the world are used to create a coordinate system to identify left and right devices. Then, knowing the relative positions of the trackers in this coordinate system, we uniquely identify each tracker to a body joint (see Algorithm 1 for details). Finally, we store the height of those trackers needed for the skeleton adjustment in Step 3, as \(\textbf{h}(T_i)\), where \(i \in \{\text {HMD }, root, Rfoot, Lfoot\}\).

3.2 Step 2: Joint locations and limb dimensions
To fit an avatar to the user, it needs to be resized to match the user’s dimensions, but more importantly, we need to correctly locate the relevant joint rotations. In our experience, most of the accuracy problems, that we observe when animating self-avatars with IK, are due to not having the joints’ location correctly positioned with respect to the trackers. This can be frequently observed in the hand position, which appears to correctly hold the controller for certain arm positions but not for others, such as when the user moves the arms toward the sky. This happens because even though the size of the avatar’s arm may be correct, the location of the avatar’s shoulder joint is not. It is important to note that even if the avatar dimensions were correct, it will still not improve all possible movements, because the avatar’s skeleton is a simplified version of a human one. So, for example, a person can move the shoulders a bit front or back, whereas a typical avatar skeleton does not have this degree of freedom as some bones are not represented (or are not animated by the IK solvers). Our method expects a humanoid avatar with at least three joints per limb, two in the spine and one for the neck.
In order to correctly map the user’s body to the avatar, we need to infer the location of some of the user’s body joints. Those locations can also be used to determine several body measures. The length of some parts of the body can be extracted directly from the distance between trackers, or from the height of the trackers when the participant is standing in T-pose. Since we want to keep the required number of trackers low, it is not possible to track every single joint individually. Therefore, starting with the basic configuration of HMD, two controllers and three VIVE trackers, we designed a set of exercises to infer the location of non-tracked joints. Since several body joints are centers of rotation when moving a limb, we can compute their location by calculating the center of a point cloud forming a sphere, which is captured by the tracker located at the end of the limb. We use a least squares solution for estimating the average center of rotation and the radius of the sphere (Gamage and Lasenby 2002). This method is used for the left and right arm and for the neck, as follows:
-
Shoulders: position of the center of rotation \(\textbf{p}(C_{shoulder})\) of the point cloud obtained with the controllers tip positions \(\textbf{p}(T_{wrist})\) when moving it with the straight arms.
-
Arm length: radius of the fitted sphere obtained from the hand controllers, which corresponds to the distance:
$$\begin{aligned} \mathbf {L_{arm}} = distance(\textbf{p}(C_{shoulder}),\;\textbf{p}(T_{wrist})) \end{aligned}$$ -
Neck: position of the center of rotation \(\textbf{p}(C_{neck})\) of the point cloud obtained with the HMD tracker positions \(\textbf{p}(T_{\text {HMD }})\) when performing head rotations.
In our experience, those body parts can be easily rotated while keeping the rest of the body still in a T-pose. Other parts of the body, such as the legs, are difficult to rotate while keeping the rest of the body still, and thus this method cannot be applied.
Other dimensions can be easily extracted from trackers, since they are accurately located on the user’s body, or using the computed shoulders from the fitted sphere:
-
Leg length—difference in height between the root and the feet trackers:
$$\begin{aligned} \mathbf {L_{leg}} = \textbf{h}(T_{root})-\frac{\textbf{h}(T_{Lfoot})+\textbf{h}(T_{Rfoot})}{2} \end{aligned}$$ -
Torso length (up to shoulders)—difference in height between the computed shoulders and the root tracker:
$$\begin{aligned} \mathbf {L_{torso}} = \textbf{h}(C_{shoulder})-\textbf{h}(T_{root}) \end{aligned}$$ -
Shoulder to neck length—difference in height between the computed shoulder and the computed neck: the computed shoulders and the root tracker:
$$\begin{aligned} \mathbf {L_{neck}} = \textbf{h}(C_{neck})-\textbf{h}(C_{shoulder}) \end{aligned}$$ -
Neck to eyes length—difference in height between the HMD and the computed neck:
$$\begin{aligned} \mathbf {L_{eyes}} = \textbf{h}(T_{\text {HMD }})-\textbf{h}(C_{neck}) \end{aligned}$$
3.2.1 Shoulder joint extraction
Shoulders joint position \(\textbf{p}(C_{shoulders})\) is obtained by asking the user to do an exercise that consists of moving the arms in circles while keeping the arm as straight as possible. Both arms have to be moved synchronously to reduce the noise caused by other moving body parts (for example, a small movement of the spine will affect both shoulders’ positions simultaneously by drifting slightly). Figure 4 shows the arm exercise movement with blue arrows. As the participant performs this exercise, we capture the point cloud of controller positions which will approximate the shape of a sphere (see Fig. 5). A least squares solution is used to estimate the center of rotation (Gamage and Lasenby 2002).
To ensure high precision when fitting the spheres, the algorithm has to satisfy two conditions to be completed (1) a minimum number of n points, further than d centimeters apart from each other, and (2) a convergence threshold \(\tau\). See Algorithm 2 for details. After experimental training of the system, we set the following values \(n=70\), \(d=5\;\)cm, and \(\tau = 2\;\)cm.

We considered using this method also for the wrists, but it was very hard for the participants to keep their arms completely still while rotating only the hands. Therefore, the wrist location is extracted directly from the controllers. To do so, the participant is asked to hold the controller with the tip touching their wrist (see Fig. 6 left).
On the left, the center of rotation of the head (blue dot) is computed from the head exercise to determine the neck joint position. This exercise consists of moving the head upwards and sideways as shown with the blue arrows. On the right, the orange dot shows the point of minimum displacement over the plane which traverses the HMD when the head rotates. This point is used to bend the spine with forward kinematics (Color figure online)
3.2.2 Neck joint computation and head center estimation
Similarly, the neck position \(\textbf{p}(C_{neck})\) can be computed as the center of rotation of the head. Therefore, we perform a fitting sphere algorithm using the HMD position and ask the participant to perform an exercise that consists of moving the head up/down, left/right, and rotating in circles. Following the same algorithm as for the shoulders, we empirically found the following parameter values: \(n=60\), \(d=1.5\;\)cm, and \(\tau = 2\;\)cm.
Since Unity’s built-in IK does not provide an end-effector for the head, the self-avatar cannot perform movements such as bending forward or to the sides to reach for objects. Unfortunately, this affects the overall movements of the avatar, thus limiting the benefit of our fitted avatars. We thus included a forward kinematic method to compute the angle of rotation of the spine given by the root position \(\textbf{p}(T_{root})\) and the head’s center position \(\textbf{p}(C_{head})\) (Ponton et al. 2022). The head position is a fixed point with respect to the HMD local coordinate system that has the least displacement when the user rotates the head wearing the HMD (Fig. 6 shows the movement of the head during the exercise with blue arrows). This point is computed during the neck exercise using the following method:
-
1.
Define a 2D grid of cells located over the plane defined by the forward \({\hat{\textbf{f}}}\) and right \({\hat{\textbf{r}}}\) unit vectors of the HMD local coordinate system: \(\textbf{G}\) of resolution \(n\times m\) with cells of size s.
-
2.
Initialize the position of all cells on this grid in global coordinates as \(\textbf{G}^0_{ij}\)
-
3.
While the head is moving (\(t\in [1,t_{end}]\)) to perform the fitting sphere algorithm, compute for each cell of the grid the displacement between the current global position and its initial position, and keep track of the maximum displacement for each grid cell during the iterative head rotations.
$$\begin{aligned} \textbf{M}^t_{ij}=\max (\textbf{G}^t_{ij}-\textbf{G}^0_{ij},\; \textbf{M}^{t-1}_{ij}),\; t \in [1,t_{end}] \, \wedge \, \, \forall i,j \in \{n\times m\} \end{aligned}$$ -
4.
When the head exercise finishes, we search for the cell with the smallest maximum displacement and keep its position as the center of the head. This point suffers the minimum displacement when the user rotates the head without bending the back.
$$\begin{aligned} (i^*, j^*)&= \arg \min (\textbf{M}^{t_{end}}_{ij}),\; \forall i,j \in \{n\times m\} \\ \textbf{p}(C_{head})&= \textbf{p}(T_{\text {HMD }}) + s(-{\hat{\textbf{f}}})i^* + s{\hat{\textbf{r}}}\left( j^* - \frac{m}{2}\right) \end{aligned}$$
3.3 Step 3: Skeleton adjustment
Once we know the distances between the required body joints, and their heights with respect to the floor, we can adjust the avatar’s limbs’ dimensions. In order to have a virtual avatar matching the user’s body as close as possible, we follow a two-pass process: (1) uniform avatar scaling, and (2) skeleton tuning.
3.3.1 Uniform avatar scaling
A uniform scaling is applied based on the user’s height to preserve the avatar’s proportions. Uniformly scaling the avatar ensures that we do not excessively deform its mesh in the skeleton tuning step. Since the participant’s height is unknown, the scaling is done by computing the ratio between the participant’s eyes height \(\textbf{h}(T_{\text {HMD }})\) and the avatar’s eye height \(\textbf{h}(J_{eye})\). Note that the uniform scaling step only guarantees a good match between the avatar and the user height. Any other limb dimension will depend on how close the user proportions were to the chosen avatar.
3.3.2 Skeleton tuning
To resize the avatar bones based on the user’s limb measurements, we focus on five bone chains: the two arm chains, the two leg chains and the spine chain. Our method stretches or shrinks the length of each of those chains while keeping the ratios between the bones’ length for each chain. Please refer to Fig. 7 for the naming convention of the bones.
Leg chain: The avatar’s lower and upper leg bones are resized according to the participant’s leg height \(\mathbf {L_{leg}}\).
Arm chain: Similarly, the lower and upper arm bones are resized to match the participant’s arm length \(\mathbf {L_{arm}}\).
Spine chain: First we adjust the shoulder width and then the spine length. The avatar’s shoulder width is adjusted by scaling along the axis defined by the vector connecting both shoulder joints:
According to this axis, shoulder joints are positioned so that they are at a distance d apart. The distance d is given by the distance between the shoulders’ centers of rotation from Step 2:
Then we need to resize the vertical dimension of the bone chain comprising the avatar’s spine, chest and upper chest bones, to match the avatar’s shoulder height with the height of the shoulder centers of rotation \(\textbf{h}(C_{Lshoulder})\) and \(\textbf{h}(C_{Rshoulder})\).
The final step is to adjust the avatar’s neck height to match the user’s neck height. We first used the computed \(\textbf{p}(C_{neck})\) as the neck of the avatar. Unfortunately given the oversimplification of the neck bones in the avatar, there is not an exact correspondence for the joint \(\textbf{p}(J_{neck})\). Assigning the avatar’s neck joint to the participant’s computed neck would lead to an avatar with an extremely long neck from a perceptual point of view, whereas using the avatar’s head bone would cause the opposite visual effect (a very short neck). So using our current avatar, the real participant’s neck would be in between those two avatar joints, and thus, to keep the perceptual plausibility of the model, we resize those two bones to adjust the avatar’s eye level with the participant’s eye height. This solution offers a good compromise between the height of the avatar and the participant, while keeping a pleasant resizing of the avatar’s head and neck. If the avatar model had more bones defined at the neck, it would be better to match the neck at its exact center of rotation. The center of the head computed in Sect. 3.2.2 is not needed for the skeleton adjustment, but for the forward kinematics needed to bend the spine.
3.4 Step 4: Walk-in-avatar for interactive coupling
For the final step, a virtual avatar with the correct user’s dimensions is rendered in T-pose in front of a virtual mirror. The user can also see the virtual trackers attached to their real body. With this visual aid, the user is asked to walk into the avatar and stay in T-pose making sure that the virtual trackers appear located over the avatar, and press a trigger when there is a correct coupling between their body and the avatar.
This step computes the exact vector offset between the position of the lower back tracker and the avatar’s root as well as their initial rotations. The same computation is performed for the feet trackers and the avatar’s ankles. Those exact offsets will be used for the avatar animation, and are key to having a correct pose for the avatar at all times, as shown in Fig. 8 (details of the computation can be found in Ponton et al. 2022).
This step cannot be further automatized, because, without a correct overlaying of the user and the avatar, it would not be possible to compute the exact offset between the avatar’s hip and the root tracker located on the participant’s lower back. Most methods assume that the avatar hip corresponds to the root trackers, which leads to severe problems with the avatar’s legs dimensions and results in avatars that may appear to walk on tiptoes or to have their knees always bent (Fig. 1).
Therefore, the user is responsible for positioning themselves so that the back tracker appears to be correctly aligned with the avatar’s back, and similarly, feet trackers are correctly located over the avatar’s feet. To help the user with this self-positioning, the user can use the mirror as a visual aid to get a front view, and a screen that shows the top view of the avatar simultaneously. The user can see the virtual avatar simultaneously with the virtual trackers. Any misalignment in this step (for instance the user locating himself/herself 10 cm in front of the virtual body) will obviously affect the offsets between the user body and its self-avatar (for example, when extending the arms forward, they would appear shorter and give the impression of not reaching the virtual controllers) see Fig. 9 top for a visual example of such situation. The result of a correct alignment within the fitted avatar is shown in Fig. 9 bottom.
4 Experimental evaluation
The goal of the evaluation is twofold: firstly we want to quantify the error in accuracy that appears when animating an avatar that has been obtained with uniform scaling as opposed to the fitted avatar provided by our framework (Accuracy evaluation); and secondly, we want to evaluate whether this error is perceptually noticeable for the user and whether or not it affects the sense of embodiment (SoE) (Perceptual evaluation). Figure 10 shows the pipeline for the experimental evaluation.
User study organization. The user study consists of two evaluations: Accuracy Evaluation, which consists of a quantitative statistical evaluation of a set of metrics; and a Perceptual Evaluation, which consists of a user perceptual evaluation of the SoE. The orange blocks are part of the immersive VR experience (Color figure online)
4.1 Data preparation: avatar types
To take into account the variability of human body dimensions, we build a database with several body proportions. We created five male and five female avatars with different body proportions (i.e., skeleton configurations) as shown in Fig. 11. All avatars were created with MakeHuman (which allows fine-tuning of body dimensions) and rigged with Mixamo.Footnote 4
The five avatars (for each gender) created for the Accuracy evaluation are:
-
\(\textbf{SA}\): Standard Avatar with a shoulder width and ratio between lower and upper body following the golden ratio defined by Da Vinci in the Vitruvian Man (Magazù et al. 2019; Sheppard 2013).
-
\(\mathbf {N_SA}\): Narrow Shoulder Avatar, obtained by reducing the shoulder width of SA.
-
\(\mathbf {W_SA}\): Wide Shoulder Avatar, obtained by increasing the shoulder width of SA.
-
\(\mathbf {L_LA}\): Long Leg Avatar, obtained by increasing the leg length of SA, while keeping the same height (thus reducing the upper body length).
-
\(\mathbf {S_LA}\): Short Leg Avatar, obtained by decreasing the leg length of SA, while keeping the same height (thus increasing the upper body length).
Each avatar type will then be tested with the two scaling methods, (Uniform vs. Fitted) thus leading to 10 conditions. The Uniform method consists of exclusively applying a uniform scaling as described in Sect. 3.3.1, whereas the Fitted method consists of applying the complete framework as described in Sect. 3.
The avatars DB used in the Accuracy Evaluation experiment. Using the MakeHuman framework we built four different avatar proportions for male and female from a standard body proportions avatar (SA). The red squares show the difference in width/length between different body parts of the avatars (Color figure online)
To reduce the number of avatars for the Perceptual Evaluation, we used only two avatar configurations: the Standard Avatar, SA, and a Different Avatar, DA. We generate DA for each participant by choosing the combination of shoulder width and upper/lower body ratio that provides the avatar with the proportions being as different as possible from the participant. The combination of those two avatar types (\(\textbf{SA}\) vs. \(\textbf{DA}\)) with the two scaling methods (Uniform vs. Fitted), led to 4 conditions (see Fig. 10).
4.2 Experimental design
Participants are first briefed about the steps of the experiment and the total duration. After signing a consent form and filling out a demographics questionnaire, they put on the three VIVE trackers, the HTC Vive PRO wireless HMD and take one controller in each hand. During the Avatar fitting step, the participant performs the exercises as shown in a video that is displayed within the immersive experience. During this part of the experiment, our pipeline computes the participant’s skeleton dimensions. The participant then performs an accuracy evaluation followed by a perceptual evaluation.
4.2.1 Accuracy evaluation
During this phase, the user performs a sequence of exercises while the pipeline extracts data to perform quantitative measurements for the five avatar conditions (\(\textbf{SA}\), \(\mathbf {L_LA}\), \(\mathbf {S_LA}\), \(\mathbf {W_SA}\), \(\mathbf {N_SA}\)), as shown in Fig. 11, and the two scaling methods Uniform and Fitted, thus testing 10 conditions. The avatar is not rendered while performing these exercises. The first exercise (ArmsMovExercise) consists of doing circles in the air with the arms completely stretched while standing in T-pose (similar to the first exercise of the Avatar Fitting setup described in Sect. 3.2.1). The second exercise (LegsMovExercise), consists of positioning the arms in an akimbo position while doing squats.
When performing these exercises, the application records all the positions and orientations of the trackers and controllers. Then we use this data to simulate the animation of each of the 10 avatar conditions while computing the offsets between each tracker and its corresponding joint. This allows us to use the exact same movements performed by the user for all five avatars. Section 5.1 explains the results obtained through a statistical analysis of the recorded data.
4.2.2 Perceptual evaluation
For the Perceptual evaluation, participants are embodied in four avatar conditions (\(\mathbf {SA_{Fitted}}\), \(\mathbf {SA_{Uniform}}\), \(\mathbf {DA_{Fitted}}\), \(\mathbf {DA_{Uniform}}\)) to evaluate the SoE based on avatar type and scaling method. For each condition, users carry out a few exercises and then fill out an embodiment questionnaire. Conditions were shown to participants following a balanced Latin square order to avoid learning/fatigue influencing the results. After the experiment, users can share their personal experiences by writing in a document.
To induce embodiment we ask participants to perform a sequence of steps, the first one involves moving freely in front of a mirror to observe how the virtual avatar mimics their movements (Attention & Motion phase) (Roth and Latoschik 2020). For the second step, we ask the participants to play a simple basketball game (Motion only phase), which consists of grasping a colored ball using the right/left controller depending on the color of the ball, and dropping it inside a basket that appears randomly located within the virtual room. The purpose of this game is to make sure that participants pay attention to the avatar’s arms. After approximately five minutes, the final step (Attention only phase) consists of asking the users to touch different parts of their body following our instructions. Finally, users answer an embodiment questionnaire, while still being immersed in the virtual experience.
The following questionnaire was answered by participants after experiencing each condition (using a Likert scale from 1 to 7), which is based on the proposed questionnaire by Roth and Latoschik (2020). It includes three main aspects of Embodiment (change, ownership and agency):
- CH1:
-
“I felt like the form or appearance of my own body had changed.”
- CH2:
-
“I felt like the size (height) of my own body had changed.”
- CH3:
-
“I felt like the width of my own body had changed.”
- CH4:
-
“I felt like the size of my own arms had changed.”
- CH5:
-
“I felt like the size of my own legs had changed.”
- OW1:
-
“It felt like the virtual body was my body.”
- OW2:
-
“It felt like the virtual body parts were my body parts.”
- OW3:
-
“The virtual body felt like a human body.”
- AG1:
-
“The movements of the virtual body felt like they were my movements.”
- AG2:
-
“I felt like I was controlling the movements of the virtual body.”
- AG3:
-
“I felt like I was causing the movements of the virtual body.”
Change is the average of questions \(\{CH1,CH2,CH3,CH4,CH5\}\), Ownership is the average of questions \(\{OW1,OW2,OW3\}\), and Agency is the average of questions \(\{AG1,AG2,AG3\}\).
Some authors have included Change as a way of evaluating whether participants accept a different avatar as their own for studying the Proteus effect (Roth and Latoschik 2020), or for experiments where they want to put participants in another person’s shoes (e.g., to study racial or gender issues). This is not the case in our work, because all avatars look similar but with small differences in body proportions. Our goal is not to test if participants accept the body change, but whether participants notice differences in size between their real body and the avatar. Therefore, we define:
Small values of change prove a good avatar adjustment that is perceived as positive by the participant. Participants will score high when they consider that the virtual avatar has different proportions than them, thus implying a negative embodiment and the other way around.
4.3 Apparatus and participants
The software has been developed in Unity, and an HTC Vive PRO HMD wireless, two controllers and three trackers are used. A total of 27 subjects participated in the experiments, 17 males and 10 females, ranging between 18 and 62 years old. Participants were selected from our academic institution, encompassing faculty members, staff personnel, and master’s/Ph.D. students, as well as individuals enrolled in higher education nondegree certificate (HNC) programs. \(42\%\) of the participants were familiar with VR applications. All participants exhibited unrestricted mobility without any observable movement impairments. For each embodiment question, subjects were asked to give a score on a Likert scale with 1 meaning very low and 7 very high. Our study used a within-subject design, so participants experienced all the conditions which followed a randomized design based on balanced Latin squares. Statistical analysis was performed with R. This study complies with UPC ethics requirements and regulations.
5 Results
We analyzed all the data collected in the experiments to assess how the scaling method used (Uniform vs. our Fitted method) and the different avatar types, influenced the accuracy of the avatar joints positioning with respect to the trackers (Sect. 5.1) and the Sense of Embodiment (SoE) (Sect. 5.2).
5.1 Accuracy evaluation
To evaluate quantitatively the quality of the avatar in terms of how well the virtual avatar was adjusted to the real body, we defined some anchor points in the avatar skeleton and measured their distance to the controllers while the participant performed the two exercises described in Sect. 4.2.1.
During the first exercise (ArmsMovExercise), we measured the distance between each hand controller and the corresponding wrist joint of the avatar. If the avatar’s shoulder position and arm length are correct, then, this distance should be small and stable while performing the exercises, otherwise, this distance grows when the controller is located in positions that are not reachable due to the inaccurate avatar size.
In the second exercise (LegsMovExercise), consisting in doing squats, the user places the controllers approximately at the top of each leg. During this exercise, we took two measures: the distance between each controller and the corresponding hip joint of the avatar, and also the knee angle. Therefore, the measurements taken in both exercises were:
-
\(Hand_{Dist}\): Distance between each controller and the corresponding wrist joint.
-
\(Leg_{Dist}\): Distance between each controller and the corresponding hip joint while being in the akimbo position.
-
\(Knee_{Ang}\): Angle of each knee joint.
Our hypotheses for the accuracy evaluation were:
- H1:
-
Avatar hand position would be more accurate using the Fitted scaling method.
- H2:
-
Avatar legs pose would be better adjusted using the Fitted scaling method.
A two-way repeated measures ANOVA (mixed model with the participant as a random effect) was performed using as response each distance variable (\(Hand_{Dist}\) and \(Leg_{Dist}\)). The considered fixed factors were the scaling method (Uniform vs. Fitted) and avatar type (5 levels: SA, \(\mathbf {N_SA}\), \(\mathbf {W_SA}\), \(\mathbf {L_LA}\), \(\mathbf {S_LA}\)). Since different avatars are used for each gender, we performed the statistical analysis separately. Due to the presence of some outliers, the normality assumption was not thoroughly fulfilled, and thus, apart from the parametric approach we also applied the nonparametric aligned rank transform (ART) ANOVA approach (Wobbrock et al. 2011). We remark that both, the parametric and nonparametric approach, yielded the same results in terms of statistical significance; see “Appendix ” for a detailed description of the complete statistical analysis including the nonparametric results in Tables 2 and 3.
Herein, we will mainly illustrate results with the classic repeated ANOVA analysis using the distances variable (\(Hand_{Dist}\) and \(Leg_{Dist}\)) .Footnote 5
For each gender, the repeated ANOVA analysis of the \(Hand_{Dist}\), yielded as significant the main factor method (Uniform vs Fitted), the avatar type (5 models) and also their interaction (all p values \(< 0.0001\)); see Table 2 (top) in “Appendix ”. Additionally, we computed Cohen’s f effect sizes (Cohen 1988), which can be interpreted as very small (\(f \ge 0.01\)), small (\(f \ge 0.2\)), medium (\(f \ge 0.5\)), large (\(f \ge 0.8\)), very large (\(f \ge 1.2\)), or huge (\(f \ge 2.0\)) (Sawilowsky 2009). Regarding male participants, we observed a huge effect on the scaling method factor (\(f=2.30\)), a large effect on the interaction between factors (\(f=0.84\)), and a small effect for the avatar type factor (\(f=0.43\)). When examining female participans, we observed a large effect in all cases: scaling method (\(f=1.11\)), avatar type (\(f=0.92\)), and interaction (\(f=0.84\)). Figure 12 (left) also suggests that participants’ bodies were better adjusted when using the Fitted method.
Post hoc comparisons were carried out, and the obtained effects (Uniform vs. Fitted) for all the avatar type configurations are displayed in Fig. 12 (right) and in Table 3 (top). There is only one configuration (\(S_LA\)-female) where the Uniform method outperforms the fitted method, but, as observed in the forest plot, the effect value is very close to 0.0. The effect size for \(Hand_{Dist}\) ranges from 4.0 cm. to 14.0 cm for males and from 2.6 to 8.0 cm for females. These results support our hypothesis H1.
Regarding the \(Leg_{Dist}\) variable, which is in charge of analyzing the low body when performing the LegsMovExercise, we also found as significant the main factor method (Uniform vs Fitted), the avatar type (5 models) and also their interaction (all p-values \(< 0.0001\)); see Table 2 (bottom). When examining the male participants, we found a large effect size for the interaction between factors (\(f=1.0\)), and medium effects for the scaling method factor (\(f=0.77\)) and avatar type factor (\(f=0.66\)). When considering female participants, we observed a large effect for the scaling method factor (\(f=1.07\)), and medium effects for both the avatar type factor (\(f=0.55\)) and the interaction between the two factors (\(f=0.72\)). Corresponding post hoc comparison effects are displayed in Fig. 15 (right) and in Table 3 (bottom). These results support our hypothesis H2.
Additionally, we analyze the knee angle variable, and we observed some interesting behavior. Figure 13 shows the time plot of the knee angle when a participant is performing the exercise for the different avatar types under both scaling methods. If we observe the variability in the knee angle value, it is larger when using the Uniform method than when using the Fitted method. This is due to the fact that when using the Uniform scaling, there is a larger variability in leg length, and thus in the correspondence between the user and the avatar knee bending. In contrast, for the Fitted method, where the avatars’ leg length is the same as the user, then for all avatars we observe a similar knee angle during the squatting exercise. This result also supports H2.
5.2 Perceptual evaluation
We carried out the perceptual experiment described in Sect. 4.2.2 to study the impact of avatar type and scaling method on the SoE. Answers from the questionnaires were structured into three groups (ResizeAccuracy, Ownership, and Agency). Our main hypothesis was:
- H3:
-
Embodiment ratings would be higher when using a Fitted avatar.
A two-way ANOVA was performed to analyze the effect of avatar type (\(\textbf{SA}\) vs. \(\textbf{DA}\)) and scaling method (Fitted vs. Uniform) on SoE. Results were not statistically significant and not shown.
Since, as planned in our experiment, \(\textbf{DA}\) had been chosen as the most different avatar in terms of body proportions to each participant, we then restricted our statistical analysis to this condition. The corresponding paired t-test was performed comparing the scaling method for the SoE (and its components). The obtained results were statistically significant (higher) only for SoE and the Ownership component; (SoE: \(t = 2.34, df = 21, p < 0.029\); Ownership: \(t = 2.72, df = 21, p < 0.013\)). The normality assumption for the differences was verified by the Shapiro–Wilk normality test (SoE: \(W = 0.94, p <0.17\); Ownership: \(W = 0.95, p <0.36\)). Figure 14 includes the summary of this analysis (the \(\mathbf {DA_{Uniform}}\) vs. the \(\mathbf {DA_{Fitted}}\)). These results support our hypothesis H3.
To further justify the necessity of our Fitted scaling method, when restricting the statistical analysis to the Uniform scaling method, a paired t-test was performed comparing the ResizeAccuracy in both conditions: \(\textbf{SA}\) versus \(\textbf{DA}\). The obtained results showed significant and higher values for \(\textbf{SA}\) (\(t =2.54, df = 21, p < 0.02\)). This indicates that when participants use an avatar with very different proportions to them, they will notice the mismatch in dimensions if a uniform scaling is applied. The normality condition of the differences was tested using the Shapiro–Wilk normality test: \(W =0.94, p <0.208\).
6 Discusion
The presented framework provides an automatic fitting of avatars to better match the user dimensions. We have tested both quantitatively and qualitatively our results to evaluate the quality of our method when compared against a simple uniform scaling based on user height.
Regarding the positioning of the avatar hand with respect to the controllers, our results show that using our Fitted scaling method the accuracy is improved regardless of the avatar type being used. Similarly, the accuracy of the distance between the avatar hip joint and the controllers in the akimbo position was also improved when using our Fitted scaling method.
It is interesting to highlight that the participants’ leg movement when looking at the knee angle, was well reproduced for all the avatar types regardless of the scaling methods. The reason for this is that our exact offset computation between the back tracker and the hip joint, allows the avatar pose to be correctly initialized regardless of the avatar type or scaling method (i.e., they are all initially in a T-pose). Then when the participant bends the knees, all avatars behave correctly by bending the knees in sync with the user, and when the participant straightens the leg, all avatars return to a straight leg position. The errors in leg size simply produce differences in the knee angle which can be observed in a quantitative evaluation, but are not perceivable by the user. Ideally, we would like to compare the knee angle against the real participant knee angle, but this was beyond the scope of this project since it would require specific hardware to measure it automatically (for example a full motion capture suit).
When we only apply uniform scaling, it is likely that the arm’s length does not match the user dimensions (since the ratios of the initial avatar remain unchanged). Therefore, for those avatars with shorter arms, the user will observe that the avatar stays in T-pose for a few seconds after the user starts moving the arms toward the body. This happened to most of our avatars, since the stretching needed to adjust the length of the user’s arm was positive (see Fig. 16). To measure the correctness of the elbow angle, we should also compare it against ground truth data from a full motion capture suit.
The perceptual study shows that when using the Uniform scaling method, users perceived the Resize Accuracy as higher for \(\textbf{SA}\) than for \(\textbf{DA}\). This implies that uniform scaling will lead to perceivable size errors if the avatar used has different proportions from the user. Regarding ownership and SoE for the DA (avatar with proportions different to the user), participants rated significantly higher scores for the Fitted scaling than for Uniform. Therefore, our method to compute fitted avatars can reduce the perceivable errors that appear when using an avatar that is not proportionally similar to the user, and lead to higher Ownership and SoE. However, the qualitative differences perceived by the participants were smaller than the quantitative differences. The reasons for this could be twofold (1) the tasks that the users had to perform did not require careful positioning of the body limbs or accurate manipulation of virtual objects, and thus errors in the positioning of the end-effectors were not highly noticeable for the users, and (2) our current method correctly resizes each limb, but in some cases artifacts may appear with the mesh resizing or the rigging, thus leading to other noticeable visual artifacts that may impair the benefits of having accurate skeleton dimensions.
It is important to note that our method assumes that the user can follow correctly the rules and exercises indicated, since the quality of the results depends to a large extent on how well the user is following those exercises. During our experiments, all participants performed the exercises correctly and the automatic extraction was quickly achieved. However, people with limited mobility may not be able to perform the arm or head rotation correctly and thus the automatic extraction of joints could be less accurate.
7 Conclusion
We have presented a method to automatically compute accurate body dimensions and joint locations from a user, to then adjust the skeleton of a self-avatar to minimize the errors in poses and position of end-effectors during animation. By computing the most accurate location of joints and replicating their positions correctly in the avatar, our framework is able to improve the final body positions calculated by an inverse kinematics (IK) solver. Our method improves the final accuracy regardless of the avatar type being used, and thus facilitates the use of avatars for immersive VR applications using low-cost setups, such as an HTC VIVE system with three additional trackers.
Data availability
Availability of data and materials data and related materials are available upon reasonable request to the corresponding author.
Notes
MakeHuman: http://www.makehumancommunity.org.
Autodesk Character Generator: https://charactergenerator.autodesk.com.
RootMotion’s FinalIK: http://root-motion.com/.
Adobe Mixamo: https://www.mixamo.com.
Distance variables (\(Hand_{Dist}\) and \(Leg_{Dist}\)) stand for left body side. Results corresponding to the right side were similar in terms of statistical significance and thus omitted here.
Distance variables (\(Hand_{Dist}\) and \(Leg_{Dist}\)) stand for left body side. Results corresponding to the right body side were similar in terms of statistical significance and were thus omitted here.
References
Andujar C, Brunet P, Buxareu J, Fons J, Laguarda N, Pascual J, Pelechano N (2018) VR-assisted architectural design in a heritage site: the Sagrada Família case study. In: EUROGRAPHICS workshop on graphics and cultural heritage (EG GCH). https://doi.org/10.2312/gch.20181340. Eurographics
Aristidou A, Lasenby J, Chrysanthou Y, Shamir A (2018) Inverse kinematics techniques in computer graphics: a survey. Comput Graph Forum 37:35–58. https://doi.org/10.1111/cgf.13310
Cohen J (1988) Statistical power analysis for the behavioral sciences. Lawrence Erlbaum Associates, New York. https://doi.org/10.1016/C2013-0-10517-X
Frost P, Warren P (2000) Virtual reality used in a collaborative architectural design process. In: IEEE international conference on information visualization, 2000. Proceedings. IEEE, pp 568–573. https://doi.org/10.1109/IV.2000.859814
Gamage SSHU, Lasenby J (2002) New least squares solutions for estimating the average centre of rotation and the axis of rotation. J Biomech 35(1):87–93. https://doi.org/10.1016/S0021-9290(01)00160-9
Gonzalez-Franco M, Lanier J (2017) Model of illusions and virtual reality. Front Psychol 8:1125. https://doi.org/10.3389/fpsyg.2017.01125
Gonzalez-Franco M, Cohn B, Ofek E, Burin D, Maselli A (2020) The self-avatar follower effect in virtual reality. In: 2020 IEEE conference on virtual reality and 3D user interfaces (VR). IEEE, pp 18–25. https://doi.org/10.1109/VR46266.2020.1580500165557
Kilteni K, Groten R, Slater M (2012) The sense of embodiment in virtual reality. Presence Teleoperators Virtual Environ 21(4):373–387. https://doi.org/10.1162/PRES_a_00124
Loper M, Mahmood N, Romero J, Pons-Moll G, Black MJ (2015) SMPL: a skinned multi-person linear model. ACM Trans Graph (Proc SIGGRAPH Asia) 34(6):248–124816. https://doi.org/10.1145/2816795.2818013
Magazù S, Coletta N, Migliardo F (2019) The Vitruvian Man of Leonardo da Vinci as a representation of an operational approach to knowledge. Found Sci 24:751–773. https://doi.org/10.1007/s10699-019-09616-5
Maselli A, Slater M (2013) The building blocks of the full body ownership illusion. Front Hum Neurosci 7:83. https://doi.org/10.3389/fnhum.2013.00083
Mehta D, Sotnychenko O, Mueller F, Xu W, Elgharib M, Fua P, Seidel H-P, Rhodin H, Pons-Moll G (2020) Theobalt C Xnect: real-time multi-person 3D motion capture with a single RGB camera. ACM Trans Graph 39(4):82:1. https://doi.org/10.1145/3386569.3392410
Mohler BJ, Creem-Regehr SH, Thompson WB, Bülthoff HH (2010) The effect of viewing a self-avatar on distance judgments in an HMD-based virtual environment. Presence Teleoperators Virtual Environ 19(3):230–242. https://doi.org/10.1162/pres.19.3.230
Osimo SA, Pizarro R, Spanlang B, Slater M (2015) Conversations between self and self as Sigmund Freud: a virtual body ownership paradigm for self counselling. Sci Rep 5:13899. https://doi.org/10.1038/srep13899
Pastel S, Chen C-H, Petri K, Witte K (2020) Effects of body visualization on performance in head-mounted display virtual reality. PLoS ONE 15(9):0239226. https://doi.org/10.1371/journal.pone.0239226
Ponton J.L, Monclús E, Pelechano N (2022) AvatarGo: plug and play self-avatars for VR. In: Eurographics 2022: short papers. The Eurographics Association, Reims, France, pp 77–80. https://doi.org/10.2312/egs.20221037
Pujades S, Mohler B, Thaler A, Tesch J, Mahmood N, Hesse N, Bülthoff HH, Black MJ (2019) The virtual caliper: rapid creation of metrically accurate avatars from 3D measurements. IEEE Trans Vis Comput Graph. https://doi.org/10.1109/TVCG.2019.2898748
Roth D, Latoschik ME (2020) Construction of the virtual embodiment questionnaire (VEQ). IEEE Trans Vis Comput Graph 26(12):3546–3556. https://doi.org/10.1109/TVCG.2020.3023603
Sawilowsky SS (2009) New effect size rules of thumb. J Mod Appl Stat Methods 8:26. https://doi.org/10.22237/jmasm/1257035100
Sheppard J (2013) Anatomy: a complete guide for artists. Courier Corporation, New York
Shi M, Aberman K, Aristidou A, Komura T, Lischinski D, Cohen-Or D, Chen B (2020) MotioNet: 3D human motion reconstruction from monocular video with skeleton consistency. ACM Trans Graph 40(1):1–15. https://doi.org/10.1145/3407659
Slater M, Usoh M, Steed A (1995) Taking steps: the influence of a walking technique on presence in virtual reality. ACM Trans Comput Hum Interact 2(3):201–219. https://doi.org/10.1145/210079.210084
Slater M, Navarro X, Valenzuela J, Oliva R, Beacco A, Thorn J, Watson Z (2018) Virtually being Lenin enhances presence and engagement in a scene from the Russian revolution. Front Robot AI 5:91. https://doi.org/10.3389/frobt.2018.00091
Thaler A, Piryankova I, Stefanucci JK, Pujades S, de la Rosa S, Streuber S, Romero J, Black MJ, Mohler BJ (2018) Visual perception and evaluation of photo-realistic self-avatars from 3D body scans in males and females. Front ICT. https://doi.org/10.3389/fict.2018.00018
Wei X, Zhang P, Chai J (2012) Accurate realtime full-body motion capture using a single depth camera. ACM Trans Graph 31(6):1–12. https://doi.org/10.1145/2366145.2366207
Wobbrock JO, Findlater L, Gergle D, Higgins JJ (2011) The aligned rank transform for nonparametric factorial analyses using only ANOVA procedures, pp 143–146. https://doi.org/10.1145/1978942.1978963
Yun H, Ponton J.L, Andujar C, Pelechano N (2023) Animation fidelity in self-avatars: impact on user performance and sense of agency. In: 2023 IEEE conference virtual reality and 3D user interfaces (VR). IEEE, Shanghai, China, pp 286–296. https://doi.org/10.1109/VR55154.2023.00044
Zeng Q, Zheng G, Liu Q (2022) PE-DLS: a novel method for performing real-time full-body motion reconstruction in VR based on vive trackers. Virtual Real. https://doi.org/10.1007/s10055-022-00635-5
Acknowledgements
This work was funded by the Spanish Ministry of Science and Innovation (PID2021-122136OB-C21). Jose Luis Ponton was also funded by the Spanish Ministry of Universities (FPU21/01927).
Funding
Open Access funding provided thanks to the CRUE-CSIC agreement with Springer Nature.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors have no relevant financial or nonfinancial interests to disclose
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Supplementary file 1 (mp4 81381 KB)
Appendix: complementary statistical analysis results
Appendix: complementary statistical analysis results
This appendix collects all statistical results of the Accuracy Evaluation experiment described in Sect. 5.1. Table 1 shows the descriptive analysis of the distance–response variables (\(Hand_{Dist}\) and \(Leg_{Dist}\)).Footnote 6
Figure 12 and Fig. 15 (top) show that the bodies of the participants were better adjusted when using the Fitted scaling method. A further justification of the differences observed can be explained when analyzing the stretching performed in each avatar. We have collected the avatar stretching (scaling) applied for all five avatars and for all participants; see Fig. 16. We observed that the avatars for male participants were always larger than the avatars for female participants, being \(N_{SA}\) the avatar with the greatest scaling (arms were scaled 23 cm, as opposed to an average of 12 cm for the rest of the avatars) (Tables 2, 3).
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ponton, J.L., Ceballos, V., Acosta, L. et al. Fitted avatars: automatic skeleton adjustment for self-avatars in virtual reality. Virtual Reality 27, 2541–2560 (2023). https://doi.org/10.1007/s10055-023-00821-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10055-023-00821-z