Skip to main content
SpringerLink
Log in

Improving the non-extensive medical image segmentation based on Tsallis entropy

  • Theoretical Advances
  • Published:
Pattern Analysis and Applications Aims and scope Submit manuscript

Abstract

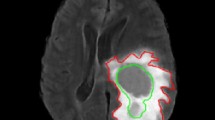
Thresholding techniques for image segmentation is one of the most popular approaches in Computational Vision systems. Recently, M. Albuquerque has proposed a thresholding method (Albuquerque et al. in Pattern Recognit Lett 25:1059–1065, 2004) based on the Tsallis entropy, which is a generalization of the traditional Shannon entropy through the introduction of an entropic parameter q. However, the solution may be very dependent on the q value and the development of an automatic approach to compute a suitable value for q remains also an open problem. In this paper, we propose a generalization of the Tsallis theory in order to improve the non-extensive segmentation method. Specifically, we work out over a suitable property of Tsallis theory, named the pseudo-additive property, which states the formalism to compute the whole entropy from two probability distributions given an unique q value. Our idea is to use the original M. Albuquerque’s algorithm to compute an initial threshold and then update the q value using the ratio of the areas observed in the image histogram for the background and foreground. The proposed technique is less sensitive to the q value and overcomes the M. Albuquerque and k-means algorithms, as we will demonstrate for both ultrasound breast cancer images and synthetic data.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

Notes

  1. We define the composed distribution, also called direct product of \(P = [p_1, \ldots, p_n]\) and \(Q = [q_1,\ldots, q_n], \) as \(P \ast Q =\{p_iq_j\}_{i,j},\) with \(1 \leq i \leq n\) and \(1 \leq j \leq m\)

References

  1. Aback T, Baris U, Sankur B (1997) The performance of thresholding algorithms for optical character recognition. In: International conference on document analysis recognition ICDAR’97, pp 697–700

  2. Albuquerque MP, Albuquerque MP, Esquef IA, Mello ARG (2004) Image thresholding using Tsallis entropy. Pattern Recognit Lett 25:1059–1065

    Article  Google Scholar 

  3. Bhanu B (1986) Automatic target recognition: state of art survey. IEEE Trans Aeroespacial Electron Syst AES-22: 364–379

    Google Scholar 

  4. Chen S, Lin W, Chen C (1992) Split-and-merge image segmentation based on localized feature analysis and statistical tests. CVGIP Graph Models Image Process 53(5):457–475

    Article  Google Scholar 

  5. Duda RO, Hart PE, Stork DG (2000) Pattern classification, 2nd edn. Wiley, New York

  6. Geman D, Geman S (1984) Stochastic relaxation, gibbs distribution and bayesian restoration of images. IEEE Trans Patterns Anal Mach Intell (PAMI) 6:721–741

    Article  Google Scholar 

  7. Giraldi GA, Oliveira AAF (1999) Dual-snake model in the framework of simplicial domain decomposition. In: Technical poster of international symposium on computer graphics, image processing and vision—SIBGRAPI’99, pp 103–106

  8. Giraldi GA, Schaefer L, Rodrigues PS (2000) Gradient vector flow models for boundary extraction in 2d images. In: Proceedings of the 8th international conference on computer graphics and image—IASTED CGIM 2005

  9. Giraldi GA, Strauss E, Oliveira AAF (2000) Boundary extraction approach based on multi-resolution methods and the t-snakes framework. In: Proceedings of the international symposium on computer graphics, image processing and vision—SIBGRAPI’00, Gramado, Rio GRande do Sul, Brazil

  10. Giraldi GA, Strauss E, Oliveira AAF (2000) A boundary extraction method based on dual-t-snakes and dynamic programming. In: Proceedings of the IEEE computer society conference on computer vision and pattern recognition, CVPR’2000

  11. Gonzalez RC, Woods RE (1992) Digital image processing. Addison-Wesley, Reading

  12. Jain AK, Murty MN, Flynn PJ (1999) Data clustering: a review. ACM Comput Surv 31(3):264–323

    Article  Google Scholar 

  13. Kamel M, Zhao A (1993) Extracting of binary character/graphics image from grayscale document images. Graph Models Image Process 55(3):203–217

    Article  Google Scholar 

  14. Kanungo T, Dom B, Niblack W, Steele D (1994) A fast algorithm for mdl-based multi-band image segmentation. In: Proceedings of IEEE conference on computer vision and pattern recognition, pp 609–616

  15. Kapur JN, Sahoo PK, Wong AKC (1985) A new method for gray-level picture thresholding using the entropy of the histogram. Comput Graph Image Process 29:273–285

    Article  Google Scholar 

  16. Pun T (1981) Entropic thresholding: a new approach. Comput Graph Image Process 16:210–239

    Article  Google Scholar 

  17. Rodrigues PS, Giraldi GA (2004) Parameter estimation with a bayesian network in medical image segmentation. In Proceeding of the 17th international conference of computer graphics and image—IASTED-CGIM, Kauai, Hawaii, USA, October 2004

  18. Rodrigues PS, Giraldi GA, Chang RF, Suri J (2006) Non-extensive entropy for cad systems of breast cancer images. In: IEEE Computer Society (ed) Proceedings of Brazilian symposium on computer graphics and image processing, Belo Horizonte, Brazil, pp 121–128

  19. Rodrigues PS, Giraldi GA, Suri J (2006) Object tracking combining Haudorff distance, HSV histogram and non-extensive entropy, vol 1, chap 15. Springer, New York

  20. Sahoo P, Soltani S, Wong A, Chen Y (1988) A survey of thresholding techniques. Comput Vis Graph Image Process 41(1):233–260

    Article  Google Scholar 

  21. Sezgin M, Sankur B (2001) Comparison of thresholding methods for non-destructive testing applications. In: International conference on image processing, IEEE ICIP’2001, pp 764–767

  22. Sezgin M, Sankur B (2004) Survey over image thresholding techniques and quantitative performance evaluation. J Eletron Imaging 13(1):146–165

    Article  Google Scholar 

  23. Sezgin M, Tasaltin R (2000) A new dichotomization technique to multilevel thresholding devoted to inspections. Pattern Recognit Lett 21:151–161

    Article  Google Scholar 

  24. Shannon C, Weaver W (1948) The mathematical theory of communication. University of Illinois Press, Urbana

    Google Scholar 

  25. Shapiro LG, Stockman GC (2001) Computer vision. Prentice Hall, Upper Saddle River

    Google Scholar 

  26. American Cancer Society (2004) Cancer facts & figures

  27. Tsallis C (1999) Nonextensive statistics: theoretical, experimental and computational evidences and connections. Braz J Phys 29(1):1–35

    Google Scholar 

  28. Tsallis C (2001) Nonextensive statistical mechanics and its applications. In: Series lecture notes in physics. Springer, Berlin. The bibliography of the subjects is regularly updated at http://tsallis.cat.cbpf.br/biblio.htm

Download references

Author information

Authors and Affiliations

  1. IAAA Group, University Center of FEI, São Paulo, Brazil

    Paulo S. Rodrigues

  2. Department of Computer Science, National Laboratory for Scientific Computing, Rio de Janeiro, Brazil

    Gilson A. Giraldi

Authors
  1. Paulo S. Rodrigues
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Gilson A. Giraldi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Paulo S. Rodrigues.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Rodrigues, P.S., Giraldi, G.A. Improving the non-extensive medical image segmentation based on Tsallis entropy. Pattern Anal Applic 14, 369–379 (2011). https://doi.org/10.1007/s10044-011-0225-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10044-011-0225-y

Keywords

Search

Navigation