1 Introduction

Handling and processing of granular materials is crucial to a wide range of industries. Many of these display difficult handling behavior, posing considerable challenges in the design and operation of processing plants. The scientific insight into mechanical behavior of granular materials facilitate optimization of conveying, handling and processing systems. The up to date theory of granular mechanics mainly considered bulk material as a monodisperse system, however most particle packings involved in industrial and natural processes are composed of particles of a broad range of particle sizes. Granular packings may be composed of one, two, three or more components. Binary mixtures represent the simplest case of polydisperse particulate systems which exhibit interesting and, in some cases, incomprehensive behavior. Understanding of such behavior could pave the way for a more rapid and accurate interpretation of effects observed in more complex packings of non-uniformly sized grains. It has been widely reported that a degree of particle polydispersity strongly affects packing density of granular mixtures [1–3] and arrangement of particles in the granular system [4]. Experimental [1, 2], theoretical [2–4] and numerical [5–8] studies have been conducted to determine packing density of particulate beds, which is of prime importance to scientists and engineers. The packing density of the granular system was found to be sensitive to mechanical and geometrical properties of particles (e.g. friction [9, 10] and the particle size ratio [1, 6, 11–14]), the degree of particle size heterogeneity [7] and the volume fraction of small particles [1–3, 6, 11, 15]. Mixing particles of various sizes with different volume fraction is a common way to increase the density of granular packings; however, an increase is observed in mixtures with the ratio of the diameter of large and small spheres far from unity. In close-packed binary mixtures, two basic types of particle arrangement are produced: tetrahedral and octahedral [16]. When the ratio of the diameter of small and large spheres is smaller than 0.225, small spheres may be trapped in the tetrahedron made with four large contacting spheres, which increases the density of the sample without a change in its volume. In the case of octahedron made by six identical spheres, a smaller sphere is trapped when the diameter of small particle is smaller than 0.414 of the diameter of the large sphere. For more homogeneous samples with size ratios close to unity packing density decreases [17].

McGeary [1] observed an increase in the packing density of binary mixtures comprising steel shots with size ratios varying from 1 to 19 with an increase in the number fraction of smaller particles up to above 60 %. A further increase in contribution of small shots in mixture resulted in a decrease in the packing density of samples. An experimental and theoretical study on the packing density of bidisperse mixtures with large size ratios, conducted by Rassously [2], confirmed findings of McGeary. The detailed characterization of packing structures of binary granular assemblies with different size ratios, conducted by Isola [4], indicated a strong influence of contribution of small particles in bedding on the radial distribution function (RDF), which provides information about the organization of particles in the system and long range interparticle correlations. As the packing density affects the number of contacts between particles, the number fraction of small particles in binary granular mixtures was also found to influence a coordination number [12, 18]. A numerical study prepared by Skrinjar and Larsson [12, 18] indicated that an increase in the number fraction of small particles in bimodal mixtures decreased the average coordination number and the presence of small particles in the sample reduced the coordination number, in comparison to the monodisperse packing. An experimental study conducted by Pinson et al. [19] on binary granular mixtures indicated that increasing the volume fraction of a small component increased contacts between small and large and small particles and decreased the small-to-large and large-to-large contacts. The changes were more significant for samples with a large size difference. Wiącek and Molenda [8] observed a decrease in the average coordination number with an increase in the degree of polydispersity of granular mixtures, due to the increase in the number of small particles percolating through the bedding. Dutt and Elliot [20] reported that the ratio of the smallest to the largest particle diameter in the granular packing must be larger than \(\big ( {\sqrt{2}-1} \big ) = 0.41\) to prevent grains from percolating through the sample.

Heterogeneity in the particle size strongly influences mechanical properties of the granular packings [1, 7, 8, 21, 22], which affects engineering processes to which materials are subjected. The degree of particle size heterogeneity determines the mechanical response of particulate systems to shear [22, 23] and compaction [3, 7, 8, 11, 12, 24, 25], and affects the flow of particle mixtures during mixing, discharge and other processes [14, 26]. Granular packings composed of non-uniformly sized grains reveal a high tendency towards strong segregation, which is undesirable for many solids handling processes [27–29]. Zhou et al. [3] reported strong dependence of the packing density, modulus of volume expansion and drag force of mixtures of different sized white aluminum oxide granules subjected to compression and drag experiments on the mass fractions. For each type of mixture, density and drag force approached a maximum when the mass percentage of larger particles was about 70–80 %, while modulus of volume expansion reached maximum at mass fraction of 30–50 %. The discrete element simulations of compaction of binary powder mixtures with size ratio higher than 4, conducted by Martin and Bouvart [11], have shown that bimodality of mixtures determined stiffness of mixtures affecting compaction and unloading stages.

The review of literature shows that extensive studies have been performed on the properties of bidisperse particulate packings; however, more detailed investigations addressing structural properties of mixtures with a various size ratio and a contribution of respective fractions to assembly, being of high interest to engineers and technological process designers, are still required. Thus, the objective of the presented project was to examine the dependence of structural properties of granular mixtures on the volume fraction of small particles in mixtures with particle size ratios larger than 0.4, wherein percolation of small spheres downwards between large grains does not take place. Experimental tests were completed by numerical simulations which allowed the author to analyze the transition from fully homogeneous monodisperse packings to heterogeneous systems with an increasing volume fraction of smaller particles. The application of the discrete element method (DEM) provided knowledge about structural properties of granular packings (the number of interparticle contacts and RDF), which so far remained unattainable using the experimental methods.

2 Materials and methods

2.1 Experimental method

The series of laboratory tests were conducted using an uniaxial compression apparatus of rectangular cross-section of 0.12 m \(\times \) 0.12 m and 0.1 m thick. The dimensions of the apparatus chamber were not smaller than 15 mean particle diameters which was found by the author as a representative elementary volume [30]. The elements of tester were machined from 6 mm thick galvanized steel, giving an essentially rigid boundary. The apparatus was equipped with steel top platen weighing 8.5 N.

The test materials were monodisperse and binary samples of steel beads. The binary mixtures were described by particle size ratio (g), defined as a diameter ratio of small \((D_{s})\) and large \((D_{l})\) beads, and volume fraction (f), defined as a volume ratio of smaller particles and the volume of all particles in bedding. In each binary assembly, one of the fractions comprised beads of the diameter of 8 mm and the second fraction was composed of steel beads with the diameter of 7.144, 6.35, 5.556, 4.762 or 4 mm. The size ratios of bidisperse mixtures ranged from 0.5 to 0.9. In this study, the size ratio was chosen not smaller than 0.4 to prevent small objects from percolating through bedding. In monodisperse packings containing the largest and the smallest beads, the number of elements varied from 3000 to 52,000, respectively. In bidisperse samples, the number of steel beads was determined by the volume fraction of smaller spheres, ranging from 0.2 to 0.8.

The steel beads were poured into the apparatus chamber with sprinkle filling. Next, samples were covered through the top platen which lay freely on the surface of the sample. The top platen exerted a pressure of 0.75 kPa on the uppermost beads, which equaled about 1 % of vertical pressure exerted by the sample on the bottom of the apparatus. Three replications were performed for each type of packing.

2.2 Numerical simulations

In this study, three-dimensional simulations were conducted using DEM. DEM [31], is a common numerical technique for the detailed investigation of mechanical behavior of granular systems. The simplified viscous-elastic non-linear Hertz–Mindlin contact model was used. The detection of contacts between particles is followed by calculating normal and tangential contact forces at each incremental time step, which is set small to allow one to assume a constancy of translational and rotational accelerations. The motion of each particle in the system is given by Newton’s equations. The integration of the equations of motion provides information regarding the particle’s position, velocity and resultant forces. The rigid particles are allowed to overlap locally at contact points using a soft contact approach. The detection of contacts between particles is followed by calculation of the normal \((F^{n})\) and tangential \((F^{t})\) contact forces at each incremental time step, given by:

$$\begin{aligned} F^{n}=k_n \delta _{n}^{\frac{3}{2}} , \end{aligned}$$
(1)
$$\begin{aligned} F^{t}=-k_{t} \delta _t , \end{aligned}$$
(2)

where \(k_{n}\) and \(k_{t}\) are normal and tangential stiffness coefficients, and \(\delta _{n}\) and \(\delta _{t}\) are normal and cumulative shear displacements. The stiffness coefficient may be expressed as:

$$\begin{aligned}&k_{n} =\frac{4}{3}Y^{*}\sqrt{R^{*}}, \end{aligned}$$
(3)
$$\begin{aligned}&k_{t} =8G^{*}\sqrt{R^{*}\delta _{n} }, \end{aligned}$$
(4)

where \(Y^{*}\) is an equivalent of Young’s modulus; \(R^{*}\) is an effective radius of contacting particles; and \(G^{*}\) is an equivalent shear modulus. The elastic constants, Young’s modulus Y and shear modulus G, are related to each other as follows:

$$\begin{aligned} G=\frac{E}{2\left( {1+\nu } \right) }, \end{aligned}$$
(5)

where \(\nu \) is a Poisson’s ratio.

The tangential contact force is limited by Coulomb’s friction law

$$\begin{aligned} F^{t}<\mu _s \left| {F^{n}} \right| , \end{aligned}$$
(6)

which assumes that particles slide over each other when the tangential force is at the limiting friction. The \(\mu _{s}\) is a coefficient of the static friction.

Numerical tests have been carried out using EDEM software [32]. The experimentally determined input parameters for steel beads and steel walls of the chamber are listed in Table 1.

Table 1 DEM input parameters
Full size table
Fig. 1
figure 1

The initial configuration of the binary mixture with the size ratio of 0.4 and the volume fraction of 0.4

Full size image
Fig. 2
figure 2

The evolution of the solid fraction versus the volume fraction of small particles in experimental (a) and numerical (b) binary mixtures with various size ratios

Full size image

The spherical particles with random initial coordinates were generated in the box 0.12 m wide, 0.06 m high and 0.1 m thick placed above the model chamber of the uniaxial compression apparatus. Spheres settled down onto the bottom of the box measuring 0.12 \(\times \) 0.12 \(\times \) 0.1 m under gravitational force (Fig. 1). Rigid and frictional walls did not deform under the applied load. As soon as a total kinetic energy of particles decreased below 10\(^{-5}\) J, which was considered an equilibrium state, spheres were compressed through the top cover of the chamber that moved vertically downwards at a constant velocity of 3 m/min. The maximum vertical force of 8.5 N exerted on the cover by uppermost particles was equaled to gravity of the top platen used in experimental tests. Three replicate tests were performed for each sample to verify the repeatability.

The simulations were conducted for monodisperse and binary samples comprising spheres with diameters of 8, 6.35 and 4.762 mm, analogical to ones examined in laboratory tests. Additionally, specimens composed of spheres with diameters of 8 and 3.175 mm were generated in simulations to study the effect of the volume fraction of small particles on structural properties of packings with size ratio of 0.4. The diameters of spheres varied within \(\pm \)2 % to simulate real steel beads and to prevent identical particles from rearranging themselves into a crystal-like formation.

Fig. 3
figure 3

The evolution of the coordination number (a) and the corrected coordination number (b) with the volume fraction of small particles in numerical binary mixtures with different size ratios

Full size image

3 Results

3.1 Solid fraction

Figure 2 shows the evolution of solid fraction (\(\varphi \)) with the volume fraction of small particles in physical and numerical mixtures with various particle size ratios. The solid fraction of a granular material is defined as the fraction of the sample volume filled by grains. The mean values are plotted with the error bars indicating \(\pm \) one standard deviation. Compared with monodisperse samples, in binary mixtures with size ratios smaller than 0.6 solid fractions were smaller, which was in agreement with results presented by Zhou et al. [3] and Jalali and Li [6]. In mixtures with the size ratio of 0.6 and 0.7, an increase in the solid fraction with an increase in f value up to 0.6 was observed, which was then followed by decrease in solid fraction at volume fraction of small elements of 0.8. A further decrease in the number of smaller particles in mixtures resulted in an increase in solid fractions which, finally, were the highest in monodisperse samples composed of small particles. The maximum \(\varphi \) value in packings with g value smaller than 0.7 occurred at the volume fraction of smaller beads of 0.6, which corroborated findings reported earlier by inter alia McGeary [1], Rassously [2], Jalali and Li [6]. In samples with the high particle size ratio, the solid fraction increased slightly in the whole range of f and no maximum in the value of the parameter was observed, which was in opposite to numerical predictions conducted by Jalali and Li [6]. These results indicate that above a certain value of the particle size ratio, the solid fraction of binary samples does not reach maximum. Solid fractions varied from 0.597 to 0.625 in physical samples which corroborated findings of, inter alia, Chen [33] and Francois et al. [34], EDEM Software [32] and Francois et al. [34], who reported that for randomly arranged spheres the packing density varied between 57 and 64 %.

A good quantitative agreement between the numerical and experimental results was obtained for granular specimens of various size ratios and volume fractions of smaller particles; however, DEM provided samples with significantly smaller solid fractions.

3.2 Coordination number

In the three-dimensional monodisperse packing of frictionless spheres, the average coordination number (CN), is expected to be six, which is equal to twice the number of degrees of freedom per particle [35]. Monodisperse samples of uniform spheres and mixtures composed of particles with a small degree of polydispersity are arranged in a crystalline formation with a homogeneous distribution of contacts throughout the system [7]. Each particle in the sample is supported by several neighbouring particles and it supports other particles. In highly heterogeneous mixtures, where small spheres partially fill the pores between larger particles, each particle is supported by neighbouring particles but it does not necessarily support others. As these particles do not contribute to the force transmission through the system, a corrected coordination number (CN*) in which mechanically unstable particles with less than four contacts were excluded from calculations has been introduced by Göncü et al. [36]. Wiącek and Molenda [8] observed an increase in the corrected coordination number by 25 %, as compared to the classical coordination number, in assemblies with a high degree of polydispersity.

The evolutions of the classical average coordination numbers (CN) and the corrected coordination numbers (CN*) in numerical sphere packings with various size ratios and volume fractions of small particles are shown in Fig. 3. The coordination number varies with the distance from the wall due to the wall effect; therefore, the particles lying within three diameters of larger spheres from the walls of the chamber were excluded from calculation to reduce the wall effect. The average coordination number was slightly smaller in mixtures with the volume fraction of smaller components of 0.2, as compared to monodisperse samples of large spheres due to evolution of the packing structure from the ordered to the disordered one. The average coordination numbers in monodisperse assemblages were close to 6, which means that these samples reached mechanical stability and might be termed isostatic [5].

In mixtures with \(g=0.8\), composed of similarly sized particles, no impact of contribution of small spheres on CN value was observed. In mixtures with smaller particle size ratios, the number of contacts between spheres increased with the volume fraction of small particles increasing up to 0.6, which was followed by the decrease in the coordination number for higher f values. In these packings, the relationships between the average coordination number and the volume fraction of smaller spheres followed the similar paths to solid fraction-volume fraction curves.

Fig. 4
figure 4

The evolution of average coordination numbers for contacts between large particles (a), large and small particles (b), small and large particles (c) and small particles (d) with the volume fraction of small particles in mixtures with particle size ratios of 0.4 and 0.8

Full size image
Fig. 5
figure 5

Probability distribution for the number of contacts per particle in numerical samples with various size ratios and volume fractions of small spheres of \(f=0.2\) (a), \(f=0.8\) (b)

Full size image

As the average coordination number in the polydisperse granular packing is determined by contacts between different types of particles [37], the detailed analysis of the average coordination numbers for spheres representing respective fractions in assemblies was conducted in this study. Figure 4 shows the evolution of the average coordination numbers for contacts between spheres with the contribution of small particles in mixtures with various particle size ratios. The CN values for equally sized spheres were similar in the examined packings, contrary to the values of the parameter calculated for contacts between non-uniformly sized spheres. Coordination numbers for contacts between large and small particles were higher in samples with \(g=0.4\) and increased sharply with an increase in the number of small spheres. In turn, the CN values for contacts between small and large particles in these mixtures were smaller and decreased with increasing f value. These results indicate that the average coordination number in binary mixtures is determined mainly by contacts between large and small particles.

Figure 3b illustrates a change in the corrected coordination number with the increasing particle size ratio and the volume fraction of small spheres in binary mixtures. Values of the parameter strongly varied in samples with the volume fraction of small particles of 0.2 which resulted from differences in the population of particles with contacts smaller than 4 in packings with different g values (Fig. 5a). A slight influence of the size ratio on CN* value was observed for higher volume fractions of small components.

Figure 5 shows the probability distributions for the number of contacts per particle (N) in the binary samples with various size ratios and volume fractions of small beads of 0.2 and 0.8. No statistically significant difference was found in probability distributions for mixtures with g value of 0.8 and various volume fractions; however, a decrease in the particle size ratio resulted in the more heterogeneous distribution of contact numbers per particle in the packings with higher f values. The probability distributions for mixtures with size ratios of 0.6 and 0.8 were symmetrical, while the ones for higher \(g=0.4\) were asymmetrical and right-skewed.

The coordination number is a fundamental geometrical parameter dependent on the structure of granular assembly, therefore, numerous effort has been made to determine the relationship between the average number of contacts and parameters describing structural properties of packing. In 1980, Dodds [38] introduced the following formula for the coordination number in isotropic mixtures composed of uniformly sized homogeneous particles of types q and p

$$\begin{aligned} CN_{p,q} =f_q CN, \quad p,q=1,2 \end{aligned}$$
(7)

where \(f_q \) is a volume fraction of particles q and CN is an average coordination number.

As the coordination number was found to be determined by structural properties of granular assembly, Artz [39] expressed the coordination number as a function of the relative density of the particulate system (D); however, application of Artz was limited for the early stages of compaction. Thus, Helle et al. [40] has developed simple approximation, applicable for I and II stage of compaction under hydrostatic pressure:

$$\begin{aligned} CN=12D. \end{aligned}$$
(8)

Further studies on relationship between the coordination number and the solid fraction in sphere packings conducted by, inter alia, O’Hern et al. [41], Majmudar et al. [42] and Göncü et al. [36] have shown that CN exhibits a following power law:

$$\begin{aligned} CN-CN_c \propto \left( {\varphi -\varphi _c } \right) ^{\beta }, \end{aligned}$$
(9)

where critical value of solid fraction \(\varphi _{c}\) is the one for which there are enough contacts per particle \((CN_{c})\) to satisfy the conditions of mechanical stability and \(\beta \approx 0.5\) [42].

Many equations have been proposed over the last few decades to estimate the average coordination number of monodisperse granular packings [38–40]. A number of studies have also been conducted to derive a formula for nonuniformly sized granular systems [11, 36, 43]; however, they still have not provided reasonable approximations for binary mixtures.

It has already been shown that the average coordination number in polydisperse granular packing is determined by contacts between different types of particles [18, 44]. Turner and Ashby [37] proposed formulas for average coordination numbers between particles representing respective fractions. Average coordination numbers for contacts between large particles \((CN_{ll})\), large and small particles \((CN_{ls})\), small and large particles \((CN_{sl})\) and small particles \((CN_{ss})\) may be expressed as:

$$\begin{aligned} \begin{aligned} CN_{ll}&=\frac{1-k}{\left( {1-k+kg} \right) ^{2}}CN,\\ CN_{ls}&=\frac{kg}{\left( {1-k+kg} \right) ^{2}}CN,\\ CN_{sl}&=\frac{\left( {1-k} \right) g}{\left( {1-k+kg} \right) ^{2}}CN,\\ CN_{ss}&=\frac{kg^{2}}{\left( {1-k+kg} \right) ^{2}}CN, \end{aligned} \end{aligned}$$
(10)

where k is a number fraction of small particles and g is a ratio between the diameter of a small and large particle.

The numerical results and theoretical predictions of average coordination numbers from Eq. (10) for binary mixtures with particle the size ratio of 0.8 as a function of the volume fraction of smaller particles are shown in Fig. 6. Equation (10) were found to be highly accurate approximations to numerical results in samples with a high particle size ratio. The difference between numerical and theoretical predictions decreased with g value increasing, which was illustrated in Fig. 7. Skrinjar and Larsson [12] reported that the theoretical CN values calculated for contacts between large–small and small–large particles deviated from numerical results at high number fractions of small particles; however, in this study, no impact of contribution of small particles on accuracy of approximation of Eq. (10) to numerical data was observed.

As the Eq. (7), proposed by Dodds [38], defines the coordination number as a function of volume faction of particles of different types, the fits of Eq. (7) to the numerical data for large–large and small–small particles were included in Fig. 6 to verify the applicability of the formula for bidisperse granular packings with different volume fractions of small particles. Equation (7) was found to be a surprisingly good approximation of numerical CN values for contacts between large particles; however, it provided smaller coordination numbers for small particles, as compared to numerical results.

Fig. 6
figure 6

The coordination number for respective fractions of particles as a function of the volume fraction of small particles in mixtures with the size ratio of 0.8. The solid lines are the fits of Eq. (10), to the numerical data. The dashed lines are fits of Eq. (7) to the numerical data for large–large and small–small particles

Full size image
Fig. 7
figure 7

The coordination number for respective fractions of particles as a function of the size ratio in mixtures with the volume fraction of 0.4

Full size image
Fig. 8
figure 8

Radial distribution functions for small particles (a) and large particles (b) in numerical binary mixtures with various volume fractions of small particles and the size ratio of 0.8. Inset zoom into the peaks of the RDF at the distance between 1.4 and 3 particle diameters

Full size image
Fig. 9
figure 9

The organization of particles contributing to peaks in the radial distribution function for the two-dimensional monodisperse granular packing

Full size image
Fig. 10
figure 10

Radial distribution functions for small particles (a) and large particles (b) in numerical binary mixtures with various size ratios and the volume fraction of smaller particles of 0.8

Full size image

3.3 Radial distribution function

The composition of granular packing determines the arrangement of particles in an assembly affecting its geometrical properties. The spatial structure of the packing may be described by means of the RDF providing information about long range interparticle correlations and their organization [45]. The RDF g(r) may be expressed as [46]

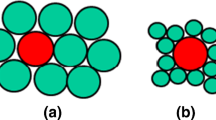
$$\begin{aligned} g\left( r \right) =\frac{n\left( r \right) }{4\pi r^{2}\Delta r\rho }, \end{aligned}$$
(11)

where n(r) is the number of the particles in a spherical shell occupying the space from a radial distance r to \(r + \Delta r\) from the center of the specified particle and \(\rho \) is the averaged density of particles, defined as a ratio between the number of particles and the volume of the assembly. In this study, \(\Delta r = 0.2D_{l}\). The g(r) is the probability distribution of finding the center of a particle in a given position at distance \(r + \Delta r\) from a reference one. The RDFs in packings with different volume fractions of smaller spheres and the size ratio of 0.8 for small and large particles were shown in Fig. 8. The RDFs were calculated for volumes of mixtures, appropriate for exclusion of the effect of the wall on the organization of spheres in the system. For monodisperse samples, the g(r) exhibited a sharp peak at \(r/D_{s}=1\) and smaller ones at the distance from the center of a reference particle equaled to 1.7, 2 and 2.6 particle diameters (inset of Fig. 8a), which corroborated findings reported previously by, inter alia Isola [4], Parafiniuk et al. [46] and Sain [47]. The distances of the second and the fourth peaks from the reference sphere are the multiple of \(\sqrt{3}\) reference sphere diameter. The presence of the peaks indicates an organized structure of the granular packing, presented in Fig. 9 for two-dimensional system. In the case of binary mixtures, the dominance of the structure of large particles over the smaller spheres in mixtures with the volume fraction smaller than 0.8 was observed, resulting in the second and third peaks at the distance from the reference small sphere equaled to 1.8 and 2.2 \(D_{s}\). The increase in f value to 0.8 in mixtures resulted in the RDF for small spheres similar to the one typical for the monodisperse sample. The RDFs for large particles, presented in Fig. 8b, exhibit second peak in distance from the reference large sphere decreasing with the increase in the contribution of small particles. For mixtures with the volume fraction of small particles higher than 0.4, the peak was observed at the distance equaled to 1.6 large particle diameters. The same effect was reported by Isola [4] who observed the dominance of the structure of small particles over the larger spheres in mixtures with number fraction of large particles of 30 and 50 % and the size ratio of 0.25 and 0.5. Although the peak at the distance from the reference sphere equaled to two large particle diameters was noticeable, the peaks at the distance equaled to the sum of the diameter of large and small particles were also apparent. The author observed that the increase in the contribution of large spheres into binary packings above 70 % decreased impact of small particles resulting in RDF close to the one typical for the monodisperse case. Isola found a strong influence of the volume fraction of large particles on the positon of peaks in the RDFs only for large particles, while, in this study, the RDF for both, large and small spheres differed significantly with the increasing contribution of large particles in the mixture. Moreover, the height of peaks increased with the decrease in the number of large particles in samples, indicating an increase in packing order.

Positions and heights of peaks in the RDFs were expected to be determined by particle sizes in binary packings. Figure 10 shows RDFs for small and large spheres for packings with different particle size ratios and volume fraction of small spheres of 0.8. For each sample, the g(r) for small particles exhibited a sharp peak at \(r/D_{s}=1\) and the second one at the distance from the center of the reference sphere between 1.7 and 2 particle diameters. The next peaks were apparent at the distance from the reference particle of 2.6, 2.9 and 3.5 sphere diameters and the height of peaks increased with the increasing particle size ratio. A much higher influence of the particle size ratio on the RDF was observed for large spheres (Fig. 10b), wherein positions and heights of peaks differed significantly.

4 Conclusions

The experimental and numerical investigations of randomly generated binary granular systems showed a strong influence of both, particle size ratio and contribution of small particles in packing on fundamental geometrical parameters of the sample. The size ratio was chosen not smaller than 0.4 to prevent small particles from percolating through bedding. The numerical results, provided by tests performed using DEM, were partially verified by the experimental results. The three-dimensional simulations have been carried out for assemblies of steel beads using EDEM software with simplified non-linear Hertz–Mindlin contact model. In mixtures with small to large particle size ratios higher that 0.7, the solid fraction was found to increase with the increasing volume fraction of small spheres. In packings with a higher difference between particles’ sizes, the solid fraction reached maximum when the volume fraction of smaller beads was 0.6. These results indicate the presence of the certain value of the particle size ratio above which the solid fraction of binary mixtures does not reach maximum. The results indicated a strong relationship between the coordination number and the solid fraction of binary mixtures. The average coordination number-volume fraction of smaller particles curves followed the similar paths to solid fraction-volume fraction of smaller particles curves. Coordination numbers for contacts between different types of particles varied significantly with the increasing contribution of small spheres in systems; however, CN value for all spheres was determined mainly by contacts between large and small particles. That effect was particularly apparent in samples with large differences between particles’ sizes. The numerical average coordination numbers for contacts between different types of particles in mixtures were compared to the theoretical predictions based on equations proposed earlier by Turner and Ashby [35] and Dodds [36]. While the formula introduced by Dodds was a good approximation of numerical CN values only for contacts between large particles, the equations of Turner and Ashby were accurate for all types of contacts. The accuracy of theoretical predictions increased with the increasing particle size ratio in assemblages; however, it was found not to be affected by the volume fraction of small spheres in beddings. The spatial structure of binary systems, described by means of the RDF, was also found to be strongly determined by both, the composition of packing and the degree of heterogeneity of particle sizes.

The combination of DEM computational modeling with experimental validation provided new scientific insight into the structural properties of bidisperse granular mixtures which leads to the improved analysis of their mechanical properties and more accurate interpretation or design of effects encountered in the industry.