The influence of particle rolling and imperfections on the formation of shear bands in granular material

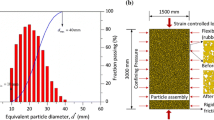
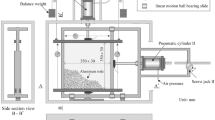
Abstract

This paper examines the development and evolution of shear bands in granular assemblies when particle rolling and imperfections are taken into account. Simulated biaxial tests in two-dimension are conducted using the discrete element method. The progressive development of rotational angles and effective strain are presented to describe the emergence and evolution of shear bands in biaxial tests. The simulated results reveal that when rolling resistance is taken into account in DEM, the development of shear bands is more distinct as the evolution of the minor shear bands is limited while the major shear bands are preferably promoted in granular materials, and that the local rotating bearings not only influence the onset of shear bands and the width of the shear bands, but also decrease the resistance and reduce the strength of the granular material. Also, it is demonstrated that the primary shear bands initiate from the imperfect areas and develop preferentially along the direction of imperfections. Therefore, the emergence and development of shear bands, which will result in a decline in strength and eventually lead to instability and destruction of the material, can be effectively simulated when rolling resistance is incorporated in DEM and the initial distribution of imperfections in the granular material is defined.

Appendix

The definition of effective strain for granular materials is briefly summarized.

To measure the change in position of a particle in relation to neighbouring particles, a nominal strain (i.e., the effective strain) is defined at the centre of the particle. Considering the change in position of particle A in relation to one of its neighbouring particles, denoted particle B and shown in Fig. 20, the nominal effective strain is defined as follows.

Fig. 20

The position of neighboring particles in different time

In Fig. 20, the relative change in position of two neighbouring particles at times $t_1$ and $t_2$ is considered. Using the XYZ global coordinate system, the centre coordinates of particles A and B are $\mathbf{X}_\mathrm{A}^\mathrm{1}$,$\mathbf{X}_\mathrm{B}^1$ at $t_1$ and $\mathbf{X}_\mathrm{A}^\mathrm{2}$, $\mathbf{X}_\mathrm{B}^2$ at $t_2$. The angles between the axis in the XYZ global coordinate system and the corresponding xyz local coordinate system are $\alpha _1$, $\beta _1$, $\gamma _1$ at $t_1$ and $\alpha _2$, $\beta _2$, $\gamma _2$ at $t_2$. The difference between the centre positions of particles A and B, using the global coordinate system, at $t_1$ and $t_2$ are

$$\begin{aligned} \Delta \mathbf{X}_{BA}^1 =\mathbf{X}_B^1 -\mathbf{X}_A^1 ; \quad \Delta \mathbf{X}_{BA}^2 =\mathbf{X}_B^2 -\mathbf{X}_A^2 \end{aligned}$$

(2)

The differences based on the local coordinate system can be expressed as

$$\begin{aligned} \Delta \mathbf{x}_{BA}^1 =\mathbf{x}_B^1 -\mathbf{x}_A^1 ; \quad \Delta \mathbf{x}_{BA}^2 =\mathbf{x}_B^2 -\mathbf{x}_A^2 \end{aligned}$$

(3)

The coordinate transformation result is

$$\begin{aligned} \Delta \mathbf{x}_{BA}^1 =\mathbf{T}_1 \Delta \mathbf{X}_{BA}^1 ; \quad \Delta \mathbf{x}_{BA}^2 =\mathbf{T}_2 \Delta \mathbf{X}_{BA}^2 \end{aligned}$$

(4)

where $\mathbf{T}_1$ and $\mathbf{T}_2$ are the coordinate transformation matrixes from the local coordinate system to the global coordinate system at $t_1$ and at $t_2$, respectively.

$$\begin{aligned}&\mathbf{T}_1 =\left[ {{\begin{array}{l@{\quad }l@{\quad }l} {\cos \gamma _1 }&{} {\sin \gamma _1}&{} 0 \\ {-\sin \gamma _1 }&{} {\cos \gamma _1}&{} 0 \\ 0&{} 0&{} 1 \\ \end{array} }} \right] \left[ {{\begin{array}{l@{\quad }l@{\quad }l} {\cos \beta _1}&{} 0&{} {-\sin \beta _1} \\ 0&{} 1&{} 0 \\ {\sin \beta _1}&{} 0&{} {\cos \beta _1} \\ \end{array} }} \right] \end{aligned}$$

(5)

$$\begin{aligned}&\mathbf{T}_2 =\left[ {{\begin{array}{l@{\quad }l@{\quad }l} {\cos \gamma _2}&{} {\sin \gamma _2}&{} 0 \\ {-\sin \gamma _2}&{} {\cos \gamma _2}&{} 0 \\ 0&{} 0&{} 1 \\ \end{array} }} \right] \left[ {{\begin{array}{l@{\quad }l@{\quad }l} {\cos \beta _2}&{} 0&{} {-\sin \beta _2} \\ 0&{} 1&{} 0 \\ {\sin \beta _2}&{} 0&{} {\cos \beta _2} \\ \end{array} }} \right] \end{aligned}$$

(6)

It means that by revolving $\beta _1$ around axis $y_1$, then $\gamma _1$ around axis $z_1$ at $t_1$, the local coordinate system can coincide with the global coordinate system. Similarly, by revolving $\beta _2$ around axis $y_2$, then $\gamma _2$ around axis $z_2$ at $t_2$, the local coordinate system can coincide with the global coordinate system.

As two-dimensional problem concerned, only the coordinate transformation within XY plane is considered [20]. The coordinate transformation matrixes are

$$\begin{aligned} \mathbf{T}_1 =\left[ {{\begin{array}{l@{\quad }l} {\cos \alpha _1 }&{} {\sin \alpha _1 } \\ {-\sin \alpha _1 }&{} {\cos \alpha _1 } \\ \end{array} }} \right] ; \quad \mathbf{T}_2 =\left[ {{\begin{array}{l@{\quad }l} {\cos \alpha _2 }&{} {\sin \alpha _2 } \\ {-\sin \alpha _2 }&{} {\cos \alpha _2 } \\ \end{array} }} \right] \end{aligned}$$

(7)

Deformation gradient f is used to describe the relative location change between particles A and B, from the material particle pair $A-B:\mathbf{X}_A^1 -\mathbf{X}_B^1$ at time $t_1$ , to the same material particle pair ${A}'-{B}':\mathbf{X}_A^2 -\mathbf{X}_B^2$ at time $t_2$ , referred to as $x_1 -y_1$, where f is defined as:

$$\begin{aligned} f=\frac{\Delta \mathbf{x}_{\mathrm{BA}}^2 }{\Delta \mathbf{x}_{\mathrm{BA}}^1 }=\mathbf{RU} \end{aligned}$$

(8)

In Eq. (8), $\mathbf{R}$ is the orthogonal tensor, which represents the rotation of the connecting line between particles A and B. $\mathbf{U}$ is a positive definite symmetric tensor, which represents the tensile deformation of the connecting line between particles A and B. They can be expressed as

$$\begin{aligned}&\mathbf{R}=\left[ {{\begin{array}{l@{\quad }l} {\cos \left( {\alpha _2 -\alpha _1 } \right) }&{} {-\sin \left( {\alpha _2 -\alpha _1 } \right) } \\ {\sin \left( {\alpha _2 -\alpha _1 } \right) }&{} {\cos \left( {\alpha _2 -\alpha _1 } \right) } \\ \end{array} }} \right] \end{aligned}$$

(9)

$$\begin{aligned}&\mathbf{U}=\left[ {{\begin{array}{ll} {\lambda _{\mathrm{AB}} }&{}\quad 0 \\ 0&{}\quad 1 \\ \end{array} }} \right] \end{aligned}$$

(10)

$$\begin{aligned}&\left\{ {{\begin{array}{l} {\lambda _{\mathrm{AB}} =\frac{l_{\mathrm{AB}}^2 }{l_{\mathrm{AB}}^1 }} \\ {l_{\mathrm{AB}}^\mathrm{1} =\left\| {\Delta \mathbf{x}_{\mathrm{BA}}^1 } \right\| } \\ {l_{\mathrm{AB}}^2 =\left\| {\Delta \mathbf{x}_{\mathrm{BA}}^2 } \right\| } \\ \end{array} }} \right. \end{aligned}$$

(11)

Equations (4), (7), and (8) result in

$$\begin{aligned} \left\{ {{\begin{array}{l} {\Delta \mathbf{X}_{\mathrm{BA}}^2 =\mathbf{F}\Delta \mathbf{X}_{\mathrm{BA}}^1 } \\ {\mathbf{F}=\mathbf{T}_2^\mathrm{T} \mathbf{fT}_1 } \\ \end{array} }} \right. \end{aligned}$$

(12)

According to the theory of continuum mechanics, the derivative tensor of the displacement gradient, defined by the relationship between the material coordinate and space coordinate, is

$$\begin{aligned} \mathbf{D}=\mathbf{F}-\mathbf{I} \end{aligned}$$

(13)

where $\mathbf{I}$ is the unit matrix. If $D_{ij}$ are the components of matrix $\mathbf{D}$, then

$$\begin{aligned}&\gamma _{\mathrm{AB}} =\left[ {\frac{2}{3}D_{ij} D_{ij} } \right] ^{1/2} \end{aligned}$$

(14)

$$\begin{aligned}&\gamma _\mathrm{e} =\frac{1}{n_A }\sum _{B=1}^{n_A } {\gamma _{AB} } \end{aligned}$$

(15)

where $\gamma _{\mathrm{AB}}$ is an intermediate variable, and $\gamma _\mathrm{e}$ is the effective strain at the centre of particle A, around which there are $n_\mathrm{A}$ neighbouring particles.